背景介绍
隐马尔可夫模型 (HMM) 是一种概率图模型。
我们知道,机器学习模型可以从频率派和贝叶斯派两个方向考虑,
- 频率派发展成形成了统计机器学习,核心是优化问题;
- model: 例如,超平面 f ( ω ) = ω T x + b f(\omega)=\omega^Tx+b f(ω)=ωTx+b 或者 回归(regression)等;
- strategy: 衡量模型好坏/评估准则 loss function;
- algorithm(求解):GD, SGD, 牛顿法, 拟牛顿法等。
- 贝叶斯派发展成了概率图模型,核心是推断问题(inference)或者求后验概率 p ( z ∣ x ) p(z|x) p(z∣x), 常常需要用MCMC方法进行积分。(注:通常 x x x表示数据)
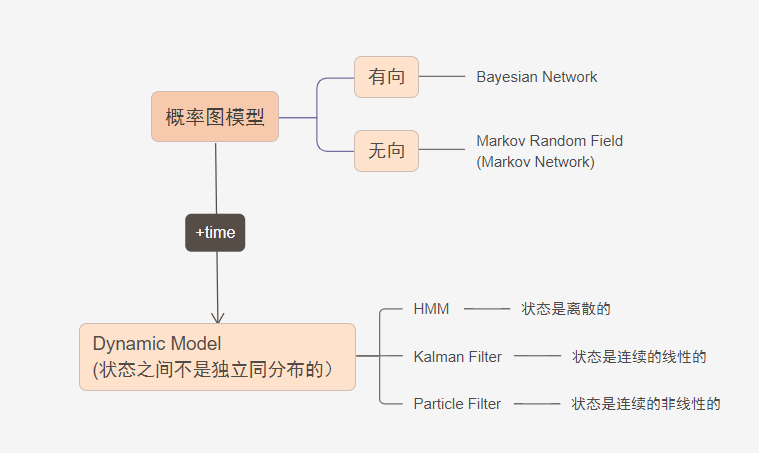
如图,概率图模型最基本的模型可以分为
- 有向图(贝叶斯网络 Bayesian Newwork)
- 无向图(马尔可夫随机场 Markov Random Field)
在这些基本的模型上,如果样本之间存在关联,可以认为样本中附带了时序信息(不一定是时间,是一个表示先后的量即可),从而样本之间不独立全同分布的,这种模型就叫做动态模型,隐变量随着时间发生变化,于是观测变量也发生变化。
根据状态变量(隐变量)的特点,可以分为:
- 隐马尔可夫模型(HMM),状态变量(隐变量)是离散的;
- 卡尔曼滤波(Kalman Filter),状态变量是连续的,线性的;
- 粒子滤波(Particle Filter),状态变量是连续,非线性的.
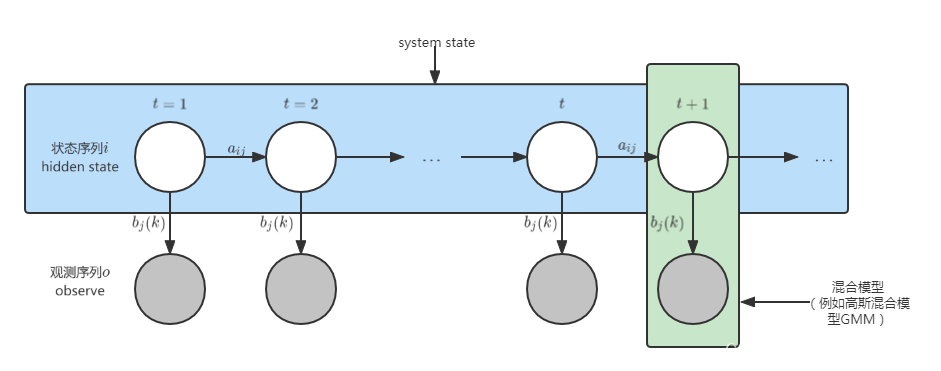
动态模型从横向看是一个时间序列,纵向看是一个混合模型:
提纲
下面的内容将分为以下三个部分进行叙述:
- 一个模型(隐马尔可夫模型)
- 两个假设
- 齐次马尔科夫假设
- 观测独立假设
- 三个问题
- Evaluation
- Learning
- Decoding
隐马尔可夫模型(HMM)
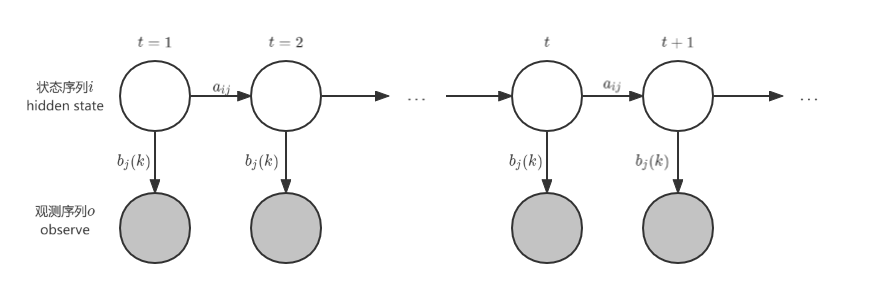
HMM 用概率图表示为:
符号表示
| 符号 | 解释 |
|---|---|
| λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B) | 一个表示模型的参数 |
| π \pi π | 初始时刻的概率分布 |
| A A A | 状态转移矩阵 |
| B B B | 发射矩阵,观测概率矩阵 |
更进一步:
- 观测变量:上图中灰色的圆圈表示观测变量,用符号 O : [ o 1 , o 2 , ⋯ , o t , ⋯ ] O: [o_1, o_2, \cdots , o_t, \cdots] O:[o1,o2,⋯,ot,⋯]表示,其值域为 V = { v 1 , v 2 , ⋯ , v M } V=\{v_1,v_2,\cdots,v_M\} V={ v1,v2,⋯,vM} ;
- 状态变量 Hidden state:上图中白色圆圈表示状态变量 Hidden state,用符号 i : [ i 1 , i 2 , ⋯ , i t , ⋯ ] i: [i_1, i_2, \cdots , i_t, \cdots] i:[i1,i2,⋯,it,⋯] 表示,其值域为 Q = { q 1 , q 2 , ⋯ , q N } Q=\{q_1,q_2,\cdots,q_N\} Q={ q1,q2,⋯,qN};
- 状态转移矩阵: A = [ a i j ] A=[a_{ij}] A=[aij],其中 a i j = p ( i t + 1 = q j ∣ i t = q i ) a_{ij}=p(i_{t+1}=q_j|i_t=q_i) aij=p(it+1=qj∣it=qi);
- 发射矩阵/观测概率矩阵: B = [ b j ( k ) ] B=[b_j(k)] B=[bj(k)] ,其中 b j ( k ) = p ( o t = v k ∣ i t = q j ) b_j(k)=p(o_t=v_k|i_t=q_j) bj(k)=p(ot=vk∣it=qj).
两个假设
在 HMM 中,有两个基本假设:
-
齐次 Markov假设(当前状态仅与前一状态有关):
p ( i t + 1 ∣ i t , i t − 1 , ⋯ , i 1 , o t , o t − 1 , ⋯ , o 1 ) = p ( i t + 1 ∣ i t ) (1) p(i_{t+1}|i_t,i_{t-1},\cdots,i_1,o_t,o_{t-1},\cdots,o_1)=p(i_{t+1}|i_t) \tag{1} p(it+1∣it,it−1,⋯,i1,ot,ot−1,⋯,o1)=p(it+1∣it)(1) -
观测独立假设(当前的观测变量只与当前的状态变量有关):
p ( o t ∣ i t , i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = p ( o t ∣ i t ) (2) p(o_t|i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1)=p(o_t|i_t) \tag{2} p(ot∣it,it−1,⋯,i1,ot−1,⋯,o1)=p(ot∣it)(2)
三个问题:
- Evaluation:
在所有参数 λ \lambda λ已知的条件下,观测序列的概率,即 p ( O ∣ λ ) p(O|\lambda) p(O∣λ);
通常采用前向后向算法(Forward-Backward Algorithm)解决。 - Learning:
如何求 λ \lambda λ? 即如何求 λ = a r g m a x λ p ( O ∣ λ ) \lambda=\mathop{argmax}\limits_{\lambda}p(O|\lambda) λ=λargmaxp(O∣λ)?
通常采用EM 算法(即Baum-Welch算法,Baum-Welch算法在EM前提出,后来发现它本质就是EM算法)。 - Decoding:
找到一个系列 I I I使 p ( I ∣ O , λ ) p(I|O,\lambda) p(I∣O,λ)最大,即 I = a r g m a x I p ( I ∣ O , λ ) I=\mathop{argmax}\limits_{I}p(I|O,\lambda) I=Iargmaxp(I∣O,λ)最大;
通常使用Vierbi 算法;
同时这类问题还可以分成两个小问题- 预测问题: p ( i t + 1 ∣ o 1 , o 2 , ⋯ , o t ) p(i_{t+1}|o_1,o_2,\cdots,o_t) p(it+1∣o1,o2,⋯,ot)<