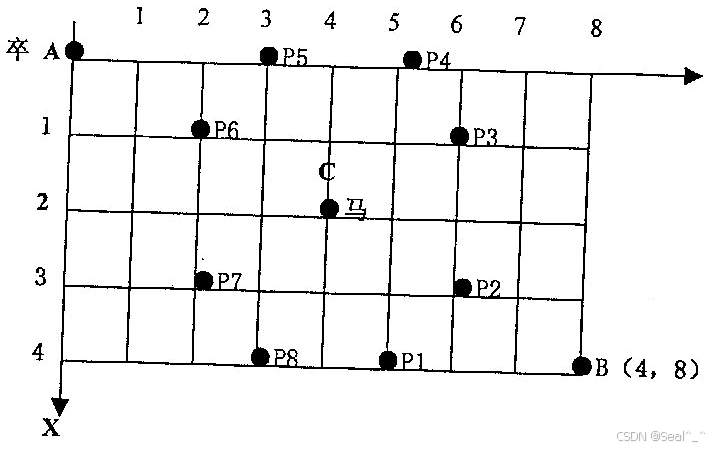
如图，A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点（图中的P1，P2 … P8 和 C）。卒不能通过对方马的控制点。

棋盘用坐标表示，A 点（0，0）、B 点（n,m）(n,m 为不超过 20 的整数，并由键盘输入)，同样马的位置坐标是需要给出的（约定: C<>A，同时C<>B）。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数。

输入

一行四个数据，分别表示B点坐标和马的坐标。

输出

一个数据，表示所有的路径条数。

样例输入

6 6 3 2

样例输出

17

C 语言实现的代码：

#include <stdio.h>

// 定义最大棋盘尺寸
#define MAX_SIZE 30

// 马的移动坐标变化量
int horseXSteps[] = {-2, -2, -1, -1, 1, 1, 2, 2};
int horseYSteps[] = {1, -1, 2, -2, 2, -2, 1, -1};

int main() {
    int n, m, x, y;
    // 输入终点位置和马的位置
    scanf("%d %d %d %d", &n, &m, &x, &y);
    n += 1; // 整体空出一行一列，便于边界检查
    m += 1;
    x += 1;
    y += 1;
    long long dp[MAX_SIZE][MAX_SIZE] = {0};
    dp[1][0] = 1;
    // 标记马能一步跳到的位置为不可达（值为 -1）
    for (int i = 0; i < 8; i++) {
        int newX = x + horseXSteps[i];
        int newY = y + horseYSteps[i];
        if (newX >= 1 && newX <= n && newY >= 1 && newY <= m) {
            dp[newX][newY] = -1;
        }
    }
    // 马所在的位置也不能走，标记为 -1
    dp[x][y] = -1;
    // 遍历所有的行和列，计算路径条数
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (dp[i][j] == -1) {
                dp[i][j] = 0;
            } else {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    // 输出从起点到终点的路径条数
    printf("%lld\n", dp[n][m]);
    return 0;
}

C++实现的代码：

#include <iostream>

// 定义最大棋盘尺寸
const int MAX_SIZE = 30;

// 马的移动坐标变化量
int horseXSteps[] = {-2, -2, -1, -1, 1, 1, 2, 2};
int horseYSteps[] = {1, -1, 2, -2, 2, -2, 1, -1};

int main() {
    int n, m, x, y;
    // 输入终点位置和马的位置
    std::cin >> n >> m >> x >> y;
    n += 1; // 整体空出一行一列，便于边界检查
    m += 1;
    x += 1;
    y += 1;
    long long dp[MAX_SIZE][MAX_SIZE] = {0};
    dp[1][0] = 1;
    // 标记马能一步跳到的位置为不可达（值为 -1）
    for (int i = 0; i < 8; i++) {
        int newX = x + horseXSteps[i];
        int newY = y + horseYSteps[i];
        if (newX >= 1 && newX <= n && newY >= 1 && newY <= m) {
            dp[newX][newY] = -1;
        }
    }
    // 马所在的位置也不能走，标记为 -1
    dp[x][y] = -1;
    // 遍历所有的行和列，计算路径条数
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (dp[i][j] == -1) {
                dp[i][j] = 0;
            } else {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    // 输出从起点到终点的路径条数
    std::cout << dp[n][m] << std::endl;
    return 0;
}

Java 实现的代码：

import java.util.Scanner;

class PathCounting {
    // 定义最大棋盘尺寸
    static final int MAX_SIZE = 30;

    // 马的移动坐标变化量
    static int[] horseXSteps = {-2, -2, -1, -1, 1, 1, 2, 2};
    static int[] horseYSteps = {1, -1, 2, -2, 2, -2, 1, -1};

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n, m, x, y;
        // 输入终点位置和马的位置
        n = scanner.nextInt();
        m = scanner.nextInt();
        x = scanner.nextInt();
        y = scanner.nextInt();
        n += 1; // 整体空出一行一列，便于边界检查
        m += 1;
        x += 1;
        y += 1;
        long[][] dp = new long[MAX_SIZE][MAX_SIZE];
        dp[1][0] = 1;
        // 标记马能一步跳到的位置为不可达（值为 -1）
        for (int i = 0; i < 8; i++) {
            int newX = x + horseXSteps[i];
            int newY = y + horseYSteps[i];
            if (newX >= 1 && newX <= n && newY >= 1 && newY <= m) {
                dp[newX][newY] = -1;
            }
        }
        // 马所在的位置也不能走，标记为 -1
        dp[x][y] = -1;
        // 遍历所有的行和列，计算路径条数
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (dp[i][j] == -1) {
                    dp[i][j] = 0;
                } else {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        // 输出从起点到终点的路径条数
        System.out.println(dp[n][m]);
    }
}

Python 实现的代码：

# 定义最大棋盘尺寸
MAX_SIZE = 30

# 马的移动坐标变化量
horseXSteps = [-2, -2, -1, -1, 1, 1, 2, 2]
horseYSteps = [1, -1, 2, -2, 2, -2, 1, -1]

n, m, x, y = map(int, input().split())
n += 1
m += 1
x += 1
y += 1
dp = [[0] * MAX_SIZE for _ in range(MAX_SIZE)]
dp[1][0] = 1
# 标记马能一步跳到的位置为不可达（值为 -1）
for i in range(8):
    newX = x + horseXSteps[i]
    newY = y + horseYSteps[i]
    if newX >= 1 and newX <= n and newY >= 1 and newY <= m:
        dp[newX][newY] = -1
# 马所在的位置也不能走，标记为 -1
dp[x][y] = -1
# 遍历所有的行和列，计算路径条数
for i in range(1, n + 1):
    for j in range(1, m + 1):
        if dp[i][j] == -1:
            dp[i][j] = 0
        else:
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
# 输出从起点到终点的路径条数
print(dp[n][m])