目录
下面是关于PointNet原理的相关证明及理解,这里主要是用PPT做的证明笔记。
一、置换不变性
首先需要知道什么是置换不变性:
设计的网络必须满足置换不变性,N个数据就有N!个置换不变性。而对称函数可以满足上述置换不变性。直接对数据做对称性操作,虽然满足置换不变性,容易丢失很多的几何和有意义的信息。比如取最大值时,只取得最远点,取平均值,只取得重心。
更多有关置换不变性的内容可以看其他笔记。
如果对点云数据及其挑战不是很清楚,建议先看【点云数据理解(PointNet实现第3步)】
二、定理1的证明
定理1:证明了PointNet网络可以拟合到任意的连续集合函数,只要是该函数是在hausdorff空间是连续的,那么就可以通过增加神经网络的深度以及宽度,来对这个函数进行逼近。
下面是定理1的证明:
下图笔者我给了一个示例帮助大家来理解。
在理解定理1的同时,我们还需要知道什么是指示函数:
指示函数(indicator function):是用来标注一个点是否属于集合,如果属于值为1,反之值为0。
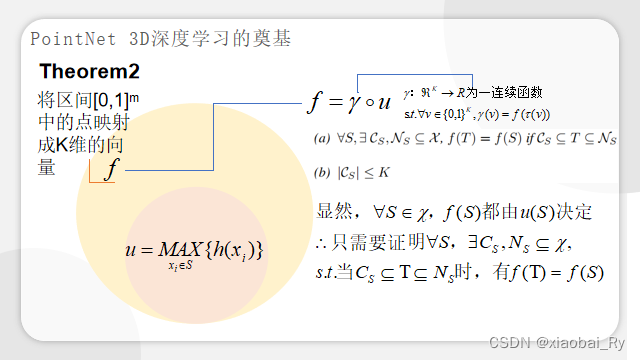
三、定理2的证明
定理2:对于任何输入都存在关键集和最大集,使得对和之间的任何集合,其网络输出都一样。
即对噪声和数据损坏都有鲁棒性。
- 定理2(a)说明对于任何输入数据集,都存在一个关键集和一个最大集,使得对和之间的任何集合,其网络输出都和一样。
- 定理2(b)说明了关键集的数据多少由maxpooling操作输出数据的维度K给出上界。
下面是定理2的证明:
下面笔者同样给出了一个示例来帮助大家理解:
对于任何输入数据集S,都存在一个最小集Cs和一个最大集Ns,使得对Cs和Ns之间的任何集合T,其网络输出都和S一样。由此,模型对输入数据在有噪声(引入额外的数据点,趋于Ns)和有数据损坏(缺少数据点,趋于Cs)的情况都是鲁棒的。
这里是论文中相关的实验验证:
下面是有关这份PPT的全部概览:
以下就是全部PPT的内容了:
这里笔者附上下载链接,有需要自行下载即可:【PointNet原理证明PPT】
四、简短介绍
3D深度学习的初步探索(PointNet,PointNet++,Geo-CNN论文理解)
下面的PPT及演示是之前课程作业做的,时间已经有些久远(2020年),主要是PointNet,PointNet++,Geo-CNN论文相关要点的介绍。PPT设置的是自动播放模式,对应汇报的语言是调用科大讯飞的机器人语音API。时长大概在11分钟左右。PPT现在回头看太过花哨😔.....,不过不介意产品形式汇报😂,想要迅速了解可以看一下下面的PPT演示视频。
下面是PPT的概览
下面是PointNet,PointNet++,Geo-CNN论文PPT自动演示的视频:
PointNet,PointNet++,Geo-CNN
对应上面展示图像的演示视频。下面是相关的参考文献:
[1]【3D计算机视觉】从PointNet到PointNet++理论及pytorch代码_小执着的博客-CSDN博客_pointnet
[2]论文笔记:Geo-CNN_hongbin_xu的博客-CSDN博客_modeling local geometric structure of 3d point clo
https://blog.csdn.net/hongbin_xu/article/details/87473876
[3]CVPR 2019 | 旷视研究院提出Geo-CNN:建模3D点云的局部几何结构
[4]斯坦福大学在读博士生祁芮中台:点云上的深度学习及其在三维场景理解中的应用
[5]【论文翻译】从零开始PointNet论文分析与代码复现_BatFlo_wsh的杂货铺-CSDN博客_pointnet复现
https://blog.csdn.net/BatFlo_wsh/article/details/89330195
对于上面的各网络的理解:
- 有关PointNet的理解可以看【PointNet理解(PointNet实现第4步)】
- 有关PointNet++的理解【有关PointNet++的理解】