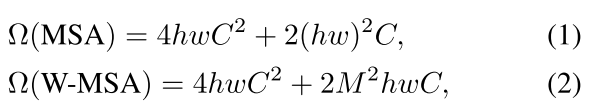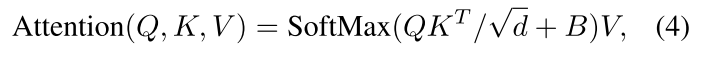论文: 《Swin Transformer: Hierarchical Vision Transformer using Shifted Windows》
代码: https://github.com/microsoft/Swin-Transformer
创新点
Transformer从语言应用到视觉,主要有两大挑战:
1、图像中目标尺寸变化大;
2、与文本中单词量相比,图像中像素数量更大;
为了解决这些差异,我们提出了一种分层Transformer,其特征是用 Shifted windows 计算的。移位窗口方案通过将 self-attention 计算限制在不重叠的本地窗口上,同时还允许跨窗口连接,从而带来更高的效率;与图像大小相关的的线性复杂度;
性能:
在分类任务ImageNet-1k上,top1 accuracy达到87.3%;在COCO test数据集上检测性能达到58.7AP,分割性能51.1AP;
算法
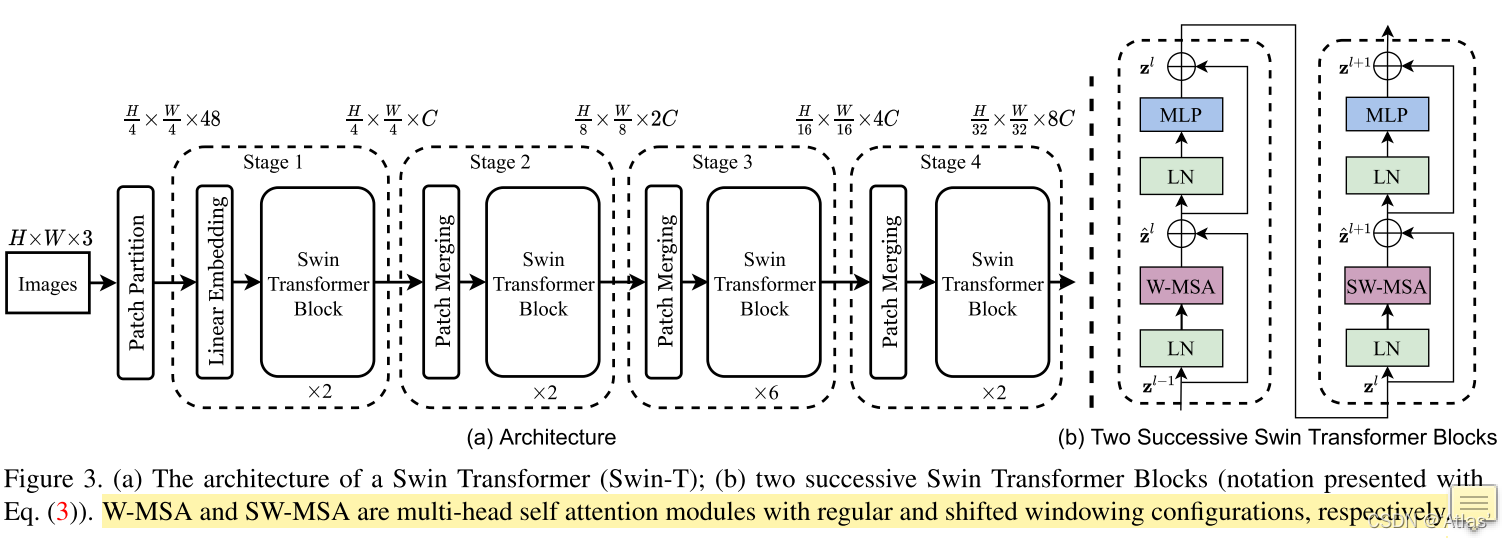
Swin Transformer结构如图3a所示,
Swin Transformer流程如下:
1、输入
(
N
,
3
,
224
,
224
)
(N, 3, 224, 224)
(N,3,224,224)图像,经过Patch Partition以及Linear Embedding输出为
(
N
,
96
,
56
∗
56
)
(N, 96, 56*56)
(N,96,56∗56),此处C=96,(该过程通过kernal为patch size=4卷积实现);
2、进入stage1,Swin Transformer Block结构如图3b,主要包括输入W-MSA及SW-MSA。首先进行进行归一化,window partition,window size=7,输出为维度为
(
64
N
,
7
,
7
,
96
)
(64N,7,7,96)
(64N,7,7,96);该结果经过attention模块(W-MSA)+FFN;(64个window)(MSA结构可以参考之前文章Transformer结构解读)
3、上述输出经过归一化,x进行偏移window size//2大小,而后进行window partition,window size=7,以及attention模块(SW-MSA)+FFN;
4、上述输出经过patch merging降低分辨率;进入stage2阶段,以此类推;
Patch Merging
为了生成多级分辨率,随着网络加深,通过Patch Merging层实现;
第一个Patch Merging,stage2阶段,对于
(
C
,
W
/
4
,
H
/
4
)
(C,W/4,H/4)
(C,W/4,H/4)的输入,将2*2个patch归为一组,channel 变为4C,分辨率变为之前1/4,输出为
(
4
C
,
W
/
8
,
H
/
8
)
(4C,W/8,H/8)
(4C,W/8,H/8),其过程类似feat reshape操作;而后降维为2C输出
(
2
C
,
W
/
8
,
H
/
8
)
(2C,W/8,H/8)
(2C,W/8,H/8);
stage3、stage4输出分辨率分别为
(
4
C
,
W
/
16
,
H
/
16
)
,
(
8
C
,
W
/
32
,
H
/
32
)
(4C,W/16,H/16),(8C,W/32,H/32)
(4C,W/16,H/16),(8C,W/32,H/32).
W-MSA
全局self-attention计算成本高,使用window based self-attendtion可降低计算量。如式1为全局attention,式2为使用窗口attention计算复杂度;
self-attention的计算瓶颈在于全图匹配QK,改为窗口内,可大大降低计算量,如式2。
式1,MSA计算复杂度分析如下,
1、MSA生成三个特征向量Q,K,V过成:
Q
=
x
∗
W
Q
,
K
=
x
∗
W
K
,
V
=
x
∗
W
V
Q=x*W^Q,K=x*W^K,V=x*W^V
Q=x∗WQ,K=x∗WK,V=x∗WV 。x的维度是
(
h
w
,
C
)
(hw,C)
(hw,C),W的维度是
(
C
,
C
)
(C,C)
(C,C),那么这三项的计算复杂度是
3
h
w
C
2
3hwC^2
3hwC2;
2、Attention中计算
Q
K
T
QK^T
QKT:Q,K,V的维度是
(
h
w
,
C
)
(hw,C)
(hw,C) ,因此该过程的复杂度是
(
h
w
)
2
C
(hw)^2C
(hw)2C
3、Softmax之后乘V得到Z:因为
Q
K
T
QK^T
QKT的维度是
(
h
w
,
h
w
)
(hw,hw)
(hw,hw),所以该过程的复杂度是
(
h
w
)
2
C
(hw)^2C
(hw)2C;
4、
Z
Z
Z乘矩阵
W
Z
W^Z
WZ得到最终输出:它的复杂度是
h
w
C
2
hwC^2
hwC2
因此MSA计算复杂度为
4
h
w
C
2
+
2
(
h
w
)
2
C
4hwC^2+2(hw)^2C
4hwC2+2(hw)2C。
式2,W-MSA计算复杂度分析如下,每个window有
M
∗
M
M*M
M∗M个Patch,
1、计算复杂度为,
3
∗
(
h
/
M
)
∗
(
w
/
M
)
∗
M
2
∗
C
2
=
3
h
w
C
2
3*(h/M)*(w/M)*M^2*C^2=3hwC^2
3∗(h/M)∗(w/M)∗M2∗C2=3hwC2;
2、计算复杂度为,
(
h
/
M
)
∗
(
w
/
M
)
∗
(
M
2
)
∗
(
M
2
)
∗
C
=
h
w
M
2
C
(h/M)*(w/M)*(M^2)*(M^2)*C=hwM^2C
(h/M)∗(w/M)∗(M2)∗(M2)∗C=hwM2C
3、计算复杂度为,
(
h
/
M
)
∗
(
w
/
M
)
∗
(
M
2
)
∗
(
M
2
)
∗
C
=
h
w
M
2
C
(h/M)*(w/M)*(M^2)*(M^2)*C=hwM^2C
(h/M)∗(w/M)∗(M2)∗(M2)∗C=hwM2C
4、计算复杂度为,
(
h
/
M
)
∗
(
w
/
M
)
∗
M
2
C
2
=
h
w
C
2
(h/M)*(w/M)*M^2C^2=hwC^2
(h/M)∗(w/M)∗M2C2=hwC2
因此W-MSA计算复杂度为
3
h
w
C
2
+
2
M
2
h
w
C
3hwC^2+2M^2hwC
3hwC2+2M2hwC
SW-MSA
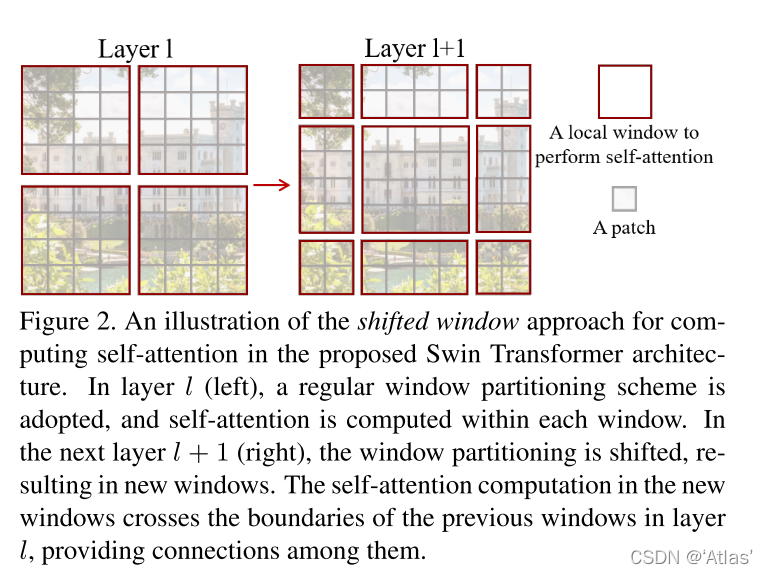
固定窗口缺少窗口之间联系,限制模型表达能力。为此引入shifted window partition方法,如图2所示;
layer l使用均匀窗口分割(W-MSA),layer l+1使用shifted 窗口分割(SW-MSA),生成窗口穿过layer l窗口的边界。
使用shifted window partition将生成更多窗口,并且个别窗口比较小,如图2右侧红色窗口;
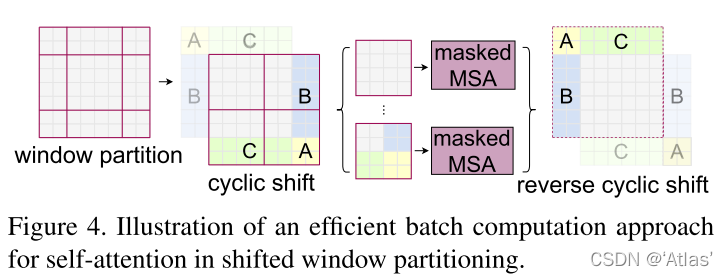
因此作者使用cyclic-shift,与常规窗口分割相比,窗口数量相等;如图4所示
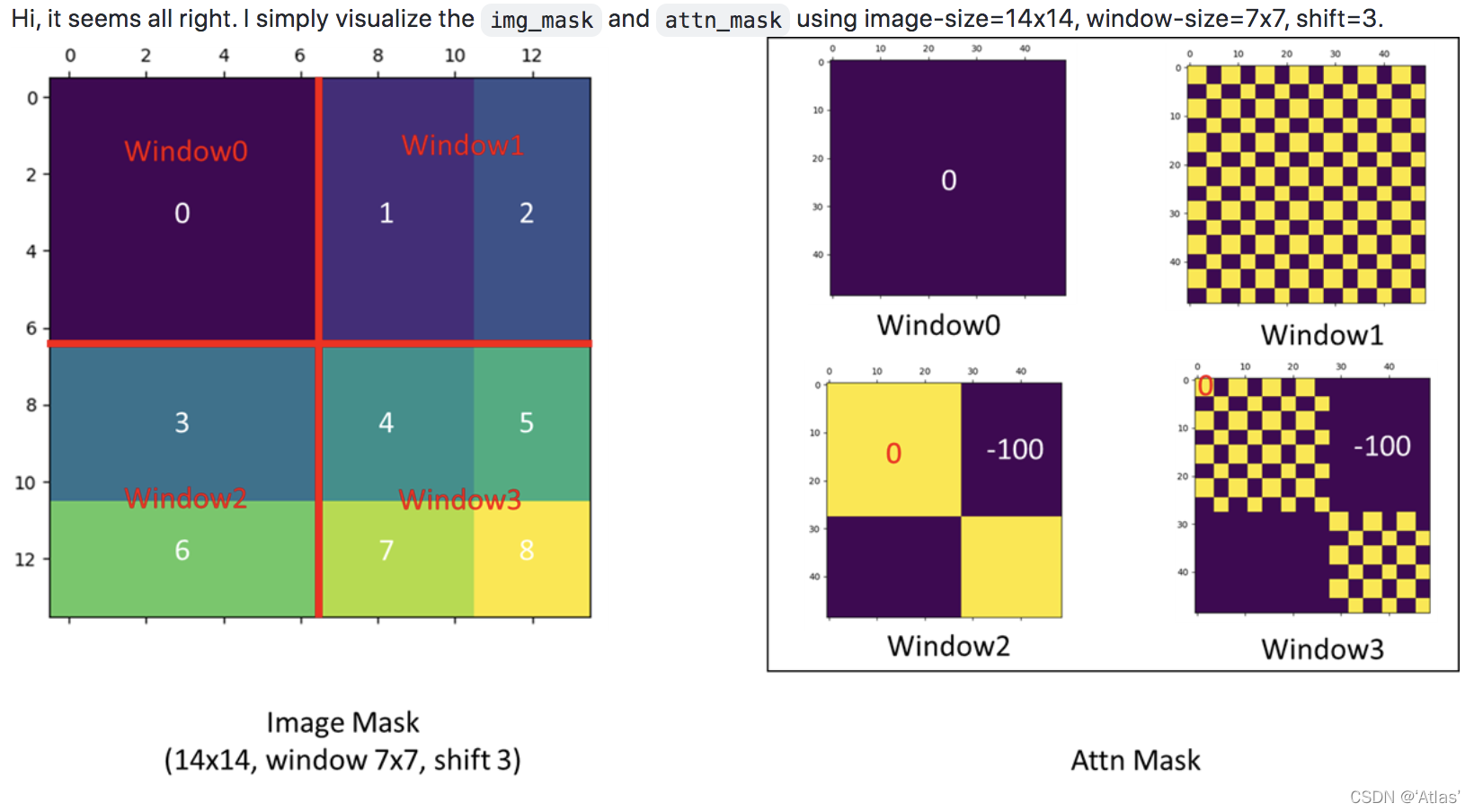
但是如图4所示,经过shift后一些在特征图中本不相邻区域,出现在同一窗口,这些区域之间不应进行attention计算,因此作者引入mask机制;
如下图所示,源自issue38
左图为原图经过偏移后结果,以window1举例,QKV为区域1和区域2穿插,但区域1与区域2不想计算attention,区域2由左侧shift而来,因此对应attn_mask如右上角,0与-100如棋盘状穿插,attn_mask加入softmax计算,-100对应结果趋近于0,起到mask作用。
位置偏置
作者在计算Attention过程中增加位置相关偏置项,如式4,
结构变体
Swin结构变体包括以下几种:
Window大小默认M=7,MSA中每个head的序列维度d=32,C表示stage1中隐藏层channel数;layer numbers表示每个stage层数
实验
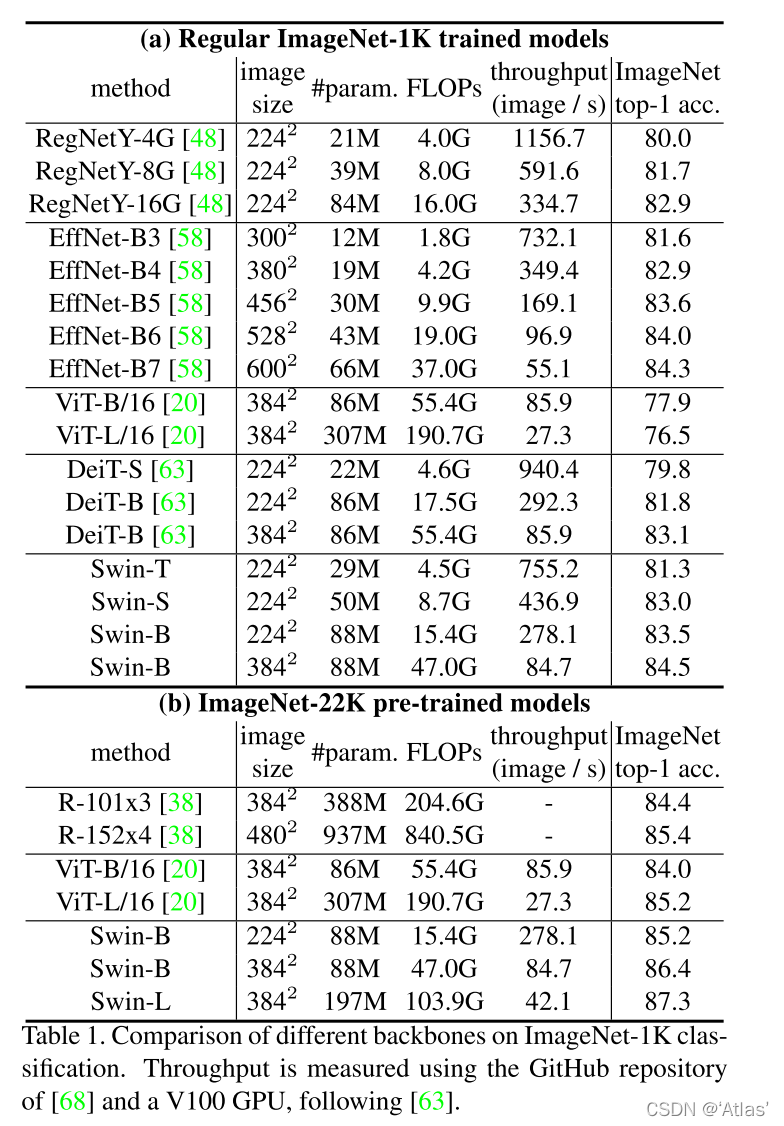
ImageNet分类
在ImageNet-1K数据上分类性能及计算量比较如表1所示,
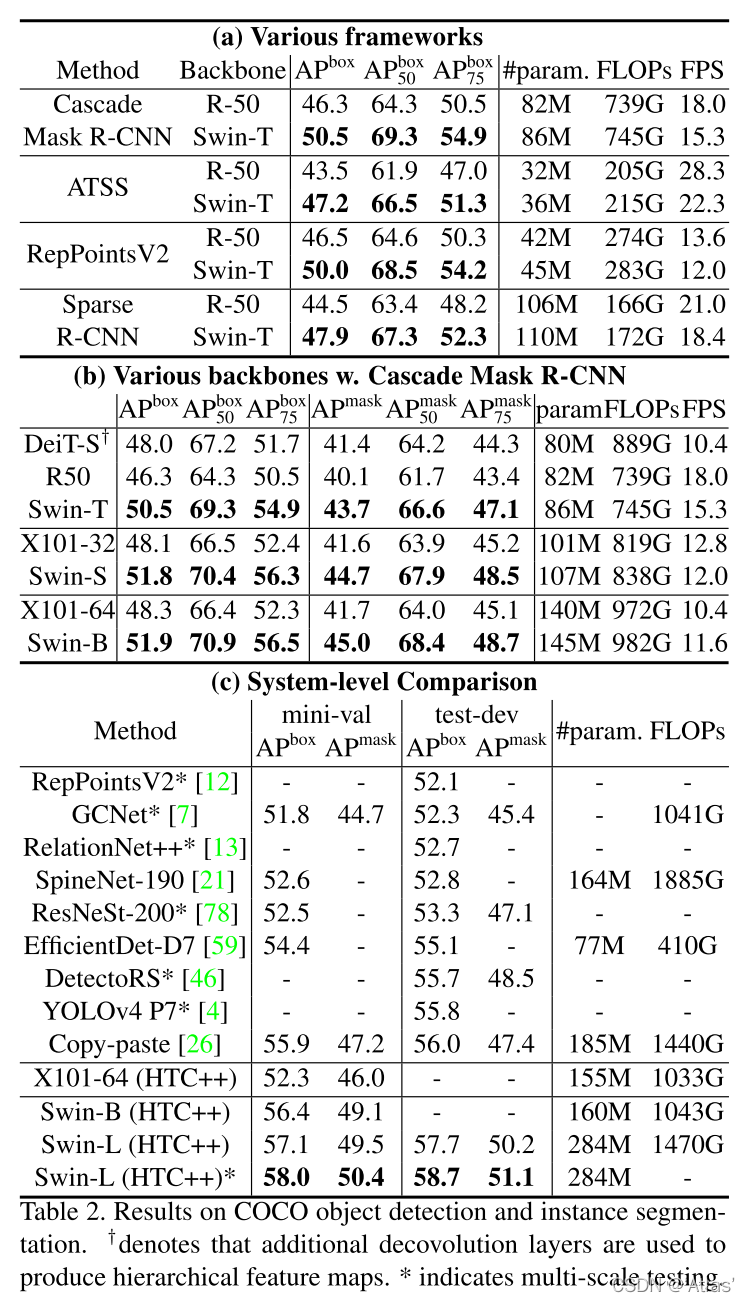
COCO目标检测
图2a作者比较Swin-T与ResNet50在四个检测框架下性能;
图2b作者使用Cascade Mask R-CNN检测框架,比较不同模型容量的Swin Transformer与ResNe(X)t性能;在相似参数量、计算量、FPS下Swin Transformer均取得不错性能;
图2c最好结果与之前SOTA进行对比;
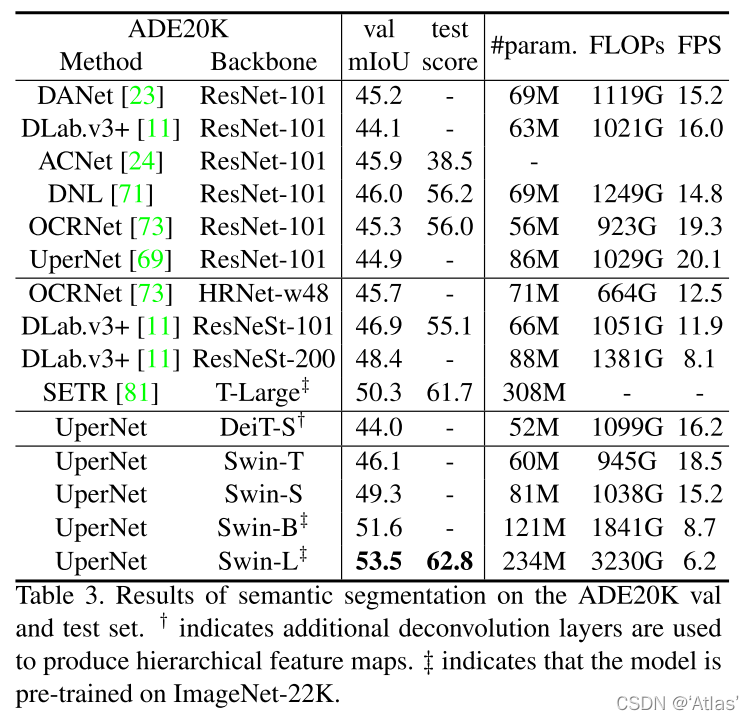
ADE20K语义分割
如表3
消融实验
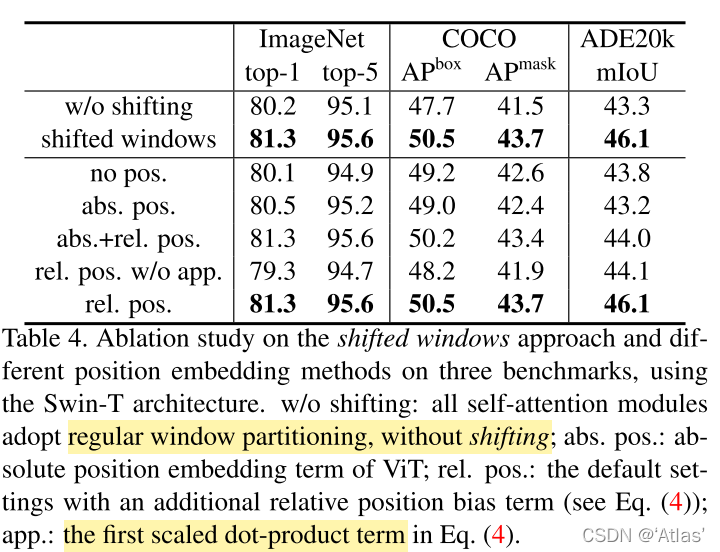
如表4,在分类、检测、分割任务上,作者进行如下比较试验;
- 是否使用shift window,结果表明shift window性能优于固定窗口;
- 不同位置编码方式比较实验,不使用位置编码、ViT中绝对位置编码、式4中增加位置相关偏置项,结果表明增加位置相关偏置项性能提升;式4中去掉
√
d
\surd d
√d项,性能下降;
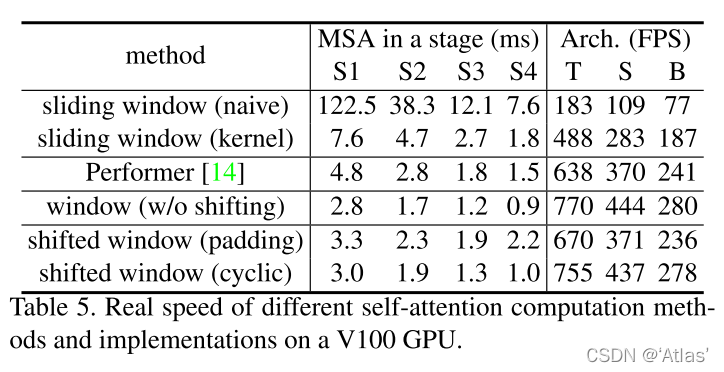
作者比较不同attention方法,耗时情况,如表5
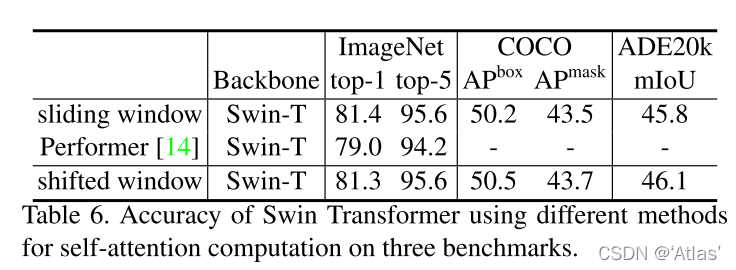
Swin Transformer略快于Performer,同时性能优于Performer,如表6,
结论
作者提出一种视觉Transformer,Swin Trnsformer,通过W-MSA及SW-MSA降低计算复杂度,生成多层级特征,证明SW-MSA有效性;在COCO目标检测及ADE20K语义分割任务上均取得SOTA性能;