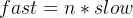LeetCode刷题|142题数学推导

关于这道题在官网已经有很详细的解法了，这里想对双指针法中为什么快指针取慢指针2倍步数做一个数学推导。

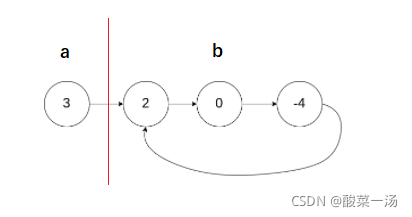
我们假设链表有环，那我们使用快指针和慢指针的方法，快指针就一定会追上慢指针。而且通过观察可以发现指针在当前链表中的路径有明显特点，那就是指针在进入环之后一直在环内循环。

我们假设非环部分有aa个节点，而环内有bb个节点，可以总结指针所经过的路径ss的几个特殊点：

当s=a-1s=a−1时，指针处于环外最后一个节点
当s=as=a时，指针第一次经过环的入点
当s=a+b-1s=a+b−1时，指针第一次走完了链表
当s=a+bs=a+b时，指针第二次经过环的入点
...
当s=a+kbs=a+kb时，指针第k+1k+1次经过环的入点

根据上述特点，我们可知，要想双指针在环的入点相遇，则必须使得两指针走过的路径长度满足a+nba+nb的关系式，为了计算方便，我们假设慢指针每次走一步，即当慢指针走过a+kba+kb步时与快指针相遇，则该位置便是我们要求的入点。

假设快指针步数为：

fast = n*slow

则两指针走过的路程应当满足：

$fast = slow + mb$

其中m为正整数，上式表达的含义是当快指针追上慢指针时快指针走过的总路程比慢指针走过的总路程多mb，即绕环m次后与慢指针相遇，大家可以类比绕操场跑步时的套圈超越。联立上面两个式子，得到

$n*slow = slow+mb$

整理可得

$slow = \frac{m}{n-1}b$

我们已知当 $slow=a+kb$ 时，慢指针应当在环的入点处，观察上式，当b的系数 $\frac{m}{n-1}$

为整数时，在其之上再加a步，即可构造slow=a+kbslow=a+kb的形式。因此我们需要解决如下两个问题：

找到满足 $\frac{m}{n-1}$ 的整数 n
在a未知的情况下如何让slow指针准确的走a步

第一个问题中m为一个正整数，因此只要能消掉分母中的n-1即可，最简单的方法便是令n=2。

解决第二个问题前我们再回顾一次链表的结构，我们将链表分成了环（a个节点）和非环（b个节点）两个部分，说到这里应该已经看明白了吧，慢指针需要向前走a个节点，那么此时我们再设一个辅助指针，让它从开头走到环的入点时，该指针走过的路程恰好是aa，而慢指针再前进a步也经过入点，因此两指针相遇的点便是我们最终求的所谓环的入点。

class Solution(object):
    def detectCycle(self, head):
        """
        :type head: ListNode
        :rtype: ListNode
        """
        slow, fast = head, head
        while True:
            if fast==None or fast.next==None:
                return None
            fast = fast.next.next
            slow = slow.next
            if fast == slow:
                break
        tmp = head
        while tmp!=slow:
            tmp = tmp.next
            slow = slow.next
        return tmp

LeetCode刷题|142题数学推导

悦读