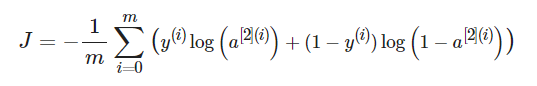目录
Q6. W,b的计算公式(Ng视频内容显示本就不全,非截图不全)
Q1.为什么使用要使用神经网络?
1.当面临输入数据集不是线性可分时,logistic回归模型表现不是很好。可以利用单隐藏层和神经网络来进行训练
2.数据集或特征很大时,神经网络的处理起来比较轻松
Q2.接下来的这个神经网络有什么特点?
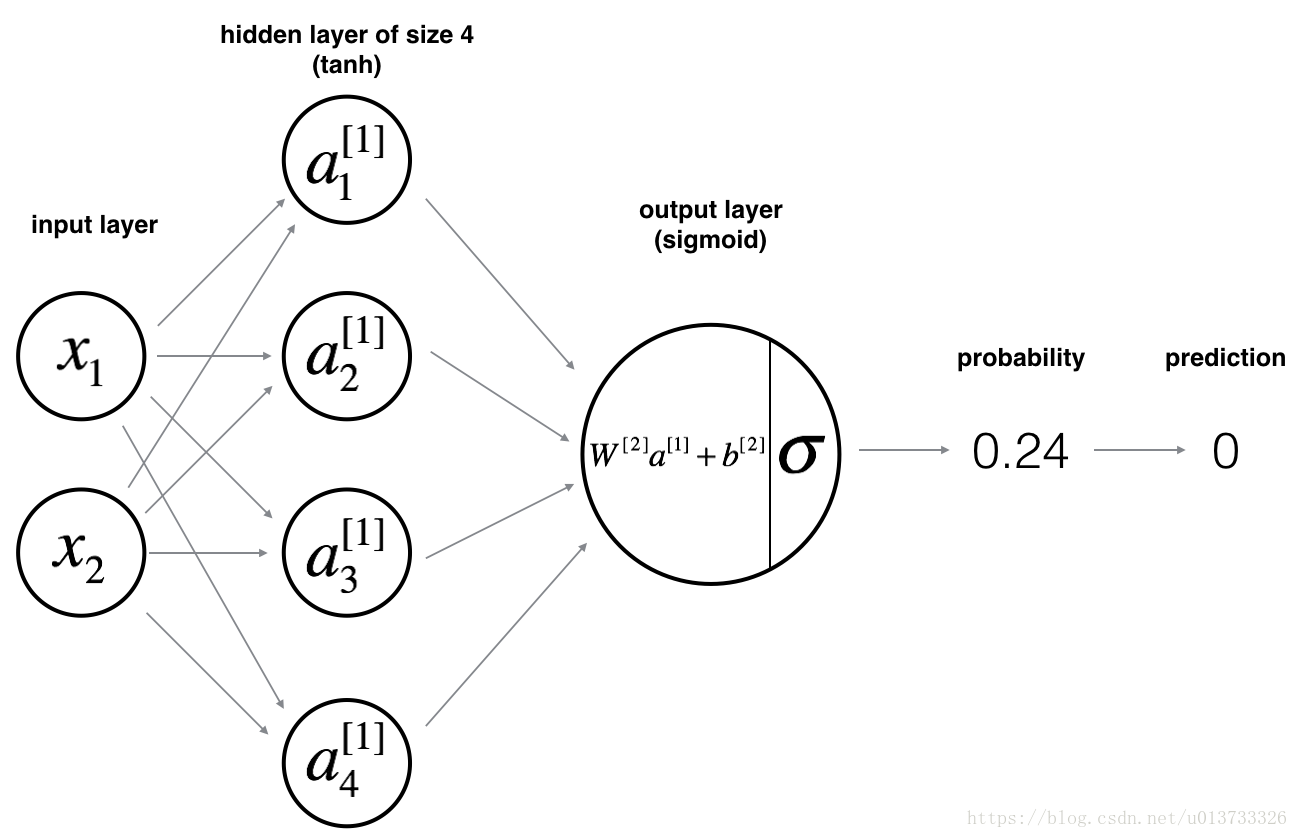
1.通常,在隐藏层使用tanh函数【优点.tanh的输出在(-1,1)之间,因此有数据中心化的效果;缺点.当z非常大或非常小时会拖慢梯度下降算法】,在输出层使用sigmoid函数【优点.我们总是想输出在(0,1)之间】
该神经网络的结构如下:
开始搭建神经网络
1. 定义神经网络结构
layer_sizes(X, Y)
该函数用来定义神经网络结构。
参数:
给定代输入的数据集X。X的结构为n*m,即m个有n个特征的样本。
给定预想输出的标签集Y。Y的结构为1*m,即m个样本对应的标签。值为0|1。
返回:
n_x - 输入层的特征数量。即n_x = X.shape[0]
n_h - 隐藏层的激活项数量。该项目设置为4,即隐藏层有4个激活项
n_y - 输出层的特征数量。即n_y = Y.shape[0]
2. 初始化模型的参数
initialize_parameters(n_x, n_h, n_y)
该函数用来初始化模型的参数。主要是对第1、2层的权值(w1、w2)和偏差(b1、b2)进行初始化。具体方案:1.利用定义神经网络结构【layer_sizes(X, Y)】返回每层的激活项数。2.根据每层激活项的个数,确定权值、偏差的矩阵维数。3.随机化矩阵。偏差b置为0
参数:
n_x - 输入层的特征数量
n_h - 隐藏层的激活项数量
n_y - 输出层的特征数量
返回:
parameters - 包含以下字段的字典:
W1 - 权重矩阵,维度为(n_h,n_x)
b1 - 偏向量,维度为(n_h,1)
W2 - 权重矩阵,维度为(n_y,n_h)
b2 - 偏向量,维度为(n_y,1)
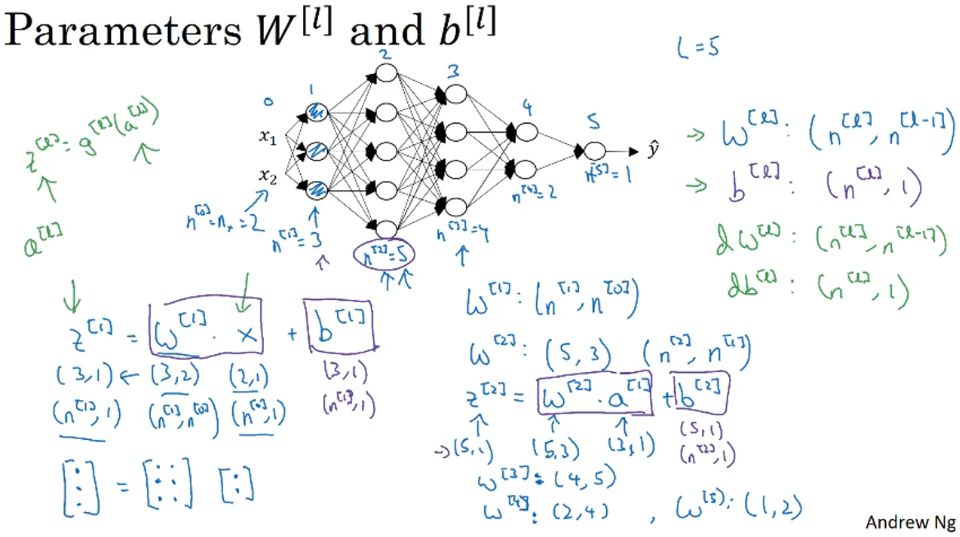
Q3. 如何确定矩阵维数,W¹:(n¹, nº),b¹:(n¹,1),dW:(n¹, nº),db:(n¹,1)
每次计算时最好是对维度预估一下,以免出错
3. Loop:
- 实施前向传播
forward_propagation(X, parameters)
该函数功能是实现前向传播。主要是利用公式计算下一阶段需要的值(Z1\Z2\A1\A2),直到计算到输出层(该模型输出层为A2)
参数:
X - 输入层的数据集(n_x,m)。
parameters - 初始化参数函数【initialize_parameters(n_x, n_h, n_y)】的初始化结果字典
返回:
A2 - 预测值
cache - 包含Z1\A1\Z2\A2的字典。反向传播时会用到。
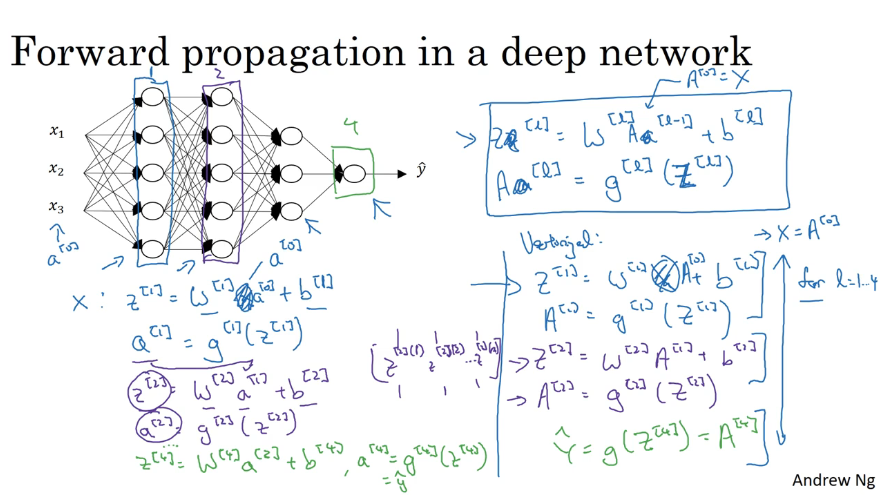
Q4. 前向传播计算公式:Z¹ = W¹X +b¹;A¹ = tanh(Z¹);Z² = W²A¹ +b²;A² = sigmoid(Z²);
- 计算损失
compute_cost(A2, Y, parameters)
该函数是用来计算在parameters的条件下,对预测值计算总损失。
参数:
A2 - 预测值
Y - 训练/测试集的标签矢量,维度为(1,训练/测试数量)
parameters - 当前模型利用的parameters # 实际没用到
返回:
成本 - 利用交叉熵损失函数进行计算的结果。通常使用np.multiply(A2,Y) or A2*Y,两种方案进行逐元素计算。
Q5. 损失计算公式:
- 实现后向传播以获得梯度
backward_propagation(parameters, cache, X, Y)
该函数功能是实现反向传播。得到参数的梯度,为后续优化参数(权值、偏差)使用。
参数:
parameters - 当前模型前向传播时使用的参数。包含W1\W2\b1\b2字段的字典
cache - 当前模型前向传播过程中计算的值。包含Z1\A1\Z2\A2的字段的字典
X - 输入层数据集
Y - 输出层标签集
返回:
grads - 包含dW1\db1\dW\db2字段的字典。
Q6. W,b的计算公式(Ng视频内容显示本就不全,非截图不全)
其中,计算db时,np.sum()需要设置:axis = 1,按行相加;keepdims = True,保持原有维度。
即得到的db.shape = (n,1)
- 更新参数(梯度下降法)
update_parameters(parameters, grads, learning_rate=1.2)
该函数是用来在对现有参数进行梯度下降,更新参数。以便于进一步进行预测。
参数:
parameters - 当前模型的使用的参数(权重、偏差)。
grads - 在当前模型下,包含dW1\dW2\db1\db2字段的字典。
learning_rate - 学习速率。决定下降的快慢。
返回:
parameters - 梯度下降之后的参数。包含W1\W2\b1\b2字段的字典
Q7. 梯度下降公式: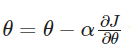
整合该训练模型
nn_model(X, Y, n_h, num_iterations, print_cost=False)将
该函数将前面的函数进行整合封装。调用该函数直接对样本进行训练。并返回参数字典,利用该字典可以对新样本进行预测。
参数:
X - 输入层数据集
Y - 输出层数据集
n_h - 隐藏层的激活项数量
num_iterations - 梯度下降循环中的迭代次数
print_cost - 如果为True,则每1000次迭代打印一次成本数值
返回:
parameters - 模型学习的参数,它们可以用来进行预测。
def nn_model(X, Y, n_h, num_iterations, print_cost=False):
np.random.seed(3) # 搭建模型用,以便与他人输出一致
# 获取输入层与输出层的特征(层)数
n_x = layer_sizes(X, Y)[0]
n_y = layer_sizes(X, Y)[2]
# 初始化参数(W\b)
parameters = initialize_parameters(n_x, n_h, n_y)
# W1, b1, W2, b2 = parameters["W1"], parameters["b1"], parameters["W2"], parameters["b2"]
# 训练参数,以获得一个更好的模型
for i in range(num_iterations):
A2, cache = forward_propagation(X, parameters) # 前向传播,获得预测值
cost = compute_cost(A2, Y, parameters) # 计算该模型损失
grads = backward_propagation(parameters, cache, X, Y) # 后向传播,获得梯度
parameters = update_parameters(parameters, grads) # 更新参数,优化模型
if print_cost: # 每1000次优化,打印损失,优化损失
if i % 1000 == 0:
print("第 ", i, " 次循环,成本为:" + str(cost))
return parameters # 返回训练好的参数,以便预测新样本封装预测函数
predict(parameters, X)
使用学习的参数,为X(新样本集)预测
参数:
parameters - 训练好的参数(权值、偏差)
X - 输入新样本(与训练集的特征(层)数量保持一致)
返回
predictions - 我们模型预测结果(二分类问题:0|1)
Q8. 输出层输出时,对输出值进行控制为0|1。np.round()进行实现。前面计算损失不需要进行数据处理,求真实的误差。predict() 如下:
def predict(parameters, X):
A2, cache = forward_propagation(X, parameters)
predictions = np.round(A2) # 四舍五入,让输出值为0|1
return predictions总结
| 对神经网络结构每层的特征数量进行定义 | 整合模型 | 预测新样本 | |
| 初始化参数(权值、偏差) | |||
| 迭代 | 前向传播,得输出值,存中 间值 | ||
| 计算损失 | |||
| 后向传播,得梯度 | |||
| 梯度下降法,更新参数 | |||
参考文献
2. 吴恩达 DeepLearning.ai课程