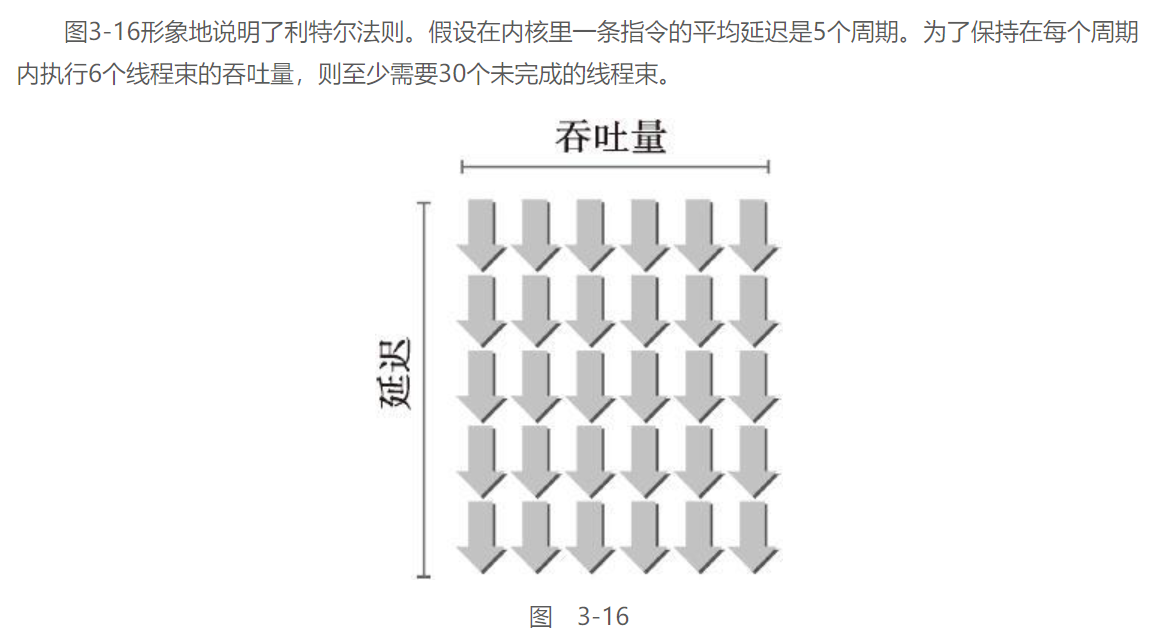
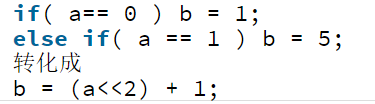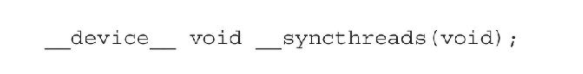CUDA编程第三章: CUDA执行模型

前言:

本章内容：

通过配置文件驱动的方法优化内核
理解线程束执行的本质
增大GPU的并行性
掌握网格和线程块的启发式配置
学习多种CUDA的性能指标和事件
了解动态并行与嵌套执行

通过上一章的练习, 你已经学会了如何在网格和线程块中组织线程以获得最佳的性能. 尽管可以通过反复试验找到最佳的执行配置, 但你可能仍然会感到疑惑, 为什么选择这样的执行配置会更好. 你可能想知道是否有一些选择网格和块配置的准则. 本章将会回答这些问题, 并从硬件方面深入介绍内核启动配置和性能分析的信息.

3.1 CUDA执行模型概述:

CUDA执行模型揭示了GPU并行架构的抽象视图, 使我们能够据此分析线程的并发

在第2章里, 已经介绍了CUDA编程模型中两个主要的抽象概念：内存层次结构和线程层次结构。它们能够控制大规模并行GPU。因此, CUDA执行模型能够提供有助于在指令吞吐量和内存访问方面编写高效代码的见解

在本章会重点介绍指令吞吐量, 在第4章和第5章里会介绍更多的关于高效内存访问的内容。

GPU架构概述:

GPU架构是围绕一个流式多处理器（SM）的可扩展阵列搭建的。可以通过复制这种架构的构建块来实现GPU的硬件并行

由于教程书年份为2014, 所以分析的是Fermi架构

其余架构可以看NVIDIA官网:

https://docs.nvidia.com/cuda/

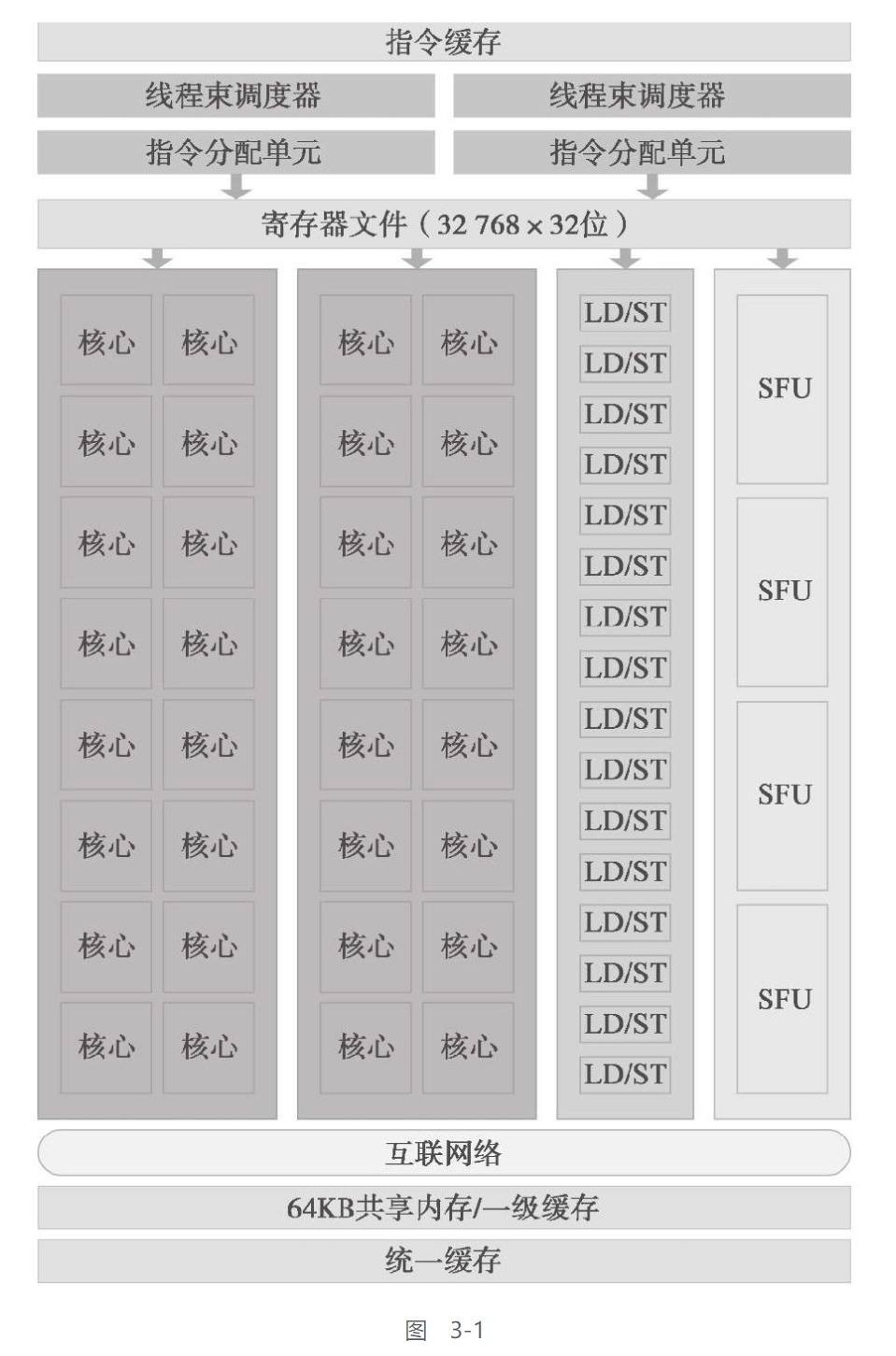
以下展示了Fermi SM的关键组件：

CUDA核心
共享内存/一级缓存
寄存器文件
加载/存储单元
特殊功能单元
线程束调度器

这里添加一个Pascal架构核心图:

服务器上使用的P100 是GP100核心, 本地环境中的GTX1050是GP107核心(砍得只剩这么点了, 并且6个SM核心还被屏蔽了一个)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-661FYXbR-1612324765768)(https://img2.ali213.net/hardware/news/2016/10/25/2016102542443813.jpg)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Gv4xTsGw-1612324765770)(https://img2.ali213.net/hardware/news/2016/10/25/2016102542606448.jpg)]

GPU中的每一个SM都能支持数百个线程并发执行，每个GPU通常有多个SM

当启动一个内核网格时，它的线程块被分布在了可用的SM上来执行。线程块一旦被调度到一个SM上，其中的线程只会在那个指定的SM上并发执行
多个线程块可能会被分配到同一个SM上，而且是根据SM资源的可用性进行调度的。同一线程中的指令利用指令级并行性进行流水线化

CUDA采用单指令多线程（SIMT）架构来管理和执行线程，每32个线程为一组，被称为线程束（warp）。线程束中的所有线程同时执行相同的指令。每个线程都有自己的指令地址计数器和寄存器状态，利用自身的数据执行当前的指令。每个SM都将分配给它的线程块划分到包含32个线程的线程束中，然后在可用的硬件资源上调度执行。

SIMD & SIMT :

两者都是将相同的指令广播给多个执行单元来实现并

一个关键的区别是SIMD要求同一个向量中的所有元素要在一个统一的同步组中一起执行，而SIMT允许属于同一线程束的多个线程独立执行。尽管一个线程束中的所有线程在相同的程序地址上同时开始执行，但是单独的线程仍有可能有不同的行为。SIMT确保可以编写独立的线程级并行代码、标量线程以及用于协调线程的数据并行代码。

SIMT模型包含3个SIMD所不具备的关键特征。

每个线程都有自己的指令地址计数器
每个线程都有自己的寄存器状态
每个线程可以有一个独立的执行路径

一个神奇的数字: 32

CUDA中很长用到32

从概念上讲，它是SM用SIMD方式所同时处理的工作粒度。优化工作负载以适应线程束（一组有32个线程）的边界，一般这样会更有效地利用GPU计算资源。在后面的章节中将会介绍更多这方面的内容。

一个线程块只能在一个SM上被调度。一旦线程块在一个SM上被调度，就会保存在该SM上直到执行完成。
在同一时间，一个SM可以容纳多个线程块
尽管线程块里的所有线程都可以逻辑地并行运行，但是并不是所有线程都可以同时在物理层面执行, 活跃的线程束数量受SM资源限制。因此，线程块里的不同线程可能会以不同的速度前进

对于数据竞争:

CUDA提供了一种用来同步线程块里的线程的方法

然而，没有提供块间同步的原语

尽管线程块里的线程束可以任意顺序调度，但活跃的线程束的数量还是会由SM的资源所限制。当线程束由于任何理由闲置的时候（如等待从设备内存中读取数值），SM可以从同一SM上的常驻线程块中调度其他可用的线程束。在并发的线程束间切换并没有开销，因为硬件资源已经被分配到了SM上的所有线程和块中，所以最新被调度的线程束的状态已经存储在SM上。

Fermi架构:

费米架构贼老了, 基本不会用上Fermi架构的显卡, 但是其架构的特点被沿用到了之后的几代显卡架构中, 所以还是很有必要学一下的

CUDA核心:

CUDA核心可以看做是GPU中的处理单元

每个CUDA核心都有一个全流水的整数算数逻辑单元(ALU)和一个浮点运算单元(FPU), 并且在一个时钟周期执行一个整数或浮点数指令

在Fermi架构中, CUDA核心被继承到了16个SM单元中, 每个SM还有32个CUDA核心
SM单元:

一个SM，包含了以下内容：
- 32个CUDA核心执行单元
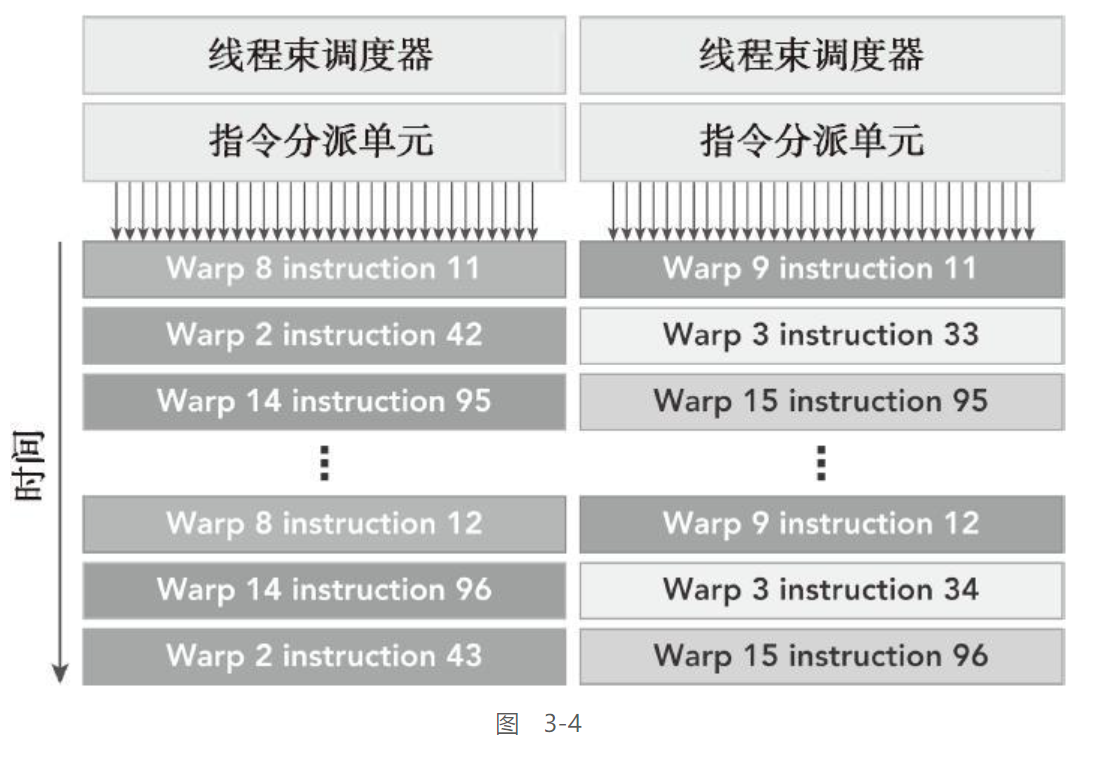
- 2个线程数调度器 & 2个指令调度单元
  
  一个线程块被指定给一个SM时，线程块中的所有线程被分成了线程束。两个线程束调度器选择两个线程束，再把一个指令从线程束中发送到一个组上，组里有16个CUDA核心、16个加载/存储单元或4个特殊功能单元
- 共享内存、寄存器文件和一级缓存
  
  共享内存是影响应能的一个关键因素, 其允许一个块上的线程相互合作, 有利于芯片内数据的复用, 并大大降低了片外通信量
  
  CUDA体用了一个Runtime API 用于调整共享内存和以及缓存的数量
- 16个LD/ST单元
  允许每个时钟周期内有16个线程计算源地址和目的地址
- SFU特殊功能单元:
  用于执行固有指令, 如正弦, 余弦, 平方根&差值
  每个SFU在每个时钟周期内的每个线程上执行一个固有指令

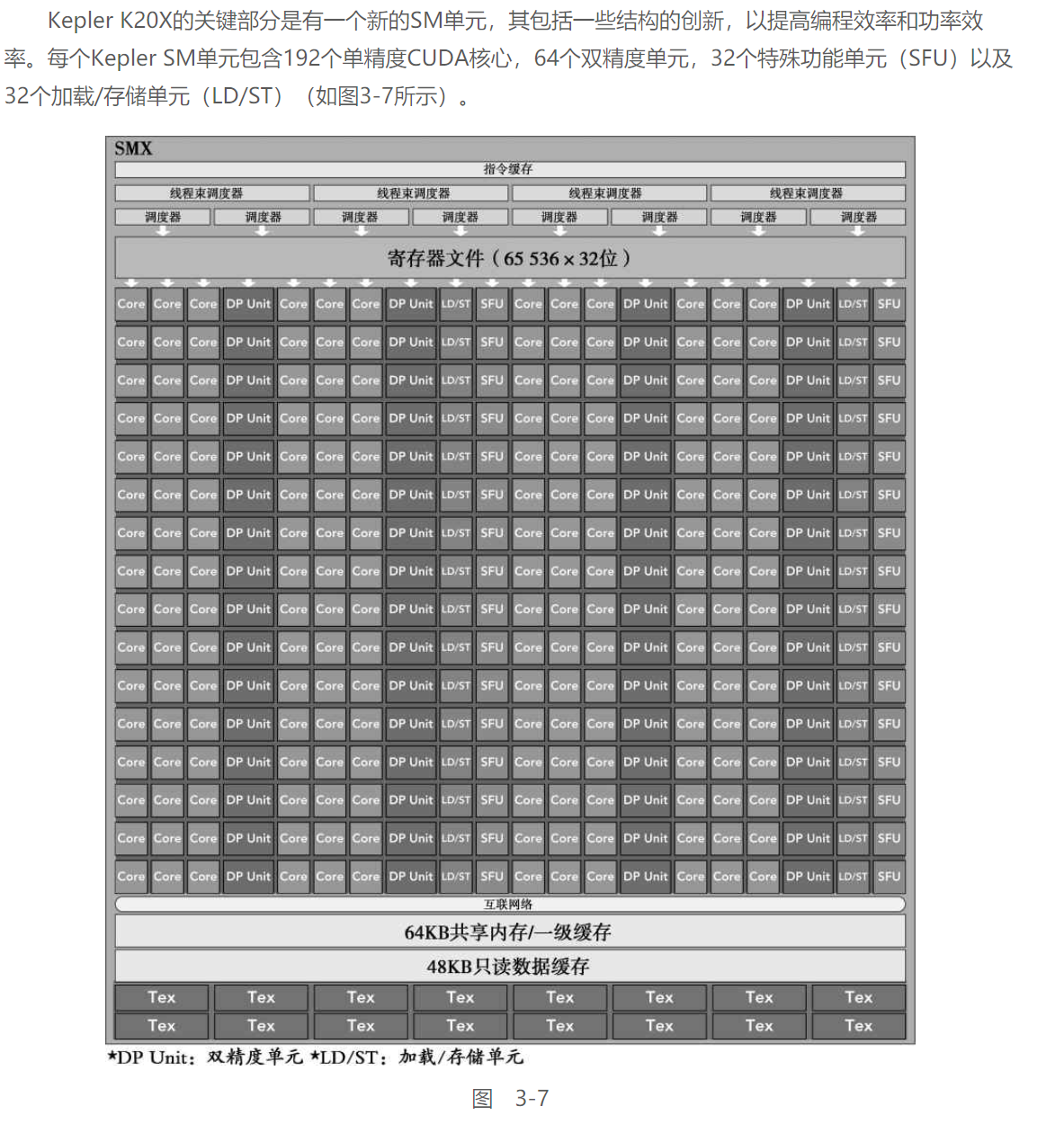
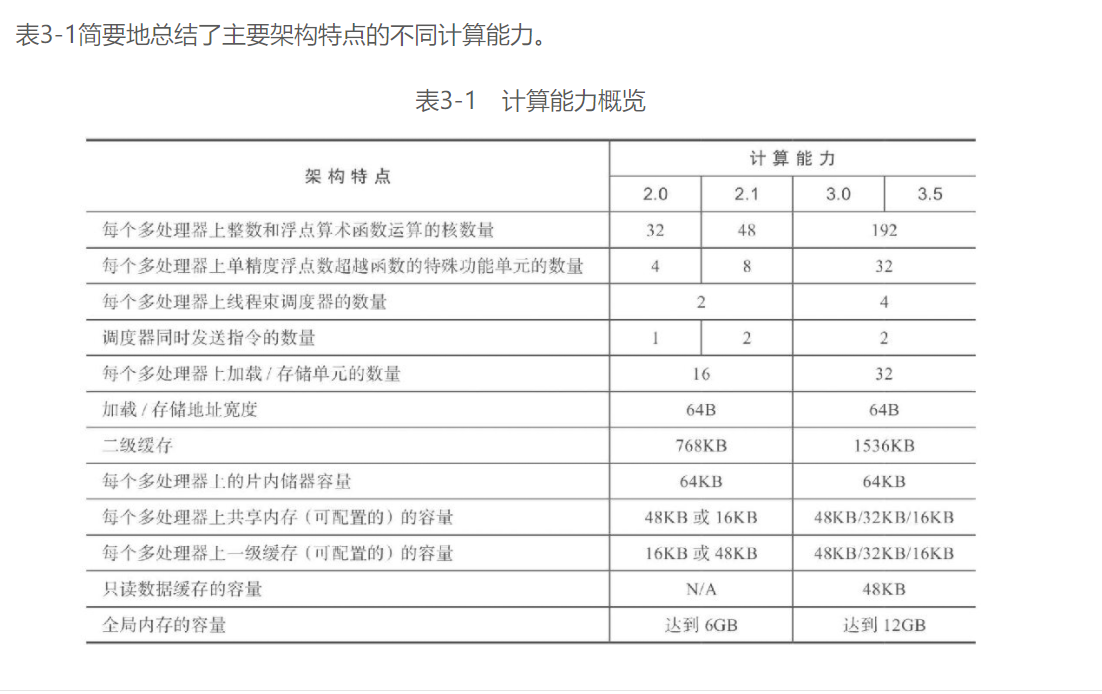
Kepler架构:

由于会用服务器上的K20跑程序, 这里重点学习一下Kepler架构

每个Kepler SM包括4个线程束调度器和8个指令调度器，以确保在单一的SM上同时发送和执行4个线程束
Kepler K20X架构可以同时在每个SM上调度64个线程束，即在一个SM上可同时常驻2048个线程
K20X架构中寄存器文件容量达到64KB
K20X还允许片内存储器在共享内存和一级缓存间有更多的分区
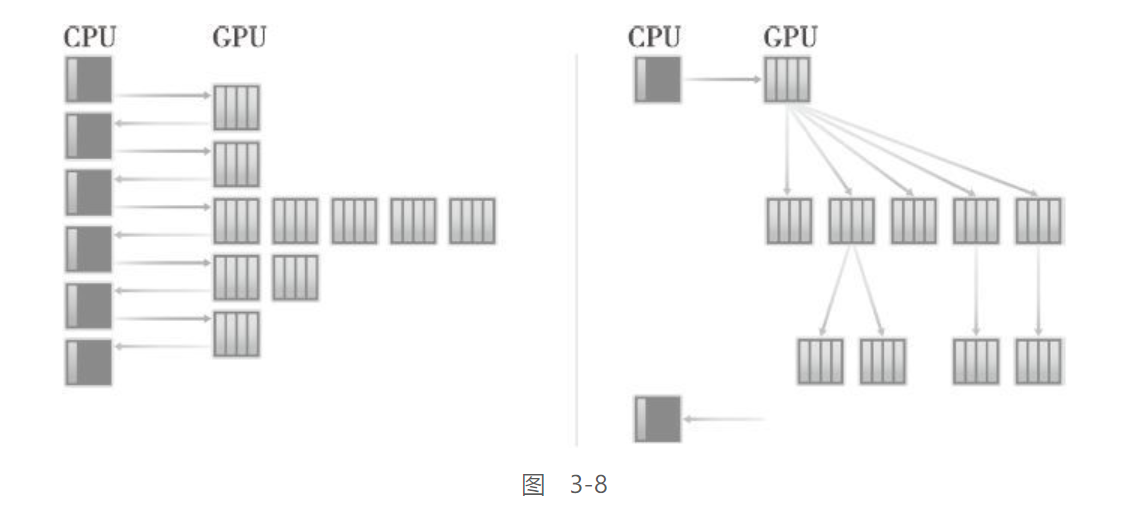
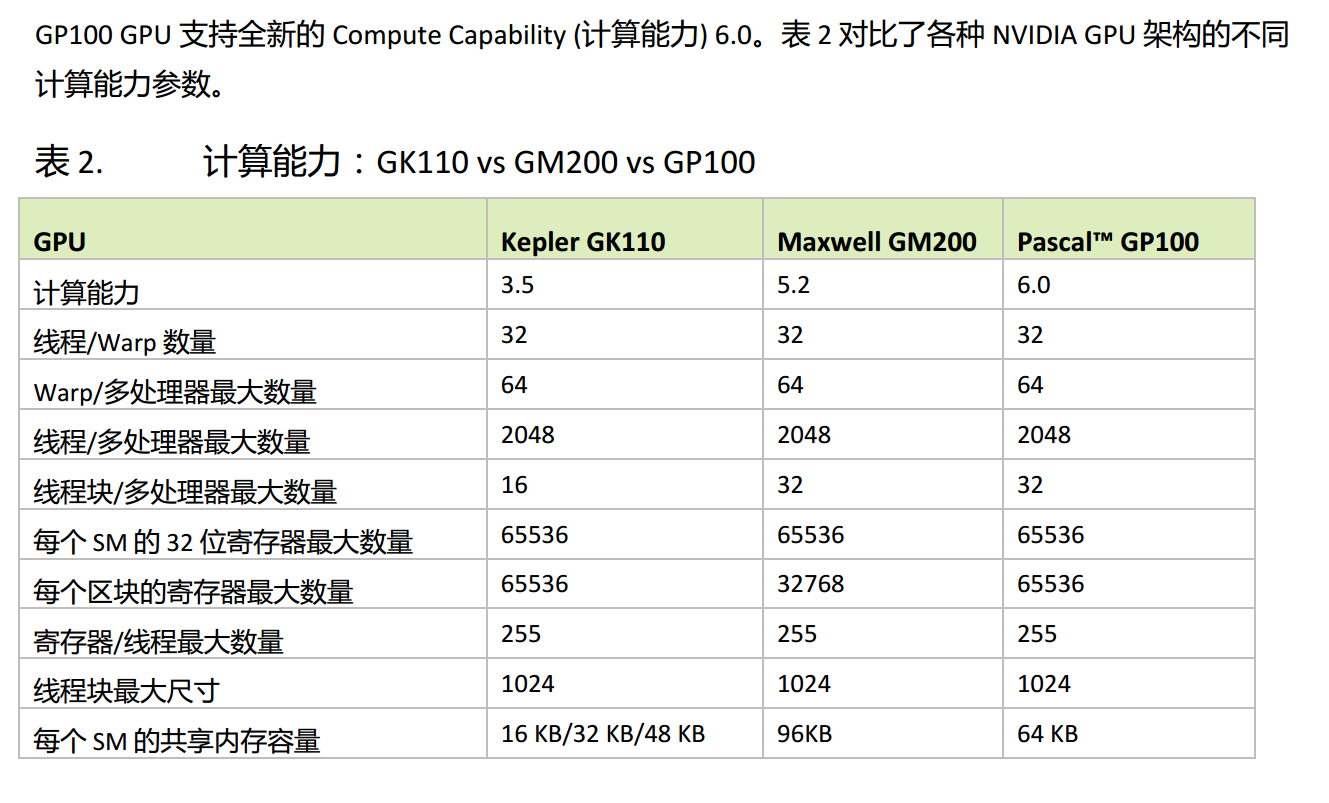
Kelper支持了动态并行技术, 它允许GPU动态启动新的网格

任一内核都能启动其他的内核，并且管理任何核间需要的依赖关系来正确地执行附加的工作

如图所示, 没有动态并行时, 需要主机的控制才能启动GPU内核
而加入了动态并行后, GPU能够嵌套的启动内核, 消除了与CPU通信的需求
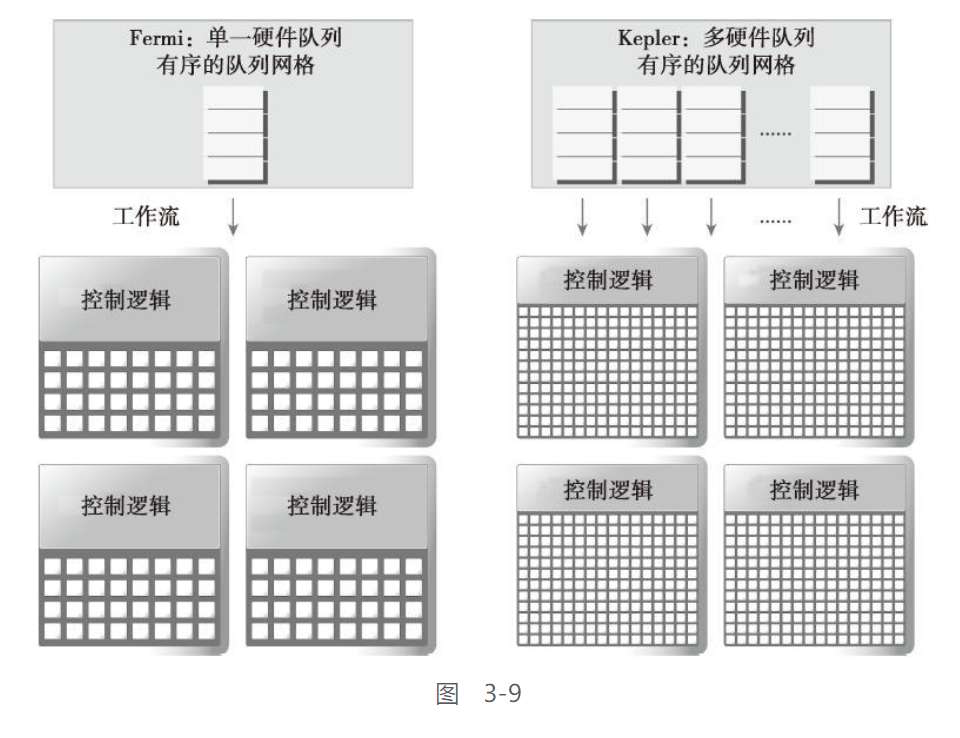
Kepler还提出了Hyper-Q技术

Hyper-Q技术增加了更多的CPU和GPU之间的同步硬件连接，以确保CPU核心能够在GPU上同时运行更多的任务, 能增加GPU的利用率, 并减少CPU的空闲时间

举个栗子:

Fermi架构中, GPU依赖一个单一的硬件工作队列来从CPU到GPU中传送数据, 这可能导致一个单独的任务阻塞该任务之后的所有任务, Kepler消除了这个限制, 其提供了32个硬件工作队列, 保证了GPU上有更多的并发执行, 最大限度的提高了GPU的利用率

本部分的作用还不是很清楚, 只能是照抄了

Pascal架构:

由于使用的是GTX1050 & P100显卡, 这里添加一个书里没有的Pascal架构

这里整体参考NVIDIA发布的白皮书, 以GP100核心为基准

本部分看了一半, 剩余的等后头多学一点再来

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-42dvkPBh-1612324765788)(https://img2.ali213.net/hardware/news/2016/10/25/2016102542443813.jpg)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IKuU6tnt-1612324765789)(https://img2.ali213.net/hardware/news/2016/10/25/2016102542606448.jpg)]

GP100性能:

NVLink:

老黄在Pascal架构发布的同时也带来了NVLink技术, 一种超越PCI-e带宽的GPU连接技术, 能够最高达到PCIe3.0x16带宽的5倍, 双向带宽达到160GB/s

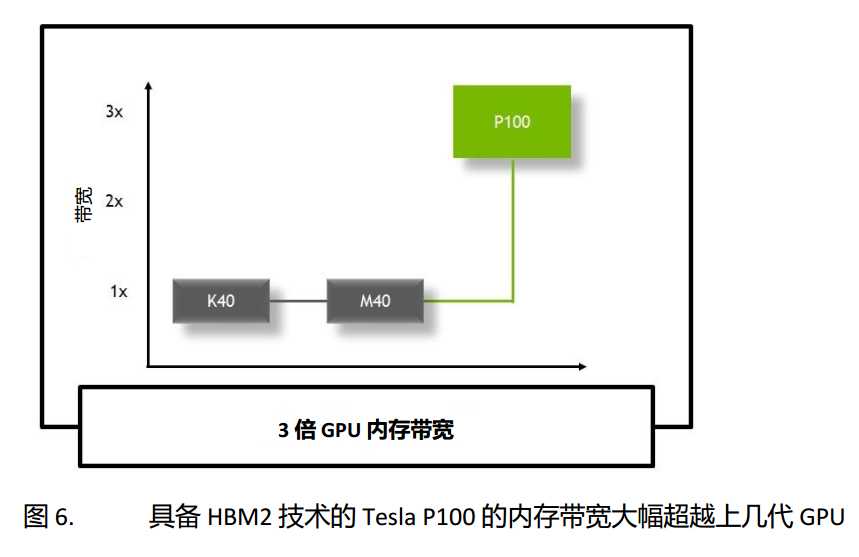
HBM2 高速GPU架构:

其相比于GDDR5X, HBM2从硬件上实现了ECC校验, 并且显存带宽达到GM200的三倍

统一内存 & 计算抢占:

统一内存相当于统一了CPU与GPU的内存空间, 为CPU 和 GPU 内存提供无缝统一癿单一虚拟地址穸间

其大幅简化了GPU编程和应用程序向GPU移植的过程，而且还能够缩短GPU计算的学习用时。程序员不再需要担心如何在两种不同的虚拟内存系统之间管理数据共享。GP100是支持硬件页错误（Page Faulting）的首款NVIDIA GPU，当它与全新的49位（512 TB）虚拟寻址相结合时，能够在GPU和CPU的全部虚拟地址空间之间实现透明数据迁移

计算抢占（Compute Preemption）是添加到GP100中的另一项重要的全新软硬件特性，它能够以指令级间隔抢占计算任务，而非使用之前Maxwell和kepler GPU架构中的线程块间隔。计算抢占可防止长期运行的应用程序独占系统（防止其它应用程序运行）或超时。程序员不再需要修改其长期运行的应用程序即可使其很好地兼容其它GPU应用程序。凭借GP100中的计算抢占，应用程序可以在需要的时候运行以处理大型数据集或者在与其它任务一起调度时等待各种条件出现。例如，互动图形任务和互动调试程序均可以与长期运行的计算任务一起运行。

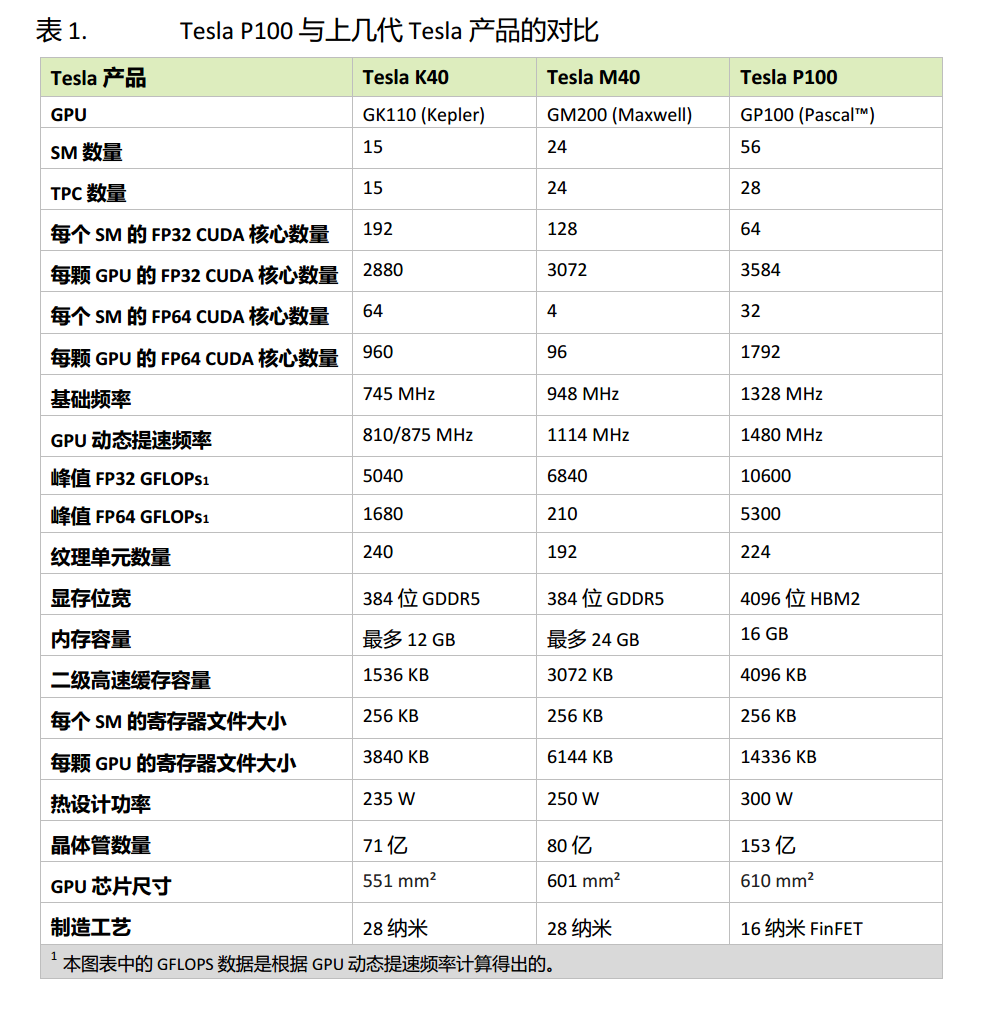
性能对比:

Pascal SM:

配置文件驱动优化:

本部分涉及代码的性能分析&优化:

性能分析是通过检测来分析程序性能的行为：

应用程序代码的空间（内存）或时间复杂度
特殊指令的使用
函数调用的频率和持续时间

性能分析是程序开发中的关键一步，特别是对于优化HPC应用程序代码。性能分析往往需要对平台的执行模型有一个基本的理解以制定应用程序的优化方法。

对于性能优化, 通常使用配置文件驱动完成

配置文件驱动的发展对于CUDA编程尤为重要，原因主要有以下几个方面。

一个单纯的内核应用一般不会产生最佳的性能。性能分析工具能帮助你找到代码中影响性能的关键部分，也就是性能瓶颈。
CUDA将SM中的计算资源在该SM中的多个常驻线程块之间进行分配。这种分配形式导致一些资源成为了性能限制者。性能分析工具能帮助我们理解计算资源是如何被利用的。
CUDA提供了一个硬件架构的抽象，它能够让用户控制线程并发。性能分析工具可以检测和优化，并将优化可视化。

CUDA提供两个主要的性能分析工具:

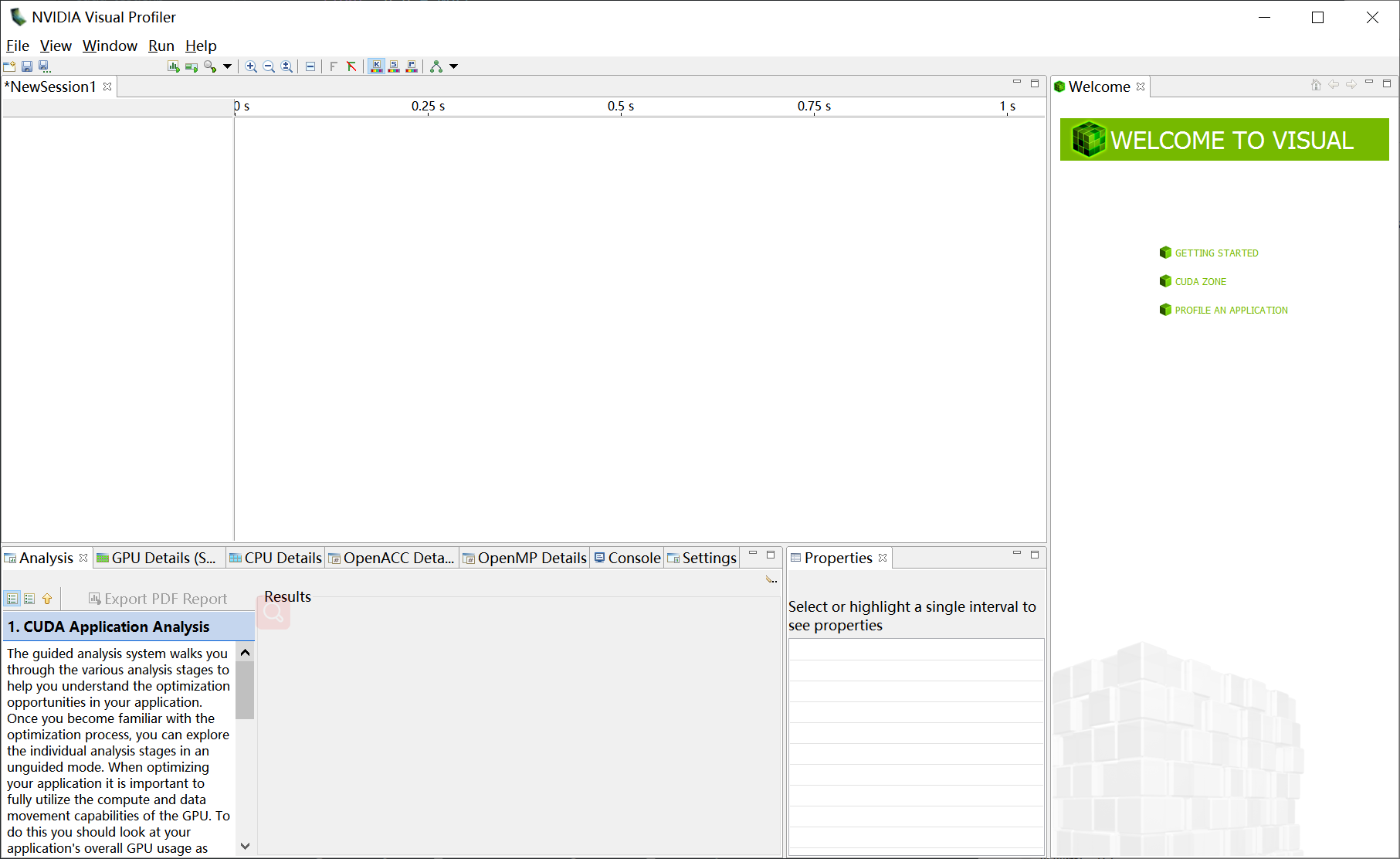
nvvp
独立的可视化分析器

nvvp是可视化分析器，它可以可视化并优化CUDA程序的性能。这个工具会显示CPU与GPU上的程序活动的时间表，从而找到可以改善性能的机会。此外，nvvp可以分析应用程序潜在的性能瓶颈，并给出建议以消除或减少这些瓶颈。
nvprof
命令行分析器

它可以获得CPU与GPU上CUDA关联活动的时间表，其中包括内核执行、内存传输和CUDA的API调用。它也可以获得硬件计数器和CUDA内核的性能指标

事件 & 指标:

本部分很迷, 不知道在讲啥

大多数计数器通过流式多处理器来报告，而不是通过整个GPU。
一个单一的运行只能获得几个计数器。有些计数器的获得是相互排斥的。多个性能分析运行往往需要获取所有相关的计数器。
由于GPU执行中的变化（如线程块和线程束调度指令），经重复运行，计数器值可能不是完全相同的。

有3种常见的限制内核性能的因素：

存储带宽
计算资源
指令和内存延迟

本章主要介绍指令延迟的问题，其次会介绍一些计算资源限制的问题。

3.2 理解线程束的本质:

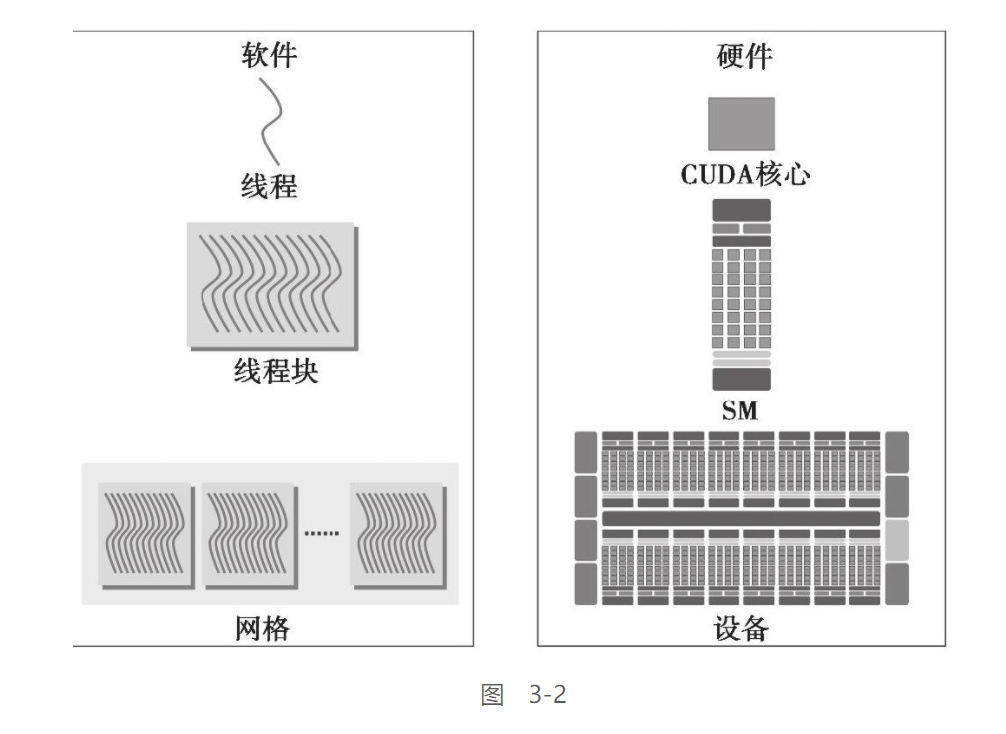
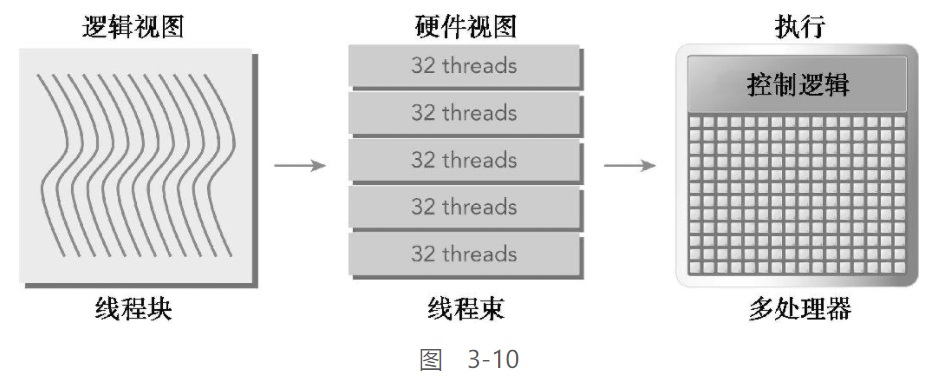
线程束 & 线程块:

线程块的逻辑视图 & 硬件视图的关系

从逻辑的角度上看

线程块是线程的有序集合, 能够通过blockDim设置成一维, 二维, 三维

每个线程都有唯一的ID, 通过threadIdx中的三个分量计算得到

从物理的角度上看

不论是几维的线程块, 在物理上都会被组织成一维布局

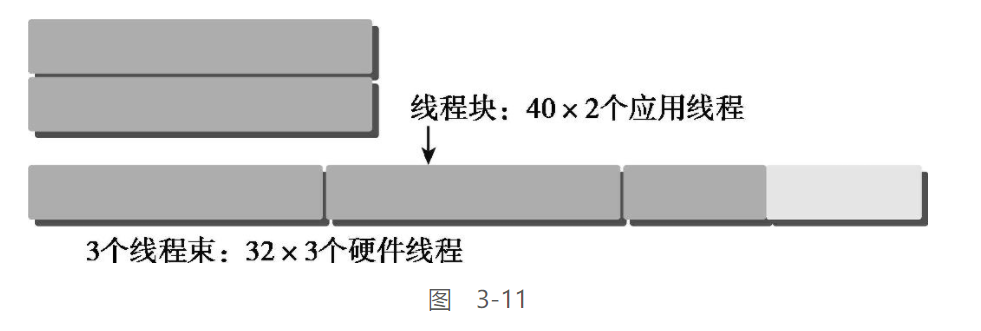
对于线程束, 硬件总是给一个线程块分配一定数量的线程束, 并且总是以32个为一组

这里的warp即线程束的意思:

当线程数数量不足时, 硬件仍然会使用32的整数倍去分配线程, 如对于80个软件线程, 硬件会使用96个硬件线程去支持, 但部分线程是不活跃的, 即使这些线程未被使用，它们仍然消耗SM的资源，如寄存器

线程束分化:

与CPU相比, GPU的SM更为简单, 没有分支预测, 所以

一个线程束中的所有线程在同一周期中必须执行相同的指令，如果一个线程执行一条指令，那么线程束中的所有线程都必须执行该指令

如果在同一线程束中的线程使用不同的路径通过同一个应用程序，这可能会产生线程束分化问题

if (cond){
    ...
}else{
    ...
}

如以上代码, 一个线程束中有一半(16个)线程cond==true, 其余的cond==false , 这就会导致线程束分化问题

GPU在执行时, 仅会按照一个路径执行下去, 其余的分支暂时等待

即, 在如上的例子中, 先会执行前16个进程, 而剩余的16个进程进入等待状态, 这会导致性能的严重下降, 并且分支数越多, 性能越差

会有如下效果:

规避线程束分化:

避免的方法就是在编码的时候, 注意分支情况, 调整分支粒度仪适应线程束大小的倍数, 使得一个线程束中的所有线程执行同一个路径

更常用的方法是使用查找表来去掉某些分支, 或是将分支转化为计算:

上头的第一部分中说明了线程块中线程束的划分规则, 这里就是利用这个规则进行分支的划分:

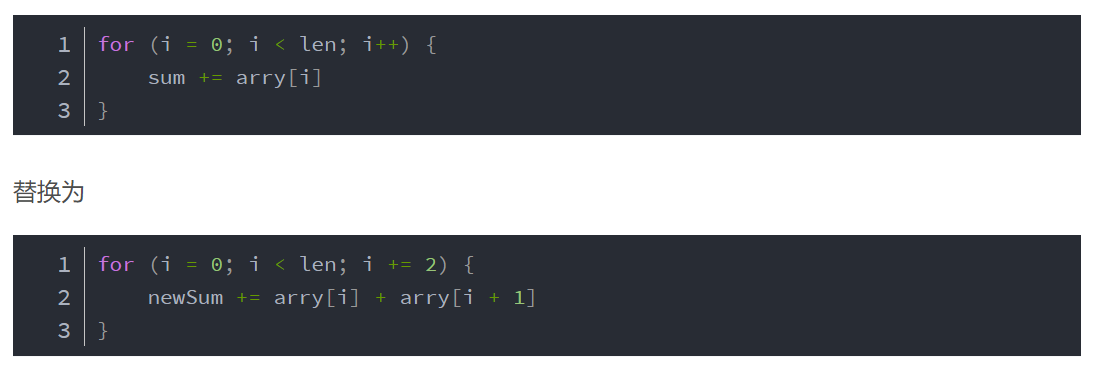
如这个代码:

他根据线程tid号的奇偶进行分支, 这会导致线程束分化

变更之后的代码如下:

将所有执行if部分的线程归并到同一个线程束中, warpSize为CUDA自带变量

实际上, CUDA编译器会自动检测一些分支, 并进行一定程度的优化, 将短的, 有条件的代码段的分支指令替换为了断定指令, 规避了实际的分化控制流

分支效率:

这个分支效率中的分支数 & 分化分支数搞不懂啊, 这俩是啥?

计算分支代码效率有一个专门的计算公式:

例子:

本部分直接Copy书中的例子, 这个例子演示了 线程束分化 & CUDA编译器的优化

#include <cuda_runtime.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>


__global__ void mathKernel1(float *c)
{
    int tid = blockIdx.x * blockDim.x + threadIdx.x;
    float a, b;
    a = b = 0.0f;
    if (tid % 2 == 0)
    {
        a = 100.0f;
    }
    else
    {
        b = 200.0f;
    }
    c[tid] = a + b;
}

__global__ void mathKernel2(float *c)
{
    int tid = blockIdx.x * blockDim.x + threadIdx.x;
    float a, b;
    a = b = 0.0f;
    if ((tid / warpSize) % 2 == 0)
    {
        a = 100.0f;
    }
    else
    {
        b = 200.0f;
    }
    c[tid] = a + b;
}

__global__ void warmingup(float *c)
{
    int tid = blockIdx.x * blockDim.x + threadIdx.x;
    float a, b;
    a = b = 0.0f;
    if ((tid / warpSize) % 2 == 0)
    {
        a = 100.0f;
    }
    else
    {
        b = 200.0f;
    }
    c[tid] = a + b;
}

int main(int argc, char **argv)
{
    // set up device
    int dev = 0;
    cudaDeviceProp deviceProp;
    cudaGetDeviceProperties(&deviceProp, dev);
    printf("%s using Device %d: %s\n", argv[0], dev, deviceProp.name);
    // set up data size
    int size = 64;
    int blocksize = 64;
    if (argc > 1)
        blocksize = atoi(argv[1]);
    if (argc > 2)
        size = atoi(argv[2]);
    printf("Data size %d ", size);
    // set up execution configuration
    dim3 block(blocksize, 1);
    dim3 grid((size + block.x - 1) / block.x, 1);
    printf("Execution Configure (block %d grid %d)\n", block.x, grid.x);
    // allocate gpu memory
    float *d_C;
    size_t nBytes = size * sizeof(float);
    cudaMalloc((float **)&d_C, nBytes);
    // run a warmup kernel to remove overhead
    size_t iStart, iElaps;
    cudaDeviceSynchronize();
    iStart = clock();
    warmingup<<<grid, block>>>(d_C);
    cudaDeviceSynchronize();
    iElaps = clock() - iStart;
    printf("warmup <<< %4d %4d >>> elapsed %d sec \n", grid.x, block.x, iElaps);
    // run kernel 1
    iStart = clock();
    mathKernel1<<<grid, block>>>(d_C);
    cudaDeviceSynchronize();
    iElaps = clock() - iStart;
    printf("mathKernel1 <<< %4d %4d >>> elapsed %d sec \n", grid.x, block.x, iElaps);
    // run kernel 3
    iStart = clock();
    mathKernel2<<<grid, block>>>(d_C);
    cudaDeviceSynchronize();
    iElaps = clock() - iStart;
    printf("mathKernel2 <<< %4d %4d >>> elapsed %d sec \n", grid.x, block.x, iElaps);
    // // run kernel 3
    // iStart = seconds();
    // mathKernel3<<<grid, block>>>(d_C);
    // cudaDeviceSynchronize();
    // iElaps = seconds() - iStart;
    // printf("mathKernel3 <<< %4d %4d >>> elapsed %d sec \n", grid.x, block.x, iElaps);
    // // run kernel 4
    // iStart = seconds();
    // mathKernel4<<<grid, block>>>(d_C);
    // cudaDeviceSynchronize();
    // iElaps = seconds() - iStart;
    // printf("mathKernel4 <<< %4d %4d >>> elapsed %d sec \n", grid.x, block.x, iElaps);
    // free gpu memory and reset divece
    cudaFree(d_C);
    cudaDeviceReset();
    return EXIT_SUCCESS;
}

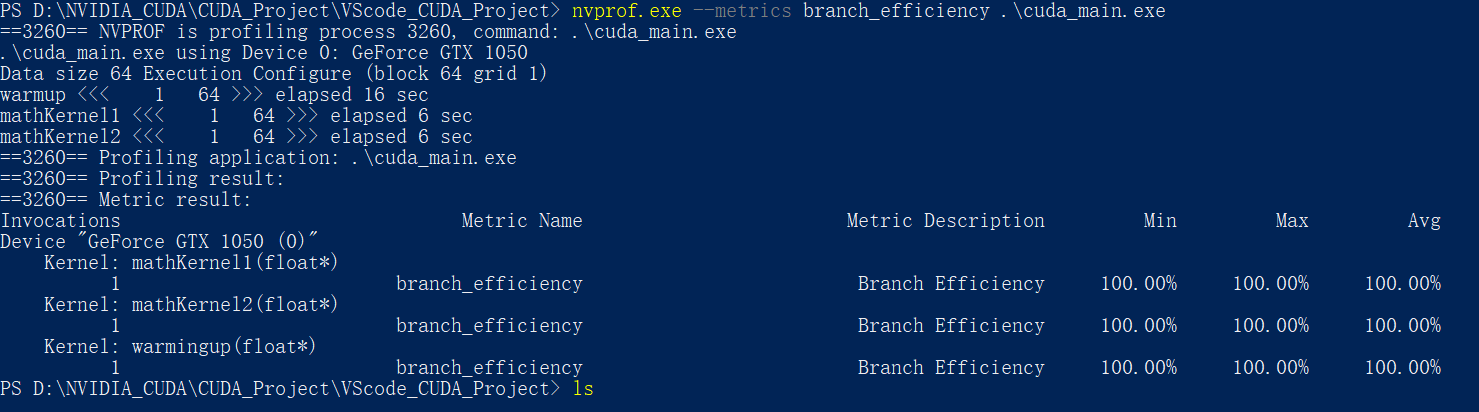
使用nvprof检测出的结果也是分支效率100%

这里的Branch Efficiency 是专门用来进行分支预测效率计算的

并且, 在windows 419.17版本之后, 由于安全问题, GPU性能分析受限, 必须以管理员身份运行才能解决

详见这里:

https://developer.nvidia.com/nvidia-development-tools-solutions-err_nvgpuctrperm-permission-issue-performance-counters

输出:

这里就是CUDA编译器优化的结果了

取消NVCC分支优化:

使用如下命令可以取消nvcc对分支的优化:

nvcc -g -G .\cuda_main.cu -o cuda_main.exe

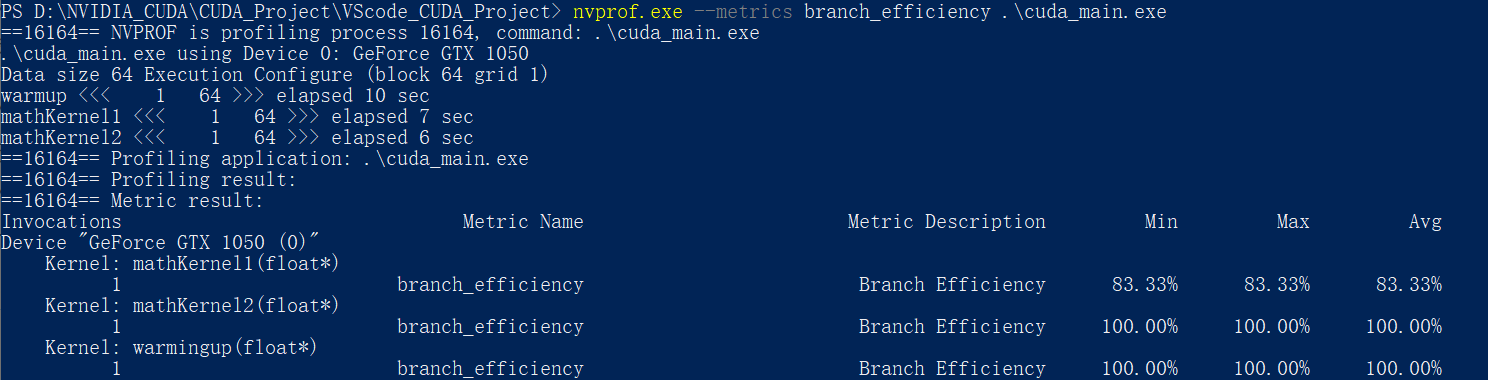
再次nvprof之后:

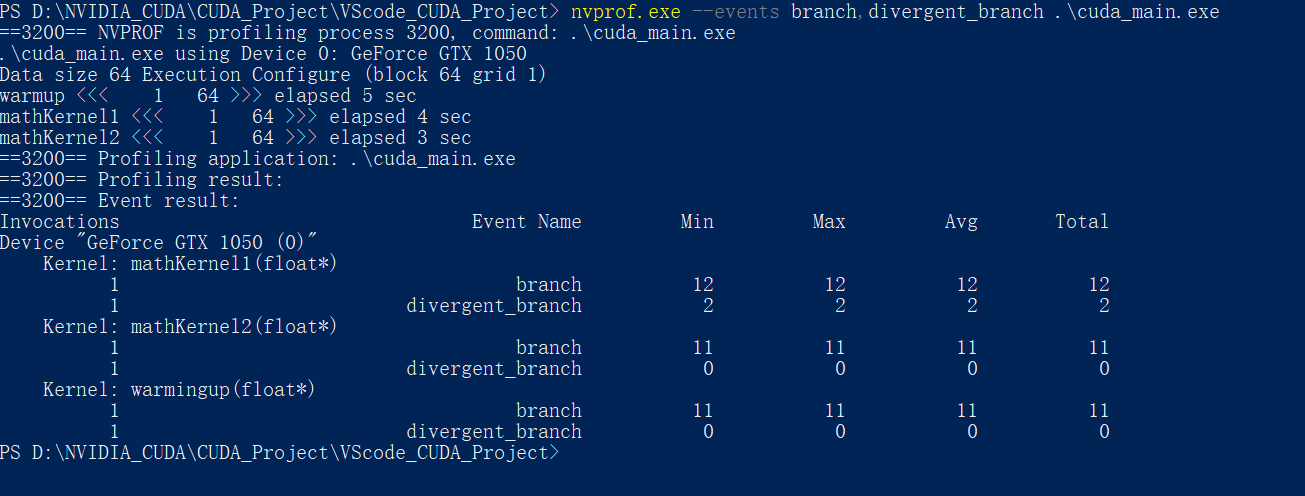
获取分支&分化分支计数器:

就是上头的分支效率计算中的两个变量:

nvprof.exe --events branch,divergent_branch .\cuda_main.exe

nvprof:

资源分配:

之前讲到, 每个SM上都会有常驻的线程块, 而线程束根据这些常驻线程块进行分配的

线程束的本地执行上下文主要由以下资源组成：

程序计数器
寄存器
共享内存

在线程束的生存期中, 线程束的上下文是常驻在SM中的, 所以上下文切换基本没有损失

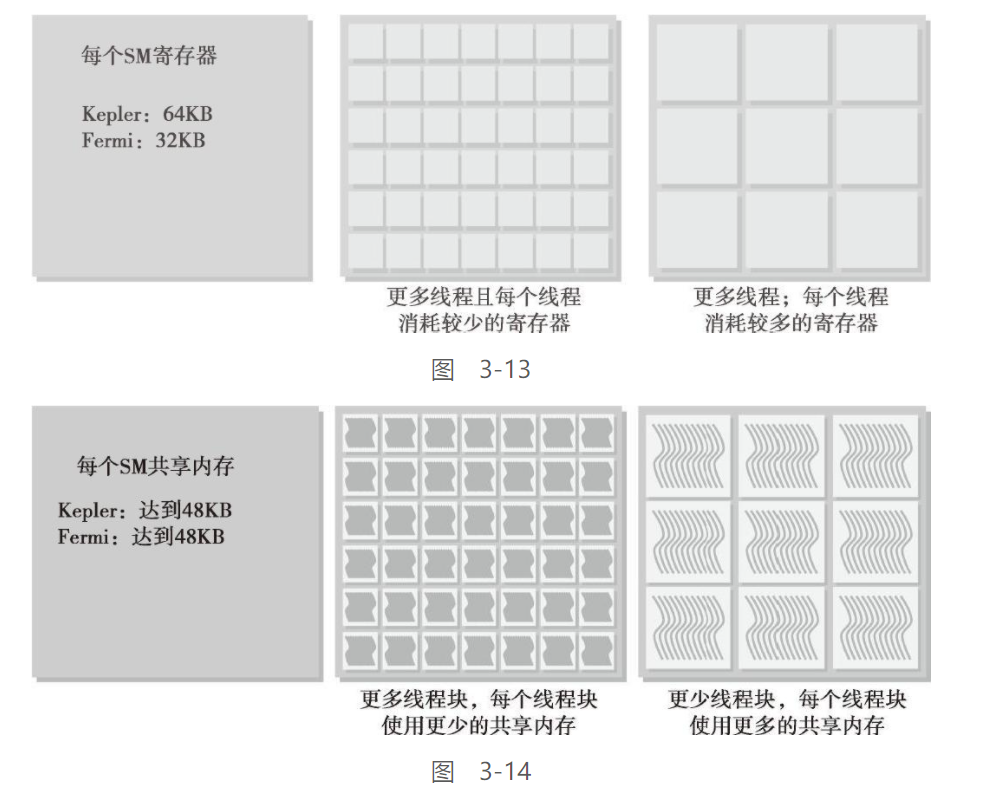
正因为如此, SM中常驻线程的数量与线程占用的寄存器 & 共享内存的关系成反比

如果SM没有足够的寄存器或共享内存去处理至少一个线程块, 则内核将无法启动

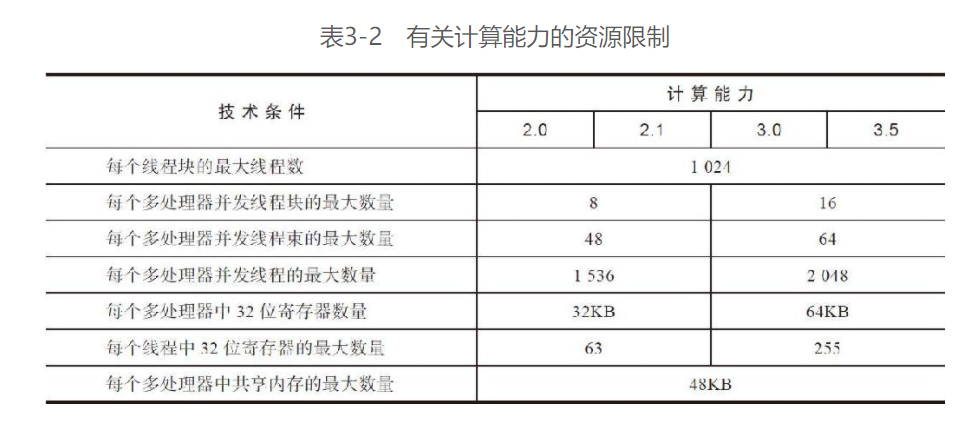
下标展现一些关键的限制因素:

活跃块 & 活跃线程束:

当计算资源（如寄存器和共享内存）已分配给线程块时，线程块被称为活跃的块。它所包含的线程束被称为活跃的线程束。一个SM上的线程束调度器在每个周期都选择活跃的线程束，然后把它们调度到执行单元

活跃的线程束可以进一步被分为以下3种类型：

选定的线程束
活跃执行的线程束被称为选定的线程束
阻塞的线程束
没有做好执行的准备的线程束是阻塞的线程束
符合条件的线程束
准备执行但尚未执行的线程束是一个符合条件的线程束

线程束符合执行的条件

32个CUDA核心可用于执行
当前指令中所有的参数都已就绪

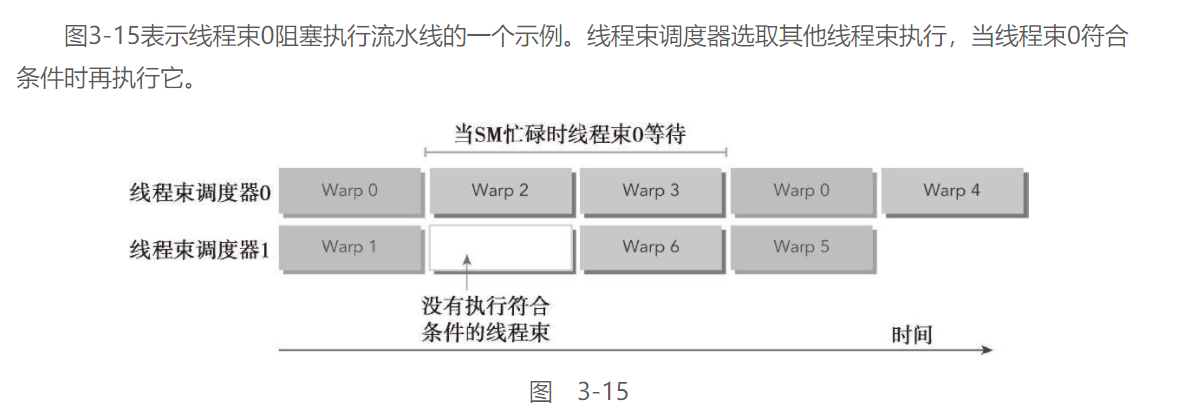
延时隐藏:

书里讲解的不是很详细, 可以看这里理解:

https://blog.csdn.net/fb_help/article/details/81707216

指令延时的定义:

在指令发出和完成之间的时钟周期被定义为指令延时

延时隐藏:

当每个时钟周期中, 所有的线程调度器都有一个符合条件的线程束时, 可以达到计算资源的完全利用, 此时, 通过其他常驻线程束中发布其他指令, 可以隐藏每个指令的延时

指令延时隐藏可以理解为流水线, 当有足够的常驻线程束供线程束调度器使用时, GPU就能在每个周期内的每一个流水线阶段中忙碌, GPU的指令延时被其他线程束的计算隐藏

指令分类:

根据指令延迟进行区分，指令可以被分为两种基本类型：

算术指令
算术指令延迟是一个算术操作从开始到它产生输出之间的时间

大约为10~20个周期
内存指令
存指令延迟是指发送出的加载或存储操作和数据到达目的地之间的时间

全局内存访问(显存)为400～800个周期

吞吐量 & 带宽:

这俩都是用来度量性能的速度指标

带宽:

带宽通常是指理论峰值, 用来描述单位时间内最大可能的数据传输量

吞吐量:

吞吐量是指已达到的值, 用来描述单位时间内任何形式的信息或操作的执行速度, 例如，每个周期完成多少个指令

估算延时隐藏需要的活跃线程束:

利特尔法则（Little’s Law）可以提供一个合理的近似值
$所需线程束数量＝延迟 \times 吞吐量$

这里的吞吐量一般指的是一组SM中CUDA核心的数量
如Kepler的一个SM中有192个CUDA核心, 即可得吞吐量为192线程, 折合6个线程束

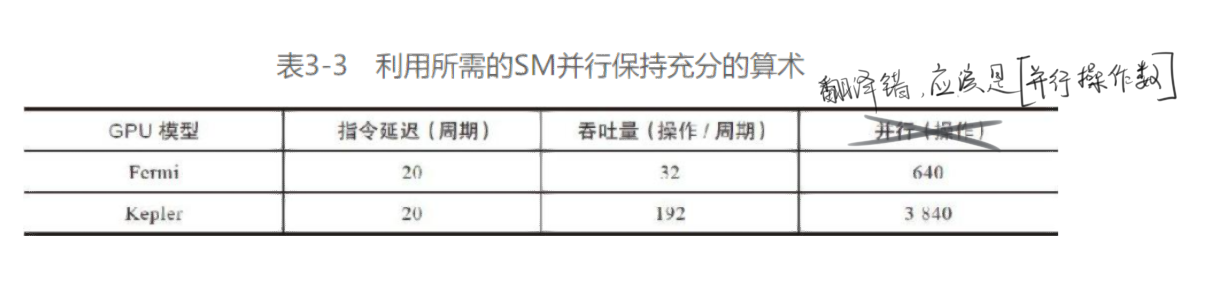
而利用上头的吞吐量& 带宽可以更有效的精确所需的活跃线程束:

这里引入一个概念: 并行 , 用于计算所需的活跃线程束

对于算数计算:

算数运算所需的并行可以表示成隐藏算术延迟所需要的操作数量

以32位的浮点数乘加运算（a＋b×c）为例:

表示在每个SM中每个时钟周期内的操作数量, 吞吐量因不同的算术指令而不同

算数运算所需的线程束数量基本与上头的Little’s Law相符合
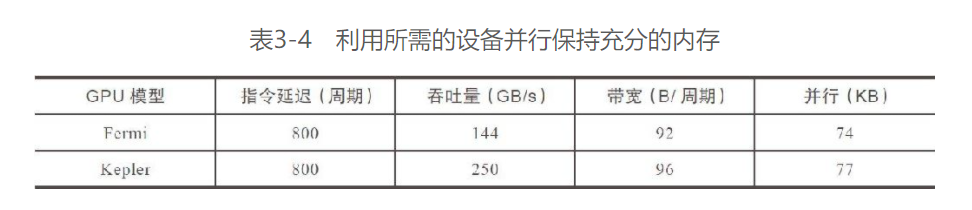
对于内存操作:

内存操作所需的并行可以表示为在每个周期内隐藏内存延迟所需的字节数

这里注意带宽的单位为 B/周期 , 而内存带宽的官方单位通常是MB/s 所以需要利用内存频率进行换算:

可得出:
$所需的并行字节量 = 指令延时 (周期) * 带宽 (字节 / 周期)$
由此就能计算出所需的活跃线程束数量:
$活跃线程数 = 所需的并行字节量 / 每线程占用的字节量$
以Fermi架构为例, 假设每个线程都把一浮点数据（4个字节）从全局内存移动到SM中用于计算

74 KB÷4字节/线程≈18500个线程

18500个线程÷32个线程/线程束≈579个线程束

由于内存带宽是全局的, 所以这里需要的线程束也是全局的

平均到每个SM单元上, 需要579个线程束÷16个SM＝36个线程束/SM

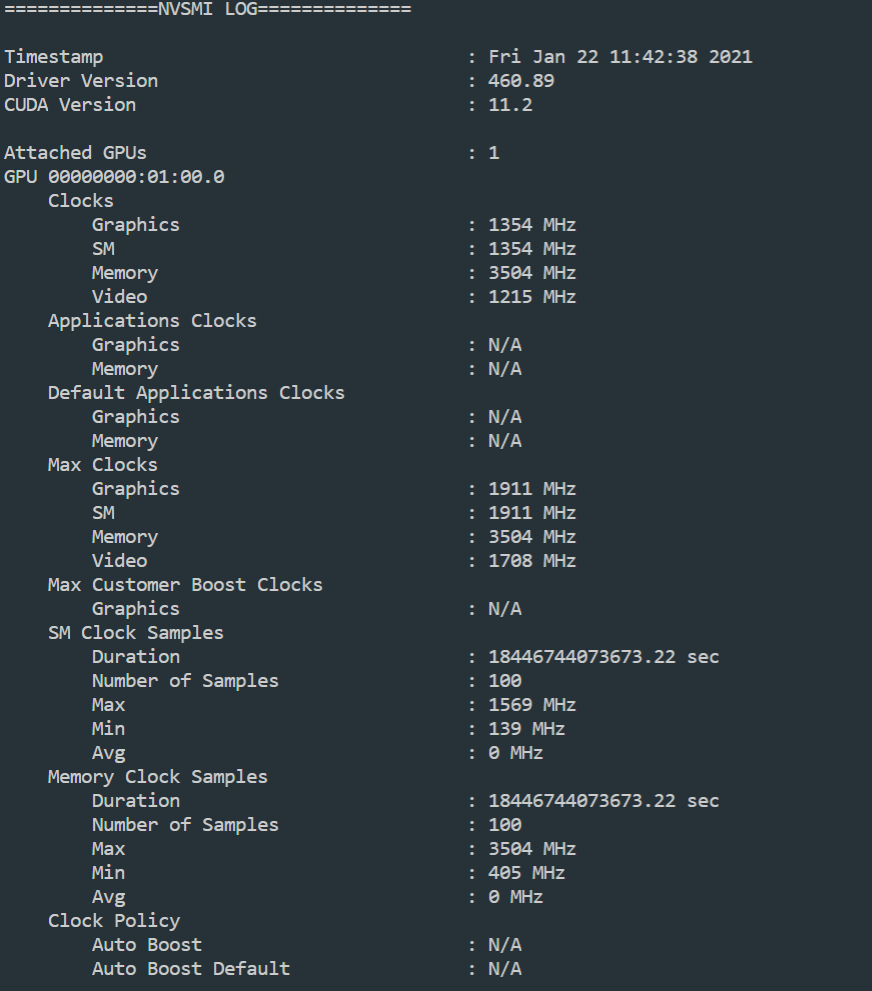
获取显卡最大内存频率的方法:

.\nvidia-smi.exe -a -q -d CLOCK

Max Clocks项中Memory即为内存最大频率

使用nvidia-smi查询最详尽的信息:

就不一个一个指令去学了, 这里直接输出所有的信息:

==============NVSMI LOG==============

Timestamp                                 : Fri Jan 22 11:51:09 2021
Driver Version                            : 460.89
CUDA Version                              : 11.2

Attached GPUs                             : 1
GPU 00000000:01:00.0
    Product Name                          : GeForce GTX 1050
    Product Brand                         : GeForce
    Display Mode                          : Enabled
    Display Active                        : Enabled
    Persistence Mode                      : N/A
    MIG Mode
        Current                           : N/A
        Pending                           : N/A
    Accounting Mode                       : Disabled
    Accounting Mode Buffer Size           : 4000
    Driver Model
        Current                           : WDDM
        Pending                           : WDDM
    Serial Number                         : N/A
    GPU UUID                              : GPU-e117532e-dc16-233b-a63e-bc3f7b5f58e4
    Minor Number                          : N/A
    VBIOS Version                         : 86.07.50.00.5A
    MultiGPU Board                        : No
    Board ID                              : 0x100
    GPU Part Number                       : N/A
    Inforom Version
        Image Version                     : N/A
        OEM Object                        : N/A
        ECC Object                        : N/A
        Power Management Object           : N/A
    GPU Operation Mode
        Current                           : N/A
        Pending                           : N/A
    GPU Virtualization Mode
        Virtualization Mode               : None
        Host VGPU Mode                    : N/A
    IBMNPU
        Relaxed Ordering Mode             : N/A
    PCI
        Bus                               : 0x01
        Device                            : 0x00
        Domain                            : 0x0000
        Device Id                         : 0x1C8D10DE
        Bus Id                            : 00000000:01:00.0
        Sub System Id                     : 0x852B1558
        GPU Link Info
            PCIe Generation
                Max                       : 3
                Current                   : 3
            Link Width
                Max                       : 16x
                Current                   : 8x
        Bridge Chip
            Type                          : N/A
            Firmware                      : N/A
        Replays Since Reset               : 0
        Replay Number Rollovers           : 0
        Tx Throughput                     : 4000 KB/s
        Rx Throughput                     : 5000 KB/s
    Fan Speed                             : N/A
    Performance State                     : P3
    Clocks Throttle Reasons
        Idle                              : Active
        Applications Clocks Setting       : Not Active
        SW Power Cap                      : Not Active
        HW Slowdown                       : Not Active
            HW Thermal Slowdown           : Not Active
            HW Power Brake Slowdown       : Not Active
        Sync Boost                        : Not Active
        SW Thermal Slowdown               : Not Active
        Display Clock Setting             : Not Active
    FB Memory Usage
        Total                             : 4096 MiB
        Used                              : 1629 MiB
        Free                              : 2467 MiB
    BAR1 Memory Usage
        Total                             : 256 MiB
        Used                              : 228 MiB
        Free                              : 28 MiB
    Compute Mode                          : Default
    Utilization
        Gpu                               : 15 %
        Memory                            : 8 %
        Encoder                           : 0 %
        Decoder                           : 0 %
    Encoder Stats
        Active Sessions                   : 0
        Average FPS                       : 0
        Average Latency                   : 0
    FBC Stats
        Active Sessions                   : 0
        Average FPS                       : 0
        Average Latency                   : 0
    Ecc Mode
        Current                           : N/A
        Pending                           : N/A
    ECC Errors
        Volatile
            Single Bit
                Device Memory             : N/A
                Register File             : N/A
                L1 Cache                  : N/A
                L2 Cache                  : N/A
                Texture Memory            : N/A
                Texture Shared            : N/A
                CBU                       : N/A
                Total                     : N/A
            Double Bit
                Device Memory             : N/A
                Register File             : N/A
                L1 Cache                  : N/A
                L2 Cache                  : N/A
                Texture Memory            : N/A
                Texture Shared            : N/A
                CBU                       : N/A
                Total                     : N/A
        Aggregate
            Single Bit
                Device Memory             : N/A
                Register File             : N/A
                L1 Cache                  : N/A
                L2 Cache                  : N/A
                Texture Memory            : N/A
                Texture Shared            : N/A
                CBU                       : N/A
                Total                     : N/A
            Double Bit
                Device Memory             : N/A
                Register File             : N/A
                L1 Cache                  : N/A
                L2 Cache                  : N/A
                Texture Memory            : N/A
                Texture Shared            : N/A
                CBU                       : N/A
                Total                     : N/A
    Retired Pages
        Single Bit ECC                    : N/A
        Double Bit ECC                    : N/A
        Pending Page Blacklist            : N/A
    Remapped Rows                         : N/A
    Temperature
        GPU Current Temp                  : 46 C
        GPU Shutdown Temp                 : 102 C
        GPU Slowdown Temp                 : 97 C
        GPU Max Operating Temp            : 94 C
        GPU Target Temperature            : N/A
        Memory Current Temp               : N/A
        Memory Max Operating Temp         : N/A
    Power Readings
        Power Management                  : N/A
        Power Draw                        : N/A
        Power Limit                       : N/A
        Default Power Limit               : N/A
        Enforced Power Limit              : N/A
        Min Power Limit                   : N/A
        Max Power Limit                   : N/A
    Clocks
        Graphics                          : 683 MHz
        SM                                : 683 MHz
        Memory                            : 2504 MHz
        Video                             : 607 MHz
    Applications Clocks
        Graphics                          : N/A
        Memory                            : N/A
    Default Applications Clocks
        Graphics                          : N/A
        Memory                            : N/A
    Max Clocks
        Graphics                          : 1911 MHz
        SM                                : 1911 MHz
        Memory                            : 3504 MHz
        Video                             : 1708 MHz
    Max Customer Boost Clocks
        Graphics                          : N/A
    Clock Policy
        Auto Boost                        : N/A
        Auto Boost Default                : N/A


后头是一些应用占用显卡资源的信息, 本文忽略

由此计算GTX1050所需的活跃线程束数量:

对于内存操作: 每个SM需要至少41个线程束才能吃满

对于算数操作: 每个SM需要至少2560个线程折合80个线程束才能吃满

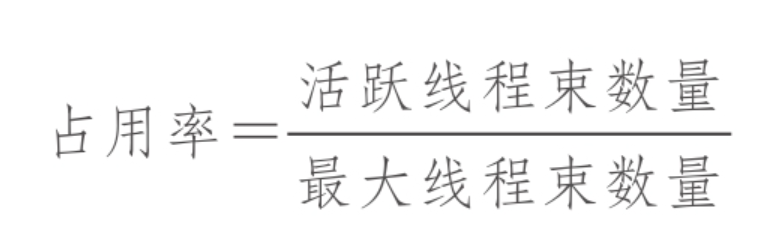
占用率:

占用率计算公式:

其中最大线程数量使用上一章的prop.maxThreadsPerMultiProcessor可以获取

对于GTX1050:

占用率最大化:

本部分CUDA_Occupancy_Calculator的使用不是很明确, 也就会填个参数, 其余的指标不知道有啥用

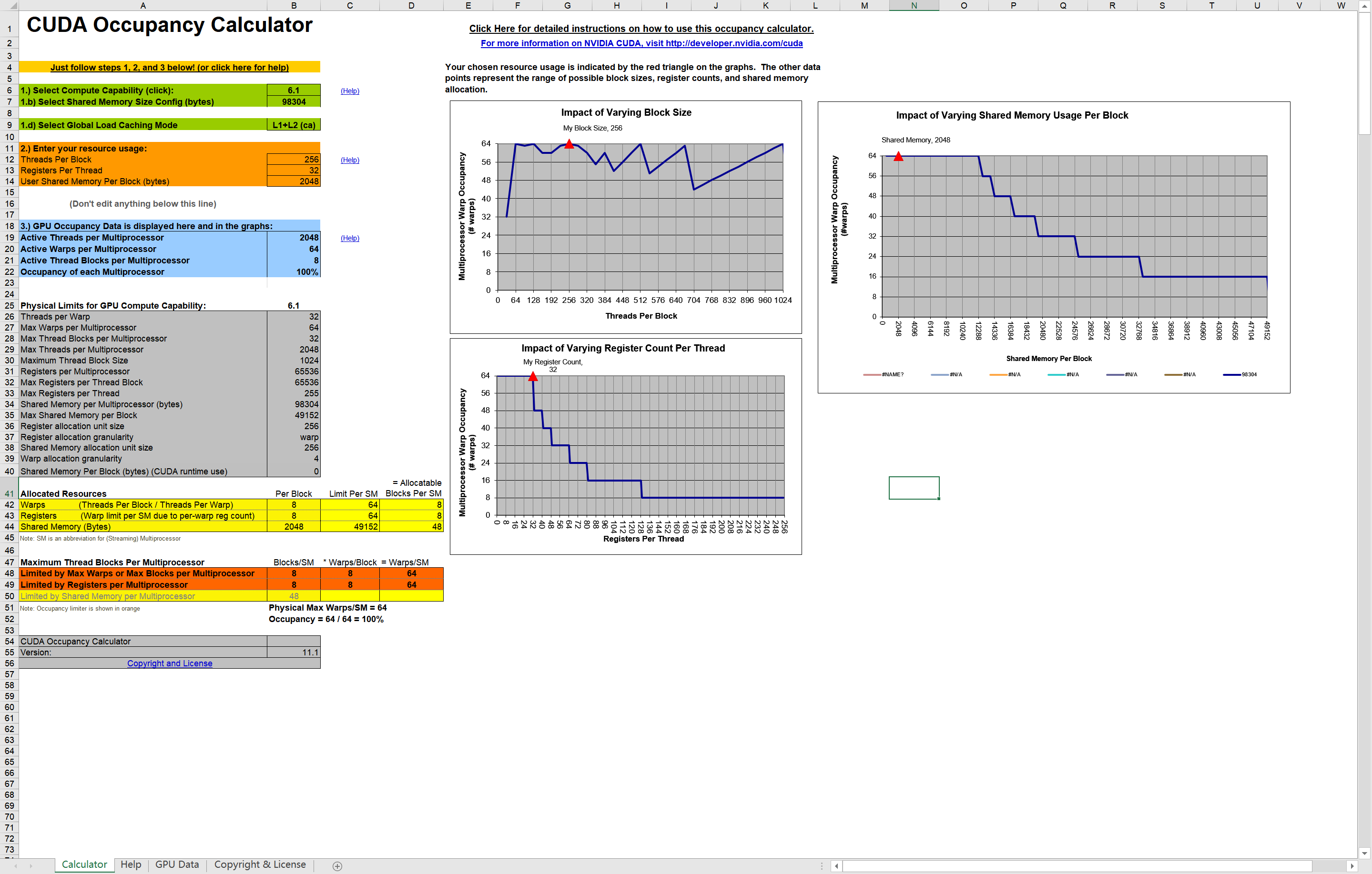
CUDA_ToolKit中提供了一个excel计算器, 输入必要的参数之后能够帮助我们确定网络和快的维数以使一个内核占用率最大化

根据界面上的使用教程, 仅需填入最上方的三个部分, 即可生成关键数据:

现在只需要填入关键信息:

GPU计算能力
Select Compute Capability (click)

这个通过deviceQuery查询可得到:

Device 0: "GeForce GTX 1050"
  CUDA Driver Version / Runtime Version          11.2 / 11.2
  CUDA Capability Major/Minor version number:    6.1

共享内存配置
Select Shared Memory Size Config (bytes)

本部分也是使用deviceQuery得到:

  Total amount of constant memory:               65536 bytes
  Total amount of shared memory per block:       49152 bytes
  Total shared memory per multiprocessor:        98304 bytes

每个块的线程
Threads Per Block

这部分是代码中的核函数执行配置

每个线程的寄存器
Registers Per Thread

后头这俩通过nvcc得到, 添加如下参数:

nvcc -arch sm_61 --ptxas-options=-v .\cuda_test.cu -o cuda_test.exe

-arch sm_61指定使用Pascal架构编译
--ptxas-options=-v 这部分指定其统计这俩的量:

输出结果:

PS D:\NVIDIA_CUDA\CUDA_Project\VScode_CUDA_Project> nvcc -arch sm_61 --ptxas-options=-v .\cuda_test.cu -o cuda_test.exe         
./cuda_test.cu: warning C4819: 该文件包含不能在当前代码页(936)中表示的字符。请将该文件保存为 Unicode 格式以防止数据丢失
./cuda_test.cu(156): warning: variable "threadNum" was declared but never referenced

ptxas info    : 0 bytes gmem
ptxas info    : Compiling entry function '_Z13sumArrayOnGPUPfS_S_ii' for 'sm_61'
ptxas info    : Function properties for _Z13sumArrayOnGPUPfS_S_ii
    0 bytes stack frame, 0 bytes spill stores, 0 bytes spill loads
ptxas info    : Used 11 registers, 352 bytes cmem[0]
./cuda_test.cu: warning C4819: 该文件包含不能在当前代码页(936)中表示的字符。请将该文件保存为 Unicode 格式以防止数据丢失
  正在创建库 cuda_test.lib 和对象 cuda_test.exp

每个块的共享内存:
User Shared Memory Per Block (bytes)

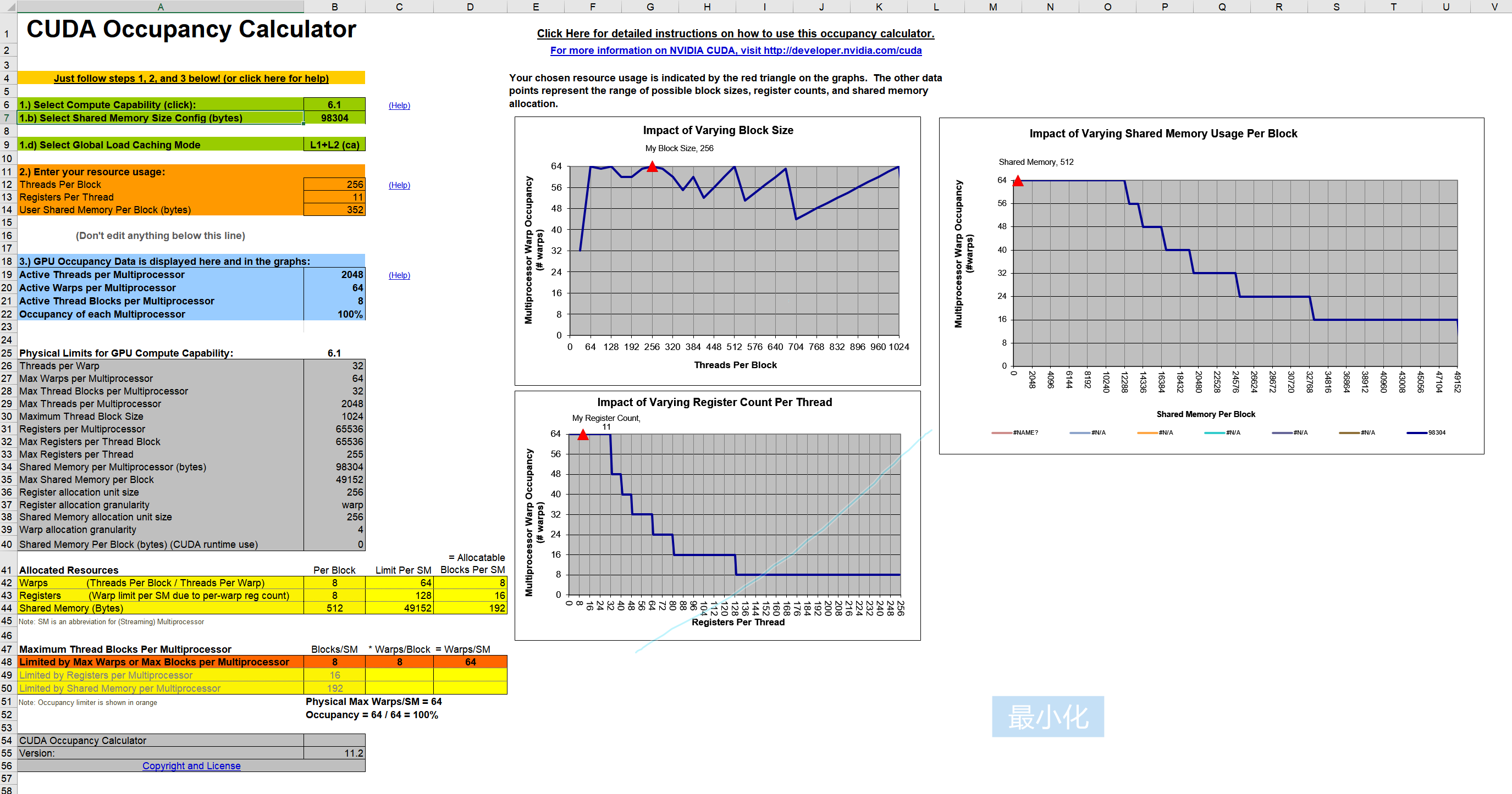
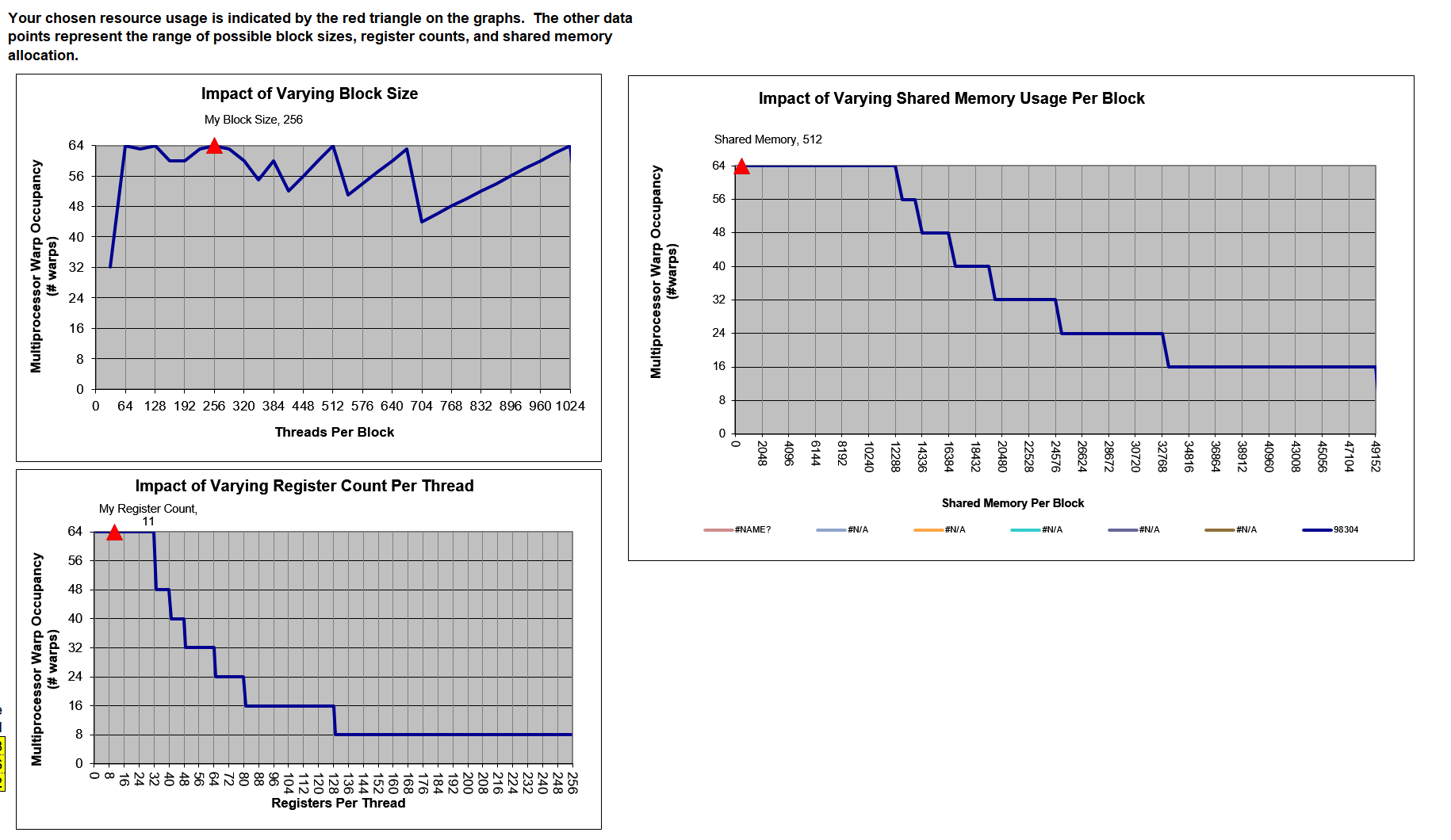
最终结果:

蓝色框这里输出的就是当前配置所得到的占用率:

这三个表格表示配置不同导致的占用率变化:

网格和线程块大小的准则:

小线程块：每个块中线程太少，会在所有资源被充分利用之前导致硬件达到每个SM的线程束数量的限制。
大线程块：每个块中有太多的线程，会导致在每个SM中每个线程可用的硬件资源较少。

所以需要:

保持每个块中线程数量是线程束大小（32）的倍数
避免块太小：每个块至少要有128或256个线程
根据内核资源的需求调整块大小
块的数量要远远多于SM的数量，从而在设备中可以显示有足够的并行
通过实验得到最佳执行配置和资源使用情况

同步:

栅栏同步(barrier synchronize) 在很多并行编程语言中都很常见(如MPI)

在CUDA中, 同步可以在两个级别执行:

系统级：等待主机和设备完成所有的工作
块级：在设备执行过程中等待一个线程块中所有线程到达同一点

对于主机而言, 之前已经使用过一个同步函数:

对于设备而言, 使用以下:

当调用时, 在同一个线程块中的每个线程会进行一次强制同步, 需要注意的是, 已经到达barrier的线程需要等待块中其余能够到达同一个barrier的线程, 而非是块中的所有线程

在栅栏之前所有线程产生的所有全局内存和共享内存访问，将会在栅栏后对线程块中所有其他的线程可见

注意: 不同块之间是没有线程同步的, 因此, GPU可以以任意的顺序执行块

块间同步, 唯一安全的方法是在每个内核执行结束端使用全局同步点

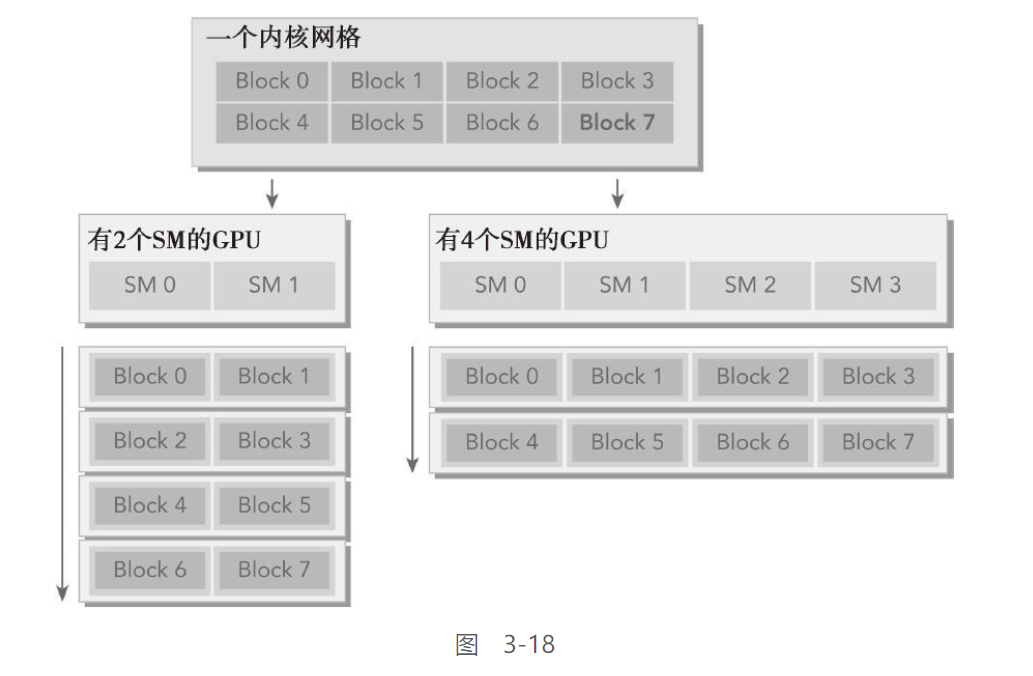
可扩展性:

这里的可扩展性的概念基本上与MPI中的概念相同:

一个可扩展但效率很低的系统可以通过简单添加硬件核心来处理更大的工作负载。一个效率很高但不可扩展的系统可能很快会达到可实现性能的上限。

3.3 并行性的表现:

本节部分将利用不同的执行配置分析矩阵加法, 理解线程束执行的本质

矩阵加法仍然使用之前的版本:

//这里默认使用二维grid, 二维block
//需要将整个grid映射到数组中
__global__ void sumArrayOnGPU(float *a, float *b, float *c, const int nx, const int ny)
{
    unsigned long size = nx * ny; //数据集总数
    //这里将二维的线程组转化为一维线程组进行计算
    unsigned long threadNum = gridDim.x * gridDim.y * blockDim.x * blockDim.y; //线程组总数
    unsigned long ix = threadIdx.x + blockIdx.x * blockDim.x;                  //线程在线程组中的(x,y)编号
    unsigned long iy = threadIdx.y + blockIdx.y * blockDim.y;
    unsigned long tid = iy * blockDim.x * gridDim.x + ix; //线程在线程组中的顺序编号

    //执行计算
    for (unsigned long i = tid; i < size; i += threadNum)
    {
        c[i] = a[i] + b[i];
    }
    // // int i= threadIdx.x;
    // for (int i = threadIdx.x * (blockIdx.x + 1); i < N; i += blockDim.x)
    // {
    //     c[i] = a[i] + b[i];
    // }
    return;
}

例程:

#include <cuda_runtime.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

#define CHECK(call) { \
    const cudaError_t error = call;\
    if (error != cudaSuccess)\
    {\
        printf("Error: %s:%d\n", __FILE__, __LINE__);\
        printf("code: %d, reason: %s\n", error, cudaGetErrorString(error));\
        exit(1);\
    }\
} 

void checkResult(float *cpuAns, float *gpuAns, const int nx, const int ny)
{
    unsigned long size = nx * ny;
    for (unsigned long i = 0; i < size; ++i)
    {
        if (cpuAns[i] != gpuAns[i])
        {
            unsigned long tempI = size / nx;
            unsigned long tempJ = i - (i * nx);
            printf(
                "Error!\n"
                "On i=%u , j=%u \n"
                "CPU_ans = %.4lf\n"
                "GPU_ans = %.4lf\n",
                tempI, tempJ, cpuAns[i], gpuAns[i]);
            break ;
        }
    }
}

void sumArrayOnCPU(float *A, float *B, float *C, const int nx, const int ny)
{
    unsigned long size = nx * ny;
    for (unsigned long i = 0; i < size; ++i)
    {
        C[i] = A[i] + B[i];
    }
    return;
}

void initData(float *data, unsigned long size)
{

    for (unsigned long i = 0; i < size; ++i)
    {
        data[i] = (float)(rand() & 0xFF) / 100.0f;
    }

    return;
}

//这里默认使用二维grid, 二维block
//需要将整个grid映射到数组中
__global__ void sumArrayOnGPU(float *a, float *b, float *c, const int nx, const int ny)
{
    unsigned long size = nx * ny; //数据集总数
    //这里将二维的线程组转化为一维线程组进行计算
    unsigned long threadNum = gridDim.x * gridDim.y * blockDim.x * blockDim.y; //线程组总数
    unsigned long ix = threadIdx.x + blockIdx.x * blockDim.x;                  //线程在线程组中的(x,y)编号
    unsigned long iy = threadIdx.y + blockIdx.y * blockDim.y;
    unsigned long tid = iy * blockDim.x * gridDim.x + ix; //线程在线程组中的顺序编号

    //执行计算
    for (unsigned long i = tid; i < size; i += threadNum)
    {
        c[i] = a[i] + b[i];
    }
    return;
}

int main()
{

    srand(time(0));

    printf("Start calculating.....\n");

    // int elemNum = 640 * 10000;
    const int nx = 1 << 14, ny = 1 << 14;
    const unsigned long elemNum = nx * ny;
    printf("Matrix size = %d * %d\n", ny, nx);

    float *h_a = NULL;
    float *h_b = NULL;
    float *h_c = NULL;
    float *h_deviceC = NULL;
    h_a = (float *)calloc(elemNum, sizeof(float));
    h_b = (float *)calloc(elemNum, sizeof(float));
    h_c = (float *)calloc(elemNum, sizeof(float));
    h_deviceC = (float *)calloc(elemNum, sizeof(float));

    float *d_a = NULL, *d_b = NULL, *d_c = NULL;
    CHECK(cudaMalloc((float **)&d_a, elemNum * sizeof(float)));
    CHECK(cudaMalloc((float **)&d_b, elemNum * sizeof(float)));
    CHECK(cudaMalloc((float **)&d_c, elemNum * sizeof(float)));

    //初始化数据
    initData(h_a, elemNum);
    initData(h_b, elemNum);
    cudaMemcpy(d_a, h_a, elemNum * sizeof(float), cudaMemcpyHostToDevice);
    cudaMemcpy(d_b, h_b, elemNum * sizeof(float), cudaMemcpyHostToDevice);

    int threadNum = 12800; //CUDA_num=640, 这里开到2倍
    //block & grid 均分threadNum
    //1280质因数分解: 2*2*2*2*2*2*2*2*5
    dim3 block(16, 64, 1);
    dim3 grid(5, 5, 1);

    int startTime = clock();
    sumArrayOnGPU<<<grid, block>>>(d_a, d_b, d_c, nx, ny);
    cudaDeviceSynchronize();
    printf("执行配置: <<<%d, %d, %d>>> <<<%d, %d, %d>>>\n", grid.x, grid.y, grid.z, block.x, block.y, block.z);
    printf("GPU计算完成, 耗时%d ms \n", clock() - startTime);

    startTime = clock();
    sumArrayOnCPU(h_a, h_b, h_c, nx, ny);
    printf("CPU计算完成, 耗时%d ms \n", clock() - startTime);

    cudaMemcpy(h_deviceC, d_c, elemNum * sizeof(float), cudaMemcpyDeviceToHost);

    checkResult(h_c, h_deviceC, nx, ny);

    cudaFree(d_a);
    cudaFree(d_b);
    cudaFree(d_c);

    free(h_a);
    free(h_b);
    free(h_c);
    free(h_deviceC);

    return 0;
}

运行结果:

这里为了保证结果准确, 对每个执行配置都运行两次, 取最小值

Start calculating.....
Matrix size = 16384 * 16384
执行配置: <<<5, 5, 1>>> <<<32, 32, 1>>>
GPU计算完成, 耗时42 ms
CPU计算完成, 耗时986 ms

Start calculating.....
Matrix size = 16384 * 16384
执行配置: <<<5, 5, 1>>> <<<64, 16, 1>>>
GPU计算完成, 耗时36 ms
CPU计算完成, 耗时966 ms  

Start calculating.....
Matrix size = 16384 * 16384
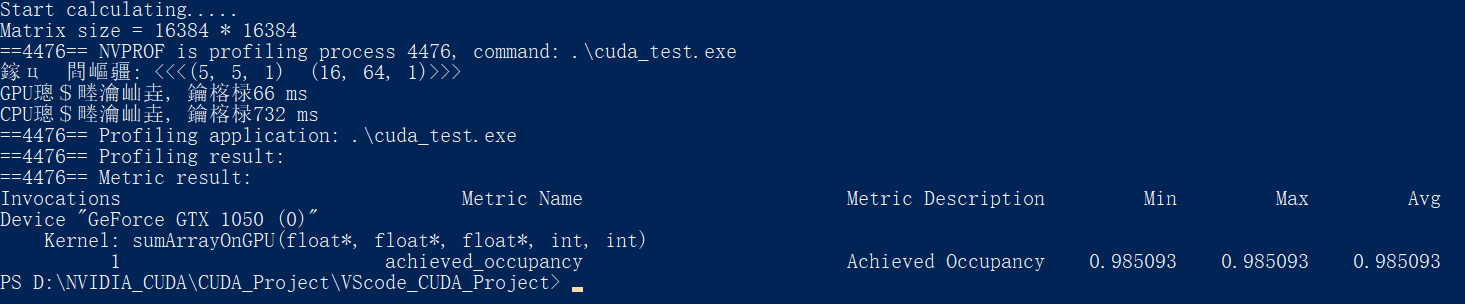
执行配置: <<<5, 5, 1>>> <<<16, 64, 1>>>
GPU计算完成, 耗时55 ms
CPU计算完成, 耗时1006 ms 

Start calculating.....
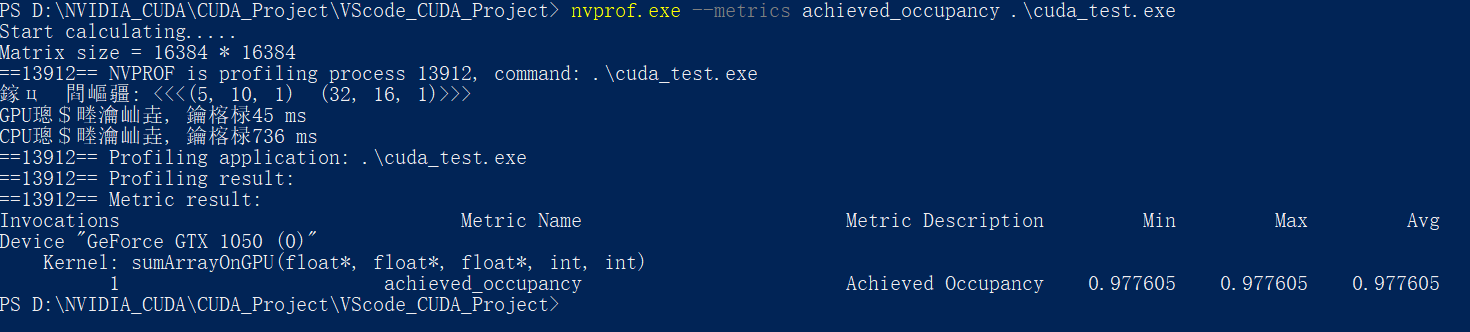
Matrix size = 16384 * 16384
执行配置: <<<5, 10, 1>>> <<<32, 16, 1>>>
GPU计算完成, 耗时36 ms
CPU计算完成, 耗时945 ms
    
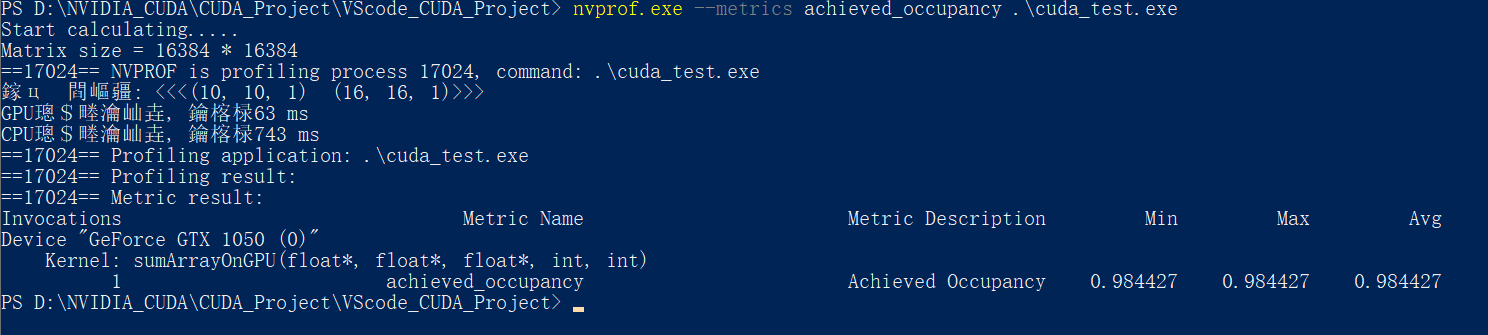
Start calculating.....
Matrix size = 16384 * 16384
执行配置: <<<10, 10, 1>>> <<<16, 16, 1>>>
GPU计算完成, 耗时53 ms
CPU计算完成, 耗时878 ms
    
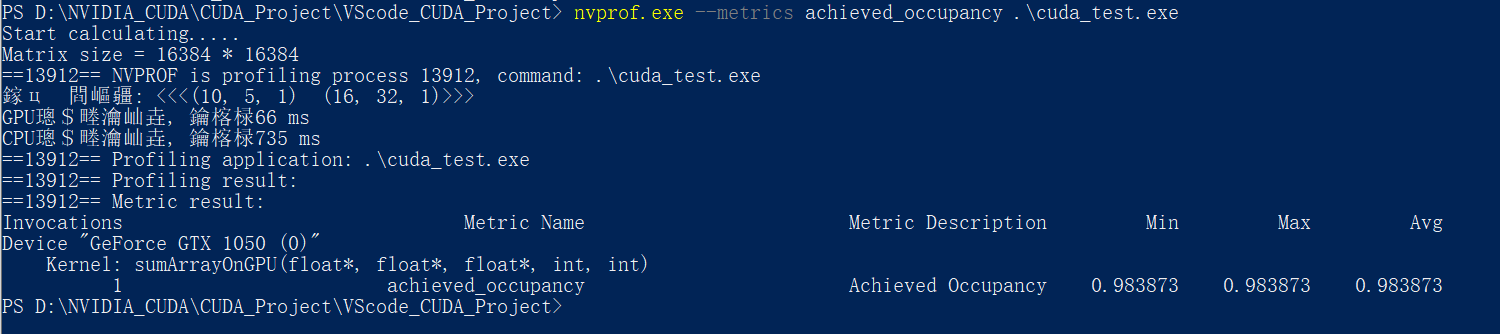
Start calculating.....
Matrix size = 16384 * 16384
执行配置: <<<10, 5, 1>>> <<<16, 32, 1>>>
GPU计算完成, 耗时54 ms
CPU计算完成, 耗时916 ms

使用nvprof检测相应的执行指标:

这里作死直接上--metrics all来获取所有的指标, 结果如下:

其会将数据暂存在C盘, 这里为了阅读方便, 直接使用截图:

所以, 之后想要获取某个单独的指令, 就直接加上相应的参数即可, 就上头的Metrics Name

使用nvprof检测活跃的线程束:

$内核可实现的占用率=\frac{每周期内活跃的线程束平均数量}{一个SM支持的线程束最大数量}$

nvprof中的内核占用率为上头的achieved_occupancy, 加上参数即可单独访问

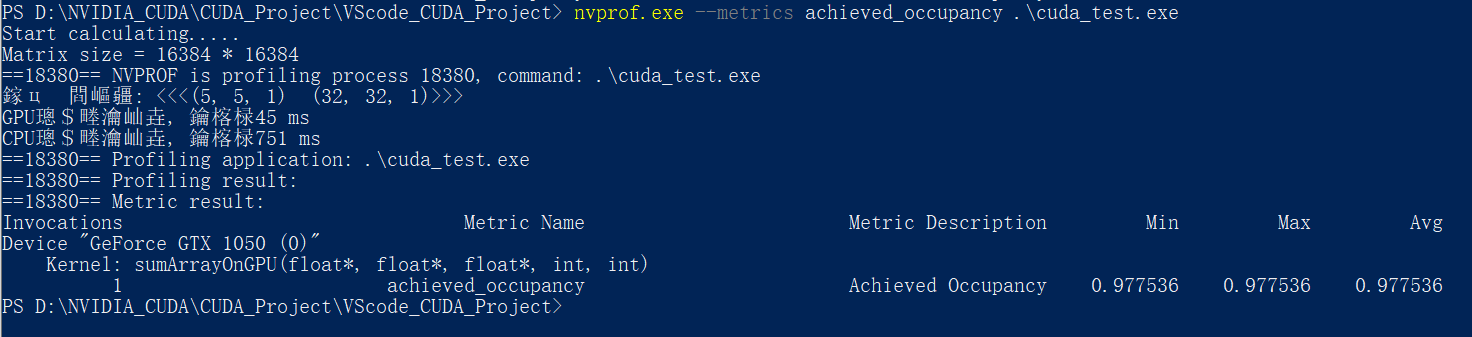
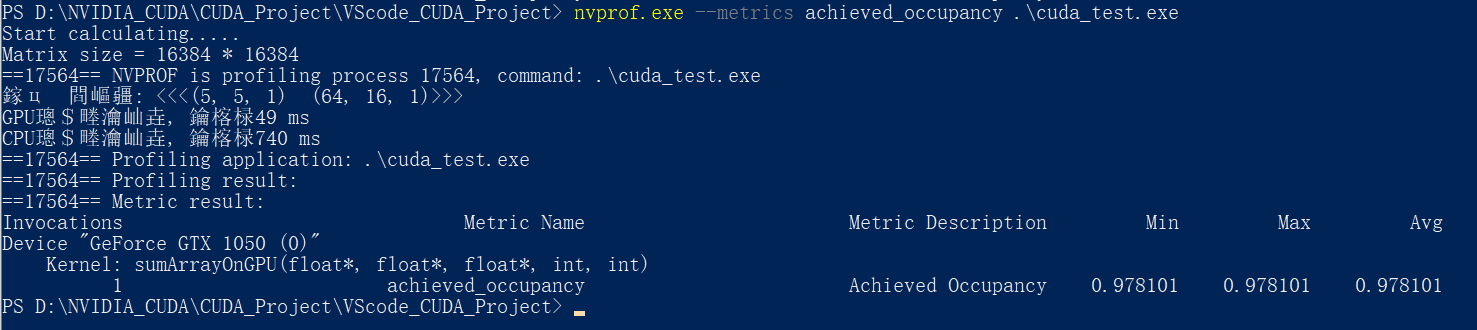
nvprof.exe --metrics achieved_occupancy .\cuda_test.exe

对于例程中的6种情况:

可以看到, 第三种配置<<<5, 5, 1>>> <<<16, 64, 1>>>的内核可实现占用率是最高的, 但是其计算速度并不是最快的
计算速度最快的反而是第一种<<<5, 5, 1>>> <<<32, 32, 1>>>与第四种<<<5, 10, 1>>> <<<32, 16, 1>>>配置

因此，更高的占用率并不一定意味着有更高的性能。肯定有其他因素限制GPU的性能

可实现占用率只能大致反应计算速度

用nvprof检测内存操作:

内存全局加载吞吐量:

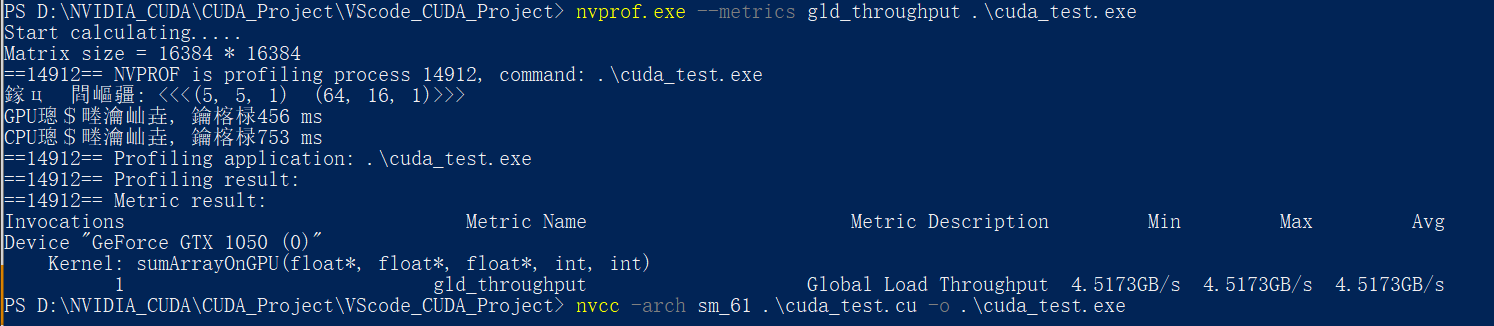
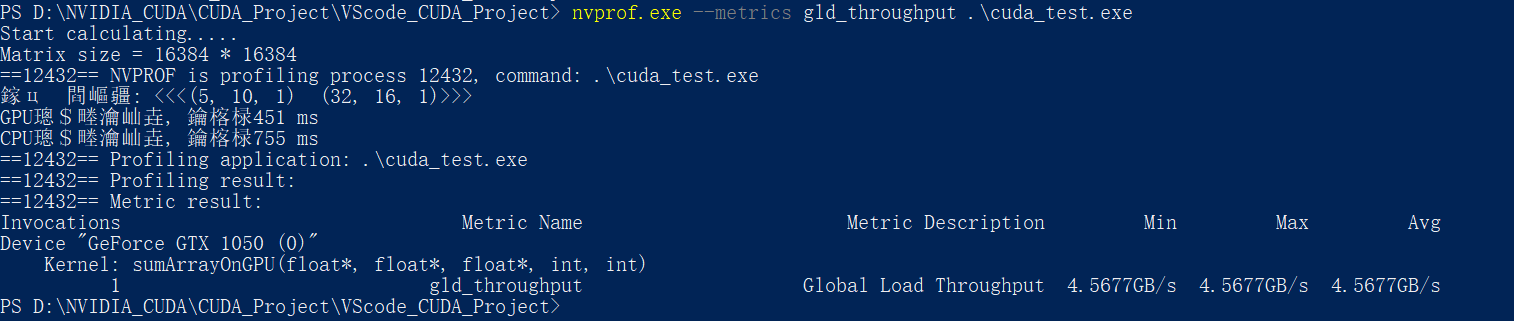
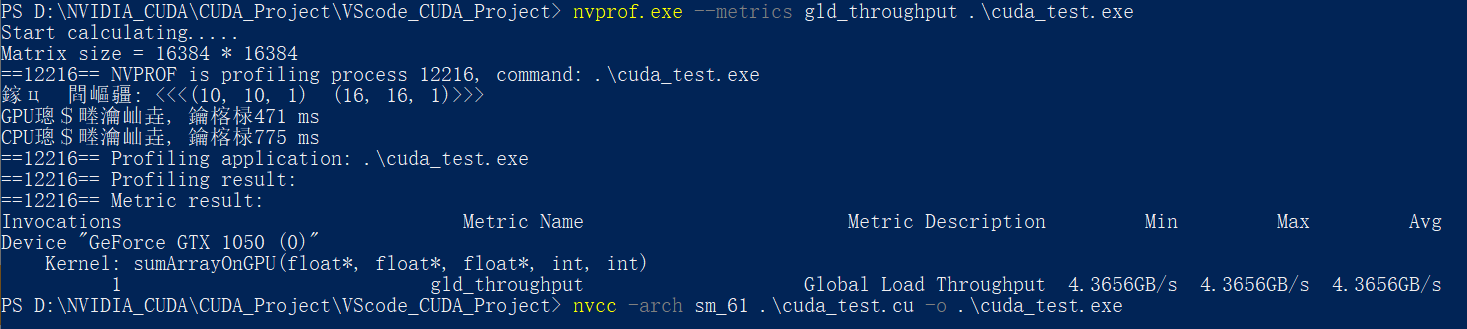
同样使用nvprof的–-metrics 指令+gld_throughput参数检测内存的全局加载吞吐量:

nvprof.exe --metrics gld_throughput .\cuda_test.exe

这里不知道为啥, 显存吞吐量很低

可以看到第四种<<<5, 10, 1>>> <<<32, 16, 1>>>执行配置的内存访问带宽最高, 同样对应的执行速度最快

但更高的读取效率并不一定意味着更高的性能

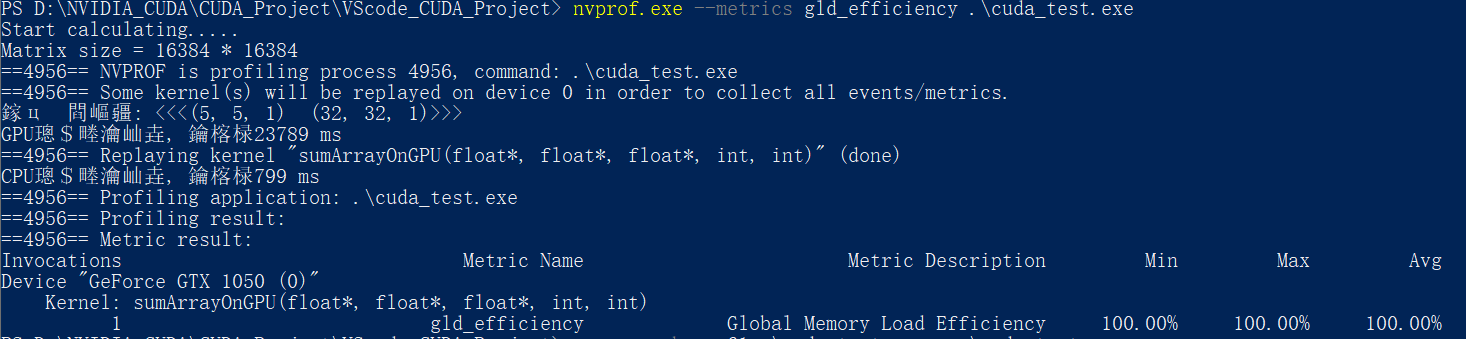
内存读取效率:

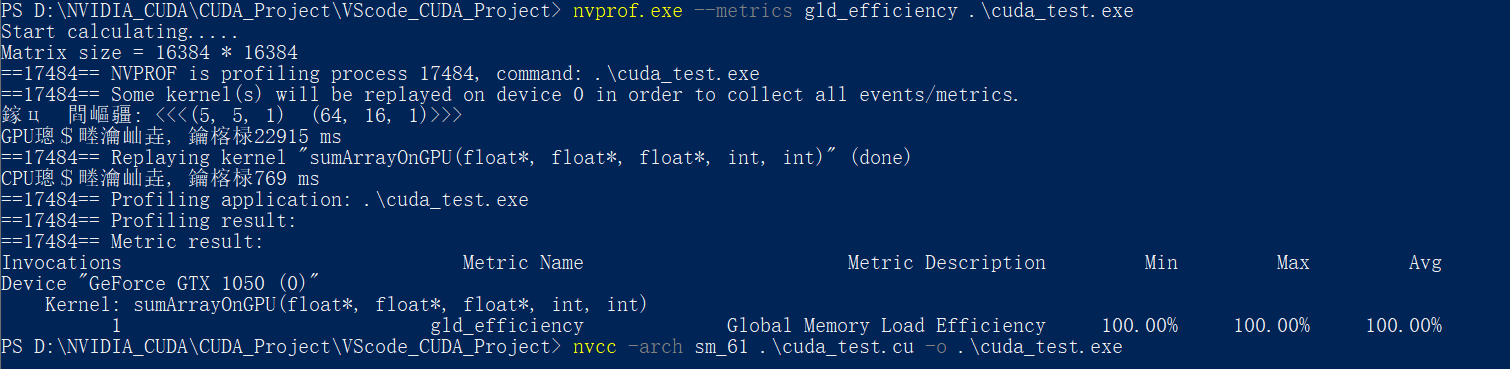
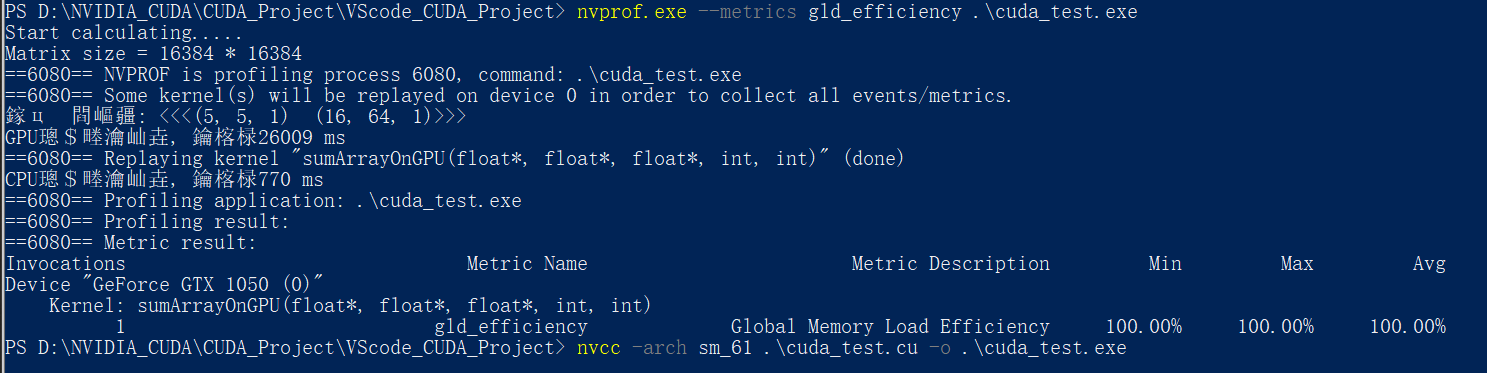
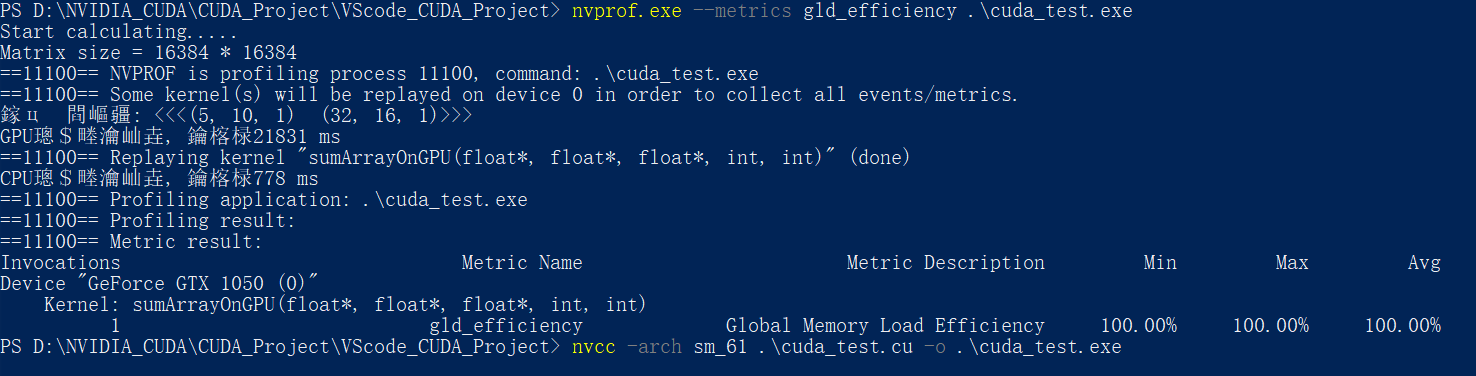
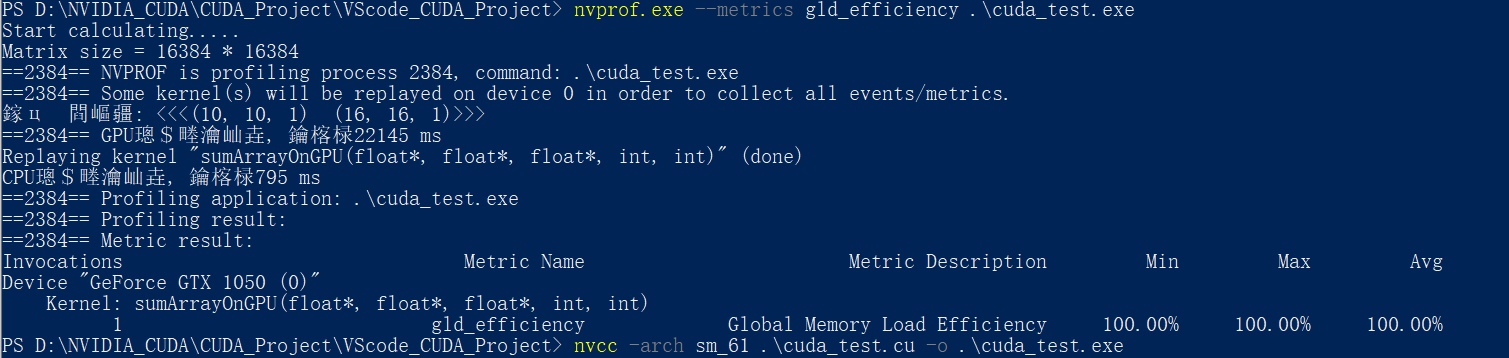
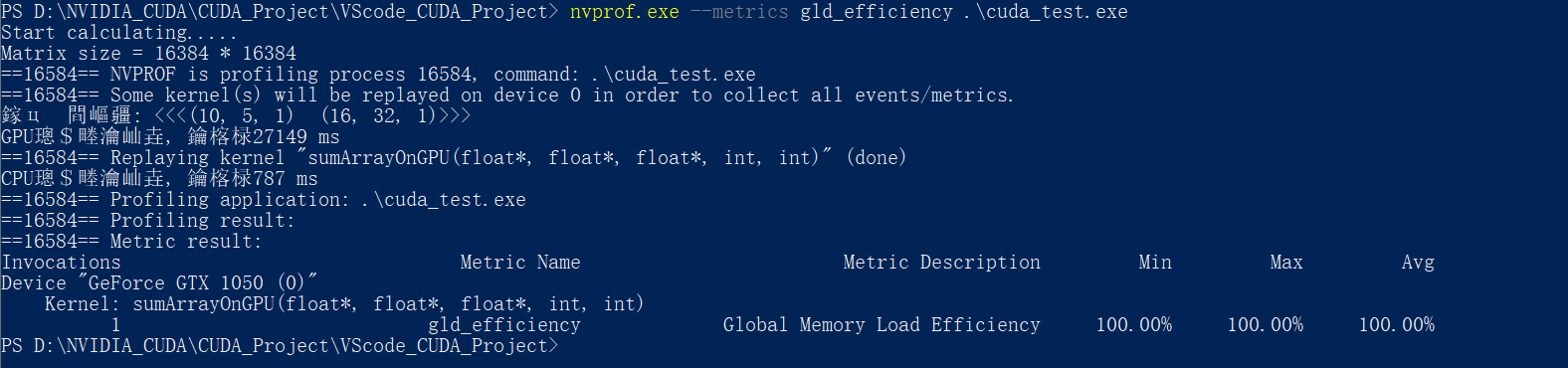
使用nvprof的–-metrics 指令+gld_efficiency参数检测内存的读取效率:

这里的6种执行配置的全局加载效率全为100% , 没有实现很好的对比

所以这里引用书里的图:

注意，最后两种情况的共同特征是它们在最内层维数中块的大小是线程束的一半。如前所述，对网格和块启发式算法来说，最内层的维数应该总是线程束大小的倍数。第4章将讨论半个线程束大小的线程块是如何影响性能的。

增大并行性:

本部分直接用书里的例子:

最好的结果是第四种情况，块大小为（128，2）

第一种情况中块大小为（64，2），尽管在这种情况下启动的线程块最多，但不是最快的配置
对比第二种与第四种配置:

其启动的的线程块数量相同, 在设备上表现出相同的并行性, 但第二种仍然比第四种性能要差, 所以:

线程块最内层维度的大小对性能起着的关键的作用
对比于其他几种配置:

线程块的数量都比最好的情况少, 所以:

增大并行性仍然是性能优化的一个重要因素

占用率对比:

占用率最高的为第四种配置, 这与上头的结论相同

第一种情况 (64,2)的块大小最小, 能够得到最多的线程块, 但是其在所有例子中的占用率最低
此为线程块的最大数量遇到了硬件限制
对比第四种(128,2) 与第七种(256,2):

其执行时间相近, 基本上可以算是同一性能水平

在block.y=1的情况下, 实现了最好性能:

此时的占用率, 加载吞吐量&加载效率:

总结:

在大部分情况下，一个单独的指标不能产生最佳的性能
与总体性能最直接相关的指标或事件取决于内核代码的本质
在相关的指标与事件之间寻求一个好的平衡
从不同角度查看内核以寻找相关指标间的平衡
网格/块启发式算法为性能调节提供了一个很好的起点

3.4 避免分支分化

本节介绍并行归约

并行归约问题:

归约问题在MPI的学习中已经有所接触了

在向量中执行满足交换律和结合律的运算，被称为归约问题。并行归约问题是这种运算的并行执行。并行归约是一种最常见的并行模式，并且是许多并行算法中的一个关键运算。

针对于并行矩阵加法问题:

将输入向量划分到更小的数据块中。
用一个线程计算一个数据块的部分和。
对每个数据块的部分和再求和得出最终结果。

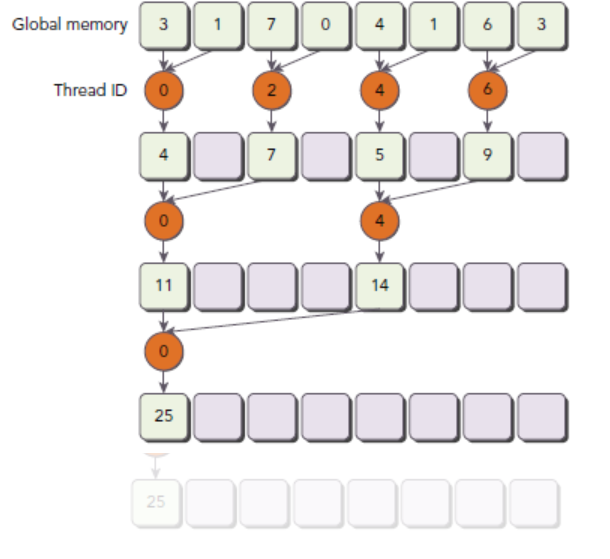
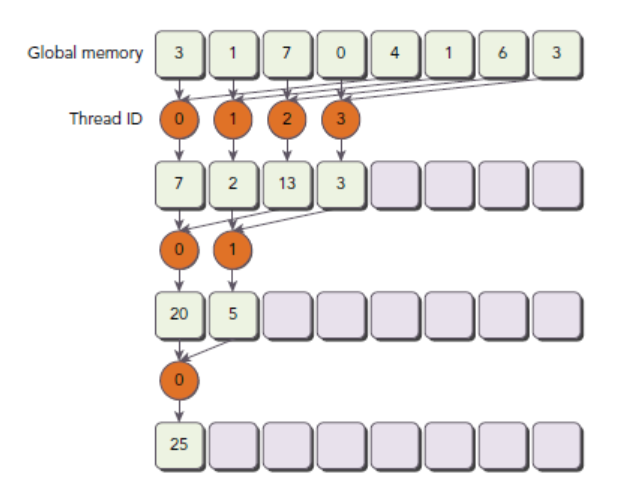
书中采用的方法为类似归并排序的方法:

相邻配对：元素与它们直接相邻的元素配对
交错配对：根据给定的跨度配对元素

按照这个归约策略, 可以尽可能的减少串行求和的占比
在GPU中, 单核性能远没有CPU单核来得快, 所以尽可能的减少串行占比是很有必要的, 这也是CPU并行策略与GPU并行策略不同的原因

CPU代码实现如下 (交错配对) :

并行归约中的分化

按照图中的归约策略, 有如下核函数:

这是书里的核函数, 有问题的版本, idx没定义…….
所以这部分就不进行手写了, 因为性能实在是糟糕, 直接跳到下头的改进版本

__global__ void reduceNeighbored(int *g_idata, int *g_odata, unsigned int n) {
    // set thread ID
    unsigned int tid = threadIdx.x;
    // convert global data pointer to the local pointer of this block
    int *idata = g_idata + blockIdx.x * blockDim.x;
    // boundary check
    if (idx >= n) return;
        // in-place reduction in global memory
    for (int stride = 1; stride < blockDim.x; stride *= 2) {
        if ((tid % (2 * stride)) == 0) {
            idata[tid] += idata[tid + stride];
        }
        // synchronize within block
        __syncthreads();
    }
    // write result for this block to global mem
    if (tid == 0) g_odata[blockIdx.x] = idata[0];
}

由于线程块间无法同步, 所以每个线程块产生的部分和被复制回主机进行串行求和

后序可再次启动核函数进行进一步的串行求和

改善并行归约的分化

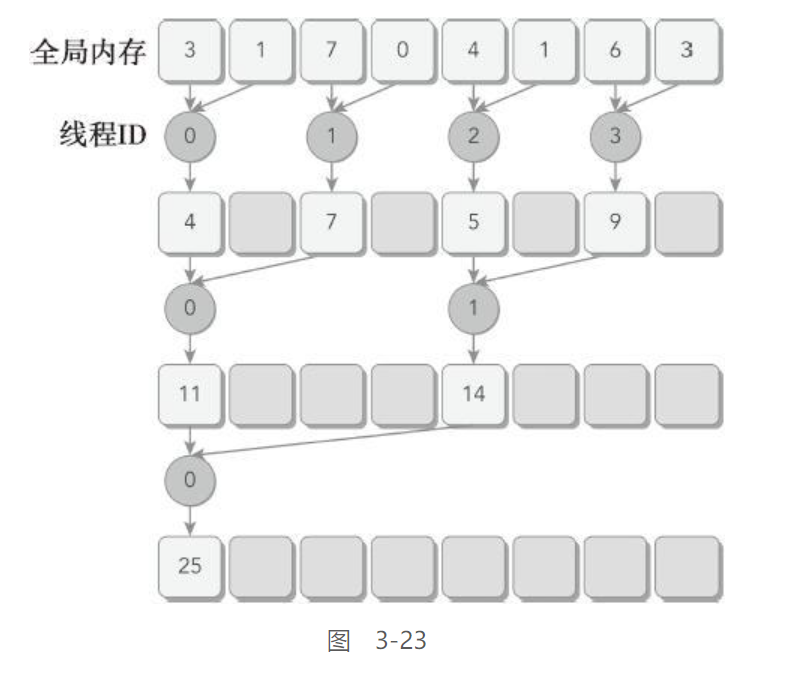
这里改善的主要是上头样例代码中的线程束分化问题

其犯了个很明显的错误, 在同一个线程束中使用了奇偶线程交错的形式, 这在归约过程中将产生大量的分支, 使得并行效率下降

所以将归约策略修正如下:

不在使用间隔的tid进行计算, 而是使用连续的tid进行计算
但在最后5次归约中, 由于线程量的不足, 还是会出现线程束分化的问题, 这是无法避免的

__global__ void reduceNeighboredLess (int *g_idata, int *g_odata, unsigned int n) {
    // set thread ID
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;
    // convert global data pointer to the local pointer of this block
    int *idata = g_idata + blockIdx.x*blockDim.x;
    // boundary check
    if(idx >= n) return;
    // in-place reduction in global memory
    for (int stride = 1; stride < blockDim.x; stride *= 2) {
        // convert tid into local array index
        int index = 2 * stride * tid;
        if (index < blockDim.x) {
            idata[index] += idata[index + stride];
        }    
        // synchronize within threadblock
        __syncthreads();
    }
    // write result for this block to global mem
    if (tid == 0) g_odata[blockIdx.x] = idata[0];
}

交错配对的归约

与相邻配对方法相比，交错配对方法颠倒了元素的跨度
初始跨度是线程块大小的一半，然后在每次迭代中减少一半

核函数如下:

/// Interleaved Pair Implementation with less divergence
__global__ void reduceInterleaved(int *g_idata, int *g_odata, unsigned int n)
{
    // set thread ID
    unsigned int tid = threadIdx.x;
    unsigned int idx = blockIdx.x * blockDim.x + threadIdx.x;
    // convert global data pointer to the local pointer of this block
    int *idata = g_idata + blockIdx.x * blockDim.x;
    // boundary check
    if (idx >= n)
        return;
    // in-place reduction in global memory
    for (int stride = blockDim.x / 2; stride > 0; stride >>= 1)
    {
        if (tid < stride)
        {
            idata[tid] += idata[tid + stride];
        }
        __syncthreads();
    }
    // write result for this block to global mem
    if (tid == 0)
        g_odata[blockIdx.x] = idata[0];
}

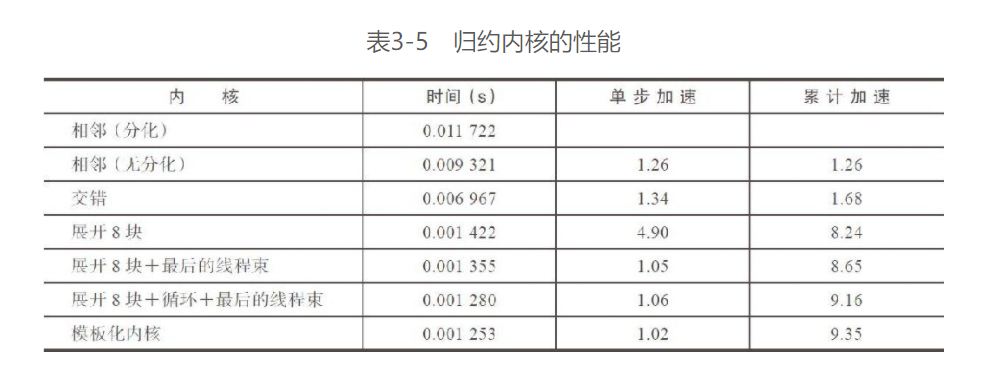
可以看到, 变更为交错配对之后, 交错实现比第一个实现快了1.69倍，比第二个实现快了1.34倍

这种性能的提升主要是由reduceInterleaved函数里的全局内存加载/存储模式导致的

第4章里会介绍更多有关于全局内存加载/存储模式对内核性能的影响

例子:

书里的main函数的基本流程:

获取deviceName并显示
设置指定的device
设置grid & block 执行配置
设置数据量大小
申请主机内存
初始化数据
申请设备内存
cudaMemcpy
主机数据计算
设备warmup
与将要执行的核函数相同, 通过先执行一遍来获得更好的准确性
设备数据计算
设备内存释放
主机内存释放

#include <cuda_runtime.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <random>

#define CHECK(call)                                                             \
    {                                                                           \
        const cudaError_t error = call;                                         \
        if (error != cudaSuccess)                                               \
        {                                                                       \
            printf("Error: %s:%d\n", __FILE__, __LINE__);                       \
            printf("code: %d, reason: %s\n", error, cudaGetErrorString(error)); \
            exit(1);                                                            \
        }                                                                       \
    }


/**
 * @brief reducePlus
 * 改进版的加法交错归约
 * 这里允许使用二维的grid & block
 * @param g_idata   全局数据输入
 * @param g_odata   全局数据输出
 * @param size      数据量
 * @return void
 */
__global__ void reducePlus(int *g_idata, int *g_odata, unsigned int size)
{
    //线程块内号
    unsigned int tid = threadIdx.x + threadIdx.y * blockDim.x;
    unsigned int bid = blockIdx.x + blockIdx.y * gridDim.x;
    unsigned int blockThreadNum = blockDim.x * blockDim.y;
    //线程号对应的g_idata的index
    unsigned int idx = bid*blockThreadNum+tid;
    if(idx>=size){
        return ;
    }
    //当前块需要处理的第一个数据的地址
    int *idata = g_idata + blockThreadNum * (bid) ;
    //i为步长
    for (int i = blockThreadNum / 2; i > 0; i >>= 1)
    {
        if (tid < i)
        {
            idata[tid] += idata[tid + i];
        }
        __syncthreads();
    }
    if (!tid)
    {
        g_odata[bid] = idata[0];
    }
    return;
}

/**
 * @brief 
 * 生成[0,1]的浮点随机数
 * @return int
 */
int myRand()
{
    return rand() & 0x0f;
}

/**
 * @brief 
 * CPU 交错归约 
 * @param data 
 * @param size 
 * @return int 
 */
int recursiveReduce(int *data, const int size)
{
    if (size == 1)
    {
        return data[0];
    }
    const int stride = size / 2;
    for (int i = 0; i < stride; ++i)
    {
        data[i] += data[i + stride];
    }
    return recursiveReduce(data, stride);
}

int main(int argc, char **argv)
{
    // 检测并初始化设备
    int dev = 0;
    cudaDeviceProp deviceProp;
    cudaGetDeviceProperties(&deviceProp, dev);
    // printf("%s starting at ", argv[0]);
    printf("starting at device %d: %s \n", dev, deviceProp.name);
    cudaSetDevice(dev);
    bool bResult = false;

    // 初始化数据
    int size = 1 << 26; // total number of elements to reduce
    printf("Array size : %d ", size);

    //执行配置
    //将线程数开到6400
    dim3 block(1 << 7, 1 << 3, 1);
    dim3 grid(1 << 10, 1 << 6, 1);
    const int blockNum = grid.x * grid.y * grid.z;
    printf("executing config : <<<(%d, %d, %d) (%d, %d, %d)>>>\n",
           grid.x, grid.y, grid.z, block.x, block.y, block.z);

    // 申请主机内存
    size_t bytes = size * sizeof(int);
    int *h_idata = (int *)malloc(bytes);
    int *h_odata = (int *)malloc(blockNum * sizeof(int));
    int *tmp = (int *)malloc(bytes);
    // 初始化数据
    srand(time(0));
    for (int i = 0; i < size; i++)
    {
        // 使用[0,1]的浮点
        h_idata[i] = myRand();
    }
    for(int i=0;i<10;++i){
        printf("%d ", h_idata[i]);
    }
    putchar('\n');
    memcpy(tmp, h_idata, bytes);
    size_t iStart, iElaps;
    int gpu_sum = 0;
    // 申请设备内存
    int *d_idata = NULL;
    int *d_odata = NULL;
    CHECK(cudaMalloc((void **)&d_idata, bytes));
    CHECK(cudaMalloc((void **)&d_odata, blockNum * sizeof(int)));

    // cpu reduction
    iStart = clock();
    int cpu_sum = recursiveReduce(tmp, size);
    iElaps = clock() - iStart;
    printf("cpu 归约计算完成, 耗时 %d ms cpu_sum: %d\n", iElaps, cpu_sum);

    // 设备warmup
    CHECK(cudaMemcpy(d_idata, h_idata, bytes, cudaMemcpyHostToDevice));
    cudaDeviceSynchronize();
    iStart = clock();
    // auto warmup=reducePlus;
    reducePlus<<<grid, block>>>(d_idata, d_odata, size);
    cudaDeviceSynchronize();
    iElaps = clock() - iStart;
    CHECK(cudaMemcpy(h_odata, d_odata, blockNum * sizeof(int), cudaMemcpyDeviceToHost));
    gpu_sum = 0;
    for (int i = 0; i < blockNum; i++)
        gpu_sum += h_odata[i];
    printf("gpu Warmup 完成, 耗时 %d ms gpu_sum: %d \n",
           iElaps, gpu_sum);

    // 设备归约
    CHECK(cudaMemcpy(d_idata, h_idata, bytes, cudaMemcpyHostToDevice));
    cudaDeviceSynchronize();
    iStart = clock();
    reducePlus<<<grid, block>>>(d_idata, d_odata, size);
    cudaDeviceSynchronize();
    iElaps = clock() - iStart;
    CHECK(cudaMemcpy(h_odata, d_odata, blockNum * sizeof(int), cudaMemcpyDeviceToHost));
    gpu_sum = 0;
    for (int i = 0; i < blockNum; i++)
        gpu_sum += h_odata[i];
    printf("gpu 归约完成, 耗时 %d ms gpu_sum: %d \n",
           iElaps, gpu_sum);
    cudaDeviceSynchronize();

    /// free host memory
    free(h_idata);
    free(h_odata);
    // free device memory
    cudaFree(d_idata);
    cudaFree(d_odata);
    // reset device
    cudaDeviceReset();
    // check the results
    bResult = (gpu_sum == cpu_sum);
    if (!bResult)
        printf("Test failed!\n");
    return EXIT_SUCCESS;
}

输出结果:

starting at device 0: GeForce GTX 1050
Array size : 67108864 executing config : <<<(1024, 64, 1) (128, 8, 1)>>>
12 7 7 0 5 5 7 13 9 10
cpu 归约计算完成, 耗时 145 ms cpu_sum: 503316480
gpu Warmup 完成, 耗时 28 ms gpu_sum: 503316480
gpu 归约完成, 耗时 23 ms gpu_sum: 503316480

这里的随机数之和多次启动的结果就是不变

分析:

这个例子中还有很多可改进的地方:

所开的线程数必须与数据量相同
由于每次仅启动一半的线程进行计算, 一个线程计算两个数, 所以需要线程数=数据量
每个线程仅进行一次加法计算:
这个是后头循环展开的部分, 通过提升每个线程每次循环的计算量, 线程数将更快收敛, 并且得到更好的效能
线程数与数据量强耦合
可以实现线程数与数据量的解耦合, 但实现起来较为复杂:
- 数据量>线程数时:
  必须启动所有线程进行计算
- 数据量<=线程数时:
  折半启动线程进行计算
  
  这里如果要实现循环展开的话也需要手动调整每次循环的计算量

3.5 循环展开:

总觉得书里翻译的有问题, 说的还非常拗口

循环展开是一种经典的优化循环的方法, 通过增加每次迭代中计算元素的数量来减少循环的迭代次数

其实就是……在一次循环中完成多次循环的任务

在CPU中, 循环展开能带来直接的性能提升:

操作	整数	整数(优化后)	浮点数	浮点数(优化后)
+	360	163	354	164
-	379	167	341	177
*	350	160	364	163
/	118	57	152	63

这是由于减少了循环判断的次数以及其他的原因

在CUDA中, 循环展开的目标是:
通过减少指令消耗和增加更多的独立调度指令来提高性能, 由此, 更多的并发操作可以被添加到流水线上, 以产生更高的指令和内存带宽, 帮助隐藏指令&内存延时

展开的归约

本部分在上一小节的内容上进行修改

上一节中的交错归约核函数中, 每个block仅处理一份源数据, 现在扩充到原先的两倍进行测试:

__global__ void reduceUnrolling2 (int *g_idata, int *g_odata, unsigned int n) {
    // set thread ID
    //线程块内号
    unsigned int tid = threadIdx.x;
    //线程号对应的g_idata的index
    unsigned int idx = blockIdx.x * blockDim.x * 2 + threadIdx.x;
 
    // convert global data pointer to the local pointer of this block
    //当前块需要处理的第一个数据的地址
    int *idata = g_idata + blockIdx.x * blockDim.x * 2;
 
    // unrolling 2 data blocks
    //如果当前idx位置能够处理两份的数据(没有超限), 则处理两份的数据(将第二份数据加到第一份数据上)
    if (idx + blockDim.x < n) g_idata[idx] += g_idata[idx + blockDim.x];
    __syncthreads();
 
    // in-place reduction in global memory
    //这部分与原版本相同
    for (int stride = blockDim.x / 2; stride > 0; stride >>= 1) {
        if (tid < stride) {
            idata[tid] += idata[tid + stride];
        }
        // synchronize within threadblock
        __syncthreads();
    }
 
    // write result for this block to global mem
    if (tid == 0) g_odata[blockIdx.x] = idata[0];
}

对主机代码进行简单的修改
由于每个线程处理两倍与原来的数据, 所以将grid大小/2

结果:

相较于原来快了3.42倍
并且进一步展开归约之后, 能够获得更好的性能

这是由于在一个线程中, 更多的独立内存LD/ST (加载/存储)操作能更好的将内存延时隐藏起来

查看内存吞吐量指标也能看见, 显存吞吐量是不断上升的

全局读取效率:

展开线程的归约

本部分针对上头的例子中, 启动的线程数<=32的情况

CUDA线程束的执行是SIMT的, 每条指令之后都有一个隐式的线程束内同步过程

为了进一步循环展开, 在线程数<=32时退出循环, 直接手写剩下的归并操作, 同时将线程每循环操作数调到8

最终结果:

查看线程束阻塞:

nvprof.exe --metrics stall_sync .\cuda_main.exe

对比处理一份数据与处理8份数据:

可以看到线程束的阻塞下降的很明显

完全展开的归约

这里就是将循环完全的展开

因为在一定的GPU架构中, 每个块的最大线程数都是固定的, Fermi & Kepler =1024 , Pascal = 2048
所以将循环完全展开是可能的:

结果是内核执行时间再一次的缩短:

模板函数的归约

这里就是使用CUDA支持的模板函数去实现上述循环完全展开的过程

上一个例子中, 其中有很多if判断, 一定程度上影响了程序的效率
可以使用模板函数去替换

CUDA的模板其实就是C++的语法, 这里的语法看起来有点奇怪………

调用部分:

使用template的好处是在编译期间就能进行评估, 如果if为false, 则编译时将直接删除该语句, 提升循环效率

结果:

3.6 动态并行:

本部分就是使用GPU启动核函数

之前用的都是CPU创建核函数, 而动态并行功能允许GPU启动核函数, 以实现递归功能
并可以推迟运行时决定在GPU上创建的grid & block的数量, 利用GPU硬件调度器 & 加载平衡器动态的调整以适应数据驱动或工作的负载, 并能一定程度上减少主机与设备之间的传输(控制&数据流)需求

注意, 动态并行只有在计算能力为3.5或更高的设备上才能被支持, 老版本的卡(低于Kepler架构)是无法使用动态并行的

嵌套执行

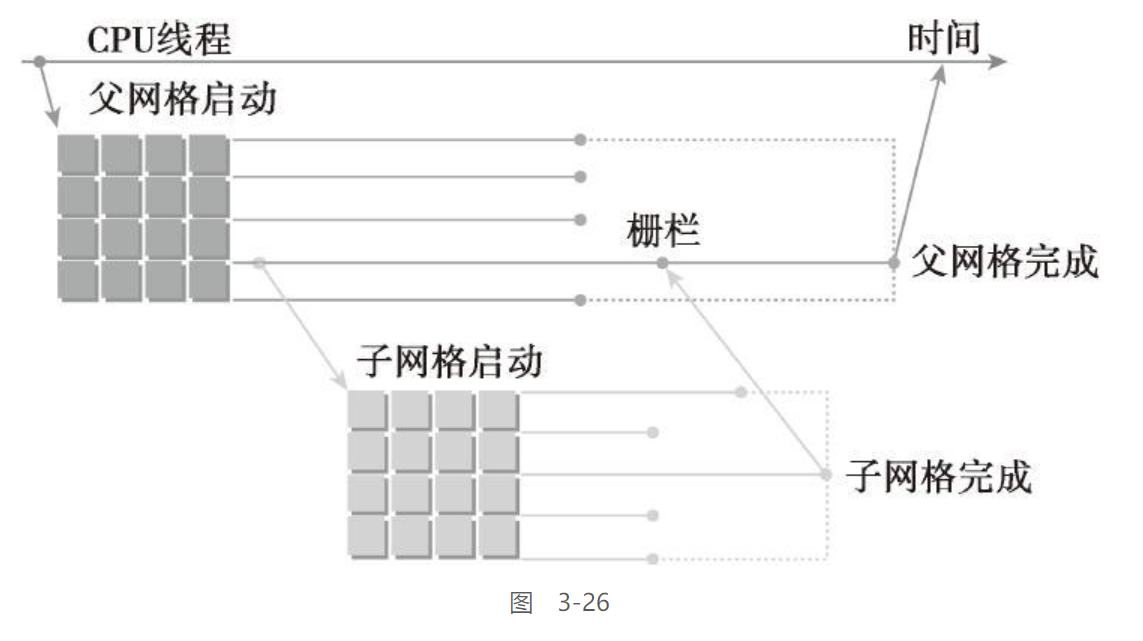
在动态并行中，内核执行分为两种类型：父母和孩子。父线程、父线程块或父网格启动一个新的网格，即子网格。子线程、子线程块或子网格被父母启动。子网格必须在父线程、父线程块或父网格完成之前完成。只有在所有的子网格都完成之后，父母才会完成

如果调用的线程没有显式的进行同步启动子网络, 那么运行时将保证父母和孩子之间的隐式同步

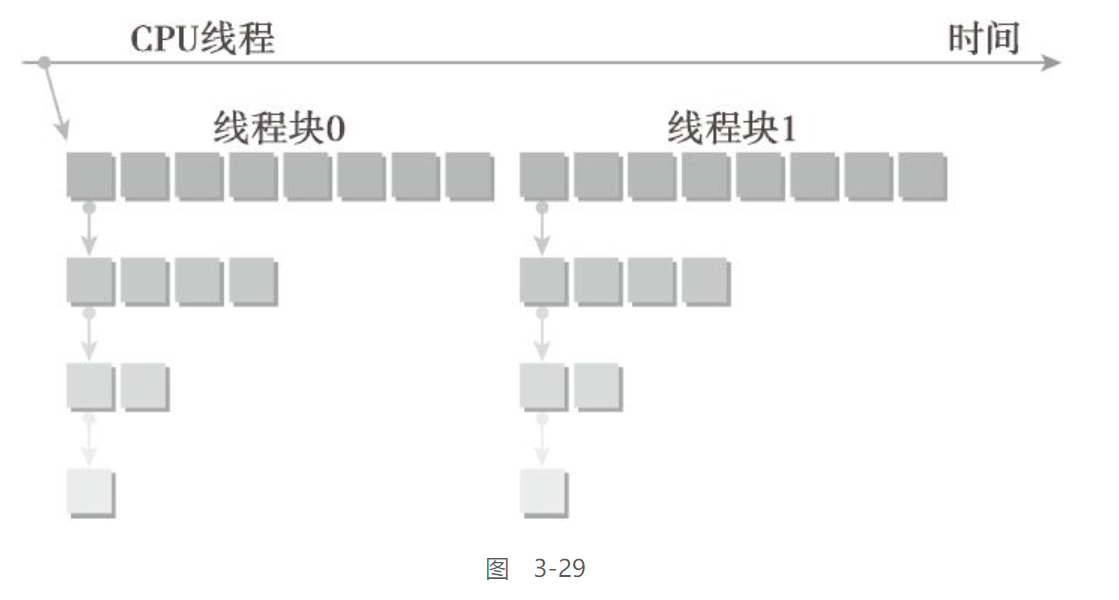
如下图所示:

嵌套执行的几个特点:

设备线程中的网格启动，在线程块间是可见的

这句话我感觉翻译的有问题, 是线程块内还是线程块间? 后头的解释明显是线程块内, 但是他这里翻译为线程块间

这意味着, 该线程可能和同一个线程块中任意线程启动的子grid同步

所以, 在一个线程块中, 仅有当所有线程创建的所有子网格完成之后, 线程块才能完成执行, 也就是说, 块中的所有线程在退出时, 会触发一个与所有子网格的隐式同步
当父母启动一个子网格，父线程块与孩子显式同步之后，孩子才能开始执行
父网格和子网格共享相同的全局内存和常量内存，但它们有不同的局部内存和共享内存
有了孩子和父母之间的弱一致性作为保证，父网格和子网格可以对全局内存并发存取

这里的内存操作很绕(翻译可真是个崽种), 简单看下即可, 后头的例子会详细说明

有两个时刻，子网格和它的父线程见到的内存完全相同：子网格开始时和子网格完成时。当父线程优于子网格调用时，所有的全局内存操作要保证对子网格是可见的。当父母在子网格完成时进行同步操作后，子网格所有的内存操作应保证对父母是可见的。

共享内存和局部内存分别对于线程块或线程来说是私有的，同时，在父母和孩子之间不是可见或一致的。局部内存对线程来说是私有存储，并且对该线程外部不可见。当启动一个子网格时，向局部内存传递一个指针作为参数是无效的。

在GPU上嵌套Hello World

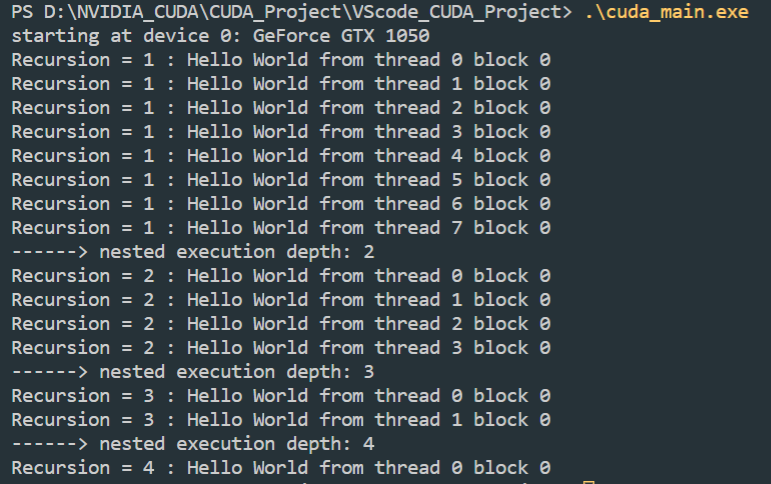
总之先来一个Hello World:

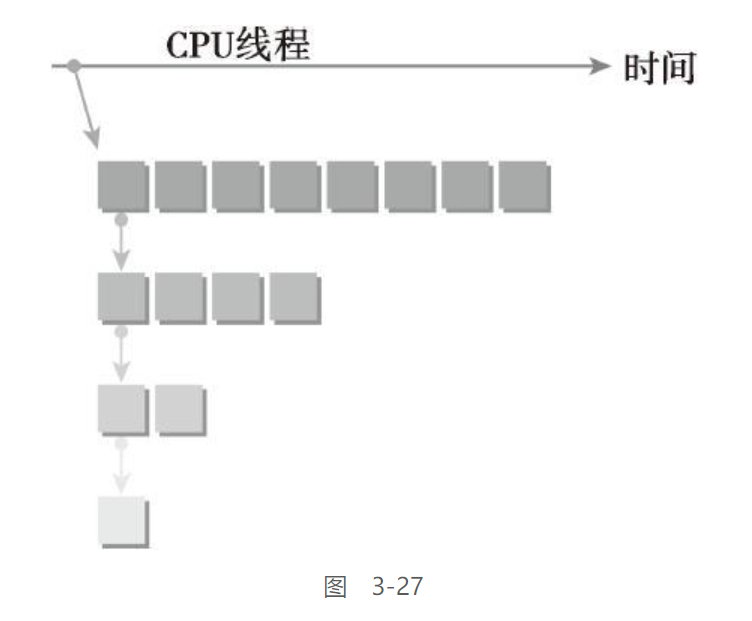
基本的调用思路如下:

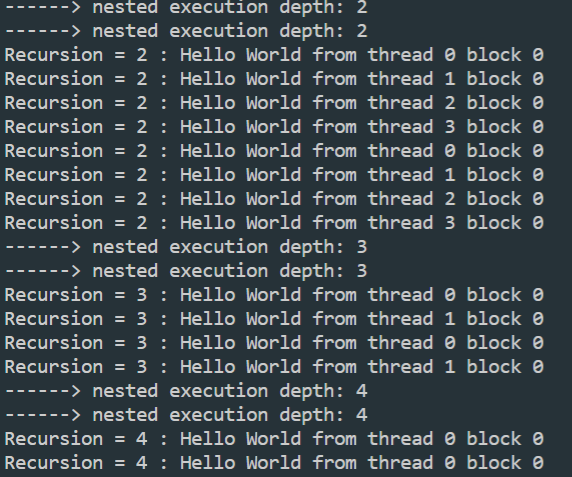
主机应用程序调用父网格，该父网格在一个线程块中有8个线程。然后，该父网格中的线程0调用一个子网格，该子网格中有一半线程，即4个线程。之后，第一个子网格中的线程0再调用一个新的子网格，这个新的子网格中也只有一半线程，即2个线程，以此类推，直到最后的嵌套中只剩下一个线程。

/**
 * @brief 
 * 递归输出hello world
 * @param iSize     线程块大小
 * @param iDepth    递归深度
 * @return __global__ 
 */
__global__ void nestedHelloWorld(const int iSize, int iDepth){
    int tid=threadIdx.x;
    printf("Recursion = %d : Hello World from thread %d block %d \n", iDepth, tid, blockIdx.x);
    if(iSize==1){
        return ;
    }
    int nthreads=iSize>>1;

    if(tid==0 && nthreads>0){
        nestedHelloWorld<<<1, nthreads>>> (nthreads, ++iDepth);
        printf("------> nested execution depth: %d\n", iDepth);
    }
    
    return; 
}

完整程序:

#include <cuda_runtime.h>
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
#include <random>

#define CHECK(call)                                                             \
    {                                                                           \
        const cudaError_t error = call;                                         \
        if (error != cudaSuccess)                                               \
        {                                                                       \
            printf("Error: %s:%d\n", __FILE__, __LINE__);                       \
            printf("code: %d, reason: %s\n", error, cudaGetErrorString(error)); \
            exit(1);                                                            \
        }                                                                       \
    }

/**
 * @brief 
 * 递归输出hello world
 * @param iSize     线程块大小
 * @param iDepth    递归深度
 * @return __global__ 
 */
__global__ void nestedHelloWorld(const int iSize, int iDepth){
    int tid=threadIdx.x;
    printf("Recursion = %d : Hello World from thread %d block %d \n", iDepth, tid, blockIdx.x);
    if(iSize==1){
        return ;
    }
    int nthreads=iSize>>1;

    if(tid==0 && nthreads>0){
        nestedHelloWorld<<<1, nthreads>>> (nthreads, ++iDepth);
        printf("------> nested execution depth: %d\n", iDepth);
    }
    
    return; 
}


int main(int argc, char **argv)
{
    // 检测并初始化设备
    int dev = 0;
    cudaDeviceProp deviceProp;
    cudaGetDeviceProperties(&deviceProp, dev);
    // printf("%s starting at ", argv[0]);
    printf("starting at device %d: %s \n", dev, deviceProp.name);
    cudaSetDevice(dev);

    nestedHelloWorld<<<1,8>>>(8, 1);

    cudaDeviceReset();

    return EXIT_SUCCESS;
}

注意这里的编译要加上额外的参数, 否则编译失败

nvcc -arch=sm_61 -rdc=true .\cuda_main.cu -o cuda_main.exe -lcudadevrt

-rdc=true

当-rdc=true时, 强制nvcc生成可重定位的设备代码, 在使用动态并行时的一个硬性要求
-lcudadevrt

因为动态并行是由设备运行时库所支持的, 所以必须使用-lcudadevrt

输出:

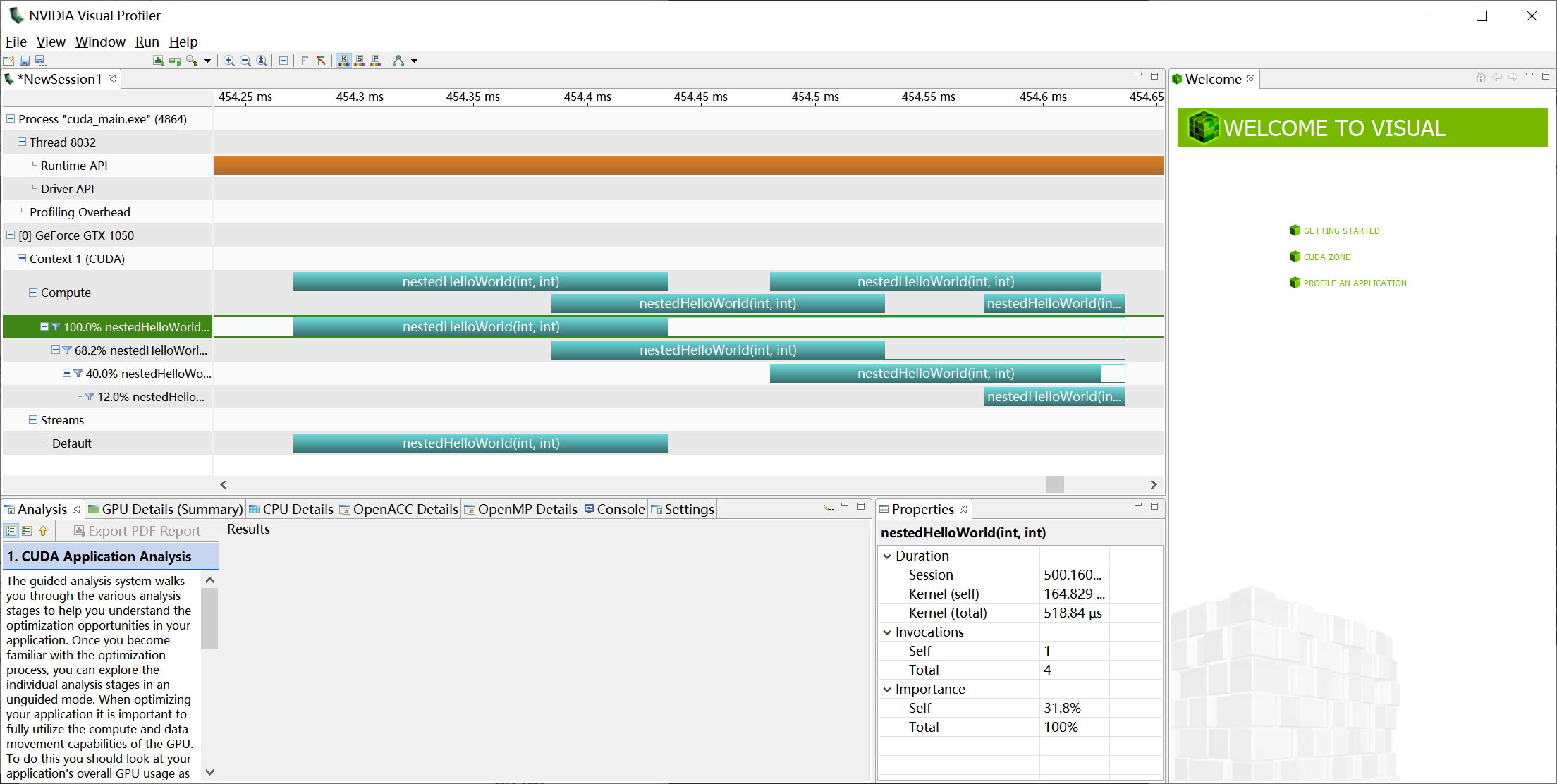
使用nvvp查看的结果:

可以看到父线程确实是在子线程return之后在结束的

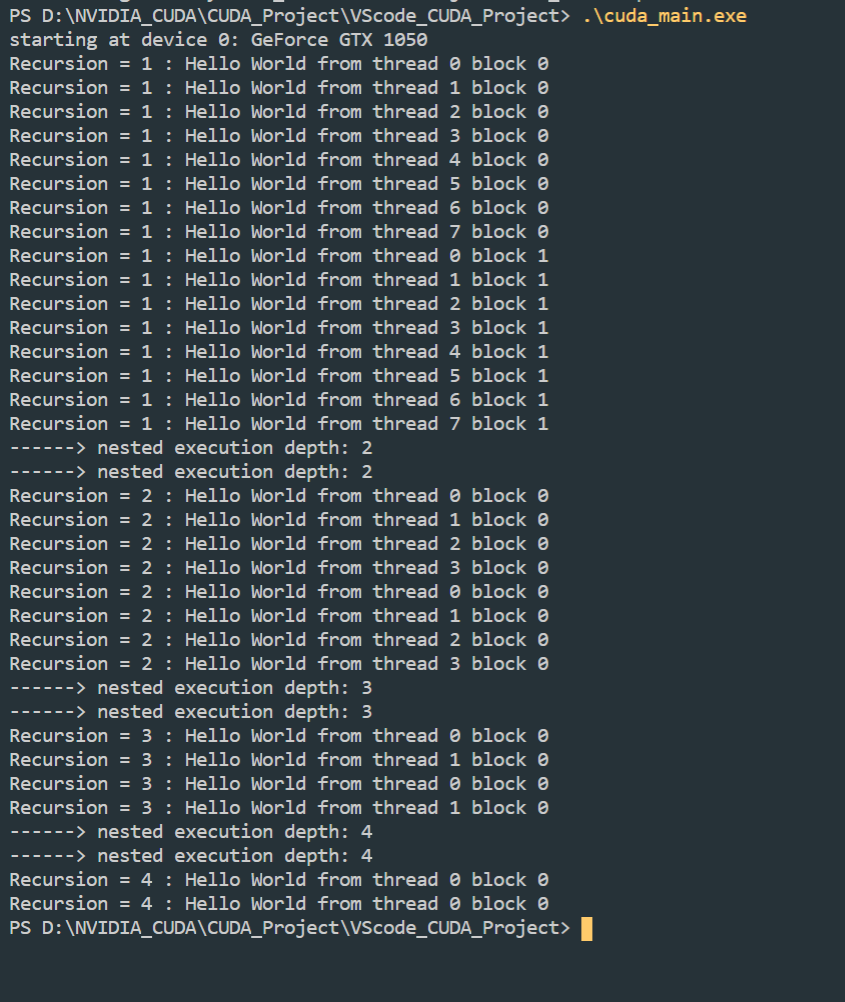
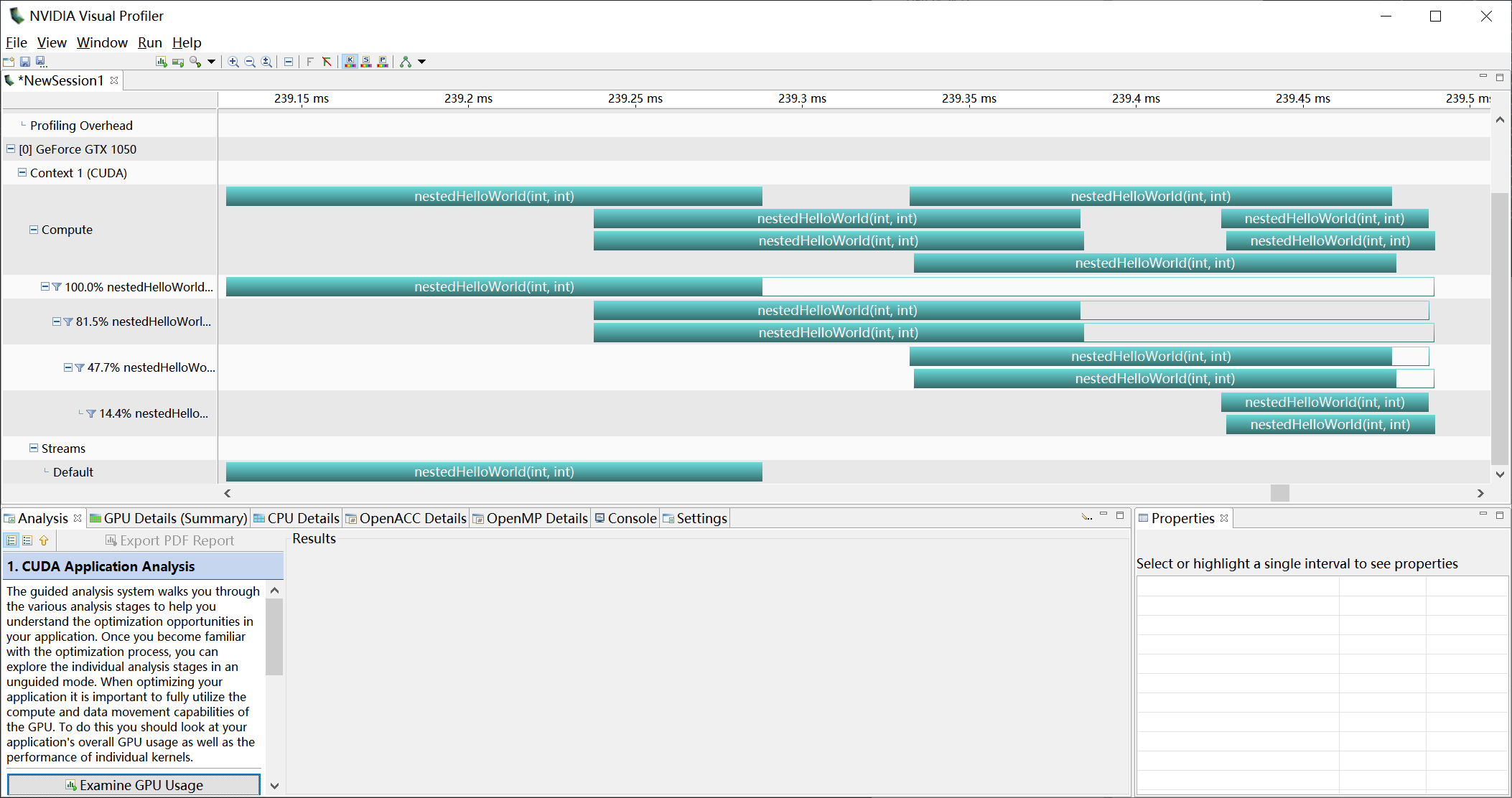
使用2个grid调用的结果:

这里可以发现一个奇怪之处, 子线程块的blockIdx.x都=0, 这是由于仅在最上层的父线程中使用了两个线程块, 而其余的子线程均只有一个线程块

动态并行的物理限制:

动态并行的最大嵌套深度限制为24，但是实际上，在每一个新的级别中大多数内核受限于设备运行时系统需要的内存数量。因为为了对每个嵌套层中的父网格和子网格之间进行同步管理，设备运行时要保留额外的内存。

嵌套归约

这里就是使用递归的核函数方法实现之前的循环版本归约

这里就基本可以实现和归并排序类似的递归方案了

但是需要注意的是, 众所周知递归是比循环更加消耗资源的一种算法实现
所以如果可以的话, 最好还是采用循环展开

代码实现如下:

__global__ void gpuRecursiveReduce(int *g_idata, int *g_odata,
                                   unsigned int isize)
{
    // set thread ID
    unsigned int tid = threadIdx.x;
    // convert global data pointer to the local pointer of this block
    int *idata = g_idata + blockIdx.x * blockDim.x;
    int *odata = &g_odata[blockIdx.x];
    // stop condition
    if (isize == 2 && tid == 0)
    {
        g_odata[blockIdx.x] = idata[0] + idata[1];
        return;
    }
    // nested invocation
    int istride = isize >> 1;
    if (istride > 1 && tid < istride)
    {
        // in place reduction
        idata[tid] += idata[tid + istride];
    }
    // sync at block level
    __syncthreads();
    // nested invocation to generate child grids
    if (tid == 0)
    {
        gpuRecursiveReduce<<<1, istride>>>(idata, odata, istride);
        // sync all child grids launched in this block
        cudaDeviceSynchronize();
    }
    // sync at block level again
    __syncthreads();
}

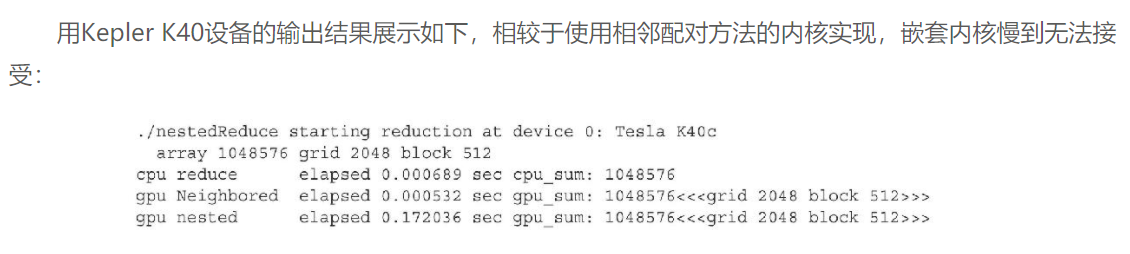
但是内核的执行效率很糟糕:

主要是由于调用了过多的线程块同步__syncthreads(), 导致了性能低下

当一个子网格被调用后，它看到的内存与父线程是完全一样的。因为每一个子线程只需要父线程的数值来指导部分归约，所以在每个子网格启动前执行线程块内部的同步是没有必要的

减少__syncthreads数量之后的函数如下:

__global__ void gpuRecursiveReduceNosync(int *g_idata, int *g_odata, unsigned int isize)
{
    // set thread ID
    unsigned int tid = threadIdx.x;
    // convert global data pointer to the local pointer of this block
    int *idata = g_idata + blockIdx.x * blockDim.x;
    int *odata = &g_odata[blockIdx.x];
    // stop condition
    if (isize == 2 && tid == 0)
    {
        g_odata[blockIdx.x] = idata[0] + idata[1];
        return;
    }
    // nested invoke
    int istride = isize >> 1;
    if (istride > 1 && tid < istride)
    {
        idata[tid] += idata[tid + istride];
        if (tid == 0)
        {
            gpuRecursiveReduceNosync<<<1, istride>>>(idata, odata, istride);
        }
    }
}

运行之后的耗时缩短为原先的1/3, 但相较于之前循环版本的归约, 性能仍然很差

主要原因是这两种方法都创建了过多的子网络(16384个grid)

换一种思路来实现这个过程:

网格中第一个线程块中的第一个线程在每一步嵌套时都调用子网格。比较这两个核函数的特征码，会发现多了一个参数。因为每次嵌套调用时，子线程块大小会减到其父线程块大小的一半，父线程块的维度也必须传递给嵌套的子网格。这使得每个线程都能为它的工作负载部分正确计算出消耗部分的全局内存偏移地址。值得注意的是，在这个实现中，所有空闲的线程都是在每次内核启动时被移除的，而对于第一次实现而言，在每个嵌套层的内核执行过程中都会有一半的线程空闲下来。这样的改变将会释放一半的被第一个核函数消耗的计算资源，这样可以让更多的线程块活跃起来。

__global__ void gpuRecursiveReduce2(int *g_idata, int *g_odata, int iStride, int const iDim)
{
    // convert global data pointer to the local pointer of this block
    int *idata = g_idata + blockIdx.x * iDim;
    // stop condition
    if (iStride == 1 && threadIdx.x == 0)
    {
        g_odata[blockIdx.x] = idata[0] + idata[1];
        return;
    }
    // in place reduction
    idata[threadIdx.x] += idata[threadIdx.x + iStride];
    // nested invocation to generate child grids
    if (threadIdx.x == 0 && blockIdx.x == 0)
    {
        gpuRecursiveReduce2<<<gridDim.x, iStride / 2>>>(
            g_idata, g_odata, iStride / 2, iDim);
    }
}

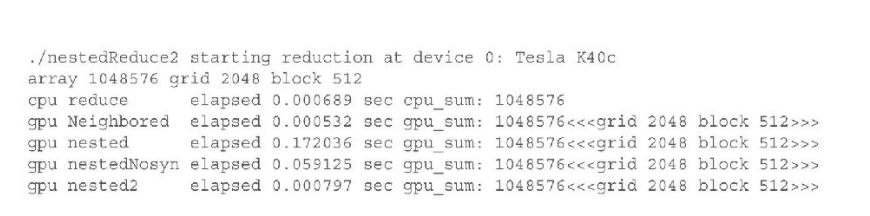
由此的性能就可以非常接近于之前的循环模式了:

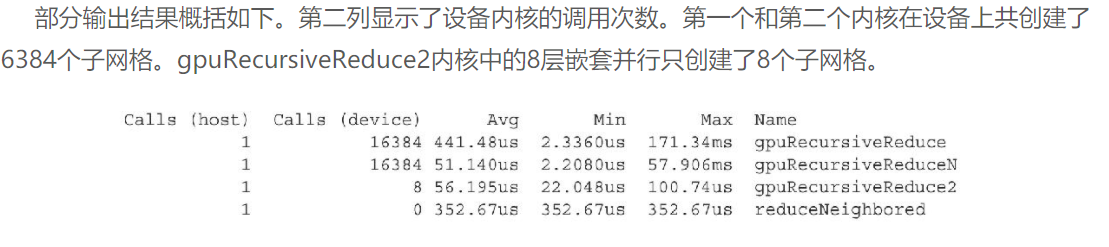
使用nvprof来查看核函数的调用:

明显的观察到设备递归调用的减少

所以以上例子说明了:

在使用嵌套执行时避免大量嵌套, 能显著的提升性能
避免使用过多的线程块同步__syncthreads

3.7 总结:

本章从硬件的角度分析了内核执行。在GPU设备上，CUDA执行模型有两个最显著的特性：

使用SIMT方式在线程束中执行线程
在线程块与线程中分配了硬件资源

这些执行模型的特征使得我们在提高并行性和性能时，能控制应用程序是如何让指令和内存带宽饱和的。不同计算能力的GPU设备有不同的硬件限制，因此，网格和线程块的启发式算法在为不同平台优化内核性能方面发挥了非常重要的作用。

动态并行使设备能够直接创建新的工作。它确保我们可以用一种更自然和更易于理解的方式来表达递归或依赖数据并行的算法。为实现一个有效的嵌套内核，必须注意设备运行时的使用，其包括子网格启动策略、父子同步和嵌套层的深度。

本章也介绍了使用命令行分析工具nvprof详细分析内核性能的方法。因为一个单纯的内核实现可能不会产生很好的性能，所以配置文件驱动的方法在CUDA编程中尤其重要。性能分析对内核行为提供了详细的分析，并能找到产生最佳性能的主要因素。

在第4章和第5章，将会从CUDA内存模型的角度介绍内核执行的内容。