Density-based Clustering
第二种类型的聚类算法叫做“密度聚类”,即基于密度的聚类。这一类模型是根据样本之间的紧密程度进行聚类,通过样本的密度来考虑样本之间的可连接性。其中,DBSCAN是最为著名的密度聚类模型。DBSCAN基于一组“邻域”参数 ( ϵ , M i n P t s ) (\epsilon, \ MinPts) (ϵ, MinPts)来刻画样本之间的紧密程度,给定数据集 D = { x 1 , x 2 , … , x n } D=\{x_1,x_2,\dots,x_n\} D={x1,x2,…,xn},有以下几个重要概念:
- ϵ \epsilon ϵ-邻域:对于 x j ∈ D x_j\in D xj∈D,其 ϵ \epsilon ϵ-邻域是数据集 D D D中所有与 x j x_j xj距离不大于 ϵ \epsilon ϵ的样本,即 N ϵ ( x j ) = { x i ∈ D ∣ d i s t ( x i , x j ) ≤ ϵ } N_{\epsilon}(x_j)=\{x_i \in D\ |\ dist(x_i, x_j)\le \epsilon \} Nϵ(xj)={xi∈D ∣ dist(xi,xj)≤ϵ}
- 核心对象(core object):若 x j x_j xj的 ϵ \epsilon ϵ邻域中至少包含 M i n P t s MinPts MinPts个样本,即 ∣ N ϵ ( x j ) ∣ ≥ M i n P t s |N_{\epsilon}(x_j)|\ge MinPts ∣Nϵ(xj)∣≥MinPts,那么 x j x_j xj就被叫做一个核心对象
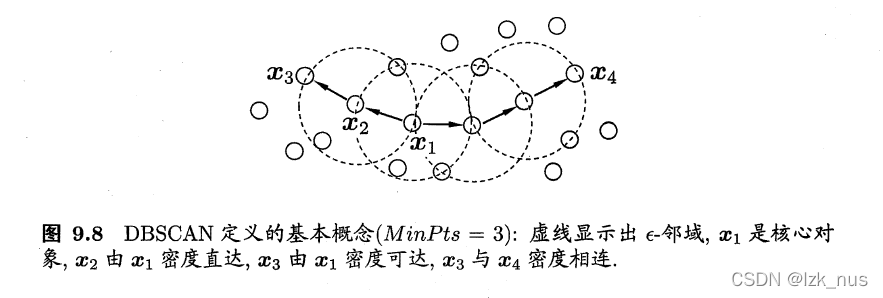
- 密度直达(directly density-reachable):若 x j x_j xj在 x i x_i xi的邻域里,且 x i x_i xi是核心对象,那么称 x i x_i xi和 x j x_j xj是密度直达的
- 密度可达(density reachable):对 x i x_i xi和 x j x_j xj,若存在样本序列 p 1 , p 2 , … , p n p_1, p_2, \dots, p_n p1,p2,…,pn,其中 p 1 = x i , p n = x j p_1=x_i, \ p_n=x_j p1=xi, pn=xj,且 p i + 1 p_{i+1} pi+1可由 p i p_i pi密度直达,那么称 x i x_i xi和 x j x_j xj密度可达
- 密度相连(density connected):对 x i x_i xi和 x j x_j xj,若存在 x k x_k xk使得 x i x_i xi和 x j x_j xj均和 x k x_k xk密度可达,那么称 x i x_i xi和 x j x_j xj密度相连
基于以上概念,DBSCAN对“簇”的定义为:由密度可达关系导出的最大的密度相连样本集合。给定参数 ( ϵ , M i n P t s ) (\epsilon,MinPts) (ϵ,MinPts),簇 C ⊆ D C\subseteq D C⊆D,那么 C C C满足以下性质:
- 连接性: x i , x j ∈ C ⇒ x i x j x_i, \ x_j\ \in\ C\ \ \ \ \ \Rightarrow\ \ \ \ x_i\ x_j xi, xj ∈ C ⇒ xi xj密度相连
- 最大性: x i ∈ C x_i \in C xi∈C, x i x_i xi和 x j x_j xj密度可达 ⇒ x j ∈ C \ \ \ \ \ \Rightarrow\ \ \ \ x_j\in C ⇒ xj∈C
在实际写代码过程中,假如 x x x是一个核心对象,那么只需要找到所有和 x x x密度可达的样本 x ^ \hat{x} x^,那么这些样本所组成的是一个簇。算法流程如下: