代码随想录训练营 Day14打卡 二叉树 part02

一、 力扣226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
示例 ：

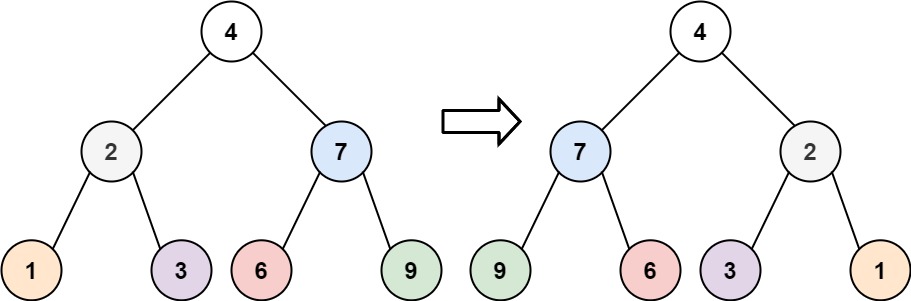
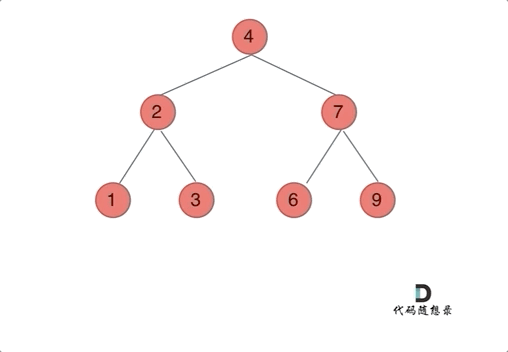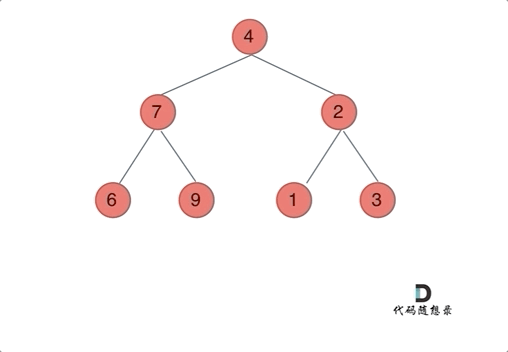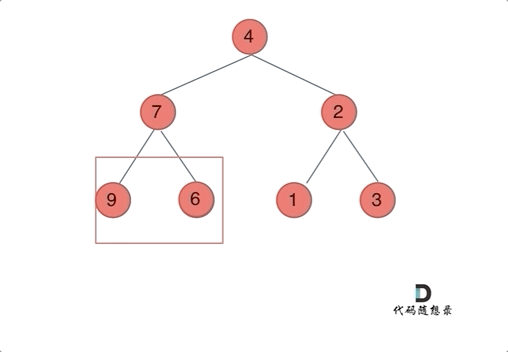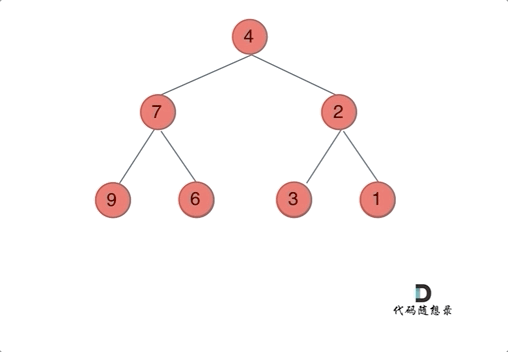
输入： root = [4,2,7,1,3,6,9]
输出： [4,7,2,9,6,3,1]

我们下文以前序遍历为例，通过动画来看一下翻转的过程:

版本一 递归法 前序遍历

思路：前序遍历的递归方法首先交换当前节点的左右子节点，然后递归地翻转左右子树。这是最直接的方法，因为它先处理当前节点，再递归处理子节点。

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        # 交换当前节点的左右子树
        root.left, root.right = root.right, root.left
        # 递归翻转左子树
        self.invertTree(root.left)
        # 递归翻转右子树
        self.invertTree(root.right)
        return root

版本二 迭代法 前序遍历

思路：迭代使用栈来模拟递归的前序遍历。首先将根节点放入栈中，然后在每次从栈中取出一个节点时，交换它的左右子节点，并将子节点按右左顺序推入栈中。

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None      
        stack = [root]        
        while stack:
            node = stack.pop()
            node.left, node.right = node.right, node.left
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)  
        return root

版本三 递归法 中序遍历

思路：中序遍历的递归方法与前序类似，但它在翻转左子树后交换左右子树，然后再递归翻转新的左子树（原右子树）。

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None
        # 先递归处理左子树
        self.invertTree(root.left)
        # 交换左右子树
        root.left, root.right = root.right, root.left
        # 注意这里需要再次递归处理新的左子树（原来的右子树）
        self.invertTree(root.left)
        return root

版本四 迭代法 中序遍历

思路：后序遍历的递归方法先处理所有子节点，然后再处理当前节点，即先翻转所有子树，然后交换左右子树。

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None      
        stack = []
        current = root
        while stack or current:
            while current:
                stack.append(current)
                current = current.left
            current = stack.pop()
            # 交换操作
            current.left, current.right = current.right, current.left
            # 处理右子树
            current = current.left
        return root

版本五 迭代法 后序遍历

思路：迭代的后序遍历使用栈来先处理所有子节点，然后在从栈中取出节点时进行交换。

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        if not root:
            return None      
        stack = [root]        
        while stack:
            node = stack.pop()                   
            if node.left:
                stack.append(node.left)
            if node.right:
                stack.append(node.right)  
            node.left, node.right = node.right, node.left               
     
        return root

版本六 迭代法 广度优先遍历（层序遍历）

思路：层序遍历使用队列来逐层交换节点的左右子节点。每次从队列中取出一个节点时交换其子节点，然后将子节点加入队列中。

class Solution:
    def invertTree(self, root: TreeNode) -> TreeNode:
        # 如果根节点为空，则直接返回None
        if not root: 
            return None

        # 使用队列来进行层序遍历，初始时队列中只有根节点
        queue = collections.deque([root])    
        while queue:
            # 处理当前层的所有节点
            for i in range(len(queue)):
                # 从队列中弹出当前节点
                node = queue.popleft()
                # 交换当前节点的左右子节点
                node.left, node.right = node.right, node.left
                # 如果左子节点存在，将其加入队列
                if node.left: 
                    queue.append(node.left)
                # 如果右子节点存在，将其加入队列
                if node.right: 
                    queue.append(node.right)
        return root   

力扣题目链接
题目文章讲解
题目视频讲解

二、 力扣101. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。
示例 ：

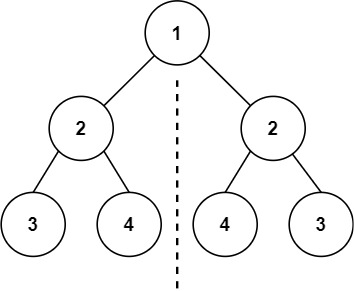
输入： root = [1,2,2,3,4,4,3]
输出： true

对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

那么如何比较呢？

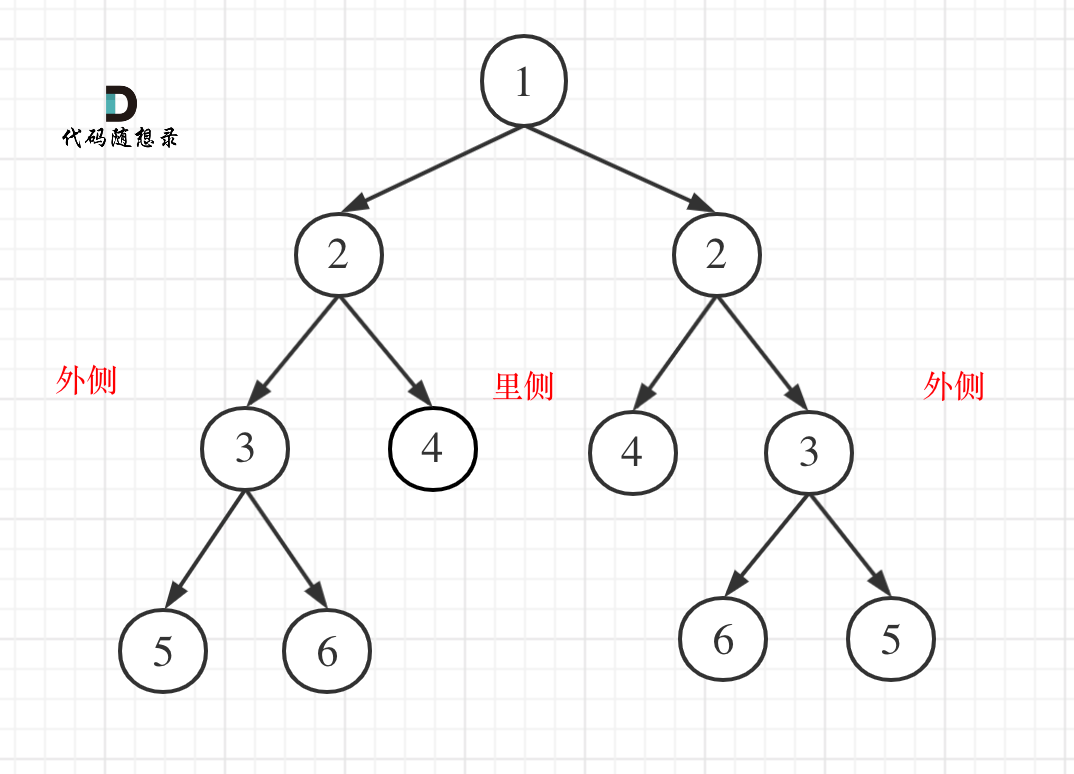
比较的是两个子树的里侧和外侧的元素是否相等。如图所示：

那么遍历的顺序应该是什么样的呢？

本题遍历只能是“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。

正是因为要遍历两棵树而且要比较内侧和外侧节点，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

但都可以理解算是后序遍历，尽管已经不是严格上在一个树上进行遍历的后序遍历了。

实现思路：

1. 定义递归函数： 递归函数接收两个节点作为参数，分别为来自两棵子树的对应节点。
2. 递归终止条件： 如果两个节点都为空，返回 True；如果一个为空另一个不为空，或者两个节点的值不相同，返回 False。
3. 递归比较逻辑： 递归比较一个节点的左子节点与另一个节点的右子节点，以及一个节点的右子节点与另一个节点的左子节点。

版本一 递归法

实现思路：这种方法通过递归判断每一层的对称性，确保树的每一层都是对称的。首先排除空节点的情况，然后再递归比较外侧和内侧节点。

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True  # 如果根节点为空，树是对称的
        return self.compare(root.left, root.right)  # 从根节点的两个子节点开始比较
    
    def compare(self, left, right):
        # 处理节点为空的情况
        if left == None and right != None:
            return False
        elif left != None and right == None:
            return False
        elif left == None and right == None:
            return True
        # 处理节点值不同的情况
        elif left.val != right.val:
            return False
        
        # 递归比较外侧和内侧
        outside = self.compare(left.left, right.right)  # 左子树的左节点和右子树的右节点
        inside = self.compare(left.right, right.left)  # 左子树的右节点和右子树的左节点
        return outside and inside  # 两者都需要为真，整体才对称

版本二 迭代法 使用队列

实现思路：使用队列实现层序遍历，同时比较两个节点，以确保它们是对称的。每次从队列中取两个节点进行比较，然后按相应的对称顺序将它们的子节点加入队列。

import collections
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True  # 如果根节点为空，树自然对称
        queue = collections.deque()
        # 初始化队列，加入根节点的左右子节点
        queue.append(root.left)
        queue.append(root.right)
        while queue:
            leftNode = queue.popleft()
            rightNode = queue.popleft()
            # 如果左右节点同时为空，对称，继续循环
            if not leftNode and not rightNode:
                continue
            # 如果一个为空另一个不为空，或值不同，则不对称
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            # 将子节点按对称位置加入队列
            queue.append(leftNode.left)
            queue.append(rightNode.right)
            queue.append(leftNode.right)
            queue.append(rightNode.left)
        return True
        

版本三 迭代法 使用栈

实现思路：类似于使用队列的方法，但这里使用栈来存储节点。这种方法同样需要成对地取出节点进行比较，并将子节点按对称顺序推入栈中。

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True  # 如果根节点为空，树自然对称
        st = []  # 使用栈来存储节点
        st.append(root.left)
        st.append(root.right)
        while st:
            rightNode = st.pop()
            leftNode = st.pop()
            # 如果左右节点同时为空，对称，继续循环
            if not leftNode and not rightNode:
                continue
            # 如果一个为空另一个不为空，或值不同，则不对称
            if not leftNode or not rightNode or leftNode.val != rightNode.val:
                return False
            # 将子节点按对称位置加入栈
            st.append(leftNode.left)
            st.append(rightNode.right)
            st.append(leftNode.right)
            st.append(rightNode.left)
        return True
        

版本四 层次遍历

实现思路：这个方法利用层次遍历来检查每一层是否对称。将每层的节点值收集到列表中，然后检查这个列表是否与其逆序相同。这确保了每层都是对称的，从而保证了整棵树的对称性。

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        if not root:
            return True  # 如果根节点为空，树自然对称
        
        queue = collections.deque([root.left, root.right])
        
        while queue:
            level_size = len(queue)  # 当前层的节点数
            
            # 如果节点数为奇数，不能对称
            if level_size % 2 != 0:
                return False
            
            level_vals = []  # 存储当前层的节点值
            for i in range(level_size):
                node = queue.popleft()
                if node:
                    level_vals.append(node.val)
                    queue.append(node.left)
                    queue.append(node.right)
                else:
                    level_vals.append(None)
                    
            # 检查当前层的节点值列表是否对称
            if level_vals != level_vals[::-1]:
                return False
            
        return True

力扣题目链接
题目文章讲解
题目视频讲解

三、 力扣104. 二叉树的最大深度

给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 ：
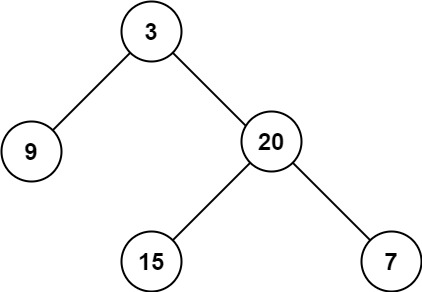
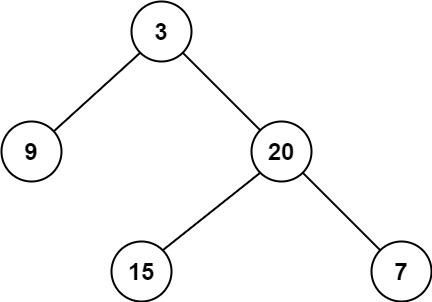
输入： root = [3,9,20,null,null,15,7]
输出： 3

版本一 递归法

实现思路：通过递归的方式，自底向上计算每个节点的最大深度，直到根节点。这种方法利用了树的后序遍历（左右中）的特点。

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        # 调用辅助函数来递归地求深度
        return self.getDepth(root)
        
    def getDepth(self, node):
        # 如果节点为空，深度为0
        if not node:
            return 0
        # 递归求左子树的深度
        leftHeight = self.getDepth(node.left)
        # 递归求右子树的深度
        rightHeight = self.getDepth(node.right)
        # 当前节点的深度是左右子树深度的最大值加1（加的1是当前节点这一层）
        height = 1 + max(leftHeight, rightHeight)
        return height

版本二 递归法 精简代码

实现思路：这是递归法的一个更简洁的版本，直接在返回时计算深度。它避免了使用额外的辅助函数，但本质上与第一个递归方法相同。

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        # 如果根节点为空，返回深度0
        if not root:
            return 0
        # 递归地计算左右子树的深度，并取最大值，然后加1代表当前层的深度
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

版本三 层序遍历迭代法

实现思路：通过层序遍历（广度优先遍历）计算树的深度。这种方法使用队列存储每一层的所有节点，每处理完一层，深度计数器加1。这个方法非常适合迭代地处理树的层级结构。

import collections

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0  # 如果树为空，深度为0
        
        depth = 0  # 初始化深度为0
        queue = collections.deque([root])  # 使用队列存储每一层的节点
        
        while queue:
            depth += 1  # 每遍历一层，深度加1
            for _ in range(len(queue)):  # 遍历当前层的所有节点
                node = queue.popleft()  # 取出节点
                if node.left:  # 如果有左子节点，加入队列
                    queue.append(node.left)
                if node.right:  # 如果有右子节点，加入队列
                    queue.append(node.right)
        
        return depth  # 遍历结束后返回深度

力扣题目链接
题目文章讲解
题目视频讲解

四、 力扣111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。
示例 ：

输入： root = [3,9,20,null,null,15,7]
输出： 2

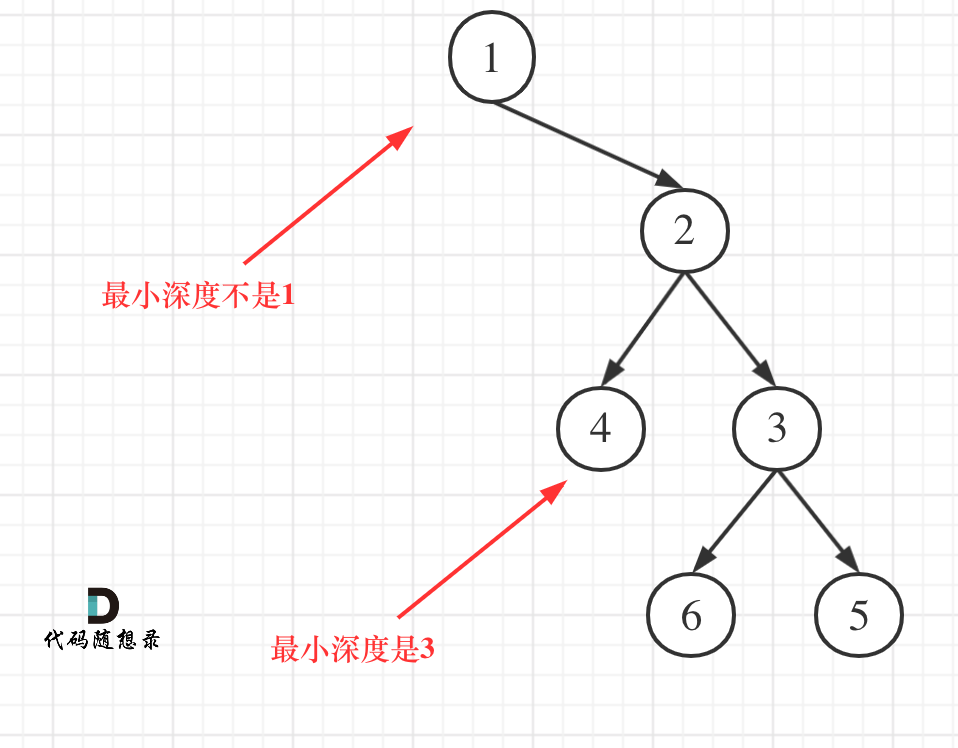
本题有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解，如图：

这就重新审题了，题目中说的是：最小深度是从根节点到最近叶子节点的最短路径上的节点数量。注意是叶子节点。

什么是叶子节点，左右孩子都为空的节点才是叶子节点！

版本一 递归法

实现思路：此方法递归地计算左右子树的深度，并在存在子树时考虑只有单侧子树的情况，确保只计算到叶子节点的深度。

class Solution:
    def getDepth(self, node):
        if node is None:
            return 0  # 空节点的深度为0
        leftDepth = self.getDepth(node.left)  # 递归求左子树的深度
        rightDepth = self.getDepth(node.right)  # 递归求右子树的深度
        
        # 如果左子树为空而右子树不为空，只计算右子树的深度
        if node.left is None and node.right is not None:
            return 1 + rightDepth
        
        # 如果右子树为空而左子树不为空，只计算左子树的深度
        if node.left is not None and node.right is None:
            return 1 + leftDepth
        
        # 如果两个子树都不为空，取两者的最小值
        result = 1 + min(leftDepth, rightDepth)
        return result

    def minDepth(self, root):
        return self.getDepth(root)

版本二 递归法 前序

实现思路：这种方法维护一个类成员变量 result 存储最小深度，通过前序遍历逐节点检查更新最小值。

class Solution:
    def __init__(self):
        self.result = float('inf')  # 初始化最小深度为无穷大

    def getDepth(self, node, depth):
        if node is None:
            return
        if node.left is None and node.right is None:
            # 更新最小深度
            self.result = min(self.result, depth)
        # 递归访问左子树
        if node.left:
            self.getDepth(node.left, depth + 1)
        # 递归访问右子树
        if node.right:
            self.getDepth(node.right, depth + 1)

    def minDepth(self, root):
        if root is None:
            return 0
        self.getDepth(root, 1)
        return self.result

版本三 迭代法

实现思路：使用队列进行层序遍历，每遍历完一层深度加一。当遇到第一个叶子节点时，返回当前深度。

import collections

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        if not root:
            return 0  # 空树的深度为0
        depth = 0
        queue = collections.deque([root])  # 使用队列进行层序遍历
        
        while queue:
            depth += 1  # 层次深度
            for _ in range(len(queue)):  # 处理当前层的所有节点
                node = queue.popleft()
                
                # 检查是否到达叶子节点
                if not node.left and not node.right:
                    return depth
            
                # 将子节点加入队列
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

        return depth

力扣题目链接
题目文章讲解
题目视频讲解