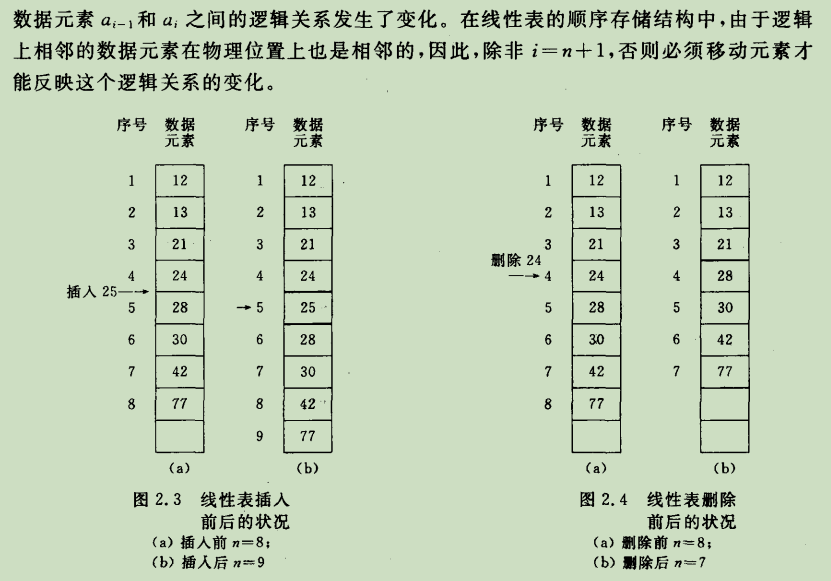
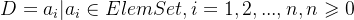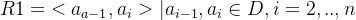数据结构(C语言版）-第二章线性表

线性数据结构的特点

线性结构是数据结构中的一种基本类型，其特点是数据元素之间存在一对一的线性关系，即每个元素（除了第一个和最后一个）都有一个前驱元素和一个后继元素。线性结构的主要特点包括：

1. 顺序性：线性结构中的元素按照一定的顺序排列，这个顺序可以是逻辑上的也可以是物理存储上的顺序。
2. 访问方式：线性结构支持顺序访问和随机访问（如果数据是连续存储的话）。顺序访问是指从结构的一个端点开始，逐个访问每一个元素直到另一个端点。对于某些线性结构，如数组，还可以通过索引直接访问任意位置的元素。
3. 操作简单：线性结构的基本操作如插入、删除、查找等通常相对容易实现，尤其是当数据是顺序存储时。
4. 结构清晰：线性结构的逻辑关系直观明了，便于理解和操作。

常见的线性结构包括：

- 数组 (Array): 元素在内存中连续存储，每个元素可以通过索引快速访问，但插入和删除操作可能较慢，因为可能需要移动大量元素。
- 链表 (Linked List): 元素在内存中可以不连续存储，每个元素包含指向下一个元素的指针（单链表），或者同时包含指向前一个和后一个元素的指针（双链表）。链表的插入和删除操作较快，但随机访问较慢。
- 栈 (Stack): 后进先出（LIFO, Last In First Out）的线性结构，主要操作是压栈（push）和弹栈（pop）。
- 队列 (Queue): 先进先出（FIFO, First In First Out）的线性结构，主要操作是入队（enqueue）和出队（dequeue）。
- 循环队列 (Circular Queue): 队列的一种变体，尾部连接到头部形成环状，可以更高效地利用存储空间。
- 字符串 (String): 一种特殊的线性结构，元素为字符，常用于文本处理。
线性结构因其简单性和普遍适用性，在算法和数据结构中占据重要地位。

2. 1 线性表的类型定义

ADT List {

数据对象： $D={a_{i}| a_{i}\in ElemSet, i=1,2,...,n, n\geqslant 0}$

数据关系： $R1 = {<a_{a-1}, a_{i} >|a_{i-1}, a_{i}\in D,i=2,..,n}$

基本操作：

InitList(&L)

操作结果：构造一个空的线性表L

DestroyList(&L)

初始条件：线性表L已存在。

操作结果，销毁线性表L。

ClearList (&L)

初始条件：线性表L巳存在。

操作结果：将L重置为空表。

ListEmpty(L)

初始条件：线性表L已存在。

操作结果：若L为空表，则返回 TRUE, 否则返回 FALSE。

ListLength(L)

初始条件：线性表L已存在。

操作结果：返回L中数据元素个数。

GetElem(L, i, &e)

初始条件：线性表已存在， 1 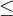$\leq$ i $\leqslant$ ListLength(L)

操作结果：用e返回L中第i个数据元素的值。

LocateElem(L, e, compare())

初始条件：线性表L已存在， compare() 是数据元素判定函数。

操作结果：返回中第个与满足关系 compare() 的数据元素的位序。若这样的数据元素不存在，则返回值为 o.

PriorElem(L, cur-e, &pre-e)

初始条件：线性表L已存在。

操作结果：若 cur-e 的数据元素，且不是第一个，则用 pre-e返回它的前驱，否则操作失败， pre_ 无定义。

NextElem(L, cur-e, &next-e)

初始条件：线性表L已存在。

操作结果：若 cur-e是L的数据元素，且不是最后一个，则用 next-e 返回它的后继，否则操作失败， next-e无定义。

Listinser (&L, i, e)

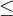
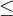
初始条件：线性表L已存在， l $\leq$ i $\leq$ ListLength(L) +1。

操作结果，在L中第i个位置之前插入新的数据元素 e,L 的长度加1。

ListDelete(&L, i, &e)

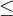
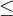
初始条件：线性表L已存在且非空， l $\leq$ i $\leq$ ListLength(L)

操作结果：删除L的第个数据元素，并用e返回其值，L的长度减1。

ListTraverse(L, visit（））

初始条件：线性表L已存在。

操作结果：依次对L的每个数据元素调用函数 visit（）。一旦 visit() 失败，则操作失败。

} ADT List

例2-1 求两个集合的并集

假设利用两个线性表 LA LB 分别表示两个集合 B( 即线性表中的数据元素即为集合中的成员），现要求一个新的集合 A=AUB 。这就要求对线性表作如下操作：扩大线性表 LA, 将存在千线性表 LB 中而不存在于线性表 LA 中的数据元素插入到线性表 LA 中去。只要从线性表 LB 中依次取得每个数据元素，并依值在线性表 LA 进行查访，若不存在，则插入之。上述操作过程可用下列算法描述之。

#include <stdio.h>
#define MAX_ELEMENTS 100 // 假设最大元素数量不超过这个值

// 函数用于打印集合
void printArray(int arr[], int size) {
    for(int i = 0; i < size; ++i)
        printf("%d ", arr[i]);
    printf("\n");
}

// 函数用于求两个线性表的并集
int unionOfArrays(int LA[], int sizeLA, int LB[], int sizeLB, int result[]) {
    int indexResult = 0; // 并集数组当前索引
    int i, j;

    // 将LA数组的所有元素加入到result中
    for(i = 0; i < sizeLA; ++i)
        result[indexResult++] = LA[i];

    // 检查LB中的每个元素是否已存在于result中，若不存在则添加
    for(i = 0; i < sizeLB; ++i) {
        int exists = 0;
        for(j = 0; j < indexResult; ++j) {
            if(LB[i] == result[j]) {
                exists = 1;
                break;
            }
        }
        if(!exists) // 如果LB中的元素不在result中，则加入
            result[indexResult++] = LB[i];
    }

    return indexResult; // 返回并集数组的实际大小
}

int main() {
    int LA[] = {1, 2, 3, 4};
    int LB[] = {3, 4, 5, 6};
    int A[MAX_ELEMENTS]; // 用于存放并集

    int sizeLA = sizeof(LA)/sizeof(LA[0]);
    int sizeLB = sizeof(LB)/sizeof(LB[0]);

    int unionSize = unionOfArrays(LA, sizeLA, LB, sizeLB, A);
    printf("Union of LA and LB is: ");
    printArray(A, unionSize);

    return 0;
}

原文抽象代码

算法2.1

例2-2 线性表合并有序排列

已知线性表 LA LB 中的数据元素按值非递减有序排列，现要求将 LA, LB 归并为一个新的线性表 LC, LC 中的数据元素仍按值非递减有序排列。例如，设

LA= (3,5,8,11)

LB= (2,6,8,9,ll,15,20)

则

LC= (2,3,5,6,8,8,9,ll,ll,15,20)

#include <stdio.h>
#define MAX_ELEMENTS 100

// 函数用于打印线性表
void printList(int list[], int size)
{
    for (int i = 0; i < size; ++i)
        printf("%d ", list[i]);
    printf("\n");
}

// 函数用于合并两个有序线性表为一个新的有序线性表
int mergeSortedLists(int LA[], int sizeLA, int LB[], int sizeLB, int LC[])
{
    int i = 0, j = 0, k = 0; // 初始化三个指针

    // 遍历两个列表，直到一个列表结束
    while (i < sizeLA && j < sizeLB)
    {
        if (LA[i] <= LB[j])
        {
            LC[k++] = LA[i++];
        }
        else
        {
            LC[k++] = LB[j++];
        }
    }

    // 如果LA还有剩余元素，直接拷贝到LC
    while (i < sizeLA)
    {
        LC[k++] = LA[i++];
    }

    // 如果LB还有剩余元素，直接拷贝到LC
    while (j < sizeLB)
    {
        LC[k++] = LB[j++];
    }

    return k; // 返回新列表的实际大小
}

int main()
{
    int LA[] = {3, 5, 8, 11};
    int LB[] = {2, 6, 8, 9, 11, 15, 20};
    int LC[MAX_ELEMENTS]; // 假设MAX_ELEMENTS足够大以容纳合并后的列表

    int sizeLA = sizeof(LA) / sizeof(LA[0]);
    int sizeLB = sizeof(LB) / sizeof(LB[0]);

    int newSize = mergeSortedLists(LA, sizeLA, LB, sizeLB, LC);
    printf("Merged list LC is: ");
    printList(LC, newSize);

    return 0;
}

原文抽象代码

算法2.2

2. 2 线性表的顺序表示和实现

算法2.3-扩容添加元素

例如，图 2.3 表示一个线性表在进行插入操作的前、后，其数据元素在存储空间中的位置变化。为了在线性表的第和第个元素之间插入一个值为 25 的数据元素，则需将第五个至第个数据元素依次往后移动一个位置。

一般情况下，在第 i(l~i~n) 个元素之前插入一个元素时，需将第至第 i( n-i+ 1) 个元素向后移动一个位置，如算法 2.4 所示。

可执行代码案例

#include <stdio.h>
#include <stdlib.h>
#include <string.h> // 用于memset

typedef struct
{
    int *data;    // 动态数组
    int capacity; // 当前容量
    int size;     // 当前元素数量
} LinearList;

// 初始化线性表
LinearList *initLinearList()
{
    LinearList *list = (LinearList *)malloc(sizeof(LinearList));
    list->data = (int *)calloc(10, sizeof(int)); // 初始容量设为10
    list->capacity = 10;
    list->size = 0;
    return list;
}

// 销毁线性表
void destroyLinearList(LinearList *list)
{
    free(list->data);
    free(list);
}

// 扩容函数
void resizeLinearList(LinearList *list)
{
    int newCapacity = list->capacity * 2; // 扩容为原来的两倍
    list->data = (int *)realloc(list->data, newCapacity * sizeof(int));
    list->capacity = newCapacity;
}

void insertAt(LinearList *list, int index, int value)
{
    if (list->size == list->capacity)
    {
        resizeLinearList(list); // 先检查是否需要扩容
    }

    // 特殊处理：如果要插入到空列表或索引0，直接添加在最前面
    if (list->size == 0 || index == 0)
    {
        memmove(&list->data[1], &list->data[0], list->size * sizeof(int)); // 移动现有元素
        list->data[0] = value;                                             // 插入新元素
    }
    else if (index <= list->size)
    {                                                                                            // 对于其他合法索引
        memmove(&list->data[index + 1], &list->data[index], (list->size - index) * sizeof(int)); // 移动元素
        list->data[index] = value;                                                               // 插入新元素
    }
    else
    {
        printf("Index out of bounds.\n");
        return;
    }
    list->size++; // 无论哪种情况，插入后元素数量都要增加
}

// 打印线性表
void printLinearList(const LinearList *list)
{
    for (int i = 0; i < list->size; ++i)
    {
        printf("%d ", list->data[i]);
    }
    printf("\n");
}

int main()
{
    LinearList *list = initLinearList();

    // 添加更多元素以展示扩容
    for (int i = 0; i < 20; ++i)
    {
        insertAt(list, list->size, i);
    }

    // 示例：在索引为1的位置插入数字7
    insertAt(list, 1, 77);

    printLinearList(list); // 打印线性表

    destroyLinearList(list);
    return 0;
}

算法2. 4 -固定大小的线性表删除元素

算法2.5 (略)

算法2.6 (顺序表合并)

#include <stdio.h>
#include <stdlib.h>
#include <string.h> // 用于memset

// 函数声明
void mergeSortedArrays(int arr1[], int size1, int arr2[], int size2, int mergedArr[]);
void printArray(int arr[], int size);

int main() {
    int arr1[] = {1, 3, 5, 7};
    int arr2[] = {2, 4, 6, 8};
    int size1 = sizeof(arr1) / sizeof(arr1[0]);
    int size2 = sizeof(arr2) / sizeof(arr2[0]);
    
    int mergedSize = size1 + size2;
    int mergedArr[mergedSize];
    
    mergeSortedArrays(arr1, size1, arr2, size2, mergedArr);
    
    printf("Merged array: ");
    printArray(mergedArr, mergedSize);
    
    return 0;
}

// 合并两个有序数组的函数
void mergeSortedArrays(int arr1[], int size1, int arr2[], int size2, int mergedArr[]) {
    int i = 0, j = 0, k = 0;
    
    // 遍历两个数组，直到一个数组遍历完
    while (i < size1 && j < size2) {
        if (arr1[i] <= arr2[j]) {
            mergedArr[k++] = arr1[i++];
        } else {
            mergedArr[k++] = arr2[j++];
        }
    }
    
    // 如果arr1还有剩余元素，直接复制到mergedArr
    while (i < size1) {
        mergedArr[k++] = arr1[i++];
    }
    
    // 如果arr2还有剩余元素，直接复制到mergedArr
    while (j < size2) {
        mergedArr[k++] = arr2[j++];
    }
}

// 打印数组的函数
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

算法2. 7 (略)

2. 3 线性表的链式表示和实现

2.3.1 线性链表

带头链表的单链表的实现

算法2.8(插入第i个节点) | 算法2.9(删除第i个节点) |算法2.10(头插法)|算法2.11(尾插发)

实现一个带头结点的单链表通常涉及以下几个步骤：

定义节点结构体；
初始化链表；
插入节点（头插法、尾插法）；
删除节点（删除头结点后的第一个节点、删除指定节点）；
遍历和显示链表；
销毁链表。

带头结点的单链表实现的例子：

#include <stdio.h>
#include <stdlib.h>

// 定义节点结构体
typedef struct Node {
    int data;
    struct Node *next;
} Node;

// 定义链表类型
typedef struct LinkList {
    Node *head; // 指向链表的头结点
} LinkList;

// 初始化链表
void InitList(LinkList *L) {
    L->head = (Node *)malloc(sizeof(Node));
    if (!L->head) {
        printf("Memory allocation failed.\n");
        exit(EXIT_FAILURE);
    }
    L->head->next = NULL; // 头结点的next置空
}

// 头插法插入节点
void InsertToHead(LinkList *L, int data) {
    Node *new_node = (Node *)malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        exit(EXIT_FAILURE);
    }
    new_node->data = data;
    new_node->next = L->head->next;
    L->head->next = new_node;
}

// 尾插法插入节点
void InsertToTail(LinkList *L, int data) {
    Node *new_node = (Node *)malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        exit(EXIT_FAILURE);
    }
    new_node->data = data;
    new_node->next = NULL;
    
    Node *p = L->head;
    while (p->next != NULL) {
        p = p->next;
    }
    p->next = new_node;
}

// 添加到第i个位置
void InsertToIndex(LinkList *L, int index, int data) {
    if (index <= 0) {
        printf("Invalid index.\n");
        return;
    }
    
    Node *new_node = (Node *)malloc(sizeof(Node));
    if (!new_node) {
        printf("Memory allocation failed.\n");
        exit(EXIT_FAILURE);
    }
    new_node->data = data;
    
    Node *p = L->head;
    for (int i = 0; i < index - 1 && p->next != NULL; i++) {
        p = p->next;
    }
    if (p->next == NULL && index > 1) {
        printf("Index out of range.\n");
        free(new_node);
        return;
    }
    
    new_node->next = p->next;
    p->next = new_node;
}

//删除第i个位置
void DeleteFromIndex(LinkList *L, int index) {
    if (index <= 0) {
        printf("Invalid index.\n");
        return;
    }
    
    Node *p = L->head;
    for (int i = 0; i < index - 1 && p->next != NULL; i++) {
        p = p->next;
    }
    if (p->next == NULL) {
        printf("Index out of range.\n");
        return;
    }
    
    Node *del_node = p->next;
    p->next = del_node->next;
    free(del_node);
}

// 打印链表
void PrintList(LinkList *L) {
    Node *p = L->head->next;
    while (p != NULL) {
        printf("%d -> ", p->data);
        p = p->next;
    }
    printf("NULL\n");
}

// 销毁链表
void DestroyList(LinkList *L) {
    Node *p = L->head;
    while (p != NULL) {
        Node *temp = p;
        p = p->next;
        free(temp);
    }
    L->head = NULL;
}

int main() {
    LinkList L;
    InitList(&L);
    
    // 插入一些节点
    InsertToHead(&L, 3);
    InsertToHead(&L, 2);
    InsertToHead(&L, 1);
    InsertToTail(&L, 4);
    InsertToTail(&L, 5);
    
    // 打印链表
    PrintList(&L);
    
    // 销毁链表
    DestroyList(&L);
    
    return 0;
}

算法 2.12 (静态链表实现)

#include <stdio.h>

#define MAX_SIZE 100 // 定义静态链表的最大长度

typedef struct {
    int data; // 数据部分
    int next; // 下一个节点的索引，如果是最后一个节点，则设置为 -1
} Node;

Node list[MAX_SIZE]; // 静态链表数组
int head = -1; // 链表头的索引，初始为 -1 表示链表为空
int free = 0; // 第一个可用位置的索引，即自由链表的头

// 初始化静态链表
void initStaticList() {
    for (int i = 0; i < MAX_SIZE - 1; i++) {
        list[i].next = i + 1;
    }
    list[MAX_SIZE - 1].next = -1; // 最后一个元素的 next 设置为 -1
    head = -1;
    free = 0;
}

// 插入节点到链表头部
void insertAtHead(int data) {
    if (free == -1) {
        printf("No space left in the list.\n");
        return;
    }
    
    int newNode = free; // 获取新的节点索引
    free = list[free].next; // 更新自由链表的头
    
    list[newNode].data = data; // 设置新节点的数据
    list[newNode].next = head; // 新节点的 next 指向原链表头
    head = newNode; // 更新链表头
}

// 遍历并打印链表
void printList() {
    int p = head;
    while (p != -1) {
        printf("%d -> ", list[p].data);
        p = list[p].next;
    }
    printf("NULL\n");
}

int main() {
    initStaticList(); // 初始化静态链表
    
    // 插入一些数据
    insertAtHead(3);
    insertAtHead(2);
    insertAtHead(1);
    insertAtHead(4);
    
    // 打印链表
    printList();
    
    return 0;
}

算法 2.14：判断单链表是否为空 |2.15：清空单链表|2.16：求单链表的表长|2.17：在单链表的第 i 个位置插入元素 e

#include <stdio.h>
#include <stdlib.h>

// 链表节点结构体
typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

// 算法 2.13：初始化一个空的单链表
void InitList(LinkList *L) {
    *L = (LinkList)malloc(sizeof(LNode));
    if (*L == NULL) {
        printf("内存分配失败\n");
        return;
    }
    (*L)->next = NULL;
}

// 算法 2.14：判断单链表是否为空
int ListEmpty(LinkList L) {
    return L->next == NULL;
}

// 算法 2.15：清空单链表
void ClearList(LinkList *L) {
    LinkList p, q;
    p = (*L)->next;
    while (p!= NULL) {
        q = p->next;
        free(p);
        p = q;
    }
    (*L)->next = NULL;
}

// 算法 2.16：求单链表的表长
int ListLength(LinkList L) {
    int count = 0;
    LinkList p = L->next;
    while (p!= NULL) {
        count++;
        p = p->next;
    }
    return count;
}

// 算法 2.17：在单链表的第 i 个位置插入元素 e
int ListInsert(LinkList L, int i, int e) {
    int j = 0;
    LinkList p = L, s;
    while (p!= NULL && j < i - 1) {
        p = p->next;
        j++;
    }
    if (p == NULL || j > i - 1) {
        printf("插入位置不合法\n");
        return 0;
    }
    s = (LinkList)malloc(sizeof(LNode));
    if (s == NULL) {
        printf("内存分配失败\n");
        return 0;
    }
    s->data = e;
    s->next = p->next;
    p->next = s;
    return 1;
}

int main() {
    LinkList L;

    // 初始化单链表
    InitList(&L);

    // 判断单链表是否为空
    if (ListEmpty(L)) {
        printf("single linkList is empty\n");
    } else {
        printf("single linkList is not empty\n");
    }

    // 插入元素
    ListInsert(L, 1, 10);
    ListInsert(L, 2, 20);
    ListInsert(L, 3, 30);

    // 求单链表的表长
    int length = ListLength(L);
    printf("single linkList length is %d\n", length);

    // 清空单链表
    ClearList(&L);

    return 0;
}

2. 3. 2 循环链表

循环链表（Circular Linked List）

循环链表是一种特殊的链表，它的特点是链表中最后一个节点的指针不是指向空，而是指向链表的头节点，从而使整个链表形成一个环。

优点：

从循环链表中的任何一个节点出发，都可以找到链表中的其他节点，这使得一些操作（如遍历整个链表）更加方便。
在某些应用中，如约瑟夫问题等，循环链表比普通链表更适合。

实现：
循环链表的实现与普通链表类似，只是在创建链表和一些操作上需要注意形成循环。

#include <stdio.h>
#include <stdlib.h>

// 链表节点结构体
typedef struct ListNode {
    int data;
    struct ListNode *next;
} ListNode;

// 创建循环链表节点
ListNode* createNode(int data) {
    ListNode* newNode = (ListNode*)malloc(sizeof(ListNode));
    if (newNode == NULL) {
        printf("Memory allocation failed\n");
        return NULL;
    }
    newNode->data = data;
    newNode->next = NULL;
    return newNode;
}

// 插入节点到循环链表头部
void insertAtHead(ListNode** head, int data) {
    ListNode* newNode = createNode(data);
    if (*head == NULL) {
        // 如果链表为空，新节点就是唯一的节点，形成循环
        newNode->next = newNode;
        *head = newNode;
    } else {
        ListNode* temp = *head;
        while (temp->next!= *head) {
            temp = temp->next;
        }
        // 将新节点插入到头部，并更新循环
        newNode->next = *head;
        temp->next = newNode;
        *head = newNode;
    }
}

// 打印循环链表
void printList(ListNode* head) {
    if (head == NULL) {
        printf("The linked list is empty\n");
        return;
    }
    ListNode* temp = head;
    do {
        printf("%d ", temp->data);
        temp = temp->next;
    } while (temp!= head);
    printf("\n");
}

// 释放循环链表内存
void freeList(ListNode* head) {
    if (head == NULL) {
        return;
    }
    ListNode* curr = head;
    ListNode* next;
    do {
        next = curr->next;
        free(curr);
        curr = next;
    } while (curr!= head);
}

int main() {
    ListNode* head = NULL;

    insertAtHead(&head, 1);
    insertAtHead(&head, 2);
    insertAtHead(&head, 3);

    printf("Circular Linked List: ");
    printList(head);

    freeList(head);

    return 0;
}

createNode 函数用于创建一个新的链表节点，并初始化其数据和指针。
insertAtHead 函数用于将一个新节点插入到循环链表的头部。如果链表为空，新节点自己形成一个循环；否则，将新节点插入到头部，并更新循环关系。
printList 函数用于打印循环链表的内容。通过一个 do-while 循环来实现，确保至少打印一次（因为循环链表的头部是确定的，即使链表只有一个节点也能正确打印）。
freeList 函数用于释放循环链表的内存，通过一个 do-while 循环依次释放每个节点的内存。

2. 3. 2 双向链表

双向链表定义

双向链表是一种链式存储结构，其中每个节点包含三个部分：

数据域：用于存储实际的数据信息。
前驱指针（Prev）：指向其前一个节点的指针。
后继指针（Next）：指向其后一个节点的指针。

这种结构使得双向链表上的节点可以向前和向后移动，提供了比单链表更灵活的访问能力。

特点

双向性：由于每个节点都保存了前后节点的信息，所以在双向链表中可以很容易地从前向后或从后向前遍历链表。
插入和删除操作：插入或删除一个节点时，需要同时更新被操作节点的前驱和后继节点的指针，因此相比单链表，双向链表的这些操作稍微复杂一些，但并不增加算法的时间复杂度。

#include <stdio.h>
#include <stdlib.h>

// 双向链表节点结构体
typedef struct DuLNode {
    int data;
    struct DuLNode *prior;
    struct DuLNode *next;
} DuLNode, *DuLinkList;

// 创建双向链表节点
DuLNode* createDuLNode(int data) {
    DuLNode* newNode = (DuLNode*)malloc(sizeof(DuLNode));
    if (newNode == NULL) {
        printf("Memory allocation failed\n");
        return NULL;
    }
    newNode->data = data;
    newNode->prior = NULL;
    newNode->next = NULL;
    return newNode;
}

// 在双向链表头部插入节点
void insertAtHead(DuLinkList *L, int data) {
    DuLNode* newNode = createDuLNode(data);
    if (*L == NULL) {
        // 如果链表为空，新节点即为链表的唯一节点
        *L = newNode;
        newNode->prior = newNode;
        newNode->next = newNode;
    } else {
        // 将新节点插入到头部
        newNode->next = *L;
        newNode->prior = (*L)->prior;
        (*L)->prior->next = newNode;
        (*L)->prior = newNode;
        *L = newNode;
    }
}

// 打印双向链表
void printDuLinkList(DuLinkList L) {
    if (L == NULL) {
        printf("The doubly linked list is empty\n");
        return;
    }
    DuLNode* curr = L;
    printf("Doubly Linked List: ");
    do {
        printf("%d ", curr->data);
        curr = curr->next;
    } while (curr!= L);
    printf("\n");
}

// 释放双向链表内存
void freeDuLinkList(DuLinkList L) {
    if (L == NULL) {
        return;
    }
    DuLNode* curr = L;
    DuLNode* temp;
    do {
        temp = curr;
        curr = curr->next;
        free(temp);
    } while (curr!= L);
}

int main() {
    DuLinkList L = NULL;

    insertAtHead(&L, 10);
    insertAtHead(&L, 20);
    insertAtHead(&L, 30);

    printDuLinkList(L);

    freeDuLinkList(L);

    return 0;
}

createDuLNode 函数用于创建一个新的双向链表节点，并进行内存分配和数据初始化。
insertAtHead 函数用于在双向链表的头部插入一个新节点。如果链表为空，新节点成为唯一节点，并建立双向循环链接；否则，将新节点插入到头部，并更新前后节点的链接关系。
printDuLinkList 函数用于打印双向链表的内容。如果链表为空，输出相应提示信息；否则，从头部开始遍历链表并打印每个节点的数据。
freeDuLinkList 函数用于释放双向链表的内存空间。通过遍历链表，依次释放每个节点的内存。

算法 2.18：取第 i 个元素|算法 2.19：在第 i 个位置插入元素 e|算法 2.20：删除第 i 个元素，并将其值赋给 e|算法 2.21：合并两个有序链表 La 和 Lb 为一个新的有序链表 Lc

#include <stdio.h>
#include <stdlib.h>

// 链表节点结构体
typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

// 算法 2.18：取第 i 个元素
int GetElem(LinkList L, int i, int *e) {
    int j = 1;
    LinkList p = L->next;
    while (p!= NULL && j < i) {
        p = p->next;
        j++;
    }
    if (p == NULL || j > i) {
        return 0;
    }
    *e = p->data;
    return 1;
}

// 算法 2.19：在第 i 个位置插入元素 e
int ListInsert(LinkList *L, int i, int e) {
    int j = 1;
    LinkList p = *L, s;
    while (p!= NULL && j < i - 1) {
        p = p->next;
        j++;
    }
    if (p == NULL || j > i - 1) {
        return 0;
    }
    s = (LinkList)malloc(sizeof(LNode));
    if (s == NULL) {
        return 0;
    }
    s->data = e;
    s->next = p->next;
    p->next = s;
    return 1;
}

// 算法 2.20：删除第 i 个元素，并将其值赋给 e
int ListDelete(LinkList *L, int i, int *e) {
    int j = 1;
    LinkList p = *L, q;
    while (p->next!= NULL && j < i) {
        p = p->next;
        j++;
    }
    if (p->next == NULL || j > i) {
        return 0;
    }
    q = p->next;
    p->next = q->next;
    *e = q->data;
    free(q);
    return 1;
}

// 算法 2.21：合并两个有序链表 La 和 Lb 为一个新的有序链表 Lc
LinkList MergeList(LinkList La, LinkList Lb) {
    LinkList Lc, pa, pb, pc;
    Lc = (LinkList)malloc(sizeof(LNode));
    pc = Lc;
    pa = La->next;
    pb = Lb->next;
    while (pa!= NULL && pb!= NULL) {
        if (pa->data <= pb->data) {
            pc->next = pa;
            pc = pa;
            pa = pa->next;
        } else {
            pc->next = pb;
            pc = pb;
            pb = pb->next;
        }
    }
    if (pa!= NULL) {
        pc->next = pa;
    }
    if (pb!= NULL) {
        pc->next = pb;
    }
    free(La);
    free(Lb);
    return Lc;
}

// 打印链表函数
void PrintList(LinkList L) {
    LinkList p = L->next;
    while (p!= NULL) {
        printf("%d ", p->data);
        p = p->next;
    }
    printf("\n");
}

int main() {
    // 构建测试链表 La
    LinkList La = (LinkList)malloc(sizeof(LNode));
    La->next = NULL;
    ListInsert(&La, 1, 1);
    ListInsert(&La, 2, 3);
    ListInsert(&La, 3, 5);

    // 构建测试链表 Lb
    LinkList Lb = (LinkList)malloc(sizeof(LNode));
    Lb->next = NULL;
    ListInsert(&Lb, 1, 2);
    ListInsert(&Lb, 2, 4);
    ListInsert(&Lb, 3, 6);

    printf("链表 La: ");
    PrintList(La);
    printf("链表 Lb: ");
    PrintList(Lb);

    // 测试算法 2.18：取第 2 个元素
    int e;
    if (GetElem(La, 2, &e)) {
        printf("链表 La 中第 2 个元素为: %d\n", e);
    } else {
        printf("获取元素失败\n");
    }

    // 测试算法 2.19：在第 4 个位置插入元素 7
    if (ListInsert(&La, 4, 7)) {
        printf("在链表 La 中第 4 个位置插入元素 7 成功\n");
    } else {
        printf("插入元素失败\n");
    }

    printf("插入元素后的链表 La: ");
    PrintList(La);

    // 测试算法 2.20：删除第 3 个元素
    if (ListDelete(&La, 3, &e)) {
        printf("从链表 La 中删除第 3 个元素 %d 成功\n", e);
    } else {
        printf("删除元素失败\n");
    }

    printf("删除元素后的链表 La: ");
    PrintList(La);

    // 测试算法 2.21：合并链表 La 和 Lb 为 Lc
    LinkList Lc = MergeList(La, Lb);
    printf("合并后的链表 Lc: ");
    PrintList(Lc);

    return 0;
}

2.4 一元多项式的表示及相加

一元多项式的表示

在数学中，一元多项式可以表示为：

$\rho _{_{n}}(x) = a_{n}x^{n}+a_{n-1}x^{n-1}+....+a_{1}x+a_{0}$

在计算机中，为了有效地表示和操作一元多项式，可以使用链表来实现。每个链表节点表示多项式的一项，包含系数和指数两个数据域。

多项式的相加

多项式相加的基本思想是：将两个多项式的对应项进行系数相加，如果某一项的指数在另一个多项式中不存在，则将其直接添加到结果多项式中。

具体步骤如下：

同时遍历两个待相加的多项式链表。
比较当前两个节点的指数：
- 如果指数相等，则将系数相加，创建一个新的节点并插入到结果多项式链表中，然后同时向前移动两个多项式的指针。
- 如果一个多项式的当前节点指数小于另一个多项式的当前节点指数，则将指数较小的节点插入到结果多项式链表中，并向前移动该多项式的指针。
- 如果一个多项式遍历完，而另一个多项式还有剩余节点，则将剩余节点依次插入到结果多项式链表中。

#include <stdio.h>
#include <stdlib.h>

// 多项式项的结构体
typedef struct PolyNode {
    int coef;  // 系数
    int expo;  // 指数
    struct PolyNode *next;
} PolyNode, *Polynomial;

// 创建新的多项式项节点
PolyNode *createNode(int coef, int expo) {
    PolyNode *newNode = (PolyNode *)malloc(sizeof(PolyNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        return NULL;
    }
    newNode->coef = coef;
    newNode->expo = expo;
    newNode->next = NULL;
    return newNode;
}

// 插入多项式项到链表中（按照指数降序排列）
void insertTerm(Polynomial *poly, int coef, int expo) {
    PolyNode *newNode = createNode(coef, expo);
    if (*poly == NULL) {
        // 如果链表为空，直接将新节点作为链表的头节点
        *poly = newNode;
    } else {
        PolyNode *curr = *poly;
        PolyNode *prev = NULL;
        while (curr!= NULL && curr->expo > expo) {
            prev = curr;
            curr = curr->next;
        }
        if (curr!= NULL && curr->expo == expo) {
            // 如果指数相同，系数相加
            curr->coef += coef;
            free(newNode);
            if (curr->coef == 0) {
                // 如果相加后系数为 0，删除该节点
                if (prev == NULL) {
                    *poly = curr->next;
                } else {
                    prev->next = curr->next;
                }
                free(curr);
            }
        } else {
            // 插入新节点
            if (prev == NULL) {
                newNode->next = *poly;
                *poly = newNode;
            } else {
                newNode->next = curr;
                prev->next = newNode;
            }
        }
    }
}

// 打印多项式
void printPolynomial(Polynomial poly) {
    PolyNode *curr = poly;
    while (curr!= NULL) {
        printf("%dx^%d", curr->coef, curr->expo);
        curr = curr->next;
        if (curr!= NULL) {
            printf(" + ");
        }
    }
    printf("\n");
}

// 多项式相加
Polynomial addPolynomials(Polynomial poly1, Polynomial poly2) {
    Polynomial result = NULL;
    PolyNode *p1 = poly1;
    PolyNode *p2 = poly2;

    while (p1!= NULL && p2!= NULL) {
        if (p1->expo > p2->expo) {
            insertTerm(&result, p1->coef, p1->expo);
            p1 = p1->next;
        } else if (p1->expo < p2->expo) {
            insertTerm(&result, p2->coef, p2->expo);
            p2 = p2->next;
        } else {
            int coefSum = p1->coef + p2->coef;
            insertTerm(&result, coefSum, p1->expo);
            p1 = p1->next;
            p2 = p2->next;
        }
    }

    while (p1!= NULL) {
        insertTerm(&result, p1->coef, p1->expo);
        p1 = p1->next;
    }

    while (p2!= NULL) {
        insertTerm(&result, p2->coef, p2->expo);
        p2 = p2->next;
    }

    return result;
}

// 释放多项式链表的内存
void freePolynomial(Polynomial poly) {
    PolyNode *curr = poly;
    PolyNode *next;

    while (curr!= NULL) {
        next = curr->next;
        free(curr);
        curr = next;
    }
}

int main() {
    Polynomial poly1 = NULL;
    Polynomial poly2 = NULL;

    // 构建第一个多项式：3x^4 + 2x^2 + 1
    insertTerm(&poly1, 3, 4);
    insertTerm(&poly1, 2, 2);
    insertTerm(&poly1, 1, 0);

    // 构建第二个多项式：2x^3 - 3x^2 + 5
    insertTerm(&poly2, 2, 3);
    insertTerm(&poly2, -3, 2);
    insertTerm(&poly2, 5, 0);

    printf("多项式 1: ");
    printPolynomial(poly1);

    printf("多项式 2: ");
    printPolynomial(poly2);

    Polynomial sum = addPolynomials(poly1, poly2);

    printf("相加后的结果: ");
    printPolynomial(sum);

    // 释放内存
    freePolynomial(poly1);
    freePolynomial(poly2);
    freePolynomial(sum);

    return 0;
}

算法2.22

#include <stdio.h>
#include <stdlib.h>

// 定义多项式的项的结构体
typedef struct PolynomialNode {
    int coef;  // 系数
    int expo;  // 指数
    struct PolynomialNode *next;
} PolyNode, *Polynomial;

// 获取链表头节点
Polynomial GetHead(Polynomial P) {
    return P;
}

// 获取下一个节点
Polynomial NextPos(Polynomial P, Polynomial pos) {
    return pos->next;
}

// 获取当前节点的元素值
void GetCurElem(Polynomial pos, int *coef, int *expo) {
    *coef = pos->coef;
    *expo = pos->expo;
}

// 比较两个整数
int cmp(int a, int b) {
    if (a < b) {
        return -1;
    } else if (a == b) {
        return 0;
    } else {
        return 1;
    }
}

// 设置当前节点的元素值
void SetCurElem(Polynomial pos, int coef) {
    pos->coef = coef;
}

// 删除链表中的第一个节点
void DelFirst(Polynomial head, Polynomial *pos) {
    Polynomial temp = *pos;
    *pos = (*pos)->next;
    free(temp);
}

// 在指定位置插入节点
void InsFirst(Polynomial head, Polynomial node) {
    node->next = head->next;
    head->next = node;
}

// 判断链表是否为空
int ListEmpty(Polynomial P) {
    return P->next == NULL;
}

// 将一个链表追加到另一个链表的末尾
void Append(Polynomial Pa, Polynomial Pb) {
    Polynomial p = Pa;
    while (p->next!= NULL) {
        p = p->next;
    }
    p->next = Pb->next;
    Pb->next = NULL;
}

// 释放节点内存
void FreeNode(Polynomial node) {
    free(node);
}

// 多项式加法函数
void AddPolyn(Polynomial *Pa, Polynomial *Pb) {
    Polynomial ha = GetHead(*Pa), hb = GetHead(*Pb);
    Polynomial qa = NextPos(*Pa, ha), qb = NextPos(*Pb, hb);

    while (qa && qb) {
        int a_coef, a_expo, b_coef, b_expo;
        GetCurElem(qa, &a_coef, &a_expo);
        GetCurElem(qb, &b_coef, &b_expo);

        switch (cmp(a_expo, b_expo)) {
            case -1:
                ha = qa;
                qa = NextPos(*Pa, qa);
                break;
            case 0:
                int sum = a_coef + b_coef;
                if (sum!= 0) {
                    SetCurElem(qa, sum);
                    ha = qa;
                } else {
                    DelFirst(ha, &qa);
                    FreeNode(qa);
                }
                DelFirst(hb, &qb);
                FreeNode(qb);
                qa = NextPos(*Pa, ha);
                qb = NextPos(*Pb, hb);
                break;
            case 1:
                DelFirst(hb, &qb);
                InsFirst(ha, qb);
                qb = NextPos(*Pb, hb);
                ha = NextPos(*Pa, ha);
                break;
        }
    }

    if (!ListEmpty(*Pb)) {
        Append(*Pa, qb);
    }

    FreeNode(hb);
}

// 打印多项式函数
void PrintPolynomial(Polynomial P) {
    Polynomial p = P->next;
    while (p) {
        printf("%dx^%d", p->coef, p->expo);
        if (p->next) {
            printf(" + ");
        }
        p = p->next;
    }
    printf("\n");
}

// 创建多项式函数
Polynomial CreatePolynomial() {
    Polynomial head = (Polynomial)malloc(sizeof(PolyNode));
    head->next = NULL;
    return head;
}

// 向多项式中添加项函数
void AddTerm(Polynomial P, int coef, int expo) {
    Polynomial newNode = (Polynomial)malloc(sizeof(PolyNode));
    newNode->coef = coef;
    newNode->expo = expo;
    newNode->next = NULL;

    Polynomial p = P;
    while (p->next && p->next->expo > expo) {
        p = p->next;
    }

    if (p->next && p->next->expo == expo) {
        p->next->coef += coef;
        if (p->next->coef == 0) {
            Polynomial temp = p->next;
            p->next = p->next->next;
            free(temp);
        }
    } else {
        newNode->next = p->next;
        p->next = newNode;
    }
}

int main() {
    Polynomial Pa = CreatePolynomial();
    Polynomial Pb = CreatePolynomial();

    // 向多项式 Pa 中添加项
    AddTerm(Pa, 3, 2);
    AddTerm(Pa, 2, 1);
    AddTerm(Pa, 1, 0);

    // 向多项式 Pb 中添加项
    AddTerm(Pb, 4, 2);
    AddTerm(Pb, 3, 1);
    AddTerm(Pb, 2, 0);

    printf("多项式 Pa: ");
    PrintPolynomial(Pa);

    printf("多项式 Pb: ");
    PrintPolynomial(Pb);

    AddPolyn(&Pa, &Pb);

    printf("多项式 Pa + Pb: ");
    PrintPolynomial(Pa);

    // 释放内存
    Polynomial temp;
    while (Pa) {
        temp = Pa;
        Pa = Pa->next;
        free(temp);
    }
    while (Pb) {
        temp = Pb;
        Pb = Pb->next;
        free(temp);
    }

    return 0;
}

算法2.23

#include <stdio.h>
#include <stdlib.h>

// 多项式项的结构体
typedef struct PolyNode {
    int coef;  // 系数
    int expo;  // 指数
    struct PolyNode *next;
} PolyNode, *Polynomial;

// 创建新的多项式项节点
PolyNode *createNode(int coef, int expo) {
    PolyNode *newNode = (PolyNode *)malloc(sizeof(PolyNode));
    if (newNode == NULL) {
        printf("内存分配失败\n");
        return NULL;
    }
    newNode->coef = coef;
    newNode->expo = expo;
    newNode->next = NULL;
    return newNode;
}

// 插入多项式项到链表中（按照指数降序排列）
void insertTerm(Polynomial *poly, int coef, int expo) {
    PolyNode *newNode = createNode(coef, expo);
    if (*poly == NULL) {
        // 如果链表为空，直接将新节点作为链表的头节点
        *poly = newNode;
    } else {
        PolyNode *curr = *poly;
        PolyNode *prev = NULL;
        while (curr!= NULL && curr->expo > expo) {
            prev = curr;
            curr = curr->next;
        }
        if (curr!= NULL && curr->expo == expo) {
            // 如果指数相同，系数相加
            curr->coef += coef;
            free(newNode);
            if (curr->coef == 0) {
                // 如果相加后系数为 0，删除该节点
                if (prev == NULL) {
                    *poly = curr->next;
                } else {
                    prev->next = curr->next;
                }
                free(curr);
            }
        } else {
            // 插入新节点
            if (prev == NULL) {
                newNode->next = *poly;
                *poly = newNode;
            } else {
                newNode->next = curr;
                prev->next = newNode;
            }
        }
    }
}

// 多项式相加函数
Polynomial addPolynomials(Polynomial poly1, Polynomial poly2) {
    Polynomial result = NULL;
    PolyNode *p1 = poly1;
    PolyNode *p2 = poly2;

    while (p1!= NULL && p2!= NULL) {
        if (p1->expo > p2->expo) {
            insertTerm(&result, p1->coef, p1->expo);
            p1 = p1->next;
        } else if (p1->expo < p2->expo) {
            insertTerm(&result, p2->coef, p2->expo);
            p2 = p2->next;
        } else {
            int coefSum = p1->coef + p2->coef;
            insertTerm(&result, coefSum, p1->expo);
            p1 = p1->next;
            p2 = p2->next;
        }
    }

    while (p1!= NULL) {
        insertTerm(&result, p1->coef, p1->expo);
        p1 = p1->next;
    }

    while (p2!= NULL) {
        insertTerm(&result, p2->coef, p2->expo);
        p2 = p2->next;
    }

    return result;
}

// 多项式相乘函数
Polynomial multiplyPolynomials(Polynomial poly1, Polynomial poly2) {
    Polynomial result = NULL;
    PolyNode *p2 = poly2;

    while (p2!= NULL) {
        Polynomial temp = NULL;
        PolyNode *p1 = poly1;
        while (p1!= NULL) {
            int coef = p1->coef * p2->coef;
            int expo = p1->expo + p2->expo;
            insertTerm(&temp, coef, expo);
            p1 = p1->next;
        }
        result = addPolynomials(result, temp);
        p2 = p2->next;
    }

    return result;
}

// 打印多项式
void printPolynomial(Polynomial poly) {
    PolyNode *curr = poly;
    while (curr!= NULL) {
        printf("%dx^%d", curr->coef, curr->expo);
        curr = curr->next;
        if (curr!= NULL) {
            printf(" + ");
        }
    }
    printf("\n");
}

// 释放多项式链表的内存
void freePolynomial(Polynomial poly) {
    PolyNode *curr = poly;
    PolyNode *next;

    while (curr!= NULL) {
        next = curr->next;
        free(curr);
        curr = next;
    }
}

int main() {
    Polynomial poly1 = NULL;
    Polynomial poly2 = NULL;

    // 构建第一个多项式：3x^2 + 2x + 1
    insertTerm(&poly1, 3, 2);
    insertTerm(&poly1, 2, 1);
    insertTerm(&poly1, 1, 0);

    // 构建第二个多项式：2x^2 - 1
    insertTerm(&poly2, 2, 2);
    insertTerm(&poly2, -1, 0);

    printf("多项式 1: ");
    printPolynomial(poly1);

    printf("多项式 2: ");
    printPolynomial(poly2);

    Polynomial product = multiplyPolynomials(poly1, poly2);

    printf("相乘后的结果: ");
    printPolynomial(product);

    // 释放内存
    freePolynomial(poly1);
    freePolynomial(poly2);
    freePolynomial(product);

    return 0;
}

总结

1.1. 线性表的概念

线性表是n个相同类型数据元素的有限序列（n≥0）。
具有如下特征：

- 存在一个唯一的“第一个”数据元素。
- 存在一个唯一的“最后一个”数据元素。
- 除第一个之外，每个数据元素均有且仅有一个前驱。
- 除最后一个之外，每个数据元素均有且仅有一个后继。

1.2. 线性表的分类

线性表的抽象数据类型（ADT）：定义了线性表的基本操作集。
顺序表：线性表的顺序存储结构，利用一组地址连续的存储单元依次存放线性表中的各个元素。
链表：线性表的链式存储结构，通过一组任意的存储单元来存储线性表中的数据元素，每个存储单元（节点）包括数据域和指针域。

1.3. 顺序表的特点

随机存取：可以直接通过计算得到任一元素的地址。
插入和删除操作需要移动元素，效率较低。
需要预分配足够的存储空间。

1.4. 链表的特点

动态存储分配：不需要预分配存储空间，可以动态申请和释放节点。
插入和删除操作效率高，仅需修改指针。
随机访问效率低，需要从头节点开始遍历。

1.5. 链表的类型

单链表：每个节点仅包含一个指向其后继节点的指针。
双链表：每个节点包含两个指针，分别指向其前驱和后继节点。
循环链表：最后一个节点的指针指向头节点，形成环状结构。
静态链表：使用静态数组实现的链表，利用数组下标作为指针。

1.6. 线性表的操作

初始化：创建一个空的线性表。
插入：在表中插入一个元素。
删除：从表中删除一个元素。
查找：在表中查找一个元素。
遍历：访问表中的所有元素。
求长度：获取表中元素的数量。

1.7. 时间复杂度分析

顺序表中，插入和删除操作的时间复杂度为O(n)，查找和求长度操作的时间复杂度为O(1)。
链表中，插入和删除操作的时间复杂度为O(1)（在已知前驱节点的情况下），查找操作的时间复杂度为O(n)。

1.8. 空间复杂度分析

顺序表的空间复杂度为O(n)。
链表的空间复杂度也为O(n)，但额外需要存储指针。

通过理解和掌握这些概念和操作，你可以有效地使用线性表解决实际问题，同时为学习更复杂的数据结构奠定坚实的基础。

拓展的学习内容

线性表

将两个或两个以上的线性表合并成一个线性表；
把一个线性表拆开成两个或两个以上的线性表；
重新复制一个线性表等;