目标物体的轮廓提取
- 轮廓提取法
- 边界跟踪法
- 区域增长法
- 区域分裂合并法
一、轮廓提取法
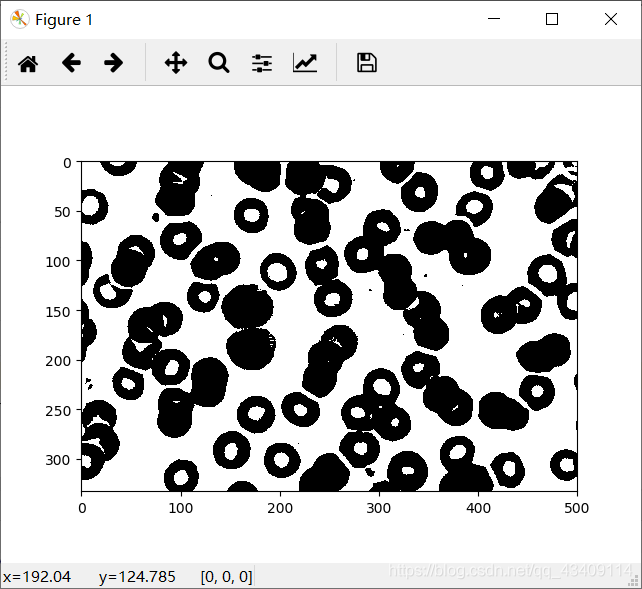
对于二值图像的轮廓提取,我们可以采用掏空内部点法,如果原图中有一点为黑,且它的8个相邻的点都为黑,则将该点删除。对于非二值图像,要先进行二值处理
掏空内部点法实现如下
def GetOutLine(self):
img=np.copy(self.Img)
for y in range(1,len(self.Img)):
for x in range(1,len(self.Img[y])):
if self.Img[y,x,0]!=0:
continue
sum=np.sum(self.Img[y-1:y+2,x-1:x+2,0])
if sum==0:
img[y,x]=np.array([255,255,255])
self.Img=img
原二值图像如下
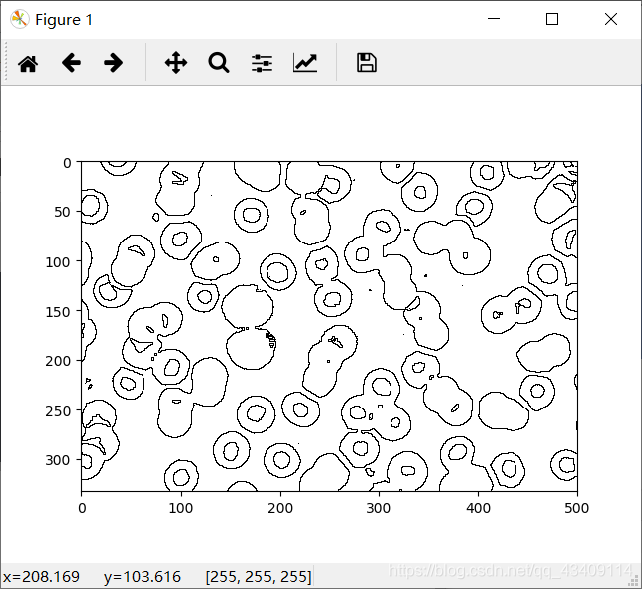
效果图如下
二、边界跟踪法
从图像的某个边界点出发,然后按照某种策略,搜索下一个边界点。直到搜索点与初始点重合,即找到轮廓。
def GetOutLine2(self):
img=np.empty(shape=[len(self.Img),len(self.Img[0]),3],dtype=int)
isok=np.zeros(shape=[len(self.Img),len(self.Img[0])])
img[:,:,:]=255
def getDirection(x,y,d):
operater=[[1,1],[0,1],[-1,1],[-1,0],[-1,-1],[0,-1],[1,-1],[1,0]]
return x+operater[d][0],y+operater[d][1]
# 下面两个for循环则是用来扫描图像的
for y in range(1,len(self.Img)):
for x in range(1,len(self.Img[y])):
#判断点是否已经被跟踪
if img[y][x][0]==0:
continue; #如果被跟踪,则跳过该点
if self.Img[y][x][0]==255:
continue; #如果该点是白像素,则也跳过。其上两则可以合并,只是这样写,更好看
direction=0
init_x,init_y=x,y
last_x,last_y=x,y
min_x,min_y,max_x,max_y=x,y,x,y
while True:
# 得到等待搜索的目标
c=0
while c<=8:
new_x,new_y=getDirection(last_x,last_y,direction)
c=c+1
#判断得出的坐标是否再范围之内
if new_x<0 or new_x>len(self.Img[0])-1 or new_y<0 or new_y>len(self.Img)-1:
direction = (direction + 1) % 8
continue
#然后判断该目标是否符合条件
if self.Img[new_y][new_x][0]==0 and img[new_y][new_x][0]==255 and isok[new_y][new_x]==0:
'如果符合条件,则'
img[new_y][new_x][:] =0 # 置缓存图像中对应的像素点的像素值为黑色
last_x,last_y=new_x,new_y #更新坐标点
direction = (direction - 2) % 8
if direction<0: #有可能是负值,将其置正
direction=direction+8
#下面代码是用来求已标记区域的
min_x=min(min_x,new_x)
min_y=min(min_y,new_y)
max_x=max(max_x,new_x)
max_y=max(max_y,new_y)
break
else:
direction=(direction+1)%8
if c==9: #如果是孤立黑色像素,则跳过
break
if new_x==init_x and new_y==init_y: #如果回到初始坐标则跳出
isok[min_y:max_y+1,min_x:max_x+1]=1
break
self.Img=img
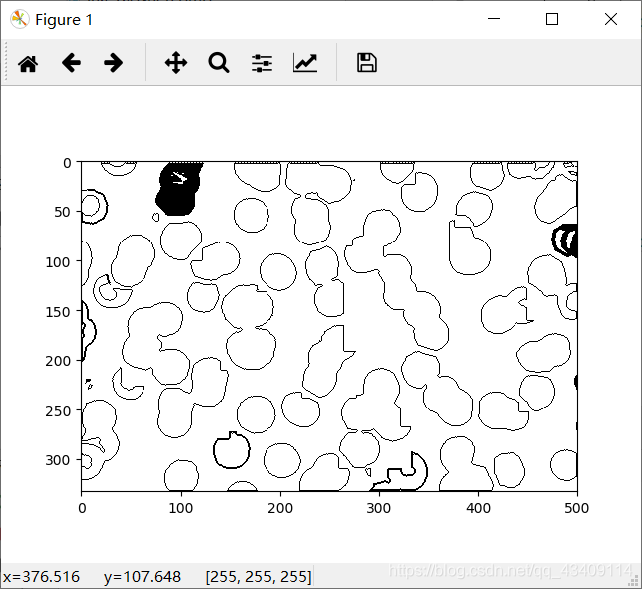
效果图如下
三、区域增长法
依次用图像的每一个像素的灰度值和种子点相减,判断结果是否小于标准差,如果小于则将该点和种子点合并,不是则保持像素点的灰度值不变。这样处理后的图像就用区域分割法处理后的边缘分割图像
三个要点
- 选择合适的种子点
- 确定相似性条件
- 确定停止生长的条件
def GetOutLine3(self,star_x,star_y):
thread=10 #阈值
stack=[] #建立一个空栈,用来广度优先遍历
#下面遍历这个初始为止的八领域
c_x,c_y=star_x,star_y
direction=[[1,1],[0,1],[-1,1],[-1,0],[-1,-1],[0,-1],[1,-1],[1,0]]
isok=np.empty(shape=[len(self.Img),len(self.Img[0])],dtype=bool)
img=np.empty(shape=[len(self.Img),len(self.Img[0]),3],dtype=int)
while True:
for d in direction:
x0=c_x+d[0]
y0=c_y+d[1]
if x0<0 or x0>=self.f_width or y0<0 or y0>=self.f_height:
continue
if self.Img[y0][x0][0]-self.Img[c_y][c_x][0]<thread and isok[y0,x0]==False:
stack.append((x0,y0))
isok[y0,x0]=True
if len(stack)==0:
break
c_x,c_y=stack.pop(-1)
self.Img=img
四、区域分裂合并法
利用金字塔或者四叉树数据结构的层次概念,将图像划分成一组任意不相交的初始区域,即从金字塔或者四叉树结构的任意中间层开始,根据给定的均匀性检测准则进行分裂和合并这些区域。逐步改善区域划分性能,直到最后将图像分成数量最少的均匀区域为之
如何确定区域的相似性呢?
基于区域的灰度值,或者基于区域边界的强弱项。简单的方法就下比较他们的灰度均值
关于代码的实现其实也不难。完完全全可以参照归并排序的代码实现,利用递归,可以很简短的实现该算法。