KMP算法之next数组详解
KMP算法实现原理
KMP算法是一种非常高效的字符串匹配算法,下面我们来讲解一下KMP算如何高效的实现字符串匹配。我们假设如下主串和模式串:
int i;//i表示主串的下标
int j;//j表示模式串的下标
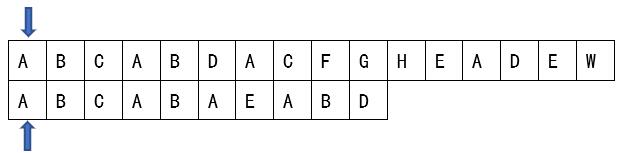
char P[]=“ABCABDACFGHEADEW”;//主串
char T[]=“ABCABAEABD”;//模式串
开始查找
while (i<strlen(P) && j<strlen(T))
{
if (P[i] == T[j])//字符匹配上就移动到下一个,继续匹配
{
i++;
j++;
}
else
{
i = i - j + 1;
j = 0;
}
}
if (j == strlen(T))//说明此时匹配成功
{
return i-j;
}
else
{
return -1;
}
上述字符创匹配方式非常容易理解,其实现原理就是一个字符一个字符进行匹配,这就是BF算法。但是,显然上述字符串匹配方式的效率太低,因为他只要匹配失败就从头开始匹配。然而,在大多数情况下我们都是不需要进行重复匹配的。
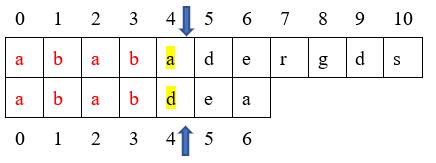
举个栗子:主串:ababadergds 模式串:ababdea
我们可以看出在进行第一次匹配时,前面已经有四个字符{a,b,a,b}匹配成功,在进行第五个字符的匹配时,匹配失败。按照BF算法则需要重新回退回去再次进行匹配,但是那种方法效率太低,那么我们能不能利用上次匹配的结果进行优化呢?
答案是肯定的!下面我们就开始介绍著名的KMP算法!!!
介绍KMP算法之前,我们先简单介绍一下KMP算法的思想。首先,KMP算法的思想之一就是只让模式串回退,主串的下标只增不减。思想之二就是模式串回退时会利用子串的最大相同前缀、后缀(后面介绍最大相同前缀、后缀)。
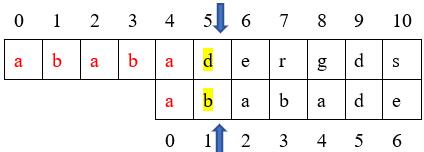
好了,我们接着上一次匹配往下看,通过观察,我们知道第一次匹配时,子串abab是匹配成功的,这说明主串和模式串中都含有字符abab这个子串(稍后会介绍什么是子串)。另外,在子串中我们可以看出abab这个子串的前两个字符和后两个字符都是ab,是相同的。那么我们就可以思考,在将模式串回退时,我们是不是可以将模式串回退到模式串下标为2的这个位置然后再进行匹配?
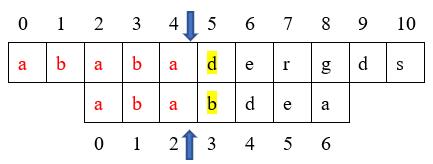
通过上面图,我们又可以看出,主串中的aba与模式串中的aba又是匹配的,而且在匹配的子串aba中前缀a与后缀a也是相同的。因此,在进行下一次的匹配过程中,我们将模式串移动到模式串下标1对应的位置,而不是从零开始。
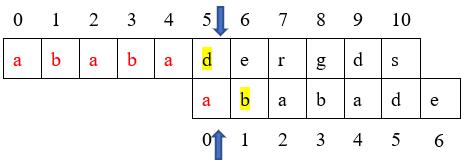
上面介绍的就是KMP算法的实现原理,即利用相同最长前缀、后缀来移动模式串。另外,在我们进行移动时,细心的朋友可以发现我们在移动模式串时,总是通过已经匹配成功的子串,然后看子串中的最大相同前缀、后缀来移动模式串。而这个匹配成功的子串本身就是模式串中的子串,并不受主串的影响。因此,我们完全可以只通过模式串来查看子串,最后确定要移动的位数,这个要移动的位数我们把它定义成一个数组,这个数组就称之为next数组。
讲next数组之前,我们补充一下什么是子串
对于字符串:abddfsag
它所拥有的前缀子串为{a,ab,abd,abdd,abddf,abddfs,abddfsa}
它所拥有的后缀子串为{g,ag,sag,fsag,dfsag,ddfsag,bddfsag}
即前缀子串不能包含最后一个字符,后缀子串不能包含第一个字符(和数学里集合中的真子集有点像哈,即一个字符串的子串只能是其真子集)
剖析NEXT数组
最大相同前缀、后缀是相对于子串来讲的,即每一个子串都有一个最大相同前缀。例如,对于字符串:“ababce”,j表示字符串位置的下标。
当j=0时,对应字符a位置,a前面没有字符,故此时不存在前缀,后缀(看前缀、后缀时,j所在的位置不算,只看其前面的字符),此时令next[0]=-1;。
当j=1时,只有字符a,一个字符不存在前缀、后缀,有next[1]=0;。
当j=2时,此时j前面的子串为ab,由于a和b不相等,故最大相同前后缀为零,next[2]=0。
当j=3时,此时j前面的子串为aba,aba的前缀子串{a,ab},后缀子串{a,ba},因此其最大相同前后缀为1,next[3]=1。
当j=4时,此时j前面的子串abab,abab的前缀子串{a,ab,aba},后缀子串{b,ab,bab},故最大相同前后缀为ab,next[4]=2。
当j=5时,此时j前面的子串ababc,ababc的前缀子串{a,ab,aba,abab},后缀子串{c,bc,abc,babc},故最大相同前后缀为0,next[5]=0。
通过最大相同前后缀我们就可以求出next数组。
现在我们可能有个疑问,费劲求出next数组,那么next数组有什么用呢?
next数组非常有用!!!它就是我们实现KMP算法的关键!!!
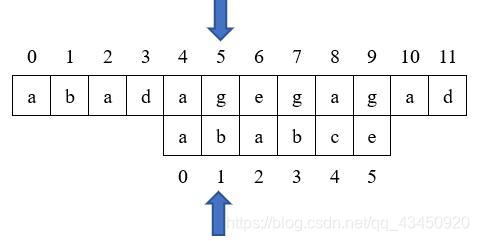
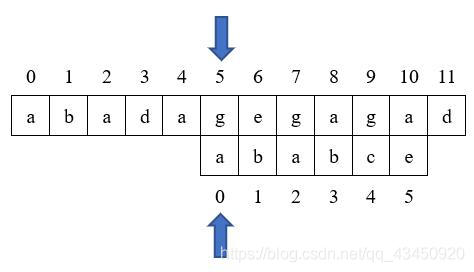
例如我们要在主串:“abadagegahad"中查找模式串"ababce”,查找步骤如下:
1.
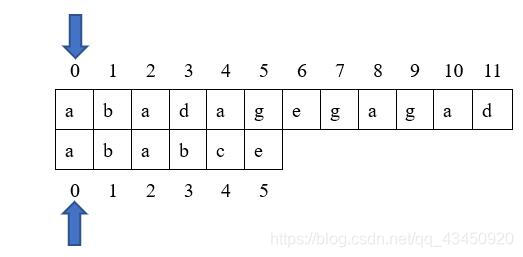
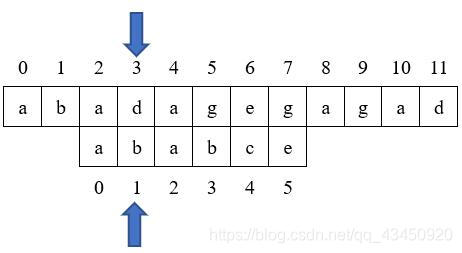
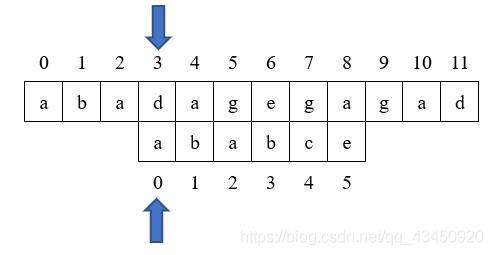
下面直接将匹配的图示列出
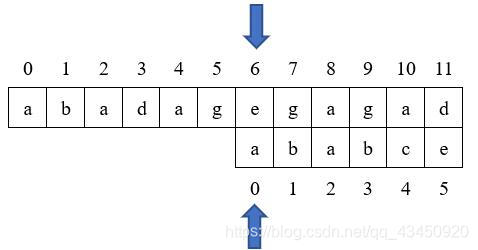
那么,既然我们知道了KMP算法的实现原理和如何移动模式串,那么我们获得一个next数组的代码该怎么写呢?
下面先把代码附下面:
int *GetNext(char *pStr, int n)
{
int j;
int k = 0;
int next[10] = {0};
next[0] = -1;
for (j = 1; j < n-1; j++)//j表示子串的长度
{
if (pStr[k] == pStr[j])
{
next[j+1] = k + 1;
k++;
}
else
{
j = j - k ;
//只要有一次失败匹配失败,则说明当前子串不匹配,需要对子串的长度减一,进行下一次匹配
k = 0;
}
}
return next;
}
上面代码中else语句中的k=0是什么意思呢?
首先我们假设我们在进行当前判断之前,已经有k个最大前后缀,如果T[k]==T[j],则说明这个字符也匹配成功,那么就令next[j+1]=k+1;如果匹配失败,则字符子串的长度减一,然后将k置为零来重新计算next数组,k置为零的目的是为了重新从开头计算next数组,此时j应该为j=j-k+1,由于for循环里有了j++,故else语句里另j=j-k。通过这个循环,便可求得next数组。
不过,让我们再思考一下,else里的k=0还可以继续优化吗?
答案是肯定的!优化后的代码如下:
int *GetNext(char *pStr, int n)
{
int i;
int j;
int k = 0;
int next[10] = {0};
next[0] = -1;
for (j = 1; j < n-1; j++)//j表示子串的长度
{
if (pStr[k] == pStr[j])
{
next[j+1] = k + 1;
k++;
}
else
{
j = j - k ;
//只要有一次失败匹配失败,则说明当前子串不匹配,需要对子串的长度减一,进行下一次匹配
if (k != 0)
{
k = next[k];//这是什么意思呢?
}
}
}
return next;
}
上述优化其实只是做了k=next[k];的赋值,然而很多人就卡在这一个赋值上,为什么要这样赋值呢?
答案其实很简单,因为我们要想查找最大前后缀,在每次匹配之后都要重新“从头”开始查找,然而,当我们前面已经匹配成功k个字符时,第k+1个字符匹配失败了,那么我们需要将模式串从头开始重新匹配,但是如果我们细心点我们可以发现,前面k个字符同样包含最大前后缀,因此令k=next[k]实质上就是将模式串回溯到前面k个字符所拥有的最大前后缀的位置上(但是你要是令k=0也不会出错,只是效率稍微降低),如果前面k个字符中最大前后缀为零,另k=next[k]与k=0实际上是一个效果。
好了,这就是KMP算法的实现原理,文中有讲的不清楚或者不对的地方,欢迎大家批评指正!!!
如果有什么问题也欢迎大家在评论区留言!!!