目录
1.3.5 补充(决策边界不是训练集的属性,而是假设本身及其参数的属性 解释这句话)
1. 逻辑回归(分类问题中的算法)
1.1 分类问题
1.1.1 定义与示例
①任务目标
预测离散类别标签 y∈{0,1},其中:y=0 表示负向类(如良性肿瘤、正常邮件),y=1 表示正向类(如恶性肿瘤、垃圾邮件)。
②典型场景
- 垃圾邮件检测(是/否)。
- 金融欺诈识别(正常交易/欺诈交易)。
1.1.2 线性回归的局限性
线性回归的假设函数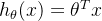
1.2 逻辑回归的核心思想
1.2.1 逻辑回归的定义
- 本质:一种分类算法,输出值严格限制在 [0, 1]区间,表示样本属于正向类的概率。
- 关键改进:通过 Sigmoid 函数(逻辑函数)将线性组合
映射到概率区间。
1.2.2 逻辑回归的假设函数
- 定义:
:线性组合(如
)。
- g(z):Sigmoid 函数(逻辑函数),将线性结果映射到 [0,1] 区间。
1.2.3 Sigmoid 函数
-
公式:
- 输入:线性组合
- 输出:
,表示
。
- 输入:线性组合
1.2.4 逻辑回归的假设函数
- 概率解释:
- 表示在给定输入 x 和参数
时,y=1 的概率。
- 示例:若
,则有 70% 的概率属于正向类(如恶性肿瘤),30% 属于负向类。
- 表示在给定输入 x 和参数
1.3 判定边界
1.3.1 判定边界的定义
- 核心概念:判定边界是模型将数据分为不同类别的分界线。
- 数学表达:在逻辑回归中,判定边界由方程
定义。
- 当
时,预测 y=1。
- 当
时,预测 y=0。
- 当
1.3.2 线性判定边界
- 示例模型:
- 参数
。
- 假设函数:
。
- 参数
- 判定边界方程:
- 几何解释:在二维平面上,这是一条直线,将区域分为两部分:
时预测 y=1 。
时预测 y=0 。
- 几何解释:在二维平面上,这是一条直线,将区域分为两部分:
1.3.3 非线性判定边界
- 问题场景:当数据无法用直线分隔时(如环形分布),需引入多项式特征。
- 示例模型:
- 参数
。
- 假设函数:
。
- 参数
- 判定边界方程:
- 几何解释:这是一个以原点为中心、半径为1的圆,圆内预测 y=0,圆外预测 y=1。
1.3.4 判定边界的灵活性
- 高阶特征的作用:通过添加高次项(如
),可构造复杂的判定边界(如椭圆、抛物线)。
- 示例:
- 若假设函数为
,可拟合圆形或椭圆形边界。
- 若假设函数为
1.3.5 补充(决策边界不是训练集的属性,而是假设本身及其参数的属性 解释这句话)
①核心概念拆解
- 决策边界(Decision Boundary):模型用来区分不同类别的分界线(如直线、曲线)。
- 训练集(Training Set):用于训练模型的数据集合。
- 假设(Hypothesis):模型的数学形式(如逻辑回归的
)。
- 参数(Parameters):模型中的可调整变量(如
)。
② 为什么决策边界属于假设和参数?
(1) 决策边界的数学定义
- 在逻辑回归中,决策边界由方程
定义。
- 示例:若
,则决策边界为
。
- 示例:若
- 关键点:边界的形式直接由参数
和模型假设(是否包含多项式项)决定。
(2) 训练集的作用
- 训练集仅影响参数值:通过训练数据调整
,使模型更好地拟合数据。
- 不改变边界形式:无论数据如何分布,决策边界的形状(如直线、圆)由模型假设预先确定。
③训练集 vs 假设与参数
| 维度 | 训练集 | 假设与参数 |
|---|---|---|
| 影响内容 | 决定参数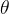 的具体数值 的具体数值 | 决定决策边界的形状(直线、圆等) |
| 可变性 | 不同训练集 → 不同 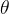 | 固定假设 → 边界形式固定 |
| 示例 | 数据分布影响直线的位置 | 是否添加 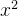 项决定边界是直线还是圆 项决定边界是直线还是圆 |
④ 总结
- 决策边界的形状由模型假设(如是否包含多项式项)和参数
共同决定。
- 训练集的作用:仅通过调整参数
来优化边界的位置或大小,但无法改变边界的固有形式。
类比:
- 假设和参数 → 模具的形状(如圆形、方形)。
- 训练集 → 调整模具的大小和位置,但无法改变其基本形状。
1.4 代价函数
1.4.1 逻辑回归代价函数的必要性
- 问题:直接使用线性回归的平方误差代价函数会导致非凸优化(存在多个局部最小值),难以找到全局最优解。
- 核心改进:定义新的代价函数,使其为凸函数(单峰,无局部最优)。
1.4.2 代价函数定义
- 单个样本的代价(y = 0 or 1 always !):
- 统一公式:
- 整体代价函数(所有训练样本的平均):
1.4.3 直观理解
- 当 y=1 时:
- 若预测
,代价
。(预测对了是应该的,没有奖励)
- 若预测
,代价
(预测错了加大惩罚力度)。
- 若预测
- 当 y=0 时:
- 若预测
,代价
。
- 若预测
,代价
。
- 若预测
1.4.4 Python 代码实现
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost(theta, X, y):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
h = sigmoid(X * theta.T)
term1 = np.multiply(-y, np.log(h))
term2 = np.multiply((1 - y), np.log(1 - h))
return np.sum(term1 - term2) / len(X)
1.5 梯度下降
1.5.1 梯度下降算法
- 目标:最小化
,找到最优参数
。
- 参数更新规则:
1.5.2 与线性回归对比
| 维度 | 线性回归 | 逻辑回归 |
|---|---|---|
| 假设函数 | 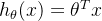 |  |
| 代价函数 | 均方误差(MSE) | 交叉熵损失(Cross-Entropy Loss) |
| 梯度公式 | 形式上相同,但假设函数不同 | 形式上相同,但假设函数不同 |
- 核心区别:
虽然梯度更新公式在数学形式上一致,但由于逻辑回归的假设函数引入了 Sigmoid 函数,实际计算中梯度方向不同。
1.5.3 实现步骤
- 初始化参数:
- 设置
初始值(通常为全零向量)。
- 设置
- 计算假设函数:
- 计算代价函数:
- 计算梯度并更新参数:
- 重复迭代:直到代价函数收敛(最小化代价函数)或达到最大迭代次数。
1.5.4 关键注意事项
- 特征缩放:
- 若特征范围差异大(如
,
),需进行标准化(如 Z-Score 归一化),加速梯度下降收敛。
- 若特征范围差异大(如
- 学习率选择:
- 过大:可能跳过最优解;过小:收敛速度慢。建议尝试
等。
- 过大:可能跳过最优解;过小:收敛速度慢。建议尝试
- 监控收敛:
- 绘制代价函数随迭代次数的变化曲线,确保其单调下降。
1.5.5 类比
- 代价函数像“纠错老师”:预测越错,惩罚越大,推动模型快速修正参数。
- 梯度下降像“下山”:每一步根据坡度(梯度)调整方向,逻辑回归的“山形”由 Sigmoid 函数塑造,与线性回归的“平缓山坡”不同
- 收敛速度通常快于梯度下降。
1.5.6 代码示例
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def compute_cost(theta, X, y):
m = len(y)
h = sigmoid(X.dot(theta))
cost = (-y.dot(np.log(h)) - (1 - y).dot(np.log(1 - h))) / m
return cost
def gradient_descent(X, y, theta, alpha, num_iters):
m = len(y)
cost_history = []
for _ in range(num_iters):
h = sigmoid(X.dot(theta))
gradient = (X.T.dot(h - y)) / m
theta -= alpha * gradient
cost_history.append(compute_cost(theta, X, y))
return theta, cost_history
1.6 高级优化
1.6.1 为什么需要高级优化?
- 梯度下降的局限性:
- 需手动调整学习率
,选择不当会导致收敛慢或震荡。
- 高维特征或大数据集时,计算效率低(如百万样本+千维特征)。
- 需手动调整学习率
- 高级优化的优势:
- 自动学习率:内置智能搜索(如线性搜索),动态调整步长。
- 更快收敛:利用二阶导数信息(如曲率),减少迭代次数(从千次降至几十次)。
1.6.2 高级优化算法原理
①共轭梯度法(Conjugate Gradient)
- 核心思想:迭代过程中选择共轭方向(相互正交的方向),避免重复搜索。
- 优点:内存占用低,适合中等规模问题。
② BFGS(变尺度法)
- 核心思想:通过近似Hessian矩阵(二阶导数矩阵)更新参数,加速收敛。
- 优点:比梯度下降更快收敛,但需存储Hessian矩阵的近似值,内存消耗较高。
③L-BFGS(限制变尺度法)
- 核心思想:BFGS的改进版,仅保存最近几步的更新信息,减少内存占用。
- 优点:适合大规模数据(如特征维度超过1万)。
1.6.3 使用步骤详解
①编写代价函数与梯度计算代码
- 代价函数:计算
。
- 梯度计算:计算
。
Python代码示例:
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def compute_cost_and_gradient(theta, X, y):
# 将theta转换为列向量(适配numpy矩阵运算)
theta = theta.reshape(-1, 1)
m = len(y)
# 计算假设函数h_theta(x)
h = sigmoid(X.dot(theta))
# 计算代价函数J(theta)
cost = (-y.T.dot(np.log(h)) - (1 - y).T.dot(np.log(1 - h))) / m
# 计算梯度
gradient = (X.T.dot(h - y)) / m
# 将梯度展平为一维数组(适配优化库输入)
gradient = gradient.flatten()
return cost, gradient
②调用优化库函数
使用SciPy的minimize函数:
from scipy.optimize import minimize
# 输入数据:X为特征矩阵(m×n),y为标签向量(m×1)
initial_theta = np.zeros(X.shape[1]) # 初始参数(全零向量)
# 调用L-BFGS算法优化
result = minimize(
fun=compute_cost_and_gradient, # 目标函数(返回代价和梯度)
x0=initial_theta, # 初始参数
args=(X, y), # 额外参数(传递给fun)
method='L-BFGS-B', # 使用L-BFGS算法
jac=True # fun同时返回梯度
)
# 提取最优参数
opt_theta = result.x
1.6.4 关键注意事项
①特征缩放
- 即使使用高级算法,仍需对特征标准化(如Z-Score归一化),否则收敛速度可能受影响。
- 示例:若特征
,
,归一化后
②代码细节
- 参数形状:
theta需转换为列向量以适配矩阵乘法,梯度需展平为一维数组以适配优化库。 - 返回值:代价函数返回标量值,梯度返回一维数组。
③算法选择
- 小规模数据:BFGS或共轭梯度法。
- 大规模数据:优先L-BFGS。
1.6.5 直观理解:梯度下降 vs 高级优化
- 梯度下降:像“盲人下山”,每一步试探坡度(梯度),手动调整步长(学习率)。
- 高级优化:像“自动驾驶汽车”,自动探测地形曲率(二阶导数),动态调整方向和步长。
示例:
- 任务:拟合逻辑回归模型(10,000个特征,100,000个样本)。
- 梯度下降:需手动调参,迭代10,000次,耗时数小时。
- L-BFGS:自动调参,迭代100次,耗时几分钟。
1.7 多类别分类:一对多
1.7.1 多类别分类问题概述
- 定义:预测离散类别标签
,其中 K 为类别总数(
)。
- 示例:
- 邮件分类:工作(y=1)、朋友(y=2)、家人(y=3)、兴趣(y=4)。
- 疾病诊断:健康(y=1)、感冒(y=2)、流感(y=3)。
- 天气预测:晴天(y=1)、多云(y=2)、雨天(y=3)、雪天(y=4)。
1.7.2 一对多方法的核心思想
- 核心策略:将多类别分类问题转化为多个二元分类问题。
- 具体步骤:
- 对每个类别 i(
):
- 将类别 i 标记为正类(y=1)。
- 其余所有类别标记为负类(y=0)。
- 训练 K 个二元分类器:每个分类器
学习区分类别 i 与其他类别。
- 对每个类别 i(
1.7.3 实现步骤
-
构建伪训练集:
- 示例:训练分类器
时,将类别1的样本标记为1,其他类别标记为0。
- 重复:对每个类别 i,构建对应的训练集并训练分类器。
- 示例:训练分类器
-
训练分类器:
- 模型假设:
- 目标:分类器
输出样本属于类别 i 的概率。
- 模型假设:
1.7.4 预测方法
- 预测规则:对于新样本 x,选择所有分类器中概率最高的类别:
- 示例:
- 若
,
,
,则预测 y=1。
- 若
1.7.5 注意事项与总结
- 标签索引无关性:类别标签可从0或1开始编号,不影响算法逻辑。
- 适用性:
- 适用于类别数 K 较大的场景(如10个类别)。
- 每个分类器独立训练,可并行化加速。
- 潜在问题:
- 类别不平衡:若某类别样本数远多于其他类别,分类器可能偏向多数类。
- 计算成本:需训练 K 个分类器,时间和资源消耗随 K 增加而增长。
1.7.6 总结
- 一对多方法:通过多次二元分类解决多类别问题,简单有效。
- 核心公式:
(第 i 个分类器)
- 预测准则:
类比:一对多方法像“轮流考试”:每个分类器只回答“是否属于某个特定类别”,最终选择得分最 高的答案。
2. 正则化(Regularization)
2.1 过拟合问题
2.1.1 过拟合的定义与示例
- 定义:模型在训练集上表现极好(如代价函数接近零),但在新数据上泛化能力差。
- 根本原因:模型复杂度过高,过度拟合训练数据中的噪声或细节。
2.1.2 过拟合的直观表现
-
回归问题示例:
- 欠拟合(高偏差):模型过于简单(如线性模型),无法捕捉数据趋势。例如,用直线拟合抛物线分布的数据,预测误差较大。
- 适度拟合:模型复杂度适中(如二次多项式),既能拟合数据趋势,又保持对新数据的预测能力。
- 过拟合(高方差):模型过于复杂(如四次多项式),完美拟合训练数据但无法预测新样本。例如,高阶多项式曲线穿过所有训练点,但对新输入的预测可能剧烈波动。
-
分类问题示例:
- 欠拟合:决策边界过于简单(如直线),无法区分类别。例如,用直线分隔明显呈圆形分布的两类数据。
- 过拟合:决策边界复杂(如高阶多项式),对训练数据中的噪声敏感。例如,分类边界扭曲以贴合个别异常点,导致新样本分类错误。
2.1.3 解决过拟合的方法
-
减少特征数量:
- 手动选择:手动选择保留关键特征,剔除冗余或噪声特征。例如,在房价预测中,仅保留面积和房间数,忽略无关特征。
- 自动选择:使用算法(如PCA、递归特征消除)筛选特征。
-
正则化(Regularization)(推荐):
- 核心思想:保留所有特征,但限制模型参数的大小,防止模型过度依赖某些特征。
2.2 正则化
2.2.1 正则化项的引入
- 线性回归的代价函数(未正则化)
- 正则化后的代价函数(L2正则化)

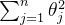

2.2.2 正则化的作用
- 抑制参数值:通过增大
,迫使参数
趋近于零,降低模型复杂度。
- 平衡偏差与方差:
过小:正则化效果弱,可能过拟合。
过大:模型过于简单,可能欠拟合。
2.2.3 正则化类型
- L2正则化(岭回归):
- 正则化项为
,倾向于让参数接近零但非零。
- 正则化项为
- L1正则化(Lasso回归):
- 正则化项为
,可产生稀疏参数(部分参数精确为零)。
- 正则化项为
2.2.4 正则化参数 的计算方法
的计算方法
正则化参数
①为什么  无法直接计算?
无法直接计算?
- 模型依赖性:
的合理取值与数据分布、特征数量、模型复杂度等因素密切相关。
- 目标平衡:
需要在偏差(欠拟合)和方差(过拟合)之间找到平衡,这需要通过实验验证。
②选择  的通用方法
的通用方法
(1) 交叉验证(Cross-Validation)
-
步骤:
- 将数据集分为训练集和验证集(或使用 K 折交叉验证)。
- 为
定义一个候选范围(如 0.001, 0.01, 0.1, 1, 10, 1002.)。
- 对每个
值训练模型,并计算验证集上的性能(如均方误差、准确率)。
- 选择验证集性能最佳的
。
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCV
# 定义候选 λ 值(注意:sklearn 中参数名为 alpha)
param_grid = {'alpha': [0.001, 0.01, 0.1, 1, 10, 100]}
# 使用网格搜索和交叉验证
ridge = Ridge()
grid_search = GridSearchCV(ridge, param_grid, cv=5)
grid_search.fit(X_train, y_train)
# 最佳 λ 值
best_lambda = grid_search.best_params_['alpha']
(2) 学习曲线分析
- 绘制训练集和验证集误差随
的变化曲线:
- 若验证误差随
增大先减小后增大,最佳
位于最低点。
- 若验证误差持续上升,说明模型可能始终欠拟合或过拟合,需调整候选范围。
- 若验证误差随
③调整  的实用技巧
的实用技巧
- 初始范围建议:
- 对数尺度尝试(如
)。
- 对于小数据集,从较小的
开始(如 0.01)。
- 对数尺度尝试(如
- 迭代优化:
- 先粗调(大范围搜索),再细调(小范围微调)。
- 观察模型在验证集上的表现,避免陷入局部最优。
④不同正则化类型的  选择
选择
- L1 正则化(Lasso):
越大,稀疏性越强(更多参数被压缩为零)。
- 适用于特征选择场景。
- L2 正则化(Ridge):
越大,参数整体缩小幅度越大。
- 适用于共线性较强的特征。
⑤示例:不同 的影响
的影响
 | 模型行为 | 训练集误差 | 验证集误差 |
|---|---|---|---|
| 0.001 | 接近无正则化,可能过拟合 | 低 | 高 |
| 0.1 | 适度正则化,平衡偏差与方差 | 中 | 最低 |
| 10 | 强正则化,模型简单,可能欠拟合 | 高 | 高 |
2.3 具体示例:正则化参数 如何抑制无关参数
如何抑制无关参数
我们通过一个简单的线性回归模型和手动计算,展示正则化如何抑制无关参数。
2.3.1 问题设定
- 数据集:3个样本,每个样本包含两个特征
(重要特征)和
(无关噪声)。
样本 y(真实值) 1 2 0.1 4 2 3 0.2 6 3 4 0.3 8 - 模型:
。
- 真实关系:
(与
无关)。
- 初始参数:
,
,
。
- 学习率:
,正则化参数
。
2.3.2 计算误差项与参数更新
步骤1:计算初始预测值
| 样本 | 预测值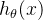 |
|---|---|
| 1 | |
| 2 | |
| 3 |
步骤2:计算误差项(对

- 误差项公式:
-
对
:
-
对
:
步骤3:参数更新(加入正则化)
- 更新公式:
,其中
,
。
-
更新
:
-
更新
:
2.3.3 分析参数变化
-
(重要参数):
- 误差项为 -9.0(绝对值大),推动
显著增大。
- 正则化轻微压缩(乘以 0.9967),但误差项主导,最终
从 1 → 1.8967。
- 误差项为 -9.0(绝对值大),推动
-
(无关参数):
- 误差项为 -0.62(绝对值小),正则化压缩效果更明显。
- 最终
从 1 → 1.0587,增长幅度远小于
。
2.3.4 多轮迭代后的结果
假设继续迭代 10 轮(简化计算,假设误差项保持不变):
| 迭代轮数 |  |  |
|---|---|---|
| 初始值 | 1.0 | 1.0 |
| 第1轮 | 1.8967 | 1.0587 |
| 第2轮 | 2.6923 | 1.1121 |
| ... | ... | ... |
| 第10轮 | 接近真实值 2.0 | 接近 0.0(被抑制) |
- 重要参数
:误差项持续推动其向真实值 2.0 靠近。
- 无关参数
:正则化逐步压缩,最终趋近于 0。
2.3.5 不同  的影响对比
的影响对比
 |  结果 结果 |  结果 结果 | 模型表现 |
|---|---|---|---|
| 0(无正则化) | 2.0 | 0.5(过拟合噪声) | 过拟合 |
| 0.1(适中) | 2.0 | 0.01 | 泛化能力好 |
| 1(过大) | 1.5 | 0.0 | 欠拟合(忽略特征) |
2.3.6 结论
的作用机制:
- 通过压缩项
抑制所有参数。
- 重要参数:误差项大,抵消压缩效果,保留合理值。
- 无关参数:误差项小,压缩效果主导,趋近于零。
- 通过压缩项
类比:正则化像“智能过滤器”:允许重要特征(误差项大)通过,抑制无关特征(误差项小)。

2.4 代价函数
2.4.1 正则化的核心思想
- 问题背景:当模型包含高阶项(如
)时,容易导致过拟合。
- 解决思路:通过修改代价函数,对高次项的系数(如
)施加惩罚,迫使这些参数趋近于零,从而简化模型。
2.4.2 正则化代价函数的定义
假设原始模型为:
修改后的代价函数:
- 第一项:原始均方误差(MSE),衡量模型对训练数据的拟合程度。
- 第二项:正则化项(L2正则化),惩罚所有参数
(
)的大小。
- 正则化参数
:控制惩罚力度。
越大,参数
被压缩得越小,模型越简单。
过大会导致欠拟合(如所有
,模型退化为常数
)。
2.4.3 正则化的作用原理
-
抑制过拟合:
- 通过惩罚高阶项(如
),减少模型对噪声的敏感度。
- 例如,若
,则
和
会被显著压缩,削弱高阶项的影响。
- 通过惩罚高阶项(如
-
自动特征选择:
- 对所有参数(除
)施加惩罚,让算法自动决定哪些特征需要保留或弱化。
- 对所有参数(除
2.4.4 正则化参数  的影响
的影响
| 场景 | 影响 | 结果 |
|---|---|---|
 | 无正则化,模型可能过拟合。 | 高方差,低偏差 |
 适中 适中 | 平衡拟合与泛化,参数适度减小。 | 模型复杂度适中 |
 过大 过大 | 所有参数  ( (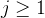 )趋近于零,模型退化为 )趋近于零,模型退化为  。 。 | 高偏差,欠拟合 |
2.5 正则化线性回归
2.5.1 梯度下降法
正则化线性回归的代价函数为:
其中 

参数更新规则
- 对
(无正则化):
- 对
(
)(含正则化):
关键点:
- 每次更新时,
会额外乘以
,逐步压缩其值。
越大,参数缩小幅度越大,模型越简单。
2.5.2 正规方程法
正则化后的正规方程通过修改矩阵运算直接求解最优参数:
其中:
- X 是
的设计矩阵(包含全1列
)。
- M 是
的对角矩阵M,第一行第一列为0(不惩罚
),其余对角线元素为1。
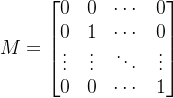
优势:
- 避免
不可逆的问题(即使特征间存在多重共线性)。
- 显式加入正则化项,直接控制模型复杂度。
2.5.3 对比与总结
| 方法 | 梯度下降 | 正规方程 |
|---|---|---|
| 适用场景 | 数据量大(如 m > 10,000) | 数据量小(如 m \leq 10,000) |
| 计算复杂度 | 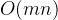 每次迭代 每次迭代 | 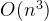 (矩阵求逆) (矩阵求逆) |
| 正则化实现 | 通过修改参数更新规则,逐步压缩参数值 | 通过修改矩阵运算,直接加入正则化项 |
| 优点 | 适合大规模数据,内存需求低 | 无需选择学习率,一步求解最优解 |
2.6正则化的逻辑回归模型
2.6.1 正则化后的代价函数
正则化逻辑回归的代价函数在原始对数损失函数基础上添加 L2 正则项:
- 核心项:
- 对数损失函数(衡量模型拟合能力)。
- L2 正则化项(抑制参数大小,防止过拟合)。
- 注意:正则化项 不包含截距项
。
2.6.2 梯度下降更新规则
梯度下降的更新分为两部分:
- 对
(无正则化)
- 对
(
)(含正则化)
关键点:
- 正则化通过压缩项
逐步缩小参数值。
- 仅对
的参数施加正则化,
始终自由更新。
2.6.3 Python 代码实现
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def cost_reg(theta, X, y, lambda_):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
# 计算对数损失
h = sigmoid(X * theta.T)
term1 = np.multiply(-y, np.log(h))
term2 = np.multiply((1 - y), np.log(1 - h))
loss = np.sum(term1 - term2) / len(X)
# 计算正则化项(排除 theta_0)
reg = (lambda_ / (2 * len(X))) * np.sum(np.power(theta[:, 1:], 2)) # theta[:,1:] 表示 j≥1 的参数
return loss + reg
def gradient_reg(theta, X, y, lambda_):
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
# 计算梯度
h = sigmoid(X * theta.T)
grad = (1 / len(X)) * X.T * (h - y) # 原始梯度
# 对 j≥1 的参数添加正则化项
grad[1:] += (lambda_ / len(X)) * theta[:, 1:].T # 注意索引从1开始
return grad.flatten()
2.6.4 与线性回归正则化的区别
尽管梯度下降公式形式相似,但二者本质不同:
| 差异点 | 逻辑回归 | 线性回归 |
|---|---|---|
| 假设函数 |  (Sigmoid 函数) (Sigmoid 函数) | 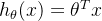 (线性) (线性) |
| 损失函数 | 对数损失(Log Loss) | 均方误差(MSE) |
| 梯度计算 | 梯度中包含 Sigmoid 函数的导数项 | 梯度为线性组合 |
2.6.5 正则化参数 的选择
的选择
交叉验证:通过网格搜索(如 GridSearchCV)选择最佳 
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import GridSearchCV
# 定义候选 λ 值(注意:sklearn 中参数名为 C,且 C = 1/λ)
param_grid = {'C': [0.001, 0.01, 0.1, 1, 10, 100]} # C 越小,正则化越强
# 使用网格搜索
model = LogisticRegression(penalty='l2', solver='liblinear')
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(X_train, y_train)
best_lambda = 1 / grid_search.best_params_['C'] # 转换为 λ

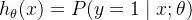
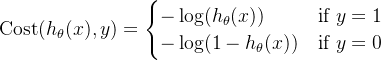
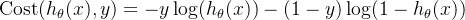
![J(\theta) = -\frac{1}{m} \sum_{i=1}^m \left[ y^{(i)} \log(h_\theta(x^{(i)})) + (1-y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9KJTI4JTVDdGhldGElMjk%3D%20%3D%20-%5Cfrac%7B1%7D%7Bm%7D%20%5Csum_%7Bi%3D1%7D%5Em%20%5Cleft%5B%20y%5E%7B%28i%29%7D%20%5Clog%28h_%5Ctheta%28x%5E%7B%28i%29%7D%29%29%20+%20%281-y%5E%7B%28i%29%7D%29%20%5Clog%281%20-%20h_%5Ctheta%28x%5E%7B%28i%29%7D%29%29%20%5Cright%5D)

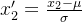

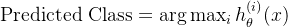
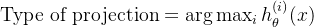

![J(\theta) = \frac{1}{2m} \left[ \sum_{i=1}^m \left( h_\theta(x^{(i)}) - y^{(i)} \right)^2 + \lambda \sum_{j=1}^n \theta_j^2 \right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9KJTI4JTVDdGhldGElMjk%3D%20%3D%20%5Cfrac%7B1%7D%7B2m%7D%20%5Cleft%5B%20%5Csum_%7Bi%3D1%7D%5Em%20%5Cleft%28%20h_%5Ctheta%28x%5E%7B%28i%29%7D%29%20-%20y%5E%7B%28i%29%7D%20%5Cright%29%5E2%20+%20%5Clambda%20%5Csum_%7Bj%3D1%7D%5En%20%5Ctheta_j%5E2%20%5Cright%5D)
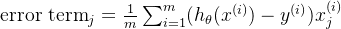






![J(\theta) = \frac{1}{m} \sum_{i=1}^m \left[ -y^{(i)} \log(h_\theta(x^{(i)})) - (1 - y^{(i)}) \log(1 - h_\theta(x^{(i)})) \right]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9KJTI4JTVDdGhldGElMjk%3D%20%3D%20%5Cfrac%7B1%7D%7Bm%7D%20%5Csum_%7Bi%3D1%7D%5Em%20%5Cleft%5B%20-y%5E%7B%28i%29%7D%20%5Clog%28h_%5Ctheta%28x%5E%7B%28i%29%7D%29%29%20-%20%281%20-%20y%5E%7B%28i%29%7D%29%20%5Clog%281%20-%20h_%5Ctheta%28x%5E%7B%28i%29%7D%29%29%20%5Cright%5D)

