DS
qwq
题单
1.P4374 Disruption P
solution:
发现新加入一条边会使得原来的图出现一个环,换上的边均可以被其代替,于是可以用树链剖分维护,每次加边相当于x到y之间加一条z,维护最小值即可
[Done]
2.P2590树上操作
solution:
树剖裸题
[Done]
3.CF1009F Dominant Indices
solution:
我们考虑树形dp,设 f u , d e p f_{u,dep} fu,dep表示u的子树中与 u u u的子树距离为 d e p dep dep的点数
转移为 f u , d e p = ∑ v 为 u 儿 子 f v , d e p − 1 f_{u,dep}=\sum\limits_{v为u儿子}f_{v,dep-1} fu,dep=v为u儿子∑fv,dep−1
考虑优化:通过长链剖分对于长儿子直接当做答案,其他的再暴力合并
[Done]
4.私题(9.25)date
大意:T组数据,每次维护1个1-n的序列,支持两种操作
- 是找多个区间使得sum最大,并在最大情况下的最小区间个数
2.支持单点修改
solution:
根据贪心思想,如果是正数那么就直接加,负数坑定不要,如果有0就看两边是不是正数,然后用线段树维护区间正数个数以及pre,nxt是否为正
[Done]
5.#21253. 「NOIP2021 国庆集训 B 组 Day1」序列修改
solution:
首先可以得到两个性质:
1.我们每次操作肯定是把 a x a_x ax改为 a y a_y ay
2.如果一个 a x a_x ax出现了两或多次,那么我们修改 a x i i > 1 a_{x_i}i>1 axii>1明显是不优的
于是最朴素的暴力思想出来了,直接枚举x,y,(x,y为 a x , a y a_x,a_y ax,ay第一次出现的位置)暴力修改计算取最小。(我会的)
我们进一步分析:
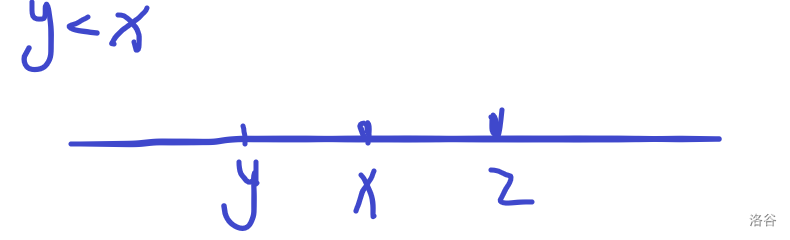
我们设 S i = ∑ j = i n j S_i=\sum\limits_{j=i}^{n}j Si=j=i∑nj,z为 a x a_x ax在原序列中下一个出现的位置(若 a x a_x ax仅出现一次则为n+1)
一下讨论均为 a x 变 为 a y a_x变为a_y ax变为ay
此时
c
[
x
,
z
)
]
c[x,z)]
c[x,z)]都减去1,因此新增的代价为
∣
a
x
−
a
y
∣
−
S
x
+
S
y
\left|a_x-a_y\right|-S_x+S_y
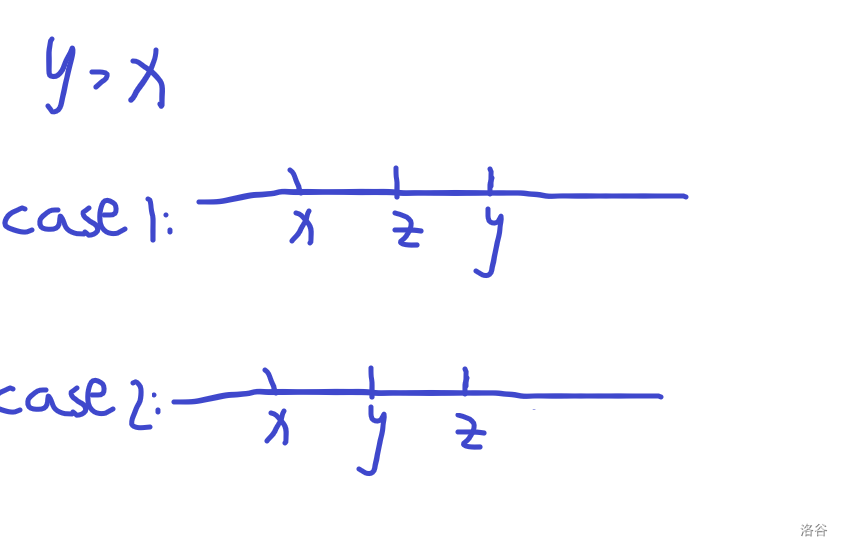
∣ax−ay∣−Sx+Sy因此选择与x差值最小的转移
case 1:修改会使
c
[
z
,
y
)
]
c[z,y)]
c[z,y)]加1,没用
case 2:修改会使 c [ y , z ] c[y,z] c[y,z]减1,新增代价为 ∣ a x − a y ∣ − S y + S x \left|a_x-a_y\right|-S_y+S_x ∣ax−ay∣−Sy+Sx
然后需要拆一下绝对值,决定方案
这样就可以 O ( n 2 ) O(n^2) O(n2)实现通过枚举x,y,配上前缀和优化暴力得到答案
然后我们发现第一类,发现绝对值以外部分只与x有关,而绝对值部分我们只需要知道x前面与 a x a_x ax绝对值最小的 a y a_y ay,用set维护
对于第二类,对
a
x
<
a
y
a_x<a_y
ax<ay和
a
x
>
a
y
a_x>a_y
ax>ay两种情况分析
树状数组维护两个前缀和,一个为“-”的,另外一个是“+”的,满足
S
y
+
a
y
S_y+a_y
Sy+ay类似的结构
有code
6. 「NOIP2021 国庆集训 B 组 Day4」偏序问题
solution:
我懒
(
稍微补充一点 b i t s e t bitset bitset的用法:
用处可以压缩时间空间复杂度,并且一般用于求集合的交并,bitset中数据以0/1存储。
- count():返回ture的数量
- size ():返回bitset的大小
- all():如果所有位都是ture就返回ture否则返回flase
- set():将整个bitset变成ture
- reset():全部变为flase
- flip():全部翻转
7. 「NOIP2021 国庆集训 B 组 Day4」排队问题
solution:
先从左到右按a作为关键词排序,然后先找出每个
a
i
a_i
ai有多少个
a
j
a_j
aj大于它记作
c
i
c_i
ci,如果存在
c
i
<
b
i
c_i<b_i
ci<bi那么必定无解,然后对与一个数,我们可以把它放在
b
i
b_i
bi的位置和
c
i
−
b
i
+
1
c_i-b_i+1
ci−bi+1两个位置上,又因为要求字典序最小的位置,那么我们肯定放小的地方(因为已经排过序了),用线段树维护序列的状态即可
code
8.P1823 Patrik 音乐会的等待
solution:
通过画图发现,一个人对于左边而言只能看到与之前第一个比自己大的人之间的人,于是可以维护一个单调递减的单调栈,二分查找那个人,每个人的贡献就可以无重复的求出来了[Done]
9.[NOIP 2021 国庆集训 雅礼联考 百鸽笼]
sol:
把序列倒过来,然后删去增加就相当于新建一个点了,于是就是一个裸的主席树了
code
10. 「NOIP2021 国庆集训 B 组 Day6」相似序列
solution:
考虑对区间每个数出现的个数进行hash并进行前缀和。对于询问就直接hash查询就可以了,如果完全相同,那么没毛病。但是不相同的话就要分类讨论了
1.对于管辖区间 [ a , b ] [a,b] [a,b]子串的树,如果只有左右儿子其一不同,就递归对应的子树
2.如果左右儿子都不相同,就要找到第一个和最后一个不同位置,并且期间不能有东西
主席树维护即可
code
11.P5490 扫描线
sol:
因为在解析几何中,矩形的面积可以表示为截线长度*扫过的高,那么我们可以把矩形的上面一条横线记作-1,下横线记作1,。然后我们把矩形的左右边界用x数组存储并排序去重离散化,就可以用线段树维护这离散化后的得到的线段(或者说原来就存在的线段,只不过可能相差太大导致爆空间所以离散化),维护的信息有这个区间被覆盖的次数以及被截的长度,然后扫描线从下往上扫,碰到线就更新相应的信息并计算贡献
12. 「NOIP2021 国庆集训 B 组 Day10」建造游戏
sol:
首先筛去从左指向右的边,然后发现如果增加一条从右指向左的边,就会形成环,环内的点是可以互相到达的,所以其中的点的值就全变成了这个区间的最大值。
但是这样不好维护删去的点,我们换个角度思考,每条
x
−
>
y
(
x
>
y
)
x->y(x>y)
x−>y(x>y)的边,就会导致区间
[
y
+
1
,
x
]
[y+1,x]
[y+1,x]内的所有点都可以到达y,于是把区间
[
y
+
1
,
x
]
[y+1,x]
[y+1,x]之间的点进行染色,于是问题就变成了,从一个点向左出发,只能走染过色的点,最远可以到达哪个点?二分或者直接递归。
code
13.NOIP 停课集训 Day 10 Can you answer the question 陆
sol:
经典平衡规划.我们对于不同的k有不同更优的复杂度写法。
1.对于 k < n k<\sqrt n k<n时的算法,我们可以每个k都维护前缀和
2.对于 k > n k>\sqrt n k>n时采用分块或者 n k \frac{n}{k} kn次线段树修改,每次修改区间 [ k ∗ j + l , m i n ( k ∗ j + r , n ) ] [k*j+l,min(k*j+r,n)] [k∗j+l,min(k∗j+r,n)]
查询时分别计算贡献,前缀和的话可能会导致很多重复的区间,所以我们需要重复计算贡献就是
(
j
/
r
−
j
/
l
)
(j/r-j/l)
(j/r−j/l)*前缀和,对于其他多余的部分,前缀和求和即可,其他就是个线段树的区间求和了
code
14. NOIP2021 冲刺集训 建造游戏
sol:
对于每个操作维护一个trie树,每个操作5的答案就是两个子树根节点的lca,然后对于多出来的4操作,发现只有最前面的不可匹配标记有影响,所以用一个set维护就可以了code
15.雅礼联考 倍数区间
sol:
awzc,我们考虑枚举每个
a
i
a_i
ai,然后二分找到最远的
L
i
,
R
i
L_i,R_i
Li,Ri,使得满足条件,区间gcd可以用线段树和st表
code st表版+线段树版
16.P1438 无聊的序列
sol:
考试上考了加强版,但是主体部分仍然不变。根据等差数列的性质,维护差分即可,只要在 s u m L sum_L sumL加上 K K K, s u m [ L + 1 , R ] sum_{[L+1,R]} sum[L+1,R]加上 D D D,尾部 a R + 1 a_{R+1} aR+1减去 ( k + ( r − l ) ∗ d ) (k+(r-l)*d) (k+(r−l)∗d)线段树维护就可以了。
结束了吗?当然没有,考场上的分块做法被杀掉了,但是真的被杀掉了吗?并没有。
我们充分运用人类的智慧,对于散块就可以暴力算值,对于整块(也是核心部分,考试卡的地方),我们直接维护S和D,最后暴力算答案就是
a
p
+
D
b
e
l
[
l
]
∗
(
l
−
l
e
b
e
l
[
l
]
)
+
S
b
e
l
[
l
]
a_{p}+D_{bel[l]}*(l-le_{bel[l]})+S_{bel[l]}
ap+Dbel[l]∗(l−lebel[l])+Sbel[l],好的仔细算了一下复杂度,
O
(
N
N
)
O(N \sqrt N)
O(NN),这题是没什么问题了,但是考试的题目好像还是不行qwq,只有五十,五十万的话只能带log
17.P3792 由乃与大母神原型和偶像崇拜
sol:
线段树维护区间最大值和区间最小值,然后根据数学公式知道 1 2 + 2 2 + 3 2 + … … + n 2 = n ∗ ( n + 1 ) ∗ ( 2 ∗ n + 1 ) 6 1^2+2^2+3^2+……+n^2=\frac{n*(n+1)*(2*n+1)}{6} 12+22+32+……+n2=6n∗(n+1)∗(2∗n+1),但是这样可能会溢出,所以我们考虑取模以及提前判断即若区间最大值与最小值的差与序列长度不相等的话就不用考虑了
18.字符串匹配
sol:
虽然看起来不像,但我的确把它放进了数据结构,这是NOIP原题,所以暴力分很充足。我先看到题面,我首先想到的暴力是暴力枚举C,然后找 ( A B ) i (AB)^i (AB)i显然这不是很优秀的暴力,因为我们完全可以枚举这个循环节 ( A B ) i (AB)^i (AB)i这样的话效率比枚举C更高也少了不少遗漏的情况。所以我们可以考虑枚举循环节长度,其上下界也不难得到为 ( 2 , n − 1 ) (2,n-1) (2,n−1),那我们设 S = ( A B ) k C S = (AB)^kC S=(AB)kC,在枚举k之前,我们需要补充一个前置知识:一个字符串的最小循环周期是 ∣ A ∣ − f a i l ∣ A ∣ |A|-fail_{|A|} ∣A∣−fail∣A∣,其中 f a i l ∣ A ∣ fail_{|A|} fail∣A∣表示字符串A的失配指针。我们考虑怎样的 ( A B ) k (AB)^k (AB)k是合法的,设 S 1 − S ∣ ( A B ) k ∣ S_{1}-S_{|(AB)^k|} S1−S∣(AB)k∣这个子串的最小循环周期为k,那么只要 k ∣ ∣ A B ∣ k||AB| k∣∣AB∣就能保证这个 ( A B ) k (AB)^k (AB)k是S的CP,是合法的。但是题目又给了一个限制条件 f ( A ) < f ( K ) f(A)<f(K) f(A)<f(K),发现可以维护出现奇数个字符数量的前后缀和,然后判断即可,可以用树状数组维护优化,这样的话这题就没了
19.CF380C Sereja and Brackets
sol:
用线段树维护区间的未匹配的左括号数,右括号数以及已经匹配的括号数目,pushup时需要注意减去已经配对的括号数目
20.Mex
sol:
大致题意:求连续子区间的最小未出现的自然数之和
如果固定左端点,随着右端点的递增,其mex值也是单调不降的。考虑数据结构优化暴力,枚举左端点,用线段树维护以点r为右端点的区间mex值。左端点右移时需要消除 a l a_l al的影响。
下面先分析 a l a_l al可以影响到的区间:设 a l a_l al下一次出现的位置是 n x t l nxt_l nxtl那么它影响的右端点肯定是 [ l , n x t l ) [l,nxt_l) [l,nxtl),且mex大于 a l a_l al这个结论显然。
被影响即我删去
a
l
a_l
al后这个以这个区间为右端点的mex将会变为
a
l
a_l
al,那么就是一个区间修改了,考虑到mex的单调不减性,可以二分找到这个区间就可以
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN)解决问题了
code
21.CF997E Good Subsegments
sol:
很容易知道好区间的定义是: max l < = x < = r − min l < = x < = r = = r − l \max\limits_{l<=x<=r}-\min\limits_{l<=x<=r}==r-l l<=x<=rmax−l<=x<=rmin==r−l,那么很暴力的思想就是将询问离线,按右端点排序,然后枚举右端点,计算左端点的答案。
采用扫描线的思想,枚举右端点时计算每个左端点的 ( m a x − m i n ) ∗ ( r − l ) (max-min)*(r-l) (max−min)∗(r−l)的最小值,若该区间最小值为0,那么贡献就是左端点在这个区间内时的好区间个数,然后新增一个t标记来记录当前最小值的贡献,每次移动右端点就全局t+1,表示没移动的区间造成的贡献,这样我们就可以就可以维护对于每个左端点,右端点小于等于当前处理的右端点时,好区间个数。那么每次更新询问的答案,只要区间查询即可
22.CF840D
sol:
好像是果的权值线段树,没什么好说的
基础算法
csp,我因为基础算法挂掉了,让我不得不警惕
1.CF3D Least Cost Bracket Sequence
sol:
一道看似字符串的贪心水题,带反悔的贪心。我们边处理边计算,先让扫到的‘?’边为’)’,那么我们只需要维护一个fuck来记录右大于左的数量,每次都让a-b最小的问号变为‘)’即可,并且要注意细节
2.CF965E Short Code
sol:
神题,建立trie树后,我们把每个字符串看做一个点,这个点可以向上跳,且点不相交,要求深度和最小。我们对每个点维护一个堆,当这个点为空时就把以他为根节点的子树里深度最大点跳到这里更新答案一直跳到堆为空即可
3.P2107 小Z的AK计划
sol:
考虑带反悔的贪心,先按x顺序扫一遍,放入堆中,然后如果目前的时间大于m就把堆中最大的值取出完成反悔操作,并且每次操作都取最大值
4.P7913 廊桥分配
sol:
一顿愚蠢的操作把自己搞成傻逼
显而易见的,多一个廊桥对于原来的贪心策略(飞机放在哪个廊桥没有影响),所以我们可以分别算出对于每个飞机而言,按贪心会放在哪个廊桥,并且从而统计出分配给x个给国内/国外时的答案,最后取最大和。对于贪心,维护两个堆,一个维护时间使得飞机的站尽量靠前,另一个则维护空闲的廊桥
5.P5502 最大公约数
sol:
枚举左端点,当区间gcd不变的时候希望区间长度尽量大,而右端点右移以为其gcd必然单调不增所以可以倍增找到,因为gcd可以区间维护
6.CF545C Woodcutters
sol:
简单贪心,如果能左就左,不然向右,不然不放
7.CF446B
sol:
很容易猜到的结论(我是通过小的部分分想到的),操作顺序与最优性无关(m=1),每次选最大的行或者列,最后计算答案时,设对横的操作次数为x,那么列的就是k-x,答案要减去 ( k − x ) ∗ x ∗ p (k-x)*x*p (k−x)∗x∗p,用堆维护,算出进行x次横或者列操作时的贡献
8.P4653
sol:
贪心选择双指针维护即可
9.P2906
sol:
套路:看见曼哈顿距离就变成切比雪夫距离
转完后的新坐标需要满足x之差绝对值和y之差绝对值小于等于C,用队列和set维护,并查集维护联通性
10.CF3B
sol:
考虑暴力枚举选1的个数剩下的选2的,然后更新答案,贪心选择
11.CF33C
sol:
设前缀为A,重复部分为C,后缀为B,A+B+C=S,题目要最大化C-(A+B),
又A+B=S-C,故原式为:2*C-S,问题变为求最大子段和
12.CF235A
sol:
喵喵题,首先我们知道任意两个相邻的自然数是互质的因为根据 g c d ( a , b ) = g c d ( b , a − b ) gcd(a,b)=gcd(b,a-b) gcd(a,b)=gcd(b,a−b)即可得证,那么两个数时的最大答案肯定是 n ∗ ( n − 1 ) n*(n-1) n∗(n−1),于是进一步证明发现当n为奇数的时候有 g c d ( n , n + 2 ) gcd(n,n+2) gcd(n,n+2)也是1,意思是说当n为奇数的时候答案就是 n ∗ ( n − 1 ) ∗ ( n − 2 ) n*(n-1)*(n-2) n∗(n−1)∗(n−2)而n为偶数的时候最大的两个肯定要选那么第三个就肯定是 ( n − 3 ) (n-3) (n−3)了,证明简单
13.P3154
sol:
数据范围小考虑暴力搜索+剪枝,众所周知:比赛问题的搜索思路是1V2,1V3,……,1VN,2V3…….然后考虑优化:
1.胜局和平局是可以算出来的:
s + p = ( n − 1 ) ∗ n / 2 s+p=(n-1)*n/2 s+p=(n−1)∗n/2
3 ∗ s + 2 ∗ p = s u m 3*s+2*p=sum 3∗s+2∗p=sum
2.由上可知,我们可以通过平局和胜利来剪枝而分数大的队伍更加倾向于胜利或平局,于是可以从大往小搜索
3.若目前剩下的局面(即每个对于离目标的差值)已经出现过就不用再往下走直接记忆化就可以了(HASH)
14.CF364B
sol:
首先我们可以知道贪心策略:每天尽量换到价值大的,这样我们以后的价值会更高,于是可以做一遍0/1背包,然后枚举天数求出每天可以得到的最大价值,如果无法更新了那么就是最终答案
15.CF425A
sol:
直接暴力枚举区间,然后每次交换区间内最小以及区间外最大,取max
16.CF1066D
sol:
直接二分答案,然后 O ( N ) O(N) O(N)检验,复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)
17.CF1041C
sol:
容易知道每次选最小的一定是最优的,于是我们直接set或者multiset维护即可
18.CF1029C
sol:
知道交集肯定是 [ max ( l ) , min ( r ) ] [\max(l),\min(r)] [max(l),min(r)],所以我们可以暴力枚举删除线段然后维护最大次大值即可
19.CF457C
sol:
发现票数与最终答案成正向关所以可以二分答案?然后贪心策略显然:如果一个人的票数比答案高就从小到大取直到比自己少,然后再从其他人中选
20.CF1005D
sol:
由朴素dp方程然后根据同余系优化转移范围
21CF962D
sol:
喵喵题,根据题意模拟一遍,用堆维护,每次取两次堆首,若不相等第一个肯定是最终序列,否则继续
22.CF95C
sol:
只有1000个点所以可以直接每个点跑dj然后求出t步之内可以到达的点然后建出新图跑最短路即可
23.CF22C
(喵喵构造题)
24.CF95C
(先跑一遍最短路找出新图,然后在新图上跑一遍最短路就是答案记得数组开大)
25.CF891C
(不写了,屑题)
26.CF913D
(直接对t排序,然后从小到大选择,如果 a [ i ] a[i] a[i]<k直接丢掉就可以了)
27.P2501
(trick题:trick1:若要使一个区间单调不降,那么需要存在一个k使得 b i = b l ( i ≤ k ) , b j = b r ( j ≤ k ) b_i=b_l(i\le k),b_j=b_r(j\le k) bi=bl(i≤k),bj=br(j≤k),此时的代价最小,证明感性,用人话讲就是你会找到一个中转点前面和l相同,后面和r相同)
28.P3620
(X倍经验,把两栋楼之间的空隙作为点,点权为两点距离,然后问题变为求(n-1)中选k个不相邻的点的最小代价,反悔贪)
29.CF939F
(dp,设dp[i][j]表示前i秒,当前处理正面,反面处理了j秒的最小翻面次数)
30.CF449C
(经典题目,从大到小枚举质数,然后统计没被匹配的倍数,若为偶数则两两匹配否则去掉2*x,这样可以保证都被尽量匹配)
31.CF711D
(tarjan判环以后直接数环个数得到答案即可)
32.CF652D
(离散化后按右端点排序,对于每个左端点数有多少个区间的左端点在自己的右边即为答案)
33.CF6E
(st表维护区间最大最小值,然后枚举左端点,二分找右端点更新答案)
34.CF7D
(设dp[i]表示前缀i的阶级,那么 d p [ i ] = ( 0 , d p [ i 2 ] + 1 ) dp[i]=(0,dp[\frac{i}{2}]+1) dp[i]=(0,dp[2i]+1)取决于i是否为回文)
34.CF117C
(竞赛图三元环,枚举两个点,然后判断与i相邻的点是否与其成环)
35.P2749
(主要难点在于克服苦难主动拆分问题,判断相似可以通过联通块内两点两两之间的距离和,或者块的横长与纵长以及块的大小+这个图形内最远距离的两点之间的距离(二维凸包)进行判断)
36.P4090
(绝赞思维二分题,但是因该是恶意评价了,显然的结论是如果一头牛不行后面的都不行,因为一头牛不行当且仅当前面的牛形成循环,所以满足单调性)
37.CF913C
(认为是完全背包结果是贪心二分系列,发现题目有 2 ( i − 1 ) 2^(i-1) 2(i−1)那么必然与2进制相关,如果两个i的代价比一个i+1的小那么就用两个i代替之,然后二分钱即可)
38.CF721D
(每次选绝对值最小的,然后分复数个数进行讨论即可)
39.CF1374E2
(先按朴素的贪心策略得到答案,然后大力分类讨论)
40.CF1256D
(肯定是找到0然后尽量往前面移动)
41.CF140C
(优先队列+桶维护,每次找最大的三个然后注意细节即可)