文章目录
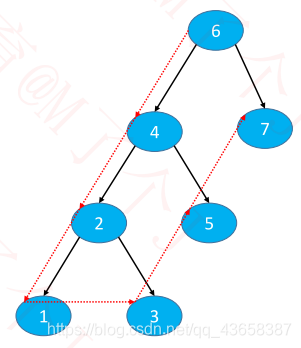
preorder
一路向左走,当访问节点为null时,转向右边
◼ 利用栈实现
- 设置 node = root
- 循环执行以下操作
如果 node != null
✓ 对 node 进行访问
✓ 将 node.right 入栈
✓ 设置 node = node.left
如果 node == null
✓ 如果栈为空,结束遍历
✓ 如果栈不为空,弹出栈顶元素并赋值给 node
最终前序遍历:6421357,但是总是先从根节点开始访问,所以对于357根节点发现其访问顺序和前序遍历顺序正好相反,则考虑使用栈
栈中保存的全部都是右子节点,所以当第一次出栈时,弹出3,此时处理3和处理6的逻辑相同,继续循环
public void preorder(Visitor<E> visitor) {
if (visitor == null || root == null) return;
Node<E> node = root;
Stack<Node<E>> stack = new Stack<>();
while (true) {
if (node != null) {
// 访问node节点
if (visitor.visit(node.element)) return;
// 将右子节点入栈
if (node.right != null) {
stack.push(node.right);
}
// 向左走
node = node.left;
} else if (stack.isEmpty()) {
return;
} else {
// 处理右边
node = stack.pop();
}
}
}
- 将 root 入栈
- 循环执行以下操作,直到栈为空
弹出栈顶节点 top,进行访问
将 top.right 入栈
将 top.left 入栈
public void preorder(Visitor<E> visitor) {
if (visitor == null || root == null) return;
Stack<Node<E>> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node<E> node = stack.pop();
// 访问node节点
if (visitor.visit(node.element)) return;
if (node.right != null) {
stack.push(node.right);
}
if (node.left != null) {
stack.push(node.left);
}
}
}
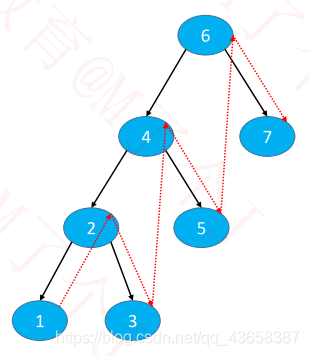
inorder
中序遍历:1234567,访问节点的顺序6421,但是其遍历顺序正好相反,即仍使用栈
栈中保存的全部都是父节点,所以当第二次出栈时,弹出2,访问其右节点3,处理逻辑与6相同,继续循环
public void inorder(Visitor<E> visitor) {
if (visitor == null || root == null) return;
Node<E> node = root;
Stack<Node<E>> stack = new Stack<>();
while (true) {
if (node != null) {
stack.push(node);
// 向左走
node = node.left;
} else if (stack.isEmpty()) {
return;
} else {
node = stack.pop();
// 访问node节点
if (visitor.visit(node.element)) return;
// 让右节点进行中序遍历
node = node.right;
}
}
}
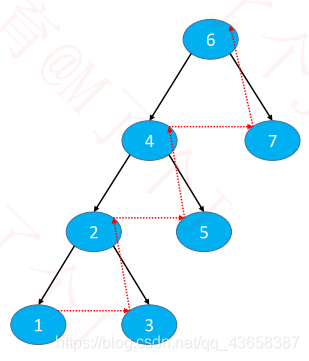
postorder
◼ 利用栈实现
- 将 root 入栈
- 循环执行以下操作,直到栈为空
如果栈顶节点是叶子节点 或者 上一次访问的节点是栈顶节点的子节点(即子节点已经访问过)
✓ 弹出栈顶节点,进行访问
否则
✓ 将栈顶节点的right、left按顺序入栈
后序遍历:1325476,访问顺序6421,依然相反,即使用栈,注意此时遍历顺序为476,所以入栈顺序为674
public void postorder(Visitor<E> visitor) {
if (visitor == null || root == null) return;
// 记录上一次弹出访问的节点
Node<E> prev = null;
Stack<Node<E>> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node<E> top = stack.peek();
if (top.isLeaf() || (prev != null && prev.parent == top)) {
prev = stack.pop();
// 访问节点
if (visitor.visit(prev.element)) return;
} else {
if (top.right != null) {
stack.push(top.right);
}
if (top.left != null) {
stack.push(top.left);
}
}
}
}
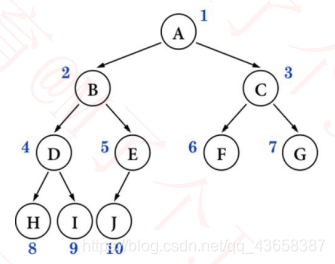
level order
◼ 实现思路:使用队列
- 将根节点入队
- 循环执行以下操作,直到队列为空
将队头节点 A 出队,进行访问
将 A 的左子节点入队
将 A 的右子节点入队
public void levelOrder(Visitor<E> visitor) {
if (root == null || visitor == null) return;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
if (visitor.visit(node.element)) return; // 访问节点
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
isComplete
完全二叉树(Complete Binary Tree)
◼ 完全二叉树:对节点从上至下、左至右开始编号,其所有编号都能与相同高度的满二叉树中的编号对应
◼ 叶子节点只会出现最后 2 层,最后 1 层的叶子结点都靠左对齐
◼ 完全二叉树从根结点至倒数第 2 层是一棵满二叉树
◼ 满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
完全二叉树的性质
◼ 度为 1 的节点只有左子树
◼ 度为 1 的节点要么是 1 个,要么是 0 个
◼ 同样节点数量的二叉树,完全二叉树的高度最小
◼ 假设完全二叉树的高度为 h ( h ≥ 1 ),那么
至少有 2h − 1 个节点 ( 20 + 21 + 22 + ⋯ + 2h−2 + 1 )
最多有 2h − 1 个节点( 20 + 21 + 22 + ⋯ + 2h−1 ,满二叉树 )
总节点数量为 n
✓ 2h − 1 ≤ n < 2h
✓ h − 1 ≤ log2n < h
✓ h = floor( log2n ) + 1
◼ 如果一棵完全二叉树有 768 个节点,求叶子节点的个数
假设叶子节点个数为 n0,度为 1 的节点个数为 n1,度为 2 的节点个数为 n2
总结点个数 n = n0 + n1 + n2,而且 n0 = n2 + 1 (每个节点都有父结点,但是根节点没有)
✓ n = 2n0 + n1 – 1
完全二叉树的 n1 要么为 0,要么为 1
✓ n1为1时,n = 2n0,n 必然是偶数
➢ 叶子节点个数 n0 = n / 2,非叶子节点个数 n1 + n2 = n / 2
✓ n1为0时,n = 2n0 – 1,n 必然是奇数
➢ 叶子节点个数 n0 = (n + 1) / 2,非叶子节点个数 n1 + n2 = (n – 1) / 2
叶子节点个数 n0 = floor( (n + 1) / 2 ) = ceiling( n / 2 )
非叶子节点个数 n1 + n2 = floor( n / 2 ) = ceiling( (n – 1) / 2 )
因此叶子节点个数为 384
◼ 一棵有 n 个节点的完全二叉树(n > 0),从上到下、从左到右对节点从 0 开始进行编号,对任意第 i 个节点
如果 i = 0 ,它是根节点
如果 i > 0 ,它的父节点编号为 floor( (i – 1) / 2 )
如果 2i + 1 ≤ n – 1 ,它的左子节点编号为 2i + 1
如果 2i + 1 > n – 1 ,它无左子节点
如果 2i + 2 ≤ n – 1 ,它的右子节点编号为 2i + 2
如果 2i + 2 > n – 1 ,它无右子节点
按索引找到第一个叶子节点,之后所有节点都是叶子节点
判断一棵树是否为完全二叉树
◼ 如果树为空,返回 false
◼ 如果树不为空,开始层序遍历二叉树(用队列)
如果 node.left!=null,将 node.left 入队
如果 node.left=null && node.right!=null,返回 false (此时度为1,那么为J,只能是left不为空right为空)
如果 node.right!=null,将 node.right 入队
如果 node.right=null
✓ 那么后面遍历的节点应该都为叶子节点,才是完全二叉树
✓ 否则返回 false
遍历结束,返回 true
public boolean isComplete() {
if (root == null) return false;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
boolean leaf = false;
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
if (leaf && !node.isLeaf()) return false;
if (node.left != null) {
queue.offer(node.left);
} else if (node.right != null) {
return false;
}
if (node.right != null) {
queue.offer(node.right);
} else { // 后面遍历的节点都必须是叶子节点
leaf = true;
}
}
return true;
}
height
递归
整个树的高度 = 左子树高度和右子树高度的最大值 + 1(父节点 )
public int height() {
return height(root);
}
private int height(Node<E> node) {
if (node == null) return 0;
return 1 + Math.max(height(node.left), height(node.right));
}
迭代
层序遍历的特点:每扫描完一层,树的高度+1,即遍历完所有节点,就求出树的高度
要记录每一层的节点数量,每次从队列中出队一个节点,levelsize–
当levelsize==0时意味着该层已经遍历完,要继续访问下一层,并重新赋值levelsize
public int height() {
if (root == null) return 0;
// 树的高度
int height = 0;
// 存储着每一层的元素数量
int levelSize = 1;
Queue<Node<E>> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node<E> node = queue.poll();
levelSize--;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
if (levelSize == 0) { // 意味着即将要访问下一层
levelSize = queue.size();
height++;
}
}
return height;
}
Reference:小码哥MJ