一、题目描述
请你设计并实现一个满足LRU(最近最少使用)缓存约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity)以正整数作为容量capacity初始化LRU缓存。int get(int key)如果关键字key存在于缓存中,则返回关键字的值,否则返回-1。void put(int key, int value)如果关键字key已经存在,则变更其数据值value。如果不存在,则向缓存中插入该组key-value。如果插入操作导致关键字数量超过capacity,则应该逐出最久未使用的关键字。
函数 get 和 put 必须以
O
(
1
)
O(1)
O(1) 的平均时间复杂度运行。
示例 1:
输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
二、题解
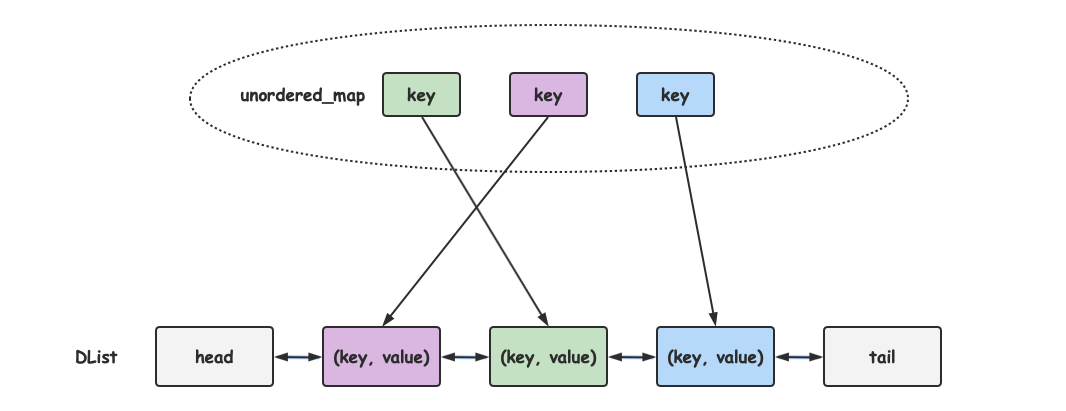
key 和 value 通过双链表(DList)存储,最近访问的放队头,每次删除都删除队尾即可。但仅凭这个链表无法实现
O
(
1
)
O(1)
O(1) 的 get 和 put,因此还需要一个映射了 key 和双链表节点位置的哈希表(unordered_map)。
二者的对应关系大致如下:
/**
* Your LRUCache object will be instantiated and called as such:
* LRUCache* obj = new LRUCache(capacity);
* int param_1 = obj->get(key);
* obj->put(key,value);
*/
/**
* 双链表节点类
*/
class DListNode {
public:
int m_key, m_value; // 数据域
DListNode *m_front, *m_back; // 指针域
DListNode(int key, int value) {
m_key = key;
m_value = value;
m_front = nullptr;
m_back = nullptr;
}
};
/**
* 双链表类
*/
class DList {
public:
DListNode *m_head, *m_tail; // 头节点和尾节点
DList() {
m_head = new DListNode(0, 0);
m_tail = new DListNode(0, 0);
m_head->m_back = m_tail;
m_tail->m_front = m_head;
}
/**
* 向双链表开头插入新节点并返回新节点的地址
* @param key
* @param value
* @return
*/
DListNode *push_front(int key, int value) const {
auto *new_node = new DListNode(key, value);
new_node->m_front = m_head;
new_node->m_back = m_head->m_back;
m_head->m_back->m_front = new_node;
m_head->m_back = new_node;
return new_node;
}
/**
* 删除节点并将指针置空
* @param node_ptr 指向待删除节点的指针的引用
*/
void erase(DListNode *&node_ptr) {
node_ptr->m_front->m_back = node_ptr->m_back;
node_ptr->m_back->m_front = node_ptr->m_front;
delete node_ptr;
node_ptr = nullptr;
}
/**
* 删除双链表队尾的元素并返回对应的key
* @return
*/
int pop_back() {
auto tmp = m_tail->m_front;
int ret = tmp->m_key;
m_tail->m_front = tmp->m_front;
tmp->m_front->m_back = m_tail;
delete tmp;
return ret;
}
~DList() {
delete m_head;
delete m_tail;
}
};
class LRUCache {
private:
int m_size; // 实际大小
int m_capacity; // 最大容量
DList m_list; // 存放key和value的双向链表
unordered_map<int, DListNode *> m_map; // 存放key的对应双链表节点地址的哈希表
public:
LRUCache(int capacity) {
m_size = 0;
m_capacity = capacity;
}
int get(int key) {
if (m_map.find(key) != m_map.end()) { // 对应key在缓存命中,需要将对应节点移到队头,并修改对应的map映射
int value = m_map.find(key)->second->m_value; // 保存value的临时变量
m_list.erase(m_map.find(key)->second); // 从队尾删除
m_map.at(key) = m_list.push_front(key, value); // 从队头插入并修改map映射
return m_map.find(key)->second->m_value; // 返回查询结果
}
return -1;
}
void put(int key, int value) {
if (m_map.find(key) != m_map.end()) { // 对应key在缓存命中,此时不需要插入,而需要将对应节点移到队头,并修改对应的map映射
m_list.erase(m_map.find(key)->second); // 从队尾删除
m_map.at(key) = m_list.push_front(key, value); // 从队头插入并修改map映射
} else { // 对应key在缓存未命中,此时需要进行插入
if (m_size < m_capacity) { // 缓存还没有满,直接插入
m_map.emplace(key, m_list.push_front(key, value));
m_size++;
} else { // 缓存已满,要根据LRU策略进行删除后再插入
m_map.erase(m_list.pop_back());
m_map.emplace(key, m_list.push_front(key, value));
}
}
}
};