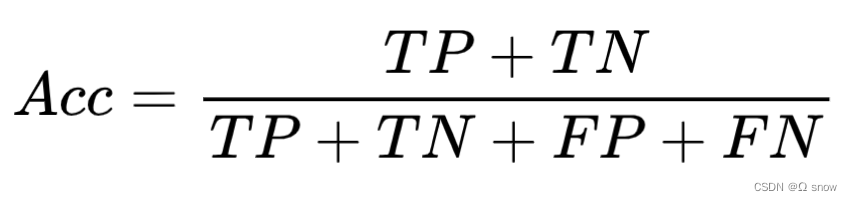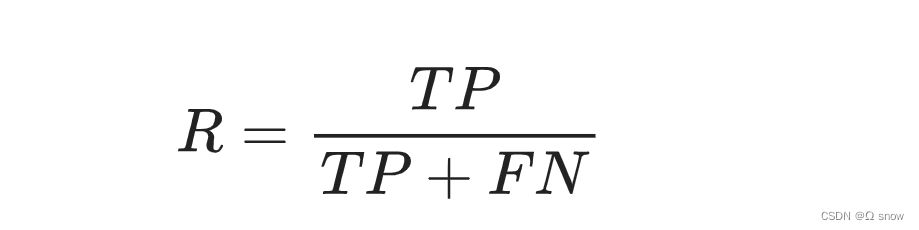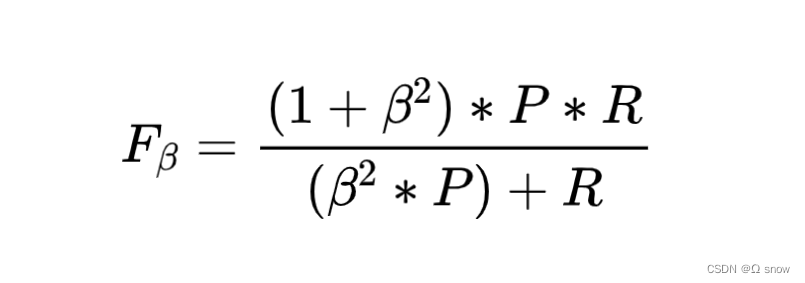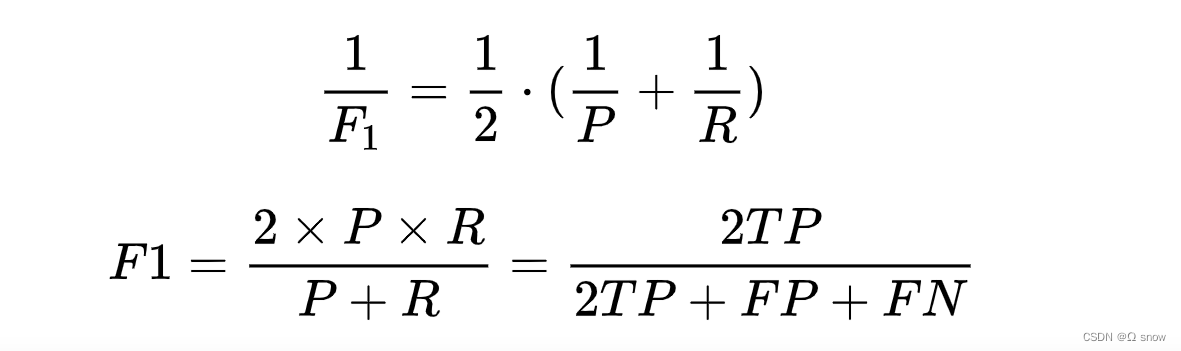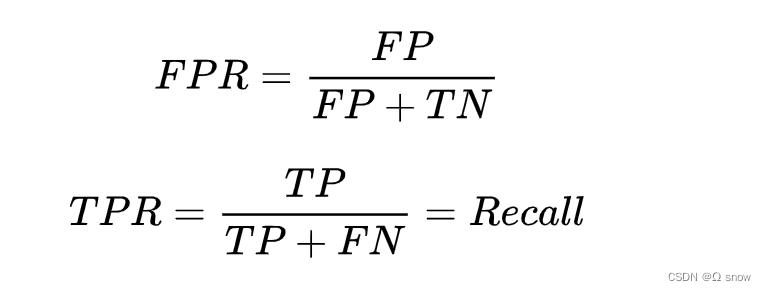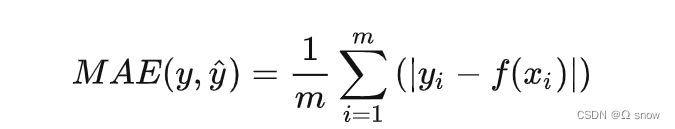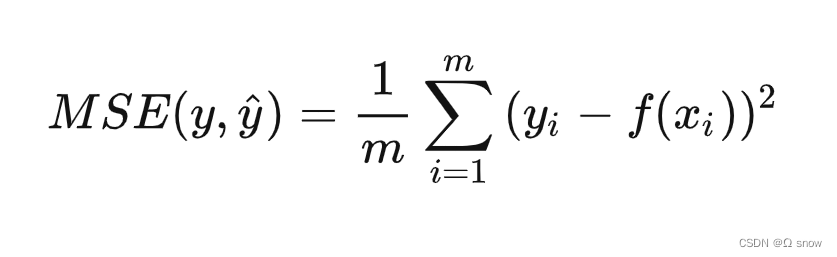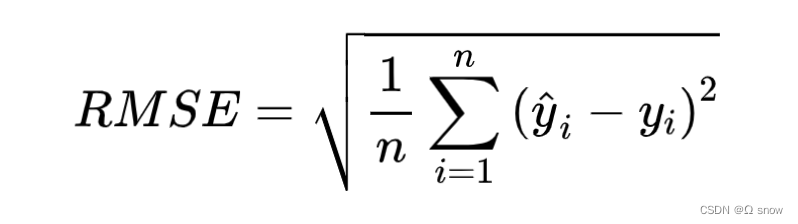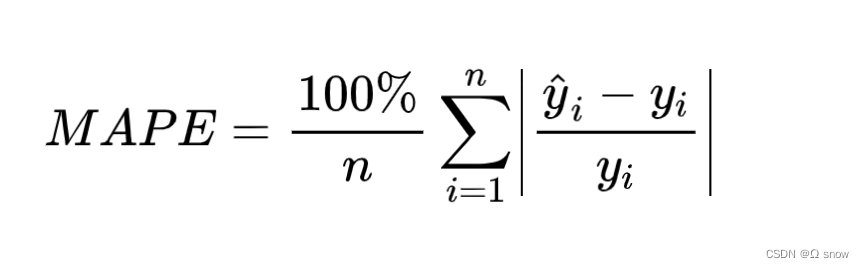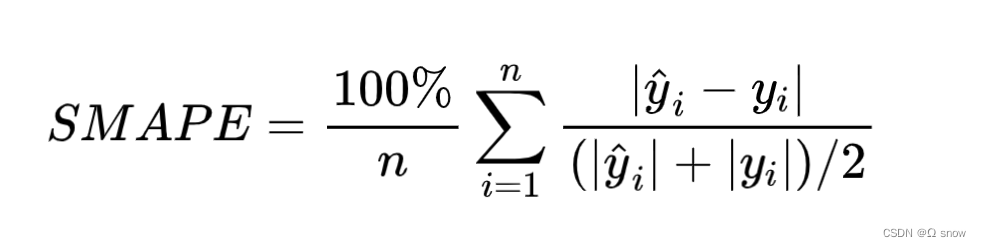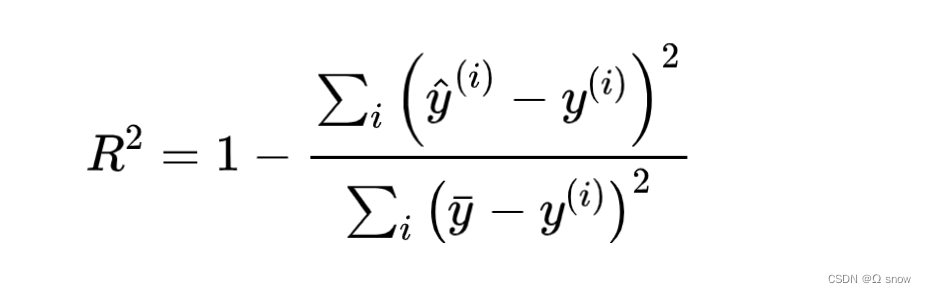深度学习分类、回归问题评价指标
在评估不同的机器学习模型的好坏时,需要用到一些评价和指标。其中有监督学习主要包括两类:分类问题和回归问题。可以根据两者输出类型不同,进行简单区别。
- Classification 分类: 给定类别选项,函数输出正确选项,单选或者多选。输出是类别,离散值。
- Regression 回归:函数的output是数字(scalar),可以选择线性模型,或者非线性模型。输出是数字,连续值。
一、分类评价指标
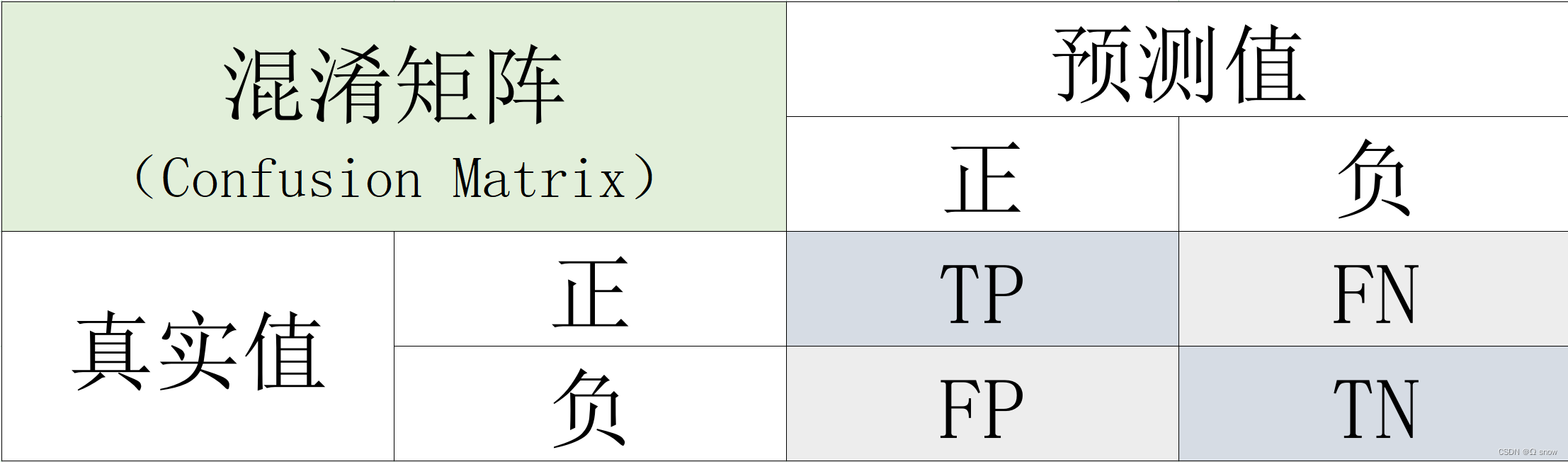
1.1混淆矩阵
混淆矩阵一般不会直接作为评价指标,但是他定义了常用指标中的一些符合的含义,以二分类问题为例,矩阵表现形式如下:
confusion_matrix()函数的输出格式为:
P(Positive)和N(Negative)代表模型的判断结果;T(True)和F(False)评价模型的判断结果是否正确。
混淆矩阵的
对角线表示判断正确,其余表示判断错误。
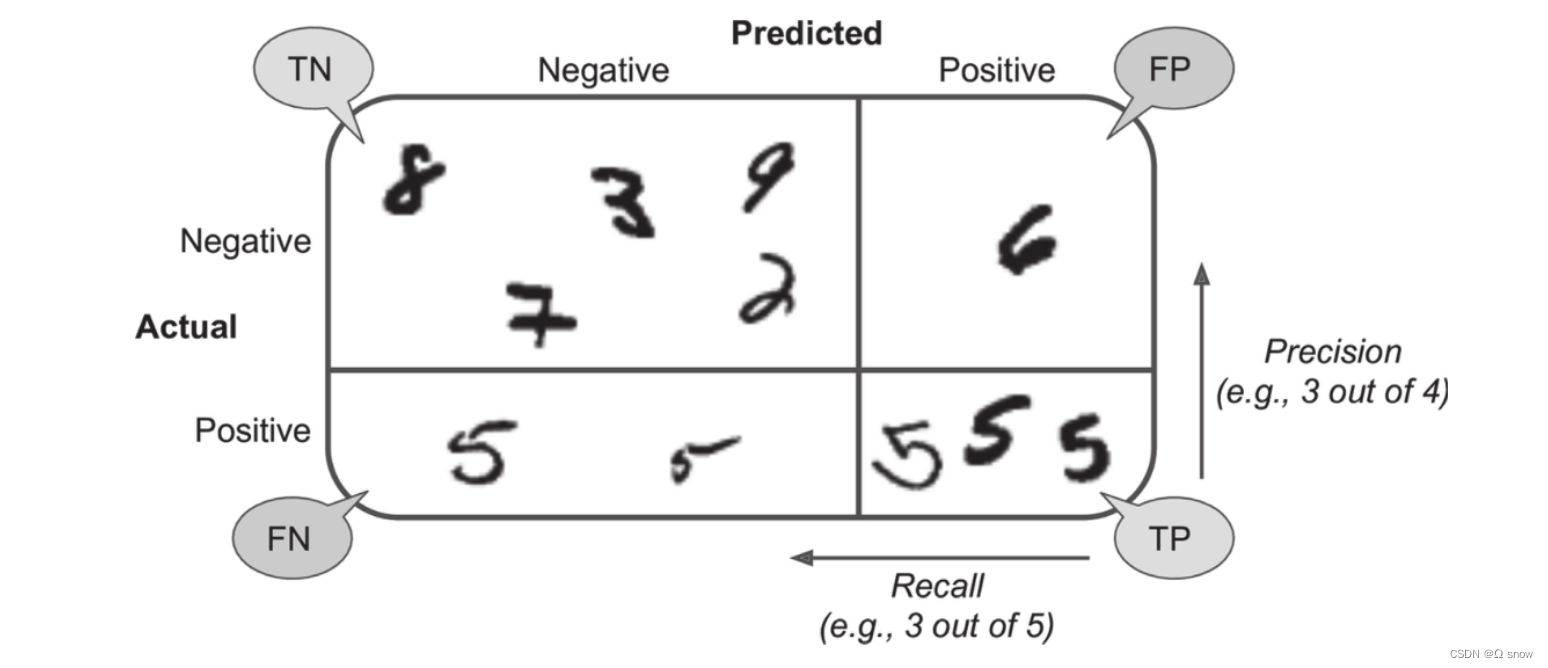
假设待检测事件为是否会发生故障:(故障为正样本)
- TP (True Positive):正确识别出故障;(T:结果正确,P:故障发生)
- FP(False Positive):检测出故障,实际未发生故障(错误检测);
- FN(False Negative):有故障,但未识别出;
- TN(True Negative):正确检测出未发生故障
模型训练的目标是降低FP和FN,至于具体是哪一个,需要看具体的需求。
- 降低假正例(FP):假设在垃圾邮件分类任务中,垃圾邮件为正样本。如果我们收到一个正常的邮件,比如某个公司或学校的offer,模型却识别为垃圾邮件(FP),那将损失非常大。所以在这种任务中,需要尽可能降低假正例。
- 降低假负数例(FN):假设在一个癌症检测问题中,每100个人中就有5个人患有癌症。在这种情况下,即使是一个非常差的模型也可以为我们提供95%的准确度。但是,为了捕获所有癌症病例,当一个人实际上没有患癌症时,我们可能最终将其归类为癌症。因为它比不识别为癌症患者的危险要小,因为我们可以进一步检查。但是,错过癌症患者将是一个巨大的错误,因为不会对其进行进一步检查。
1.2准确率(Accuracy)
准确率(Accuracy):在所有样本中,有多少样本被正确检测
注:Accuracy适合样本类别均衡的情况,在样本不平衡的情况下,产生效果较差。假设我们的训练数据中只有2%的正样本,98%的负样本,那么如果模型全部预测为负样本,准确率便是98%,。分类的准确率指标很高,呈现出模型很好的假象。
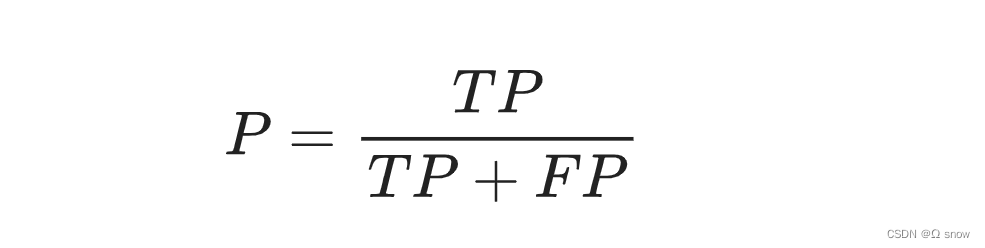
1.3精确率(Precision)
Precision(精准率):又称查准率,预测为正例的样本中有多少实际为正。即你认为的正样本,有多少是猜对的。
注:准确率可以反映一个类别的预测正确率。
1.4召回率(Recall)
Recall(召回率):又称查全率,实际为正例的样本有多少被预测为正。即正样本有多少被找出来了(召回了多少),召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。
注:召回率可以衡量模型找到所有相关目标的能力,即模型给出的预测结果最多能覆盖多少真实目标。召回率和精确率都只能衡量检索性能的一个方面,是一对矛盾的指标,当召回率高的时候,精确率一般很低;精确率高时,召回率一般很低。
1.5 F 1 {F}_{1} F1分数(F-Score,调和平均)和 F β {F}_{β} Fβ(加权调和平均)
F1是基于精确率和召回率的调和平均,又称为F-Score
- β>1:召回率(Recall)影响更大,eg. F 2 {F}_{2} F2
- β<1:精确率(Precision)影响更大,eg. F 0.5 {F}_{0.5} F0.5
β=1时,得到F1如下:
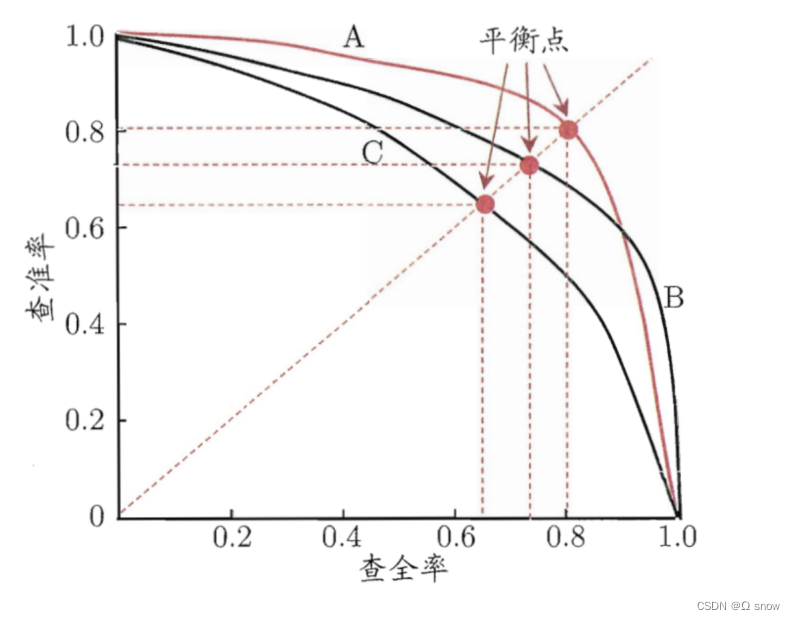
1.6 P-R曲线与AP、mAP
P-R曲线:通过选择不同的阈值,得到Recall和Precision,以Recall为横坐标,Precision为纵坐标得到的曲线图。
PR曲线性质:
- 如果一个学习器的P-R曲线被另一个学习器的曲线完全包住,后者性能优于前者;
- 如果两个学习器的曲线相交,可以通过平衡点(如上图所示)来度量性能;
- 如果有个划分点可以把正负样本完全区分开,那么P-R曲线面积是1*1;
阈值下降:
- Recall:不断增加,因为越来越多的样本被划分为正例,假设阈值为0.,全都划分为正样本了,此时recall为1;
- Precision:正例被判为正例的变多,但负例被判为正例的也变多了,因此precision会振荡下降,不是严格递减;
AP(average precision):Precision-recall 曲线下围成的面积,一般一个分类器性能越好,AP值越高。
mAP(mean average precision):多个类别AP的平均值。
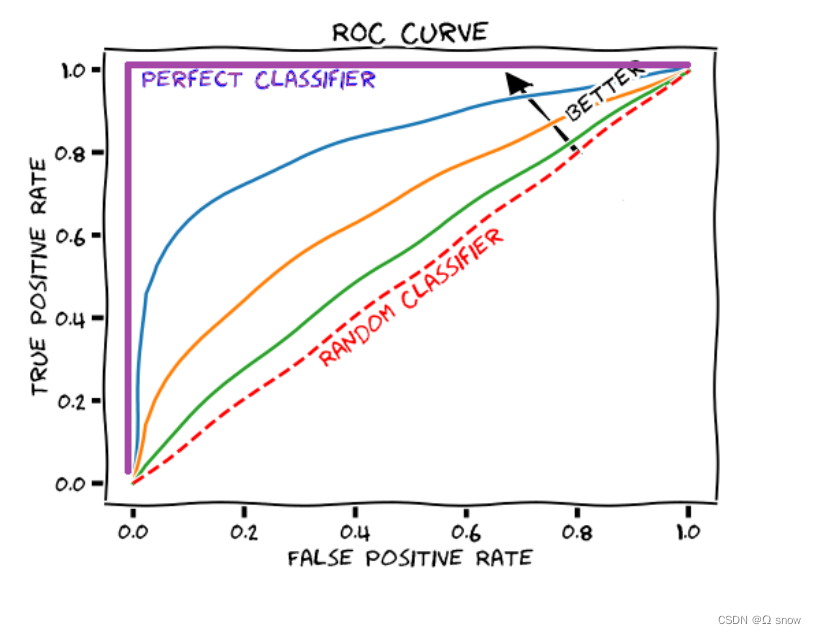
1.7 ROC-AUC
ROC(Receiver Operating Characteristic)曲线:曲线的横坐标为假正例率(FPR),即实际为负的样本有多少被预测为正;纵坐标为TPR(真正例率),即实际为正的样本多少被预测为正。
TPR和FPR的范围均是[0,1],通过选择不同的阈值得到TPR和FPR,然后绘制ROC曲线。
AUC (Area under Curve):即ROC曲线下的面积,介于0.1和1之间,作为数值可以直观的评价分类器的好坏,值
越大越好。
二、回归评价指标
2.1 MAE平均绝对误差
MAE(Mean Absolute Error):计算每一个样本的预测值和真实值的差的绝对值,然后求和再取平均值。
其中, y i {y}_{i} yi为真实值, y ^ \hat{y} y^ 和 f ( x i ) f{(x}_{i}) f(xi)为为模型的预测值。
2.2 MSE均方误差
MSE(Mean Square Error): 计算每一个样本的预测值与真实值差的平方,然后求和再取平均值
2.3 RMSE根均方误差
RMSE(Root Mean Square Error):在均方误差MSE的基础上开方
注:取均方误差的平方根可以使得量纲一致,这对于描述和表示是有意义的
2.4 MAPE平均绝对百分别误差
MAPE(Mean Absolute Percentage Error):计算对相对误差损失的预期。所谓相对误差,就是绝对误差和真值的百分比
注:当真实值有数据等于0时,存在分母0除问题,该公式不可用!
2.6 SMAPE对称平均绝对百分比误差
SMAPE(Symmetric Mean Absolute Percentage Error):
注:真实值、预测值均等于0时,存在分母为0,该公式不可用!
2.7 R 2 {R}^{2} R2决定系数
R 2 {R}^{2} R2 决定系数(Coefficient of determination): 被称为最好的衡量线性回归法的指标。
关于公式:
- 分母代表baseline(平均值)的误差,分子代表模型的预测结果产生的误差;
- 预测结果越大越好, R 2 {R}^{2} R2 为1说明完美拟合, R 2 {R}^{2} R2 为0说明和baseline一致;
使用同一个算法模型,解决不同的问题时,由于不同的数据集的量纲不同,MSE、RMSE等指标不能体现此模型针对不同问题所表现的优劣,无法判断模型更适合预测哪个问题。
R
2
{R}^{2}
R2 得到的性能度量都在[0, 1]之间,可以判断此模型更适合预测哪个问题。
三、Python代码实现
暂时空着,实践整理后完善 ~~~