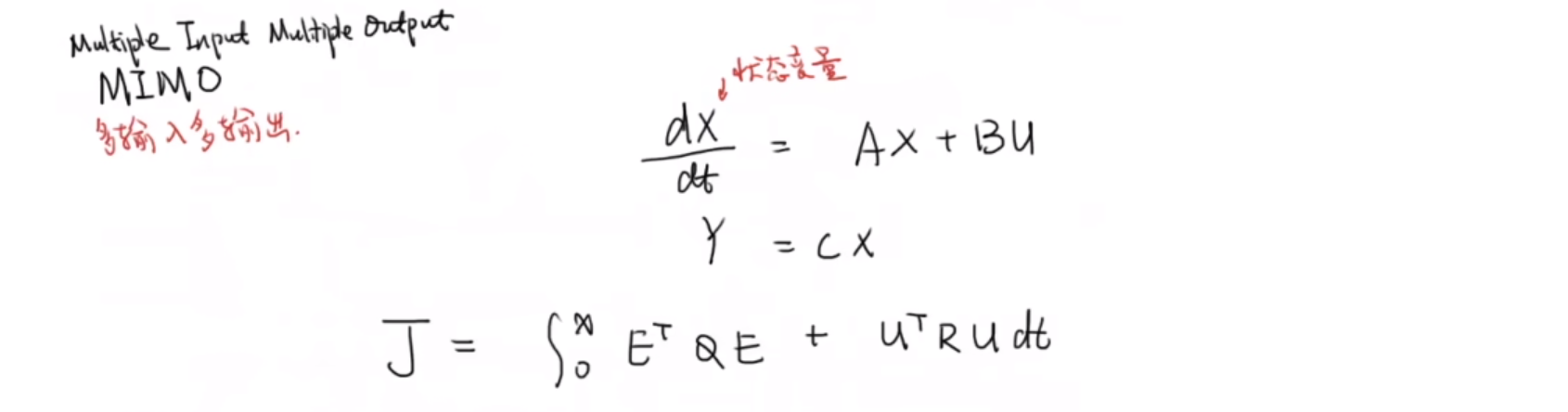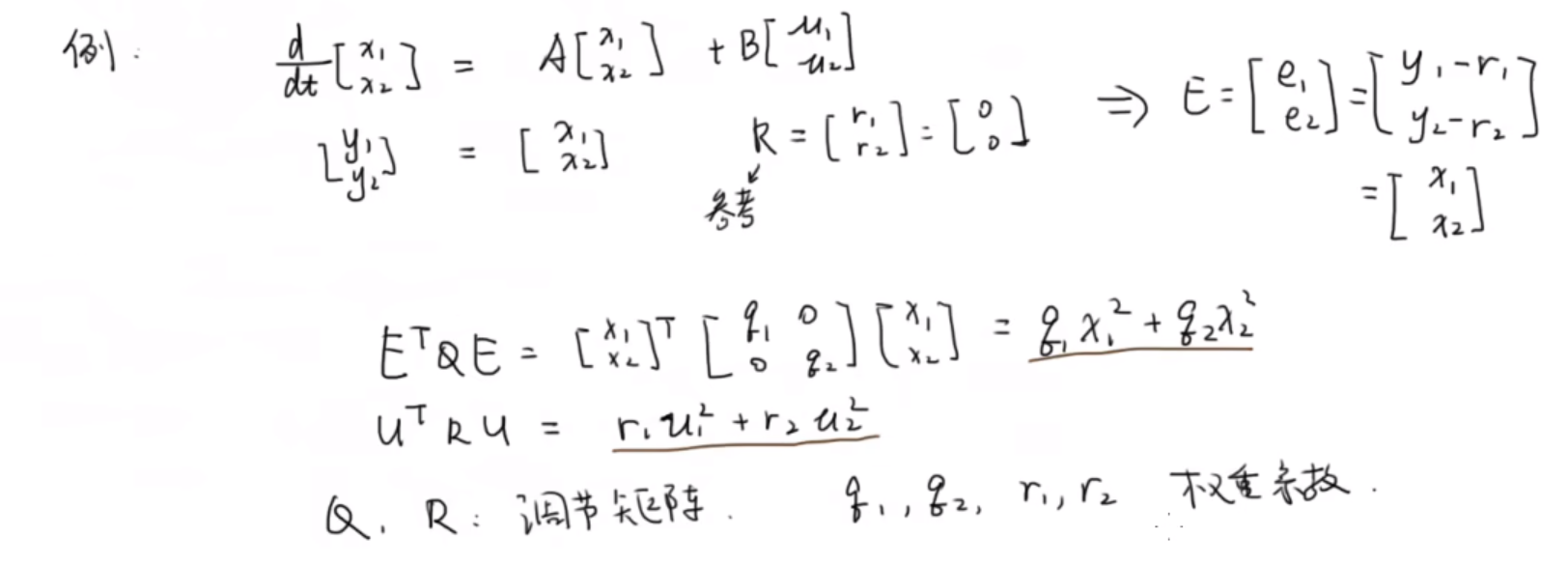MPC模型预测控制器学习笔记（附程序）

本文用于记录学习DR_CAN老师发布的MPC系列视频教程的相关内容，文章中放的源码也是DR_CAN老师提供的程序示例，链接如下：

一、最优化控制与MPC基本概念

1、最优化控制基本概念

最优控制的研究动机是在约束条件下（如物理限制）达到最优（综合性最优）的系统表现，在轨迹追踪中可以用真实值与期望值的差值e的平方的积分 $\int_0^te^2dt$ 来表征追踪效果,其值越小，跟踪效果越好。可以用输入u的平方的积分 $\int_0^tu^2dt$ 来表征所需输入的大小

在这里插入图片描述

我们可以构造目标/代价函数为 $J=\int_{0}^{t}qe^{2}+ru^{2}dt$ ，最优化过程就是设计一个控制器u使得 $J$ 达到最小值，q和r是可以调节的参数。若设置的q远大于r，则说明在优化过程中更看重误差e的大小。同理，若r远大于q，则更看重输入

在这里插入图片描述

对于多输入多输出的MIMO系统可以用状态空间方程进行表示 $\frac{dx}{dt}=\quad Ax+Bu$ 、 $Y = c x$ ，x是系统状态变量，Y是系统输出。其目标函数为 $J=\int_{0}^{x}E^{T}Q E+u^{T}Rudt$

在这里插入图片描述

看一个例子，假如我们有一个如下式所示的二维系统，参考值选为[0 0 $^T$

$\begin{aligned}&\frac d{dt}\left[\begin{array}{c}x_1\\x_1\end{array}\right]\quad=\quad A\left[\begin{array}{c}x_1\\x_2\end{array}\right]+B\left[\begin{array}{c}\mu_1\\\mu_2\end{array}\right]\\\\&\begin{bmatrix}y_1\\y_2\end{bmatrix}=\quad\left[\begin{array}{c}x_1\\x_2\end{array}\right]\end{aligned}.$

则 $E=[x_1 \quad x_2]^T$ ， $E^TQE$ 和 $U^TRU$ 的表达式如下图所示，其中Q和R是调节矩阵，其中的q1、q2、r1、r2就是我们可以调节的权重系数，若我们只关心 $x_1$ 的追踪情况，就把q1设置的比较大，q2设置的比较小或0，这里就不会关注 $x_2$ 的追踪情况了

在这里插入图片描述

2、MPC基本概念

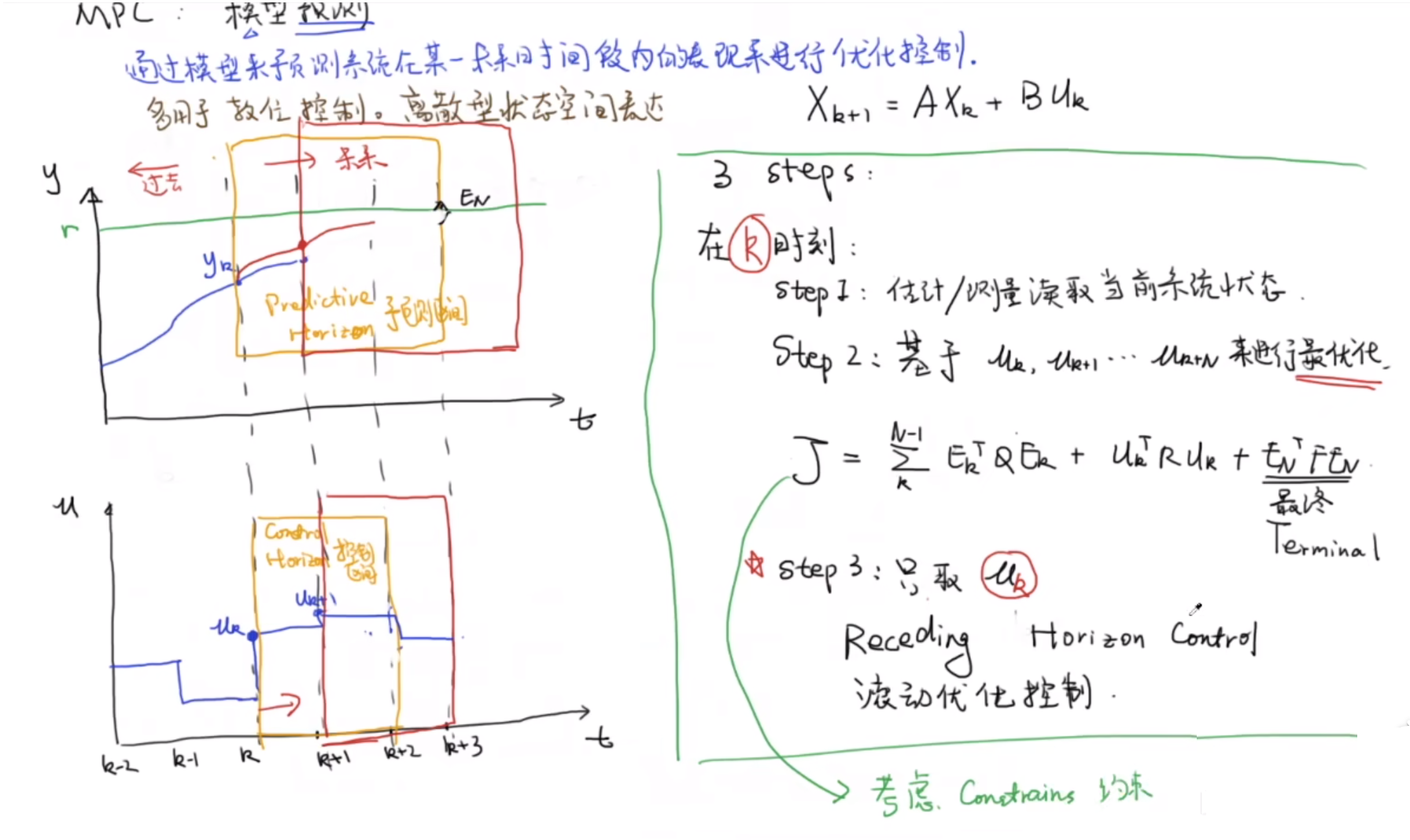
简单来说，MPC就是通过模型来预测系统在某一未来时间段内的表现来进行优化控制，多用于数位控制，所以分析时常采用离散型的状态空间表达形式 $X_{k+1}=AX_{k}+BU_{k}$

在这里插入图片描述

MPC的设计和实施包含三个步骤，在k时刻第一步要做的是，估计/测量出系统当前状态。

第二步是基于 $u_{k}$ 、 $u_{k+1}$ 、 $u_{k+2}$ 、 $u_{k+3}$ … $u_{k+n}$ 来做最优化控制，即在k时刻施加一个输入 $u_{k}$ ，根据我们的模型来预测系统k ~ k+1时间段内的表现，然后基于预测的k+1时刻的表现，再施加一个输入 $u_{k+1}$ 、再根据我们的模型来预测系统k+1 ~ k+2时间段内的表现，以此类推，直至预测完我们设定的预测区间，比如k~k+3时间段。则输入 $u_{k}$ 、 $u_{k+1}$ 、 $u_{k+2}$ 称为控制区间，在这个控制区间， $u_{k}$ 、 $u_{k+1}$ 、 $u_{k+2}$ 的选择就是一个最优化的问题。来使得下式所示的目标函数最小，其中，最后一项 $E_{N}^{T}FE_{N}$ 表示预测区间的最后一个时刻，与期望值误差的惩罚项

$J=\sum_{k}^{N-1}E_{k}^{T}QE_{k}+U_{k}^{T}RU_{k}+E_{N}^{T}FE_{N}$

第三步是非常重要的一步，也是MPC当中非常有技巧性的一步，通过上面的计算。我们其实得到了 $u_{k}$ 、 $u_{k+1}$ 、 $u_{k+2}$ 这三个输入，但是在实施的时候，并不是把这三个数值输入都实施下去，而是在K时刻只实施 $u_{k}$ 这一个在k时刻计算出来的最优化结果。
在这里插入图片描述

在实施的时候只取 $u_{k}$ 这一个输入非常非常的重要，这是因为我们预测的模型很难完美的描述现实的系统，而且，在现实的系统当中可能会有扰动，就是说我们预测出来的实施 $u_{k}$ 后，它的输出 $Y_{k}$ 与现实当中真正执行完 $u_{k}$ 后的 $Y_{k}$ 是有偏差的，这就要求当我们实施 $u_{k}$ 之后，在k+1时刻要把上面的三步重新执行一遍，即把整个的预测区间(control horizon)和控制区间(predictive horizon)向右移动一个时刻。这个过程就称为滚动优化控制(receiving horizon control)。

可以看得出来这样的一个解决方案，它在每一步的时候都要进行一下最优化的一个计算。所以MPC对控制器的计算能力要求是很高的。另外一个MPC的特点就是在他求解这个最优化问题的时候，他会考虑到系统的约束。

二、最优化数学建模与推导

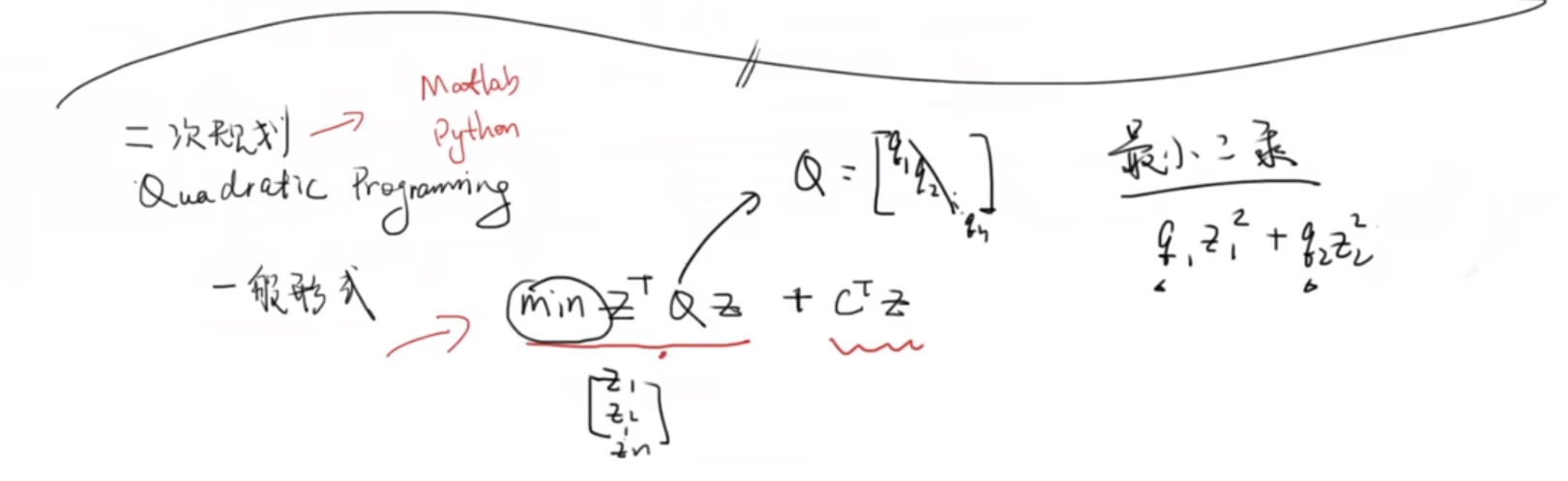
在这里插入图片描述

MPC算法的重点在第二步，即最优化部分，方法有很多种，这里介绍二次规划QP方法

在这里插入图片描述

下面来看一下，如何建立二次规划的模型，其中 $u (k + 1∣ k)$ 表示的是在k时刻，对k+1时刻的输入的预测，一直预测到k+N-1时刻，N叫做预测空间，同理 $x (k + 1∣ k)$ 表示k时刻对k+1时刻状态的预测，一直预测到k+N时刻，

在这里插入图片描述

我们依然假设y=x，参考值为0，目标函数依然由误差加权和、输入加权和、终端误差三部分构成，如下所示：

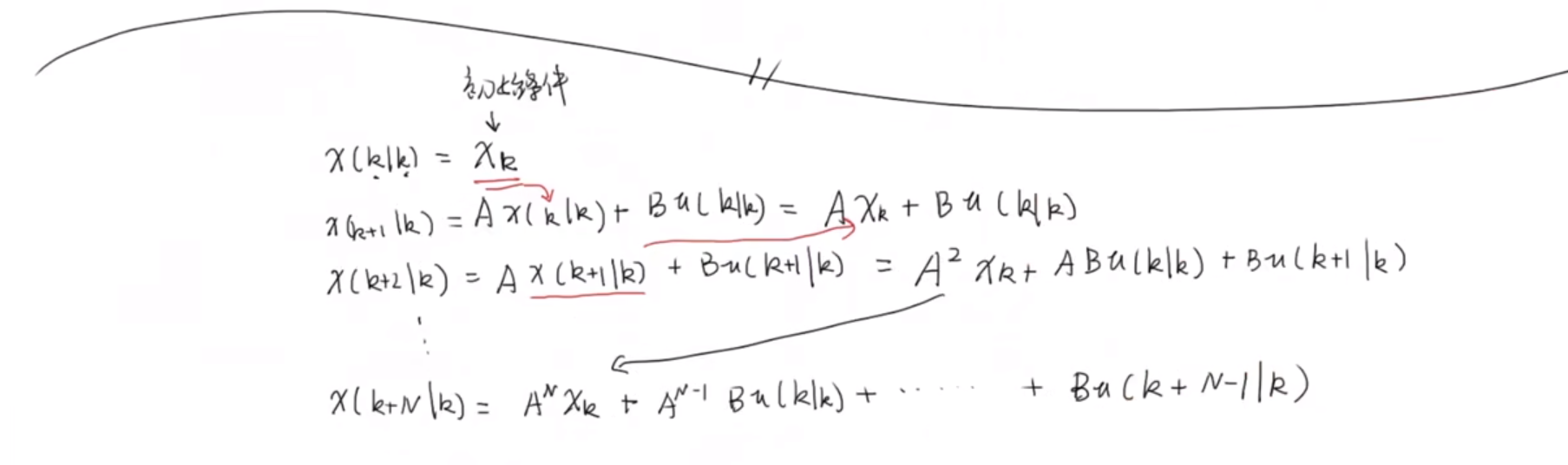
在这里插入图片描述

上面的目标函数中含有未知量x和u，由于我们是要对u进行优化，所以需要把x消去，假设在k时刻对k时刻状态量的预测 $x (k ∣ k)$ 为 $x_{k}$ ，则k时刻对k+1时刻状态量的预测 $x (k + 1∣ k)$ 可利用状态方程进行化简推导… 然后，我们就可以推导出 $x (k + N ∣ k)$ 的表达式。

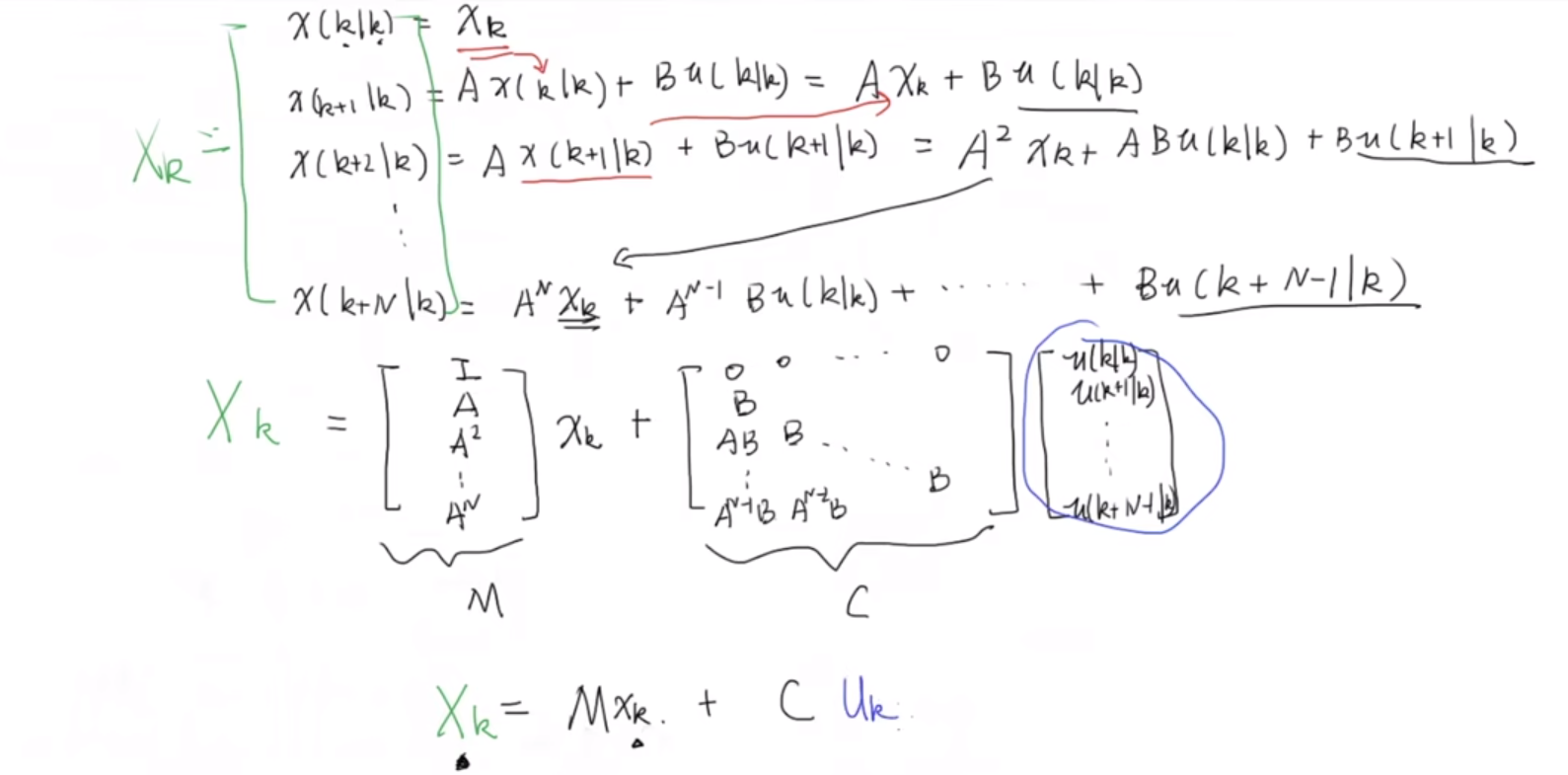
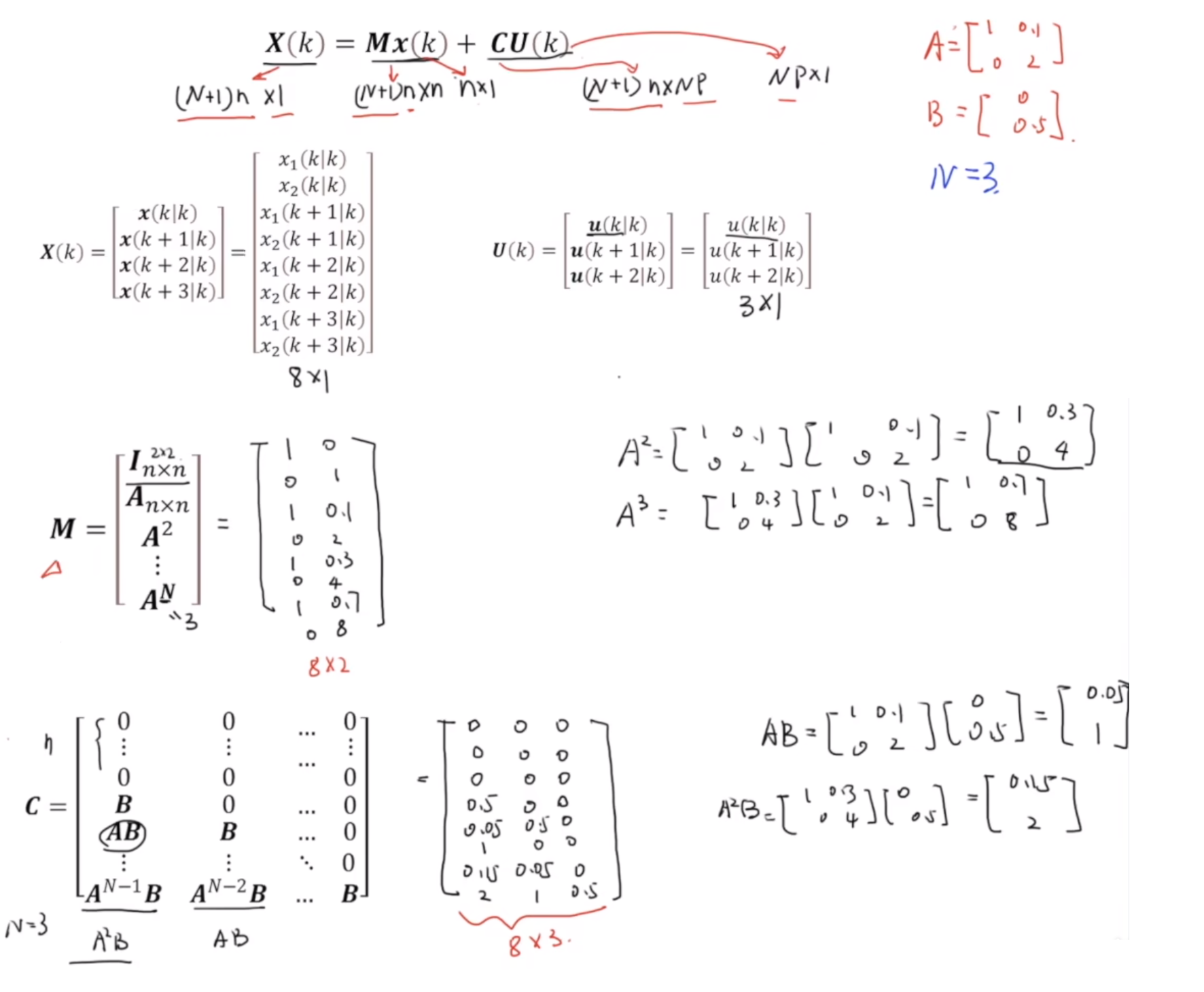
在这里插入图片描述

我们可以利用前面介绍的矩阵形式的 $X_k$ 和 $U_K$ 将其表示成更加简洁的形式 $X_{k}=Mx_{k}+CU_{k}$

在这里插入图片描述

我们再来看一下目标\代价函数，将其展开，并整理，也写成用矩阵 $X_k$ 和 $U_K$ 表示的形式 $J=X_{k}^{T}\bar{Q}X_{k}+U_{k}^{T}\bar{R}U_{k}^{}$

在这里插入图片描述

然后将前面推出的 $X_{k}=Mx_{k}+CU_{k}$ 代入到 $J=X_{k}^{T}\bar{Q}X_{k}+U_{k}^{T}\bar{R}U_{k}^{}$ 中就可以消去 $X_{k}$

在这里插入图片描述

最终得到目标函数的表达式如下，其中 $x_{k}$ 给定的初始状态，是测量值。

$J=x_{k}^{T}Gx_{k}+2x_{k}^{T}EU_{k}+U_{k}^{T}HU_{k}$

三、一个详细的建模例子

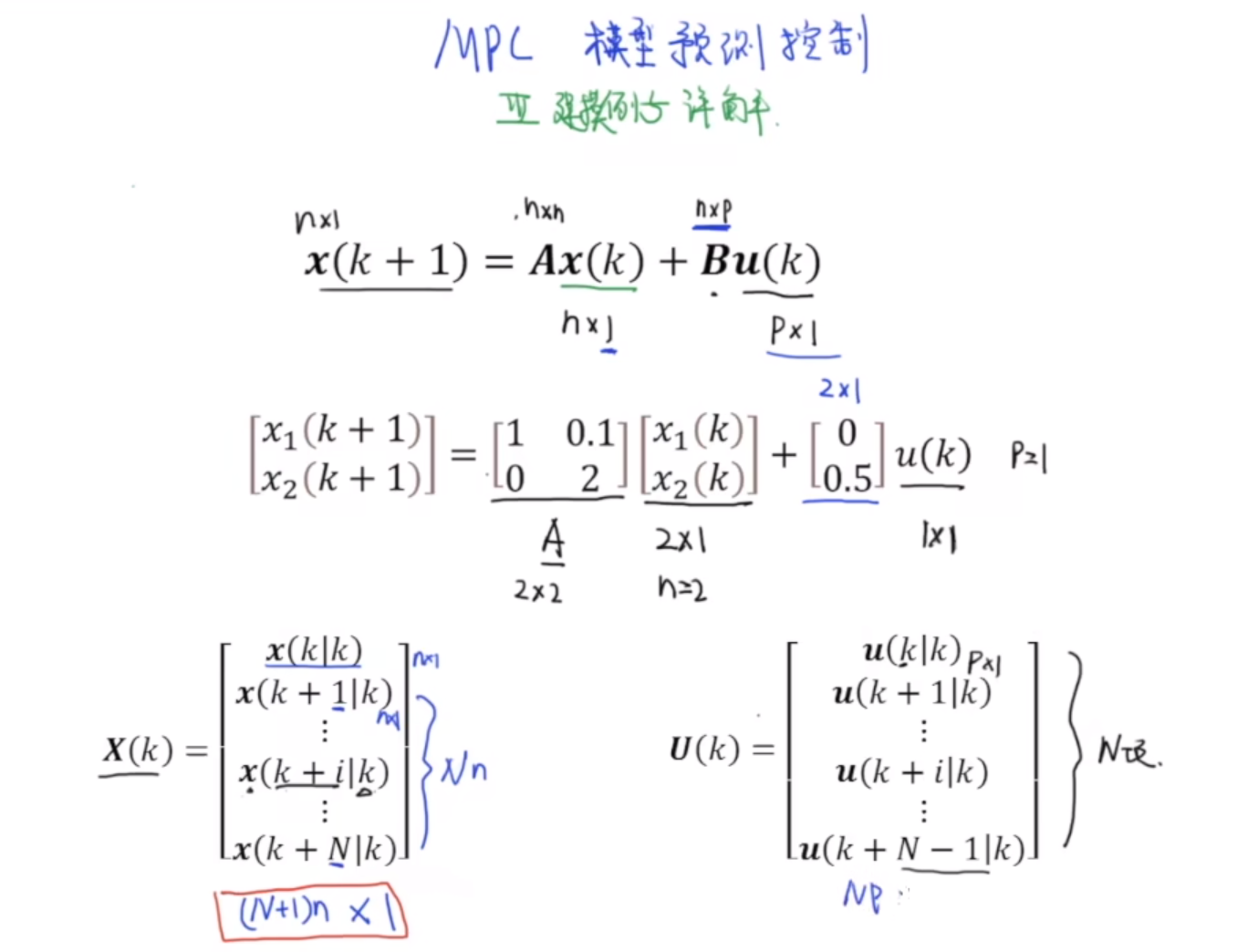
在这里插入图片描述

下面，我们以 $A=\begin{bmatrix}1&0.1\\0&2\end{bmatrix}$ , $B=\begin{bmatrix}0\\0.5\end{bmatrix}$ 为例，假设预测空间N=3，进行具体的计算。

在这里插入图片描述

如果，我们的目标是让x趋于0，则代价函数可以表示成如下的形式，Q、R、F分别表示权重系数矩阵

$J=\sum_{i=0}^{N-1}(x(k+i|k)^{T}Qx(k+i|k)+u(k+i|k)^{T}Ru(k+i|k))+x(k+N|k)^{T}Fx(k+N|k)$

通过前面的介绍，我们可以对上式进行简化，简化后的表达式如下,除了系数矩阵，它只包含了输入项和初始状态，初始状态又是给定已知的，所以，未知项，也即需要优化的项为输入项 $U (k)$

$J=\boldsymbol{x}(k)^T\boldsymbol{G}\dot{\boldsymbol{x}}(k)+\boldsymbol{U}(k)^T\boldsymbol{H}\boldsymbol{U}(k)+2\boldsymbol{x}(k)^T\boldsymbol{E}\boldsymbol{U}(k)$

其中，上式中的系数矩阵的表达式如下：

$\begin{aligned}G&=M^T\overline{Q}M\\\\E&=C^T\overline{Q}M\\\\H&=C^T\overline{Q}C+\overline{R}\end{aligned}.$

其中， $\overline{Q}$ 和 $\overline{R}$ 是前面两个系数矩阵的增广形式，如下所示：

$\overline{Q}=\begin{bmatrix}Q&\cdots&\\\vdots&Q&\vdots\\&\cdots&F\end{bmatrix}\quad\overline{R}=\begin{bmatrix}R&\cdots&\\\vdots&\ddots&\vdots\\&\cdots&R\end{bmatrix}$

四、完整案例及程序讲解

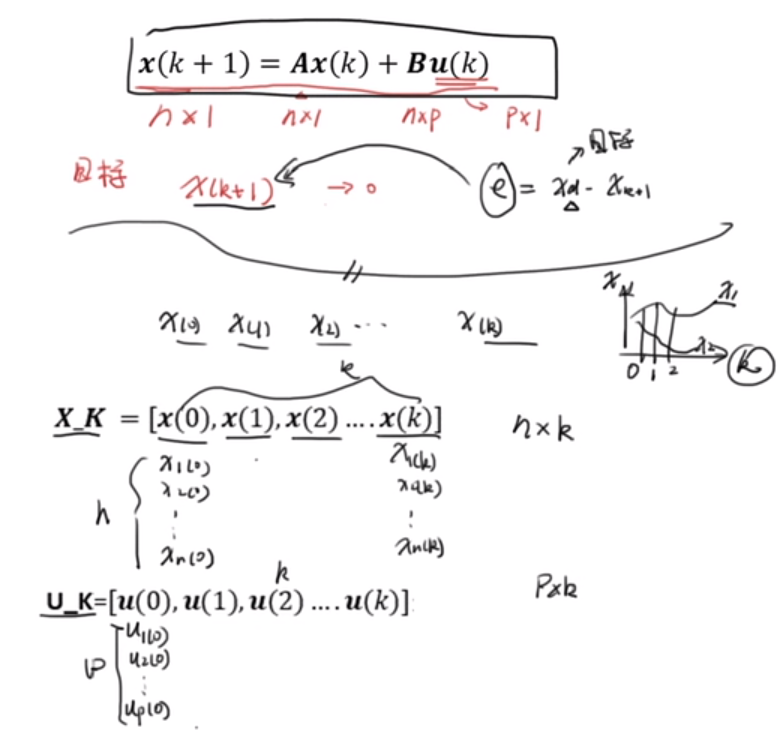
研究对象是离散形式的状态空间方程，目标是设计合适的 $U_k$ ，使得系统的状态变量 $x (k)$ 随着k的增加趋近于目标值，引入误差这个概念，它等于状态量的期望值减去实际值，即e= $x_d-x_{k+1}$ ，这样的话，我们的目标就是要让这个误差量趋向于0。

为了方便观察，我们会需要把系统的状态变量x随着k的增加的变化趋势画出来，横坐标是k，纵坐标是x值。因此我们需要建立两个新的矩阵X_K和U_K，分别累计存放每个k所对应的状态量和输入量

在这里插入图片描述

定义了这两个矩阵后，在MATLAB或者Octave中状态方程就可以写成如下的形式：

$X\_K(:,k+1)=(A^{*}X\_K(:,k)+B^{*}U\_K(:,k));$

接着看前面给出的具体例子，即取 $A=\begin{bmatrix}1&0.1\\0&2\end{bmatrix}$ , $B=\begin{bmatrix}0\\0.5\end{bmatrix}$ ，状态变量的权重矩阵Q、状态变量终端的权重（终端惩罚）矩阵F、输入的权重矩阵R的取值如下：

$\boldsymbol{Q}=\begin{pmatrix}1&0\\0&1\end{pmatrix}\quad\boldsymbol{F}=\begin{pmatrix}1&0\\0&1\end{pmatrix}\boldsymbol{R}=0.1$

由前面的介绍可知，目标函数表达式如下：优化变量

$J=\boldsymbol{x}(k)^T\boldsymbol{G}\dot{\boldsymbol{x}}(k)+\boldsymbol{U}(k)^T\boldsymbol{H}\boldsymbol{U}(k)+2\boldsymbol{x}(k)^T\boldsymbol{E}\boldsymbol{U}(k)$

可知第一部分与优化变量 $U (k)$ 没有关系，所以优化时只需要最设计合适的 $U (k)$ 来最小化下式即可

$\boldsymbol{U}(k)^T\boldsymbol{H}\boldsymbol{U}(k)+2\boldsymbol{x}(k)^T\boldsymbol{E}\boldsymbol{U}(k)$

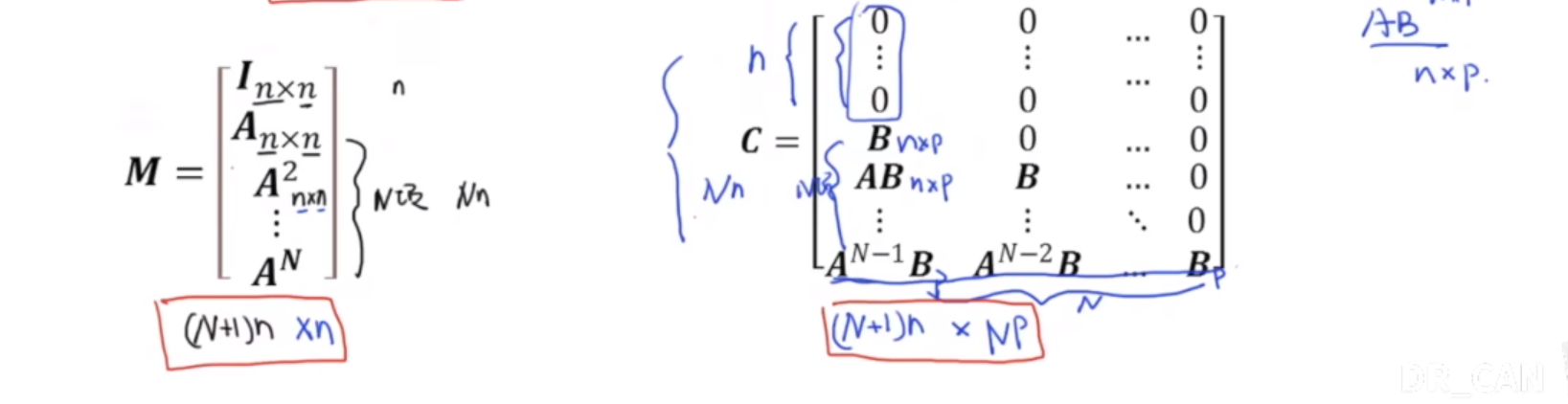
其中，矩阵H和E的表达式如下：

$\begin{array}{l}{E=C^{T}\overline{Q}M}\\{H=C^{T}\overline{Q}C+\overline{R}}\\\end{array}$

$\begin{aligned}&\boldsymbol{C}=\begin{bmatrix}0&0&\ldots&0\\\vdots&\vdots&\ldots&\vdots\\0&0&\ldots&0\\\boldsymbol{B}&0&\ldots&0\\\boldsymbol{AB}&\boldsymbol{B}&\ldots&0\\\varvdots&\varvdots&\ddots&0\\\boldsymbol{A}^{N-1}\boldsymbol{B}&\boldsymbol{A}^{N-2}\boldsymbol{B}&\ldots&\boldsymbol{B}\end{bmatrix}\boldsymbol{M}=\begin{bmatrix}\boldsymbol{I}_{n\times n}\\\boldsymbol{A}_{n\times n}\\\boldsymbol{A}^2\\\boldsymbol{A}^N\end{bmatrix}\\&\vec{Q}=\begin{bmatrix}\boldsymbol{Q}&\cdots\\\varvdots&\boldsymbol{Q}&\vdots\\&\cdots&\boldsymbol{F}\end{bmatrix}\quad\vec{R}=\begin{bmatrix}\boldsymbol{R}&\cdots&\\\varvdots&\ddots&\vdots\\&\cdots&\boldsymbol{R}\end{bmatrix}\end{aligned}$

在编程实现上：

①、首先设定矩阵A、B、Q、F、R，设定k的最大值，给定初始状态x，并初始化X_K和U_K矩阵，设定预测区间N

②、然后根据表达式计算系数矩阵G、E、H

③、开始循环迭代，在每次迭代中，提供当前状态 $x_k$ 、矩阵E、H，预测区间N，然后使用优化算法（本例中调用的MATLAB自带的最优化函数quadprog）计算输入 $U_k$ , 并使用状态方程对 $X_k$ 进行更新

④、图像绘制

DR_CAN老师给出的代码一共由三个部分组成，分别为主程序： MPC_Test.m。以及两个函数： MPC_Matrices.m 和 Prediction.m。代码使用Octave编写，同时也在Matlab中经过了验证。

（1）、MPC_Test.m

%% 清屏

clear ; 

close all; 

clc;

%% 加载 optim package,若使用matlab，则注释掉此行

pkg load optim;

%%%%%%%%%%%%%%%%%%%%%%%%%%

%% 第一步，定义状态空间矩阵

%% 定义状态矩阵 A, n x n 矩阵

A = [1 0.1; -1 2];

n= size (A,1);

%% 定义输入矩阵 B, n x p 矩阵

B = [ 0.2 1; 0.5 2];

p = size(B,2);

%% 定义Q矩阵，n x n 矩阵

Q=[100 0;0 1];

%% 定义F矩阵，n x n 矩阵

F=[100 0;0 1];

%% 定义R矩阵，p x p 矩阵

R=[1 0 ;0 .1];

%% 定义step数量k

k_steps=100; 

%% 定义矩阵 X_K， n x k 矩 阵

X_K = zeros(n,k_steps);

%% 初始状态变量值， n x 1 向量

X_K(:,1) =[20;-20];

%% 定义输入矩阵 U_K， p x k 矩阵

U_K=zeros(p,k_steps);



%% 定义预测区间K

N=5;

%% Call MPC_Matrices 函数 求得 E,H矩阵 

[E,H]=MPC_Matrices(A,B,Q,R,F,N);



%% 计算每一步的状态变量的值

for k = 1 : k_steps 

%% 求得U_K(:,k)

U_K(:,k) = Prediction(X_K(:,k),E,H,N,p);

%% 计算第k+1步时状态变量的值

X_K(:,k+1)=(A*X_K(:,k)+B*U_K(:,k));

end



%% 绘制状态变量和输入的变化

subplot  (2, 1, 1);

hold;

for i =1 :size (X_K,1)

plot (X_K(i,:));

end

legend("x1","x2")

hold off;

subplot (2, 1, 2);

hold;

for i =1 : size (U_K,1)

plot (U_K(i,:));

end

legend("u1","u2")

（2）、MPC_Matrices.m

function  [E , H]=MPC_Matrices(A,B,Q,R,F,N)


n=size(A,1);   % A 是 n x n 矩阵, 得到 n

p=size(B,2);   % B 是 n x p 矩阵, 得到 p

%%%%%%%%%%%%

M=[eye(n);zeros(N*n,n)]; % 初始化 M 矩阵. M 矩阵是 (N+1)n x n的， 

                         % 它上面是 n x n 个 "I", 这一步先把下半部

                         % 分写成 0 

C=zeros((N+1)*n,N*p); % 初始化 C 矩阵, 这一步令它有 (N+1)n x NP 个 0

% 定义M 和 C 

tmp=eye(n);  %定义一个n x n 的 I 矩阵

%　更新Ｍ和C

for i=1:N % 循环，i 从 1到 N

    rows =i*n+(1:n); %定义当前行数，从i x n开始，共n行 

    C(rows,:)=[tmp*B,C(rows-n, 1:end-p)]; %将c矩阵填满

    tmp= A*tmp; %每一次将tmp左乘一次A

    M(rows,:)=tmp; %将M矩阵写满

end 


% 定义Q_bar和R_bar

Q_bar = kron(eye(N),Q);

Q_bar = blkdiag(Q_bar,F);

R_bar = kron(eye(N),R); 



% 计算G, E, H

G=M'*Q_bar*M; % G: n x n

E=C'*Q_bar*M; % E: NP x n

H=C'*Q_bar*C+R_bar; % NP x NP 



end

（3）、Prediction.m

function u_k= Prediction(x_k,E,H,N,p)

U_k = zeros(N*p,1); % NP x 1

U_k = quadprog(H,E*x_k);

u_k = U_k(1:p,1); % 取第一个结果

end

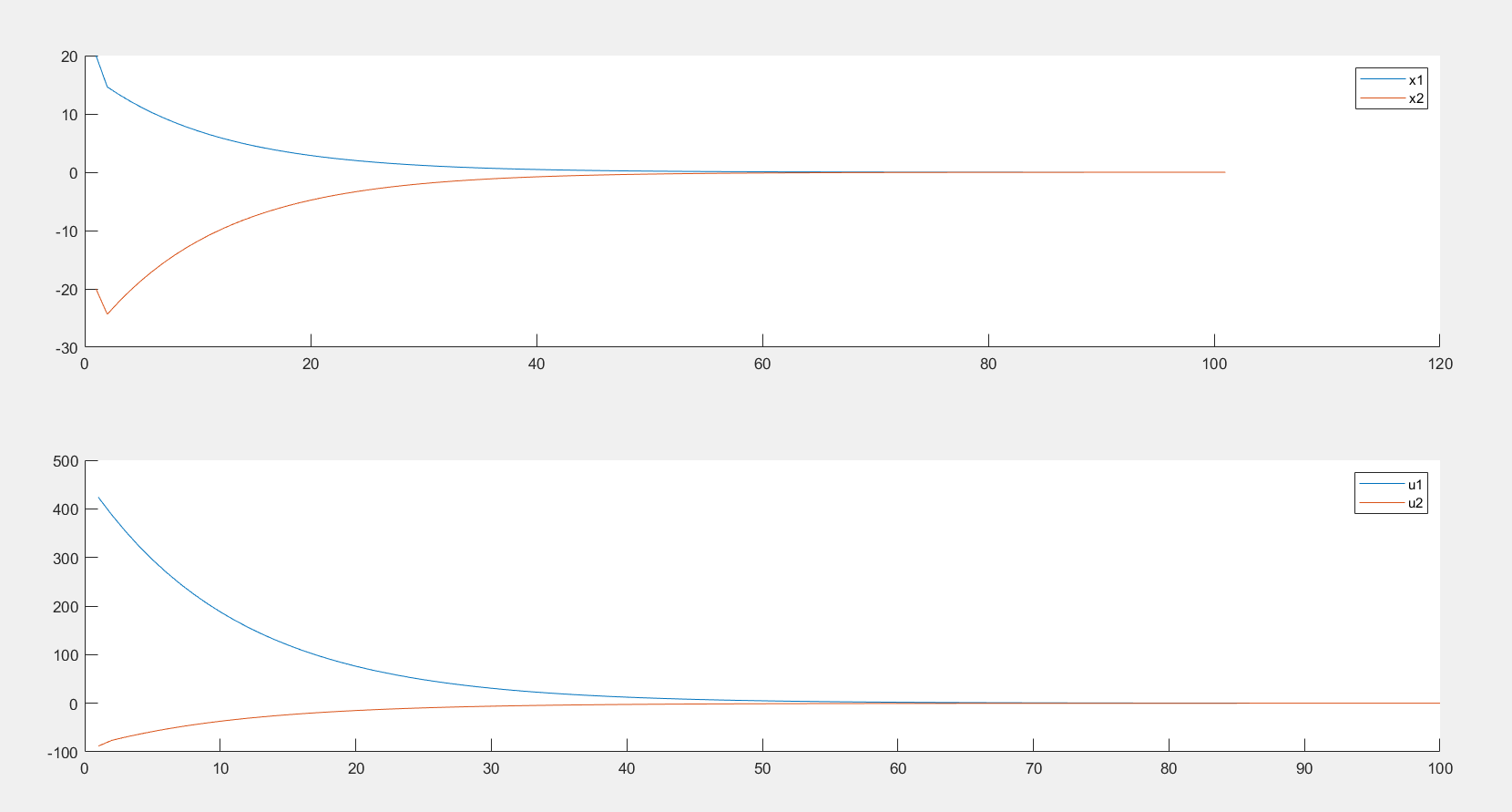
程序运行结果如下：

在这里插入图片描述

参考资料

1、DR_CAN老师的视频教程链接（点击可跳转）

2、DR_CAN老师提供的程序示例（点击可跳转）

MPC模型预测控制器学习笔记（附程序）

悦读