运动学建模、线性化、离散化过程,是使用控制算法进行控制前常用的操作,本文主要以车辆/单车模型为例,详细介绍运动学建模、线性化、离散化等过程,为后续的使用LQR、MPC等控制算法进行轨迹跟踪或其他控制任务做准备。
一、车辆/单车 运动学建模
设机器人当前的位姿为 ( x c , y c , φ c ) (x_c, y_c, φ_c) (xc,yc,φc), 其中 ( x c , y c , ) (x_c, y_c,) (xc,yc,) 为其当前位置坐标, φ c φ_c φc为其当前姿态角,当前前轮的转向角为 δ c δ_c δc,当前的后轮车速为 v c v_c vc,前轮车速为 v f v_f vf,前后轮距为 l l l,默认采用后轮驱动模式,即可控的是后轮车速 v c v_c vc,如下图所示:
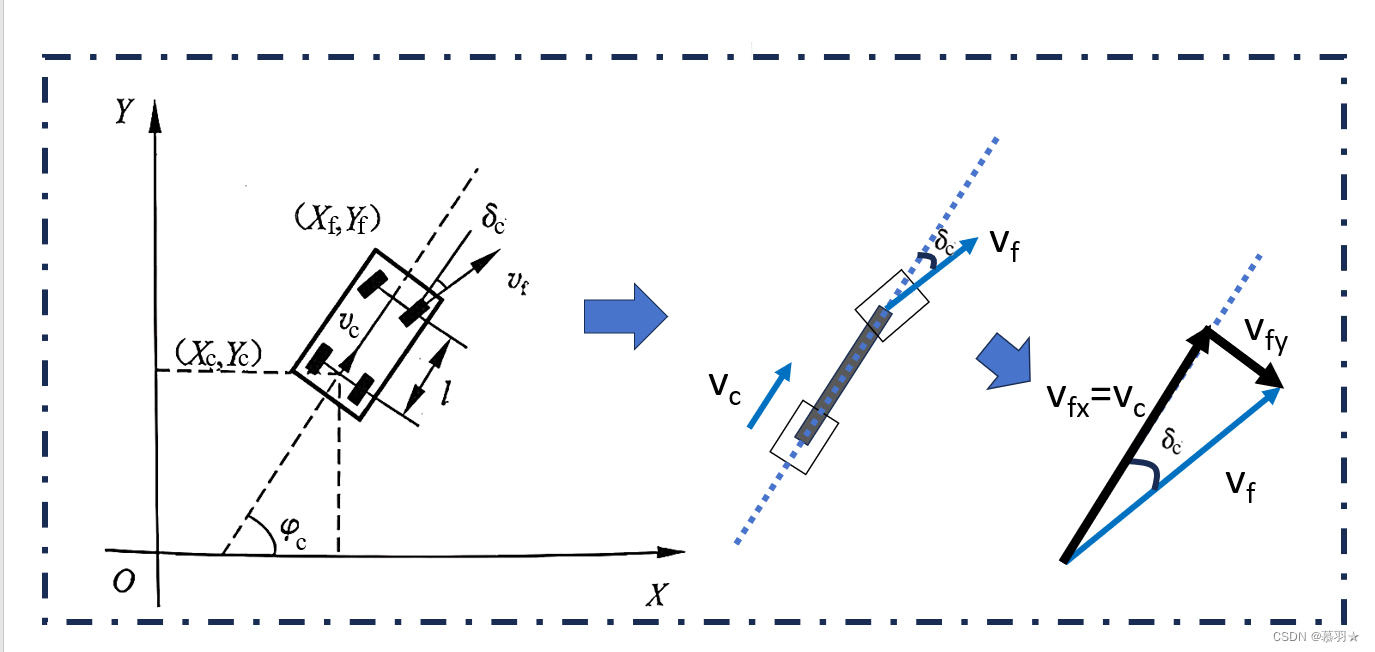
容易得到 v c v_c vc在x轴和y轴的的分量为别为 v c c o s ( φ c ) v_ccos(φ_c) vccos(φc)、 v c s i n ( φ c ) v_csin(φ_c) vcsin(φc),即:
x c ˙ = v c c o s ( φ c ) y c ˙ = v c s i n ( φ c ) \dot{x_c}=v_ccos(φ_c) \\ \dot{y_c}=v_csin(φ_c) xc˙=vccos(φc)yc˙=vcsin(φc)
刚体在同一方向上的速度是相同的,即前轮车速在车辆当前移动方向 v c v_c vc上的分量应该与 v c v_c vc相同,即 v f x = v c v_{fx}=v_c vfx=vc,这个分量与车辆运行方向相同,对车辆的转向无作用,导致车辆运行方向改变的是分量 v f y = v c t a n ( δ c ) v_{fy}=v_ctan(δ_c) vfy=vctan(δc),将其视为车辆绕后轮旋转的线速度,除以半径 l l l,即为旋转角速度,如下所示:
φ c ˙ = v c t a n ( δ c ) l \dot{φ_c}=\frac{v_ctan(δ_c)}{l} φc˙=lvctan(δc)
所以,我们可以得到完整的单车运动学模型的状态空间表达式如下:
{ x c ˙ = v c c o s ( φ c ) y c ˙ = v c s i n ( φ c ) φ c ˙ = v c t a n ( δ c ) l \begin{cases}\dot{x_c}=v_ccos(\varphi_c)\\\dot{y_c}=v_csin(\varphi_c)\\\dot{\varphi_c}=\frac{v_ctan(\delta_c)}l\end{cases} ⎩ ⎨ ⎧xc˙=vccos(φc)yc˙=vcsin(φc)φc˙=lvctan(δc)
二、将状态空间表达式线性化
第一部分中得到了运动学建模的状态空间表达式,然而它是非线性的,想要用来做控制,需要将其化为线性的,先将其写成向量的形式 ,取状态量 X c = [ x c y c φ c ] T X_c=[x_c\ y_c\ φ_c]^T Xc=[xc yc φc]T,控制输入为 u = [ v c δ c ] T u=[v_c \ δ_c]^T u=[vc δc]T, 即前轮转向,后轮驱动。则向量形式的状态空间可写为(因为是非线性的,不能写成矩阵形式):
X ˙ = f ( X , u ) \dot{X}=f(X,u) X˙=f(X,u)
最常用的近似线性化方法就是泰勒展开,在 x 0 x_0 x0点处展开的泰勒展开式如下所示:
f ( x ) = f ( x 0 ) 0 ! + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + . . . + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + R n ( x ) f\left(x\right)=\frac{f\left(x_{0}\right)}{0!}+\frac{f'\left(x_{0}\right)}{1!}\left(x-x_{0}\right)+\frac{f''\left(x_{0}\right)}{2!}\left(x-x_{0}\right)^{2}+...+\frac{f^{\left(n\right)}\left(x_{0}\right)}{n!}\left(x-x_{0}\right)^{n}+R_{n}(x) f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!f(n)(x0)(x−x0)n+Rn(x)
使用泰勒展开进行线性化需要选择一个展开点,前面我们已经设定了当前位姿(状态)为 ( x c , y c , φ c ) (x_c, y_c, φ_c) (xc,yc,φc),现在补充设定目标位姿(状态)为 ( x r , y r , φ r ) (x_r, y_r, φ_r) (xr,yr,φr),将目标位姿作为展开点,对 f ( X , u ) f(X,u) f(X,u)进行泰勒展开,展开到一阶线性项,如下所示:
X ˙ ≈ f ( X r , u r ) + ∂ f ( X r , u r ) ∂ X r ( X − X r ) + ∂ f ( X r , u r ) ∂ u r ( u − u r ) \dot{X}\approx f(X_{r},u_{r})+\frac{\partial f(X_r,u_r)}{\partial X_r}(X-X_{r})+\frac{\partial f(X_r,u_r)}{\partial u_r}(u-u_{r}) X˙≈f(Xr,ur)+∂Xr∂f(Xr,ur)(X−Xr)+∂ur∂f(Xr,ur)(u−ur)
即:
X ˙ − X r ˙ ≈ ∂ f ( X r , u r ) ∂ X r ( X − X r ) + ∂ f ( X r , u r ) ∂ u r ( u − u r ) \dot{X}-\dot{X_r}\approx \frac{\partial f(X_r,u_r)}{\partial X_r}(X-X_{r})+\frac{\partial f(X_r,u_r)}{\partial u_r}(u-u_{r}) X˙−Xr˙≈∂Xr∂f(Xr,ur)(X−Xr)+∂ur∂f(Xr,ur)(u−ur)
这里的线性化,并不是把非线性关系,转换为线性关系,而是通过展开,使其误差变为一个线性关系,如上式所示,展开后的误差是线性的, 所以我们可以取当前量与目标量(参考量)之间的差值为新的状态量和输入项,如下所示:
X ~ ˙ = [ x c ˙ − x ˙ r y c ˙ − y ˙ r φ c ˙ − φ ˙ r ] , X ~ = [ x c − x r y c − y r φ c − φ r ] , u ~ = [ v c − v r δ c − δ r ] \dot{\tilde{X}}=\begin{bmatrix}\dot{x_c}-\dot{x}_{r}\\ \dot{y_c}-\dot{y}_{r}\\ \dot{\varphi_c}-\dot{\varphi}_{r}\end{bmatrix},{\tilde{X}}=\begin{bmatrix}{x_{c}}-x_{r}\\ {y_c}-{y}_{r}\\ {\varphi_c}-{\varphi}_{r}\end{bmatrix},\mathbf{\tilde{u}}=\begin{bmatrix}v_{c}-v_{r}\\ \delta_{c}-\delta_{r}\end{bmatrix} X~˙= xc˙−x˙ryc˙−y˙rφc˙−φ˙r ,X~= xc−xryc−yrφc−φr ,u~=[vc−vrδc−δr]
则上面得到的展开式可以写为:
X ~ ˙ ≈ ∂ f ( X r , u r ) ∂ X r X ~ + ∂ f ( X r , u r ) ∂ u r u ~ \dot{\tilde{X}}\approx \frac{\partial f(X_r,u_r)}{\partial X_r}{\tilde{X}}+\frac{\partial f(X_r,u_r)}{\partial u_r}{\tilde{u}} X~˙≈∂Xr∂f(Xr,ur)X~+∂ur∂f(Xr,ur)u~
也就是我们常见的 X ˙ = A X + B u \dot{{X}}= A{{X}}+B{{u}} X˙=AX+Bu的状态空间表达式的形式,成功完成了线性化,求矩阵A和B,也就是 ∂ f ( X r , u r ) ∂ X r \frac{\partial f(X_r,u_r)}{\partial X_r} ∂Xr∂f(Xr,ur)和 ∂ f ( X r , u r ) ∂ u r \frac{\partial f(X_r,u_r)}{\partial u_r} ∂ur∂f(Xr,ur)实际上,也就是在求雅克比矩阵,如下所示:
注:下式中的 f f f是 f ( X r , u r ) f(X_r,u_r) f(Xr,ur)的简称
{ f 1 = v r c o s ( φ r ) f 2 = v r s i n ( φ r ) f 3 = v r t a n ( δ r ) l \begin{cases}{f_1}=v_rcos(\varphi_r)\\{f_2}=v_rsin(\varphi_r)\\{f_3}=\frac{v_rtan(\delta_r)}l\end{cases} ⎩ ⎨ ⎧f1=vrcos(φr)f2=vrsin(φr)f3=lvrtan(δr)
A = ∂ f ( X r , u r ) ∂ X r = [ ∂ f 1 ∂ x r ∂ f 1 ∂ y r ∂ f 1 ∂ φ r ∂ f 2 ∂ x r ∂ f 2 ∂ y r ∂ f 2 ∂ φ r ∂ f 3 ∂ x r ∂ f 3 ∂ y r ∂ f 3 ∂ φ r ] = [ 0 0 − v r sin φ r 0 0 v r cos φ r 0 0 0 ] A=\frac{\partial f\left(X_{r},u_r\right)}{\partial X_r}=\begin{bmatrix}\frac{\partial f_1}{\partial x_{r}} & \frac{\partial f_1}{\partial y_{r}} & \frac{\partial f_1}{\partial\varphi_{r}}\\ \frac{\partial f_2}{\partial x_{r}} & \frac{\partial f_2}{\partial y_{r}} & \frac{\partial f_2}{\partial\varphi_{r}}\\ \frac{\partial f_3}{\partial x_{r}} & \frac{\partial f_3}{\partial y_{r}} & \frac{\partial f_3}{\partial\varphi_{r}}\end{bmatrix}=\begin{bmatrix}0 & 0 & -v_r\sin\varphi_{r}\\ 0 & 0 & v_r\cos\varphi_{r}\\ 0 & 0 & 0\end{bmatrix} A=∂Xr∂f(Xr,ur)= ∂xr∂f1∂xr∂f2∂xr∂f3∂yr∂f1∂yr∂f2∂yr∂f3∂φr∂f1∂φr∂f2∂φr∂f3 = 000000−vrsinφrvrcosφr0
B = ∂ f ( X r , u r ) ∂ u r = [ ∂ f 1 ∂ v r ∂ f 1 ∂ δ r ∂ f 2 ∂ v r ∂ f 2 ∂ δ r ∂ f 3 ∂ v r ∂ f 3 ∂ δ r ] = [ cos φ r 0 sin φ r 0 tan δ r l v r l cos 2 δ r ] B=\frac{\partial f\left(X_r,u_r\right)}{\partial u_r}=\begin{bmatrix}\frac{\partial f_1}{\partial v_{r}} & \frac{\partial f_1}{\partial\delta_{r}}\\ \frac{\partial f_2}{\partial v_{r}} & \frac{\partial f_2}{\partial\delta_{r}}\\ \frac{\partial f_3}{\partial v_{r}} & \frac{\partial f_3}{\partial\delta_{r}}\end{bmatrix}=\begin{bmatrix}\cos\varphi_r & 0\\ \sin\varphi_r & 0\\ \frac{\tan\delta_r}{l} & \frac{v_r}{l\cos^2\delta_r}\end{bmatrix} B=∂ur∂f(Xr,ur)= ∂vr∂f1∂vr∂f2∂vr∂f3∂δr∂f1∂δr∂f2∂δr∂f3 = cosφrsinφrltanδr00lcos2δrvr
三、离散化
为了方便使用递推式进行迭代,我们还需要对线性化后的结果进行离散化,用差商代替微分,如下所示:
X ~ ˙ = X ~ ( k + 1 ) − X ~ ( k ) T = A X ~ ( k ) + B u ~ ( k ) \dot{\widetilde{X}}=\frac{\widetilde{X}(k+1)-\widetilde{X}(k)}{T}=A\widetilde{X}(k)+B\widetilde{u}(k) X ˙=TX (k+1)−X (k)=AX (k)+Bu (k)
所以:
X ~ ( k + 1 ) = ( I + T A ) X ~ ( k ) + T B u ~ ( k ) \widetilde{X}(k+1)=(I+TA)\widetilde{X}(k)+TB\widetilde{u}(k) X (k+1)=(I+TA)X (k)+TBu (k)
我们定义 A ~ = ( I + T A ) \widetilde{A}=(I+TA) A =(I+TA), B ~ = T B \widetilde{B}=TB B =TB,则上式可写为:
X ~ ( k + 1 ) = A ~ X ~ ( k ) + B ~ u ~ ( k ) \widetilde{X}(k+1)=\widetilde{A}\widetilde{X}(k)+\widetilde{B}\widetilde{u}(k) X (k+1)=A X (k)+B u (k)
由前面推出的A和B的结果,容易得知:
A ~ = [ 1 0 − T v r sin φ r 0 1 T v r cos φ r 0 0 1 ] \widetilde{A}=\begin{bmatrix}1& 0 & -Tv_r\sin\varphi_{r}\\ 0 & 1 & Tv_r\cos\varphi_{r}\\ 0 & 0 & 1\end{bmatrix} A = 100010−TvrsinφrTvrcosφr1
B ~ = [ T cos φ r 0 T sin φ r 0 T tan δ r l T v r l cos 2 δ r ] \widetilde{B}=\begin{bmatrix}T\cos\varphi_r & 0\\ T\sin\varphi_r & 0\\ \frac{T\tan\delta_r}{l} & \frac{Tv_r}{l\cos^2\delta_r}\end{bmatrix} B = TcosφrTsinφrlTtanδr00lcos2δrTvr
至此,我们已经得到完整的离散化的状态空间表达式,上面式子中带有较多的差值符号 ~,这是因为在第二部分中将状态量和输入量分别取为 X = [ x y φ ] T X=[x\ y\ φ]^T X=[x y φ]T,控制输入为 u = [ v δ ] T u=[v \ δ]^T u=[v δ]T导致的, 所以,现在我们直接将状态量和输入量取为当前量与期望值的差值,即
X = [ x c − x r y c − y r φ c − φ r ] , u = [ v c − v r δ c − δ r ] {{X}}=\begin{bmatrix}{x_{c}}-x_{r}\\ {y_c}-{y}_{r}\\ {\varphi_c}-{\varphi}_{r}\end{bmatrix},\mathbf{{u}}=\begin{bmatrix}v_{c}-v_{r}\\ \delta_{c}-\delta_{r}\end{bmatrix} X= xc−xryc−yrφc−φr ,u=[vc−vrδc−δr]
此时:
X ( k + 1 ) = [ 1 0 − T v r sin ψ r 0 1 T v r cos ψ r 0 0 1 ] X ( k ) + [ T cos ψ r 0 T sin ψ r 0 T tan δ r l T v r l cos 2 δ r ] u ( k ) = A X ( k ) + B u ( k ) \begin{aligned}\mathbf{X}(\mathrm{k}+1) & \left.=\left[\begin{array}{ccc}1 & 0 & -\mathrm{Tv}_{\mathrm{r}}\sin\psi_{\mathrm{r}}\\ 0 & 1 & \mathrm{Tv}_{\mathrm{r}}\cos\psi_{\mathrm{r}}\\ 0 & 0 & 1\end{array}\right.\right]\mathbf{X}(\mathrm{k})+\left[\begin{array}{ccc}\mathrm{T}\cos\psi_{\mathrm{r}} & 0\\ \mathrm{T}\sin\psi_{\mathrm{r}} & 0\\ \frac{\mathrm{T}\tan\delta_{\mathrm{r}}}{l} & \frac{T\mathrm{v}_{\mathrm{r}}}{l\cos^2\delta_{\mathrm{r}}}\end{array}\right]\mathbf{u}(\mathrm{k})\\ & \mathrm{=AX(k)+Bu(k)}\end{aligned} X(k+1)= 100010−TvrsinψrTvrcosψr1 X(k)+ TcosψrTsinψrlTtanδr00lcos2δrTvr u(k)=AX(k)+Bu(k)
有了上面的离散化线性运动学模型的状态空间方程,就可以基于此来使用LQR、MPC等控制算法进行轨迹跟踪控制或完成其他控制任务了
参考资料:
1、【控制】模型预测控制 MPC 【合集】Model Predictive Control




