509. 斐波那契数

class Solution {
    public int fib(int n) {
   		//用公式推至少得两个数
        if(n==0 || n==1) return n;

        int[] dp = new int[n+1];
        dp[0]=0;
        dp[1]=1;
        for(int i=2; i<=n; i++){
            dp[i]=dp[i-1]+dp[i-2];
        }

        return dp[n];
    }
}

70. 爬楼梯

n = 1 时，有 1 种走法：1
n = 2 时，有 2 种走法：1+1，2
n = 3 时，有 3 种走法：1+1+1，1+2，2+1

因为每次只能走 1 步或者 2 步，所以 n=3 时的最后一步有两种走法：

• 从第 1 个台阶走 2 步到达；
• 从第 2 个台阶走 1 步到达

所以 n = 3 时的方案是 n = 1和 n = 2 的方案之和。后面 n=其他值时，道理也一样。所以本体可以用动态规划。

class Solution {
    public int climbStairs(int n) {

        if(n==1 || n==2) return n;

        int[] dp = new int[n+1];
        dp[1]=1;
        dp[2]=2;
        for(int i=3; i<=n; i++){
            dp[i]=dp[i-1]+dp[i-2];
        }

        return dp[n];
    }
}

746. 使用最小花费爬楼梯

因为支付一次费用可以爬 1 或 2 个台阶，所以到达顶楼（记为台阶 n）有两种方案：从台阶 n-2 支付后走两个台阶到台阶 n；从台阶 n-1 支付后走一个台阶到台阶 n

如果现在有从头走到台阶 n-2 和台阶 n-1 需要的最小花费为 dp[n-2] 和 dp[n-1]，那么走到台阶 n 的最小花费为：dp[n]=min(dp[n-2]+cost[n-2], dp[n-1]+cost[n-1])

如果初始化 dp[1]、dp[2]，就可以按照上面的式子递推出走到顶楼（台阶 n）需要的最小花费

class Solution {
    public int minCostClimbingStairs(int[] cost) {

        int n=cost.length;
        if(n==1) return 0;//可以省略
        if(n==2) return Math.min(cost[0], cost[1]);//可以省略

        int[] dp = new int[n+1];
        dp[1]=0;
        dp[2]=Math.min(cost[0], cost[1]);
        for(int i=3; i<=n; i++){
            dp[i]=Math.min(dp[i-2]+cost[i-2], dp[i-1]+cost[i-1]);
        } 
        return dp[n];
    }
}

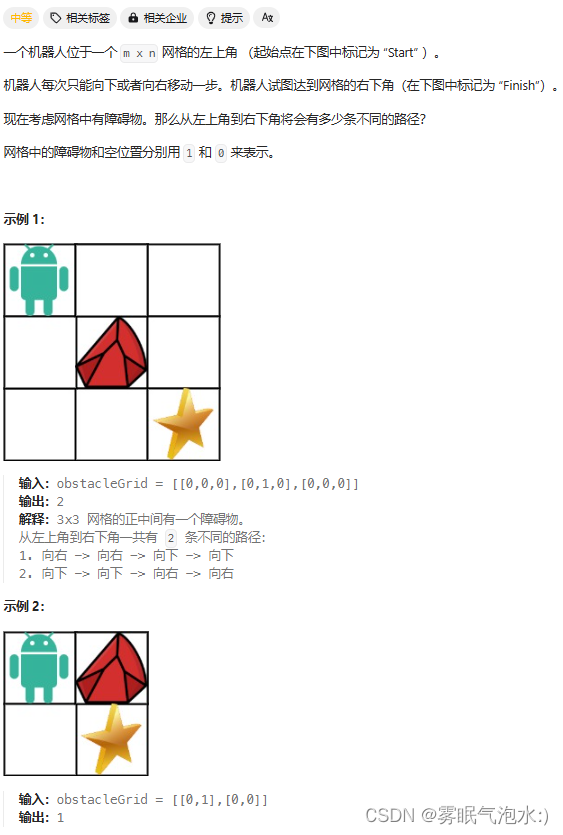
62. 不同路径

从右下角 finish 的上一个位置到达右下角有两种方式：

• 从上边位置向下走
• 从左边位置向右走

dp[i][j]：从左上角(0,0)到(i,j)有多少条不同路径
因此，可以得出递推公式：dp[i][j]=dp[i-1][j]+dp[i][j-1]。

但是，因为机器人只能向下或向右走，第 0 行的所有位置只能从左边的位置向右走到达，第 0 列的所有位置也只能从上边的位置向下走到达。所以这两种情况不能用上面的递推公式，可以直接初始化 dp 为 1，因为它们都只有一种到达方式。

剩余的其他位置就可以使用上面的递推公式来计算有几种到达方式。

class Solution {
    public int uniquePaths(int m, int n) {
        // dp[i][j]：从左上角(0,0)到(i,j)有多少条不同路径
        int[][] dp = new int[m][n];
        for(int i=0; i<m; i++) dp[i][0]=1;
        for(int j=0; j<n; j++) dp[0][j]=1;
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
}

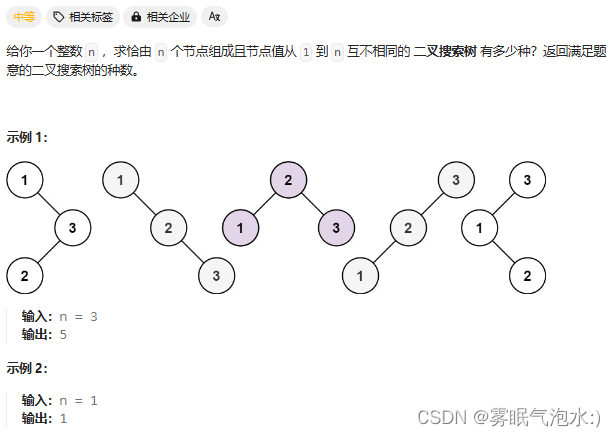
63. 不同路径 II

本题与上题的不同就是某些位置有障碍。如果起点或终点有障碍，机器人就无法到达终点，直接返回 0。否则开始递推。

dp[i][j]：从左上角(0,0)到(i,j)有多少条不同路径

对于有障碍或不能到达的位置，记 dp[i][j]=0，这样，后面的位置即使加上这种到达方式，也不会对最后的结果产生增益。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m=obstacleGrid.length;
        int n=obstacleGrid[0].length;
        
        if(obstacleGrid[0][0]==1 || obstacleGrid[m-1][n-1]==1) 
            return 0;
        
        // dp[i][j]：从左上角(0,0)到(i,j)有多少条不同路径
        int[][] dp = new int[m][n];
        //第0行和第0列中，有障碍的位置以及障碍之后的位置都不赋值，保持原来的0
        for(int i=0; i<m && obstacleGrid[i][0]==0; i++) dp[i][0]=1;
        for(int j=0; j<n && obstacleGrid[0][j]==0; j++) dp[0][j]=1;
        for(int i=1; i<m; i++){
            for(int j=1; j<n; j++){
            	//只有无障碍的位置才计算，否则保持原来的0
                if(obstacleGrid[i][j]==0){
                    dp[i][j]=dp[i-1][j]+dp[i][j-1];
                }               
            }
        }
        return dp[m-1][n-1];
    }
}

343. 整数拆分

dp[i]：正整数 i 拆分后的结果的最大乘积

class Solution {
    public int integerBreak(int n) {
        //dp[i]: 正整数i拆分后的结果的最大乘积
        int[] dp = new int[n+1];
        //dp[0]和dp[1]没有意义, 所以从dp[2]开始
        dp[2]=1;
        for(int i=3; i<=n; i++){
            // 把i按照多种方案进行拆分，举个例子：
            // j=2: j*(i-j)、j*(i-j)拆分, 这里dp[i-j]表示i-j拆分后乘积的最大值
            // j=2时各种拆分方案要与之前j=1时的最佳拆分方案对比，再选一个最佳的，赋给dp[i]
            // 这里有个优化，原理是i至少要拆分为两个数，两个数相近时两数乘积最大
            // 拆分为多个数时也是数值相近乘积最大，所以最多遍历到i/2就i可以了
            for(int j=1; j<=i/2; j++){
                dp[i]=Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
            }
        }
        return dp[n];
    }
}

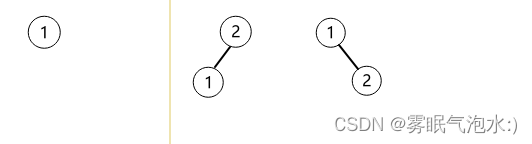
96. 不同的二叉搜索树

n = 1 与 n = 2 时，不相同的二叉搜索树的情况：

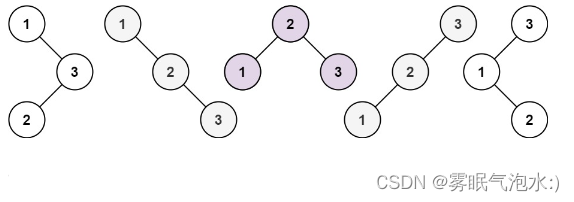
n = 3 时：

因为二叉搜索树有递归的性质，也就是一棵二叉搜索树的左子树和右子树都是一棵二叉搜索树。所以可以抓住这个特点来分析。

可以看到，n=3 时，二叉搜索树可以分别使用 1、2、3 作为根节点。

• 使用 1 作为根节点时，不同二叉搜索树的数量：n=0 时二叉搜索树的数量 * n=2 时二叉搜索树的数量

• 使用 2 作为根节点时，不同二叉搜索树的数量：n=1 时二叉搜索树的数量 * n=1 时二叉搜索树的数量

• 使用 3 作为根节点时，不同二叉搜索树的数量：n=2 时二叉搜索树的数量 * n=0 时二叉搜索树的数量

所以，当 n=0，n=1，n=2 二叉搜索树的数量都已知时，可以推断出 n=3 时二叉搜索树的数量，就是三种情况的和。

设 dp[n] 为：当有 n 个节点时，不同二叉搜索树有多少种。

class Solution {
    public int numTrees(int n) {
        if(n==0 || n==1) return 1;
        if(n==2) return 2; 

        int[] dp = new int[n+1];
        dp[0]=1;
        dp[1]=1;
        dp[2]=2;
        for(int i=3; i<=n; i++){
            dp[i]=0;//不初始化也是0
            for(int j=0; j<=i-1; j++){
                dp[i]+=dp[j]*dp[i-1-j];
            }
        }
        return dp[n];
    }
}

01背包理论基础

01 背包：有 n 种物品，每种物品只有一个
完全背包：有 n 种物品，每种物品有无限个
完全背包问题可以转换为 01 背包来解决

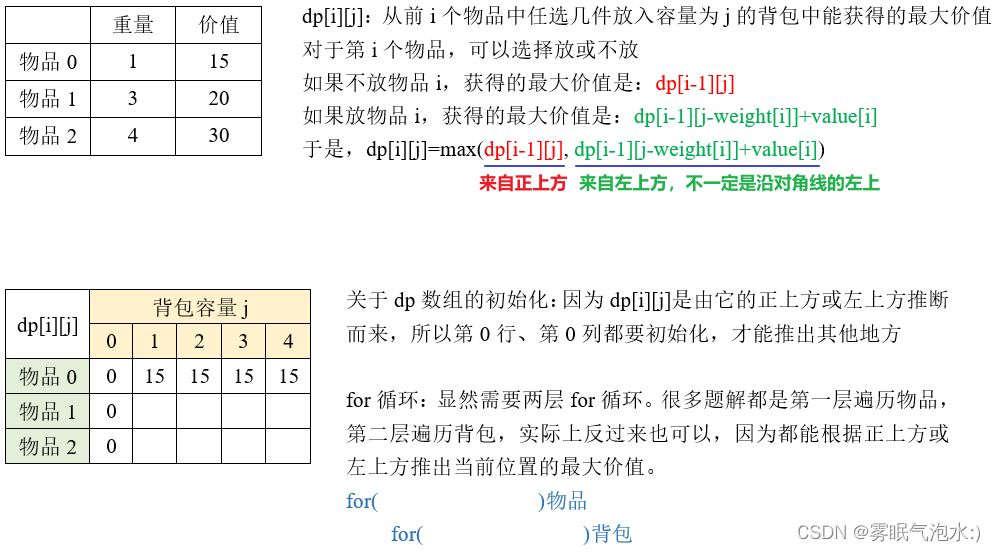
01 背包的二维数组解法

01 背包的滚动数组解法

• 要根据上一行计算下一行，实际是直接在原数组上修改。所以第一层 for 循环遍历物品
• 第二层 for 循环是在计算背包容量为各个值时，能装的最大价值。如果背包容量小于当前物品重量，则装不下该物品，且更小的背包也装不下，所以该层终止循环。
• 为什么第二层 for 循环倒序遍历？因为是在原数组上继续计算，且当前位置的结果来源于当前位置（原正上方）或前面的位置（原左上方），如果正序遍历就会导致前面位置上的数据被更新，当前位置就不能根据原左上方的数据计算了。
• 关于初始化：将 dp 数组元素全部初始化为 0。dp[0] 初始化为 0 好理解，其他元素初始化为 0 可以结合递推公式理解，是因为后续要通过取最大值来更新

416. 分割等和子集

数组元素和的一半可以看成一个背包，针对每一个数据，无非就是装与不装。如果能装满这个背包，说明数组能分成两个和相等的子集。

class Solution {
    public boolean canPartition(int[] nums) {
        int ans = sum(nums);
        // 数组和是奇数，一定不能分成两个和相等的子集
        if(ans%2!=0){
            return false;
        }

        int bagSize=ans/2;
        int[] dp = new int[bagSize+1];
        for(int i=0; i<nums.length; i++){
            for(int j=bagSize; j>=nums[i]; j--){
            	//取最大值就是尽力去装，最后再进行判断
            	//如果==target就代表装满了，证明有解
                dp[j]=Math.max(dp[j], dp[j-nums[i]]+nums[i]);
                // 剪枝也可
                // if(dp[bagSize]==bagSize) return true;
            }
        }
        return dp[bagSize]==bagSize;
    }

    private int sum(int[] arr){
        int ans=0;
        for(int i=0; i<arr.length; i++){
            ans+=arr[i];
        }
        return ans;
    }
}