【 1. 层次分析法简介 】

• 层次分析法（AHP） ：
  美国运筹学家匹茨堡大学教授萨蒂于上世纪70年代初，为美国国防部研究 “根据各个工业部门对国家福利贡献大小而进行电力分配” 课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。
  （ 决策是指在面临多种方案时需要依据一定的标准选择某一种方案 ）
• 特点：
  在对复杂的决策问题的本质、影响因素及其内在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多维度或无结构特性的复杂决策问题提供简便的决策方法。是对难以完全定量的复杂系统做出决策的模型和方法。
• 问题举例：

1. 在海尔、新飞、容声和雪花四个品牌的电冰箱中选购一种，要考虑品牌的信誉、冰箱的功能、价格和耗电量。
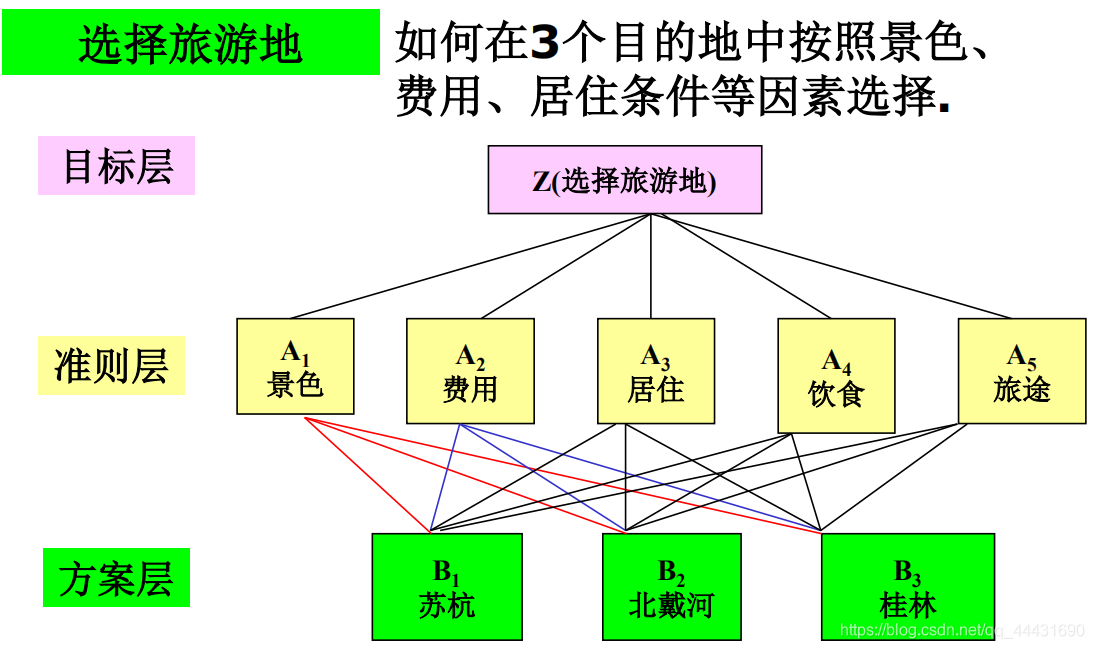
2. 在苏杭、北戴河、桂林三处选择一个旅游点，要考虑景点的景色、居住的环境、饮食的特色、交通便利和旅游的费用。

【 2. 层次分析法原理 】

1. 层次分析法根据问题的性质和要达到的总目标，将问题分解为不同的组成因素。
2. 按照因素间的相互关联影响以及隶属关系 将因素按不同层次聚集组合，形成一个多层次的分析结构模型。
3. 从而最终使问题归结为最低层(供决策的方案、措施等)相对于最高层(总目标)的相对重要权值的确定或相对优劣次序的排定。

【 3. 层次分析法步骤 】

运用层次分析法构造系统模型时，大体可以分为以下四个步骤：

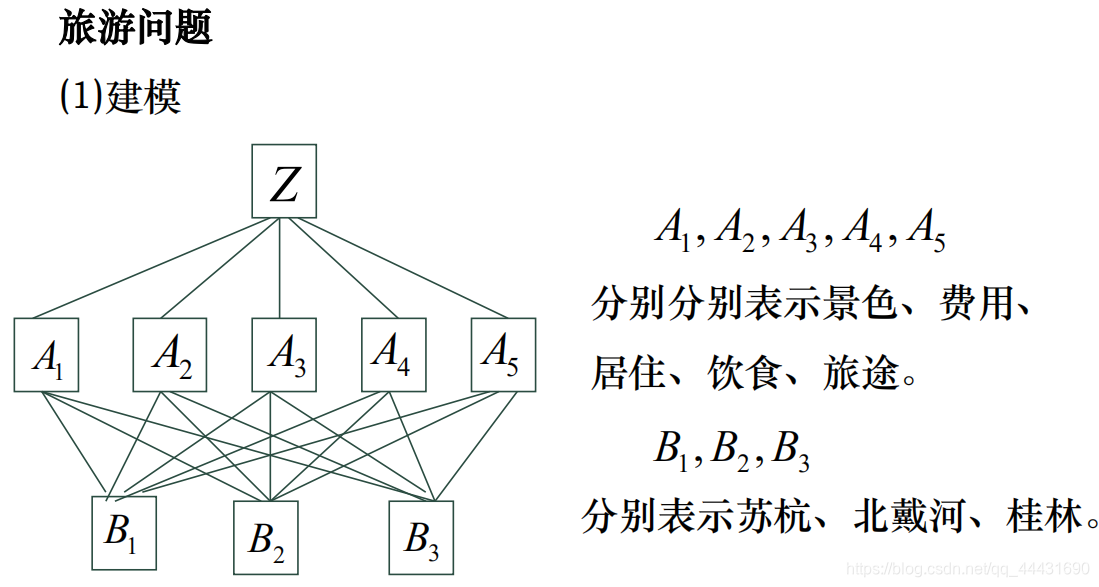
1. 建立层次结构模型
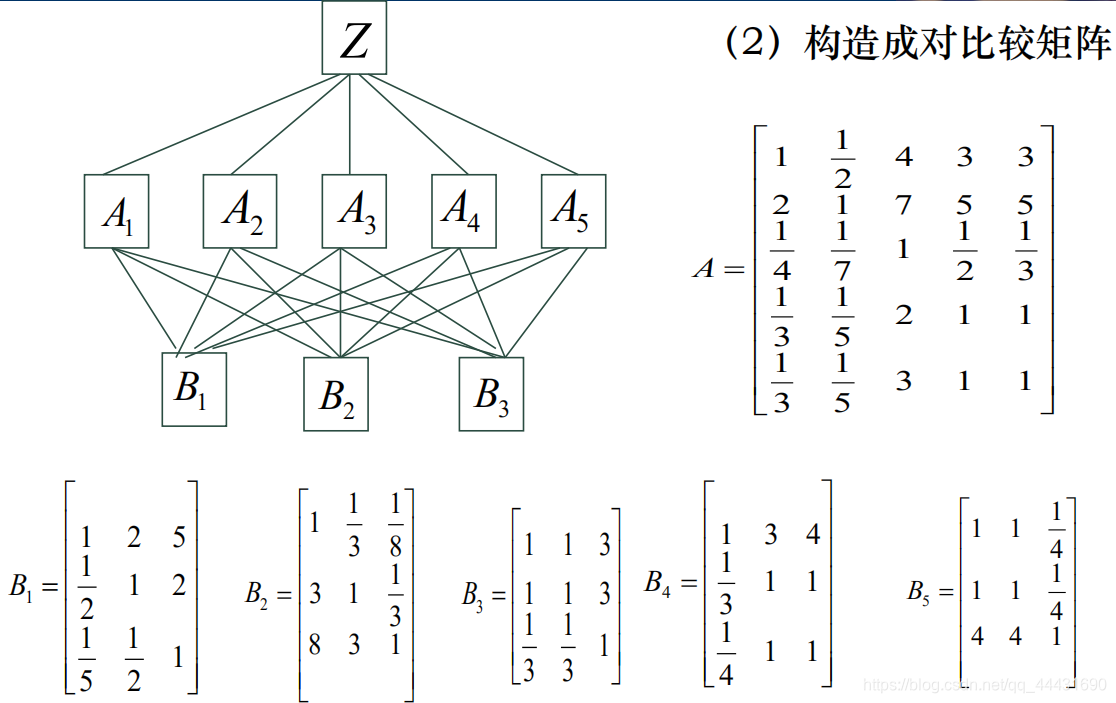
2. 构造判断(成对比较)矩阵
3. 层次单排序及其一致性检验
4. 层次总排序及其一致性检验

1. 建立层次结构模型

将决策的目标、考虑的因素(决策准则)和决策对象按它们之间的相互关系分为最高层、中间层和最低层，绘出层次结构图。
最高层:：决策的目的、要解决的问题。
最低层：决策时的备选方案。
中间层：考虑的因素、决策的准则。

• 例如：
  

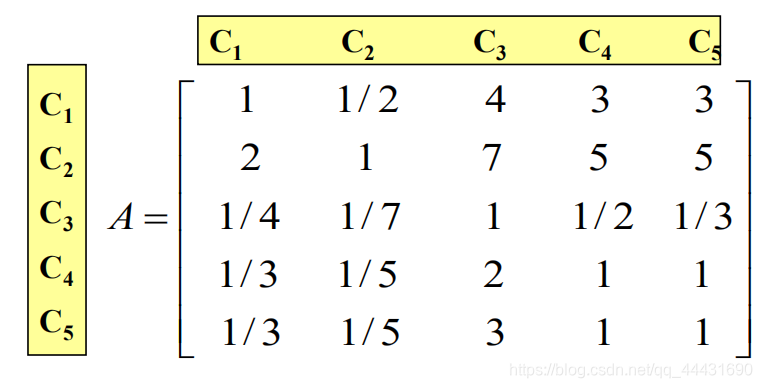
2. 成对比较矩阵

在确定各层次各因素之间的权重时，如果只是定性的结果,则常常不容易被别人接受，因而Santy等人提出一致矩阵法 ,即:

1. 不把所有因素放在一起比较，而是两两相互比较。

2. 对此时采用相对尺度，以尽可能减少性质不同的诸因素相互比较的困难，以提高准确度。

3. 成对比较矩阵是表示本层所有因素针对上一层某一个因素的相对重要性的比较。

4. 成对比较矩阵矩阵的元素 a_ij 用Santy的1~9标度方法给出。

5. 成对比较阵标度表
   

• 例如：
  

3. 一致性检验

【 4. 模型求解范例 】

$A[i][j]表示i相对于j对于Z的重要性。$
$B_n[i][j]表示i相对于j对于A_n的重要性。$

【 5. Matlab描述 】

disp('请输入判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
x=ones(n,100);
y=ones(n,100);
m=zeros(1,100);
m(1)=max(x(:,1));
y(:,1)=x(:,1);
x(:,2)=A*y(:,1);
m(2)=max(x(:,2));
y(:,2)=x(:,2)/m(2);
p=0.0001;i=2;k=abs(m(2)-m(1));
while  k>p
  i=i+1;
  x(:,i)=A*y(:,i-1);
  m(i)=max(x(:,i));
  y(:,i)=x(:,i)/m(i);
  k=abs(m(i)-m(i-1));
end
a=sum(y(:,i));
w=y(:,i)/a;
t=m(i);
disp(w); % w表示了底层对上层的权重
         %以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];
CR=CI/RI(n);
if CR<0.10
    disp('此矩阵的一致性可以接受!');
    disp('CI=');disp(CI);
    disp('CR=');disp(CR);
end