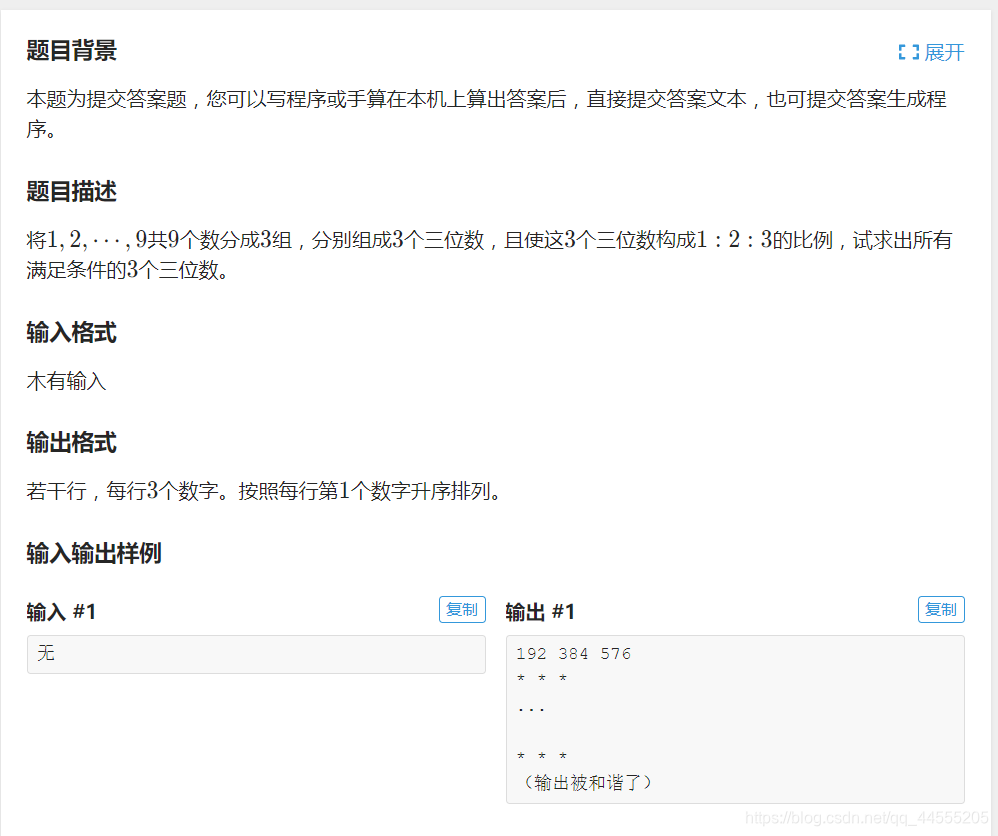
这道题我记得好像啊哈算法上面讲过dfs；哎呀反正不管了；重新写一遍也是好的；
我利用的向量来存的数字；以个数为结束条件来的dfs；为什么呢？
dfs思路：比如：
1 2 3 这三个数，他的全排列有哪些？ 1 2 3 ，1 3 2 ， 2 1 3 ，2 3 1， 3 1 2, 3 2 1；就这几种，其实就是利用dfs的思想排出来的；
因为当你标记1已经放到第一个位置时，那么第二个你就标记2放入第二个位置，然后第三个你就标记3放入第三个位置，之后返回到取消3的标记返回到上一层，那么就是把3放到2位置上，然后2放到3位置上；基本dfs思路就是这样滴；
所以AC代码：

#include<bits/stdc++.h>
using namespace std;
vector<int> Ve;
int book[10];
int gcd(int a,int b){
	return b?gcd(b,a%b):a;
}
void dfs(int num){
	  if(num==9){//如果9个数填满了
	  	int A=0,B=0,C=0;
	     for(int i=0;i<9;i++){//这里计算一下值就行了
	     	  if(i<3){
	     	  	  A=A*10+Ve[i];
			   }else if(i<6){
			   	  B=B*10+Ve[i];
			   }else if(i<9){
			   	  C=C*10+Ve[i];
			   }
			   int t1=gcd(A,B),t2=gcd(B,C);//其实这里可以不用算gcd的；
			   if(2*A/t1==B/t1&&3*B/t2==2*C/t2){//成比例，用笔算一下或者想一下就可以知道这个等式
			   	  printf("%d %d %d\n",A,B,C);
			   } 
		 }
	     return ;	
	  }
	  for(int i=1;i<=9;i++){
	  	   if(!book[i]){
	  	   	book[i]=1;
	  	   	  Ve.push_back(i);
	  	   	  dfs(num+1);
	  	   	  book[i]=0;
	  	   	  Ve.pop_back();
			 }
	  }
}
int main(){
   dfs(0);
	return 0;
}