将将红黑树内的某一个节点删除，需要执行的操作依次是：

首先，将红黑树当作一颗二叉查找树，将该节点从二叉查找树中删除；

然后，通过"旋转和重新着色"等一系列来修正该树，使之重新成为一棵红黑树。

红黑树删除： 最多旋转三次

若删除为红色节点，直接删除（因为红黑树的性质是不能出现两个连续的红色节点，因此我们不需要判断待删节点的子节点以及父节点是否为红色节点，而且删除的红色节点不会打破每个子树上的黑色节点数量相同的性质）。

若待删节点为黑色节点，删除节点补上来的孩子为红色，直接把孩子图成黑色；

若补上来的孩子为黑色节点，进行调整，向兄弟借黑色节点：（分四种情况）

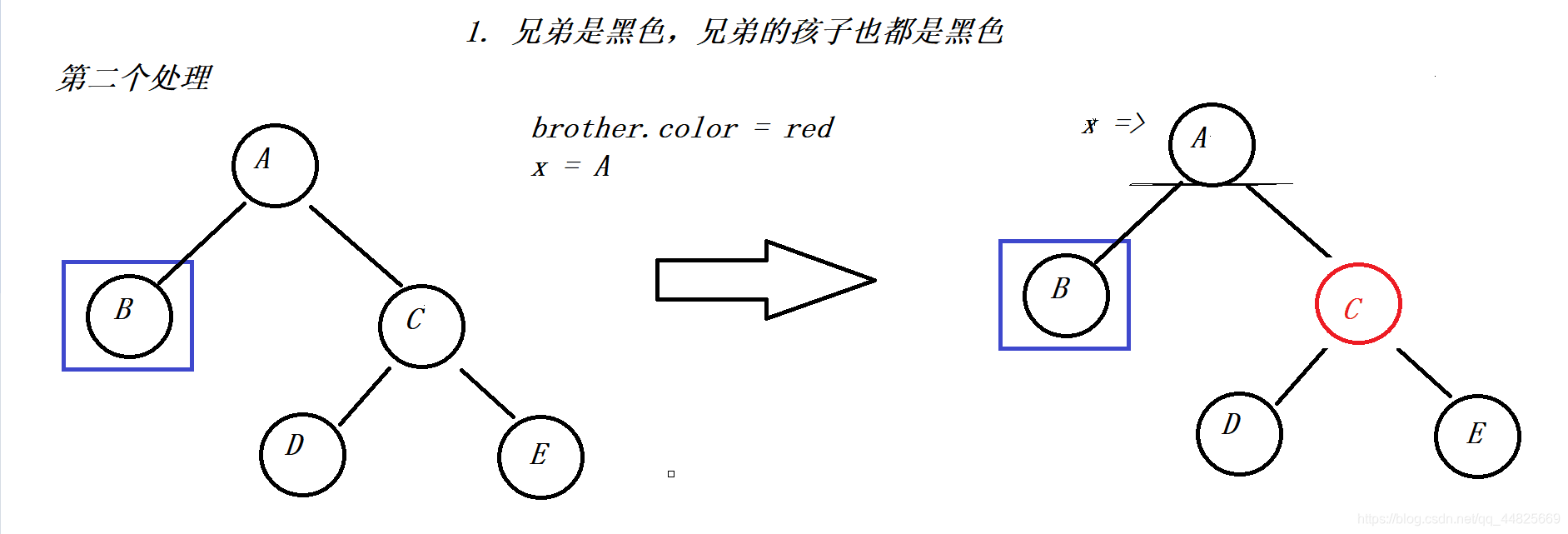
1.待删节点的兄弟是黑色，兄弟节点的子节点都是黑色的，无法向兄弟节点借颜色。操作是将兄弟节点置为红色，这样左右子树都缺一个黑色节点，相当于父节点缺一个黑色节点，指针指向父节点，重复操作

2.待删节点的兄弟节点是黑色的节点，且兄弟节点的左孩子是红色，右孩子是黑色（这里我们都已待删节点在左子树，兄弟节点在右子树为例），如果兄弟节点在左边的话，就是兄弟节点的右孩子是红色，左孩子是黑色。

   操作：将兄弟节点的颜色置为父节点颜色，将父节点置为黑色，将兄弟节点的右孩子置为黑色，再以父节点为根节点进行左旋操作

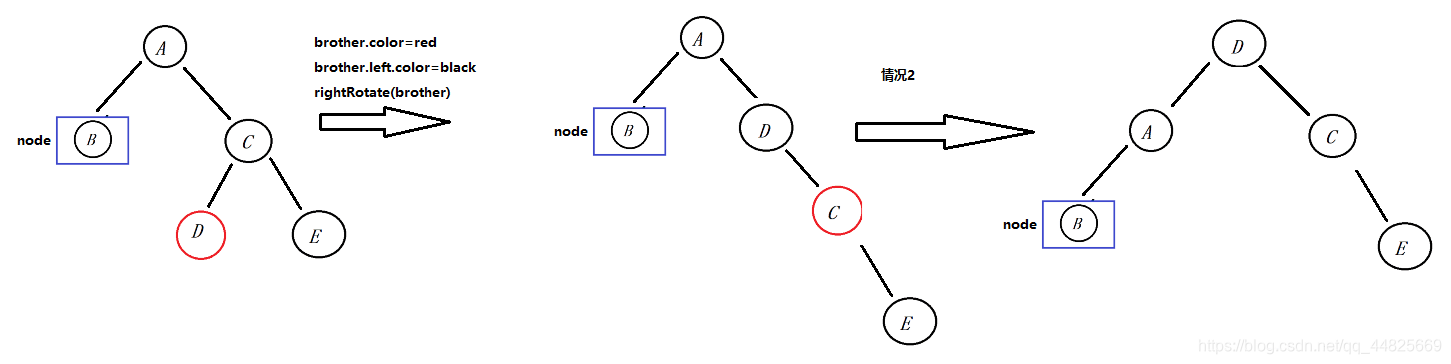
3.兄弟是黑色节点，兄弟节点的左孩子是红色，右孩子是黑色，（代码中体现就是兄弟节点的右孩子是）   

 操作：将兄弟节点置为红色，将兄弟节点的左孩子置为黑色，以兄弟节点为根节点进行左旋操作旋，旋转后变成了情况2，再以情况2的操作处理.

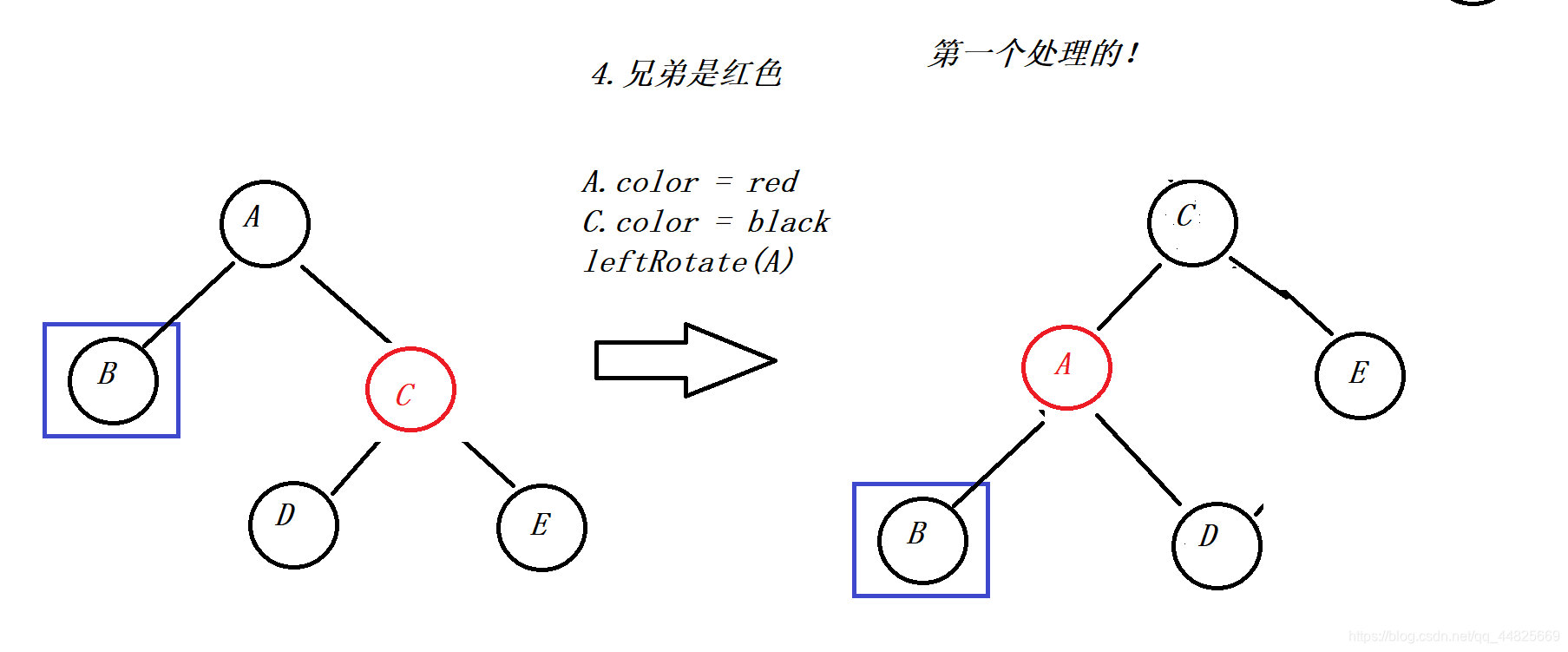
4.当兄弟节点为红色时，将父节点置为红色，兄弟节点置为黑色。然后以父节点为根节点进行左旋操作，下来就会变成兄弟节点为黑色的情况。

注意：上面的删除操作，都是以待删节点在左子树上，兄弟节点在右子树上为例，因此像情况2、3左红右黑与左黑右红当兄弟节点在左子树上时，情况刚好相反，旋转操作也是相反，因此我们只需要写出待删节点在左子树上的代码，然后修改一些变量就能得到待删节点在右子树上的情况

代码：

    public void remove(T data){
        if(this.root == null)
            return;

        RBNode<T> cur = this.root;
        while(cur != null){
            if(cur.getData().compareTo(data) > 0){
                cur = cur.getLeft();
            } else if(cur.getData().compareTo(data) < 0){
                cur = cur.getRight();
            } else {
                break;
            }
        }

        if(cur == null){
            return;
        }
        //删除有两个孩子的节点
        if(cur.getLeft() != null && cur.getRight() != null){
            RBNode<T> old = cur;
            cur = cur.getLeft();
            while(cur.getRight() != null){
                cur = cur.getRight();
            }
            old.setData(cur.getData());
        }

        // 删除cur指向的节点
        RBNode<T> child = cur.getLeft();
        if(child == null){
            child = cur.getRight();
        }
        if(child != null){
            child.setParent(cur.getParent());
            //删除节点为根节点
            if(cur.getParent() == null){
                this.root = child;
            } else {
                //将祖先节点和child连接起来
                //要删除节点为当前节点左孩子
                if(cur.getParent().getLeft() == cur){
                    cur.getParent().setLeft(child);
                } else {
                    cur.getParent().setRight(child);
                }
            }

            //有孩子补上来，用孩子作为删除结点调整。
            if(color(cur) == Color.BLACK){
                fixAfterRemove(child);
            }
        } else {
            //没有孩子的节点删除直接删除节点为根节点
            if(cur.getParent() == null){
                this.root = null;
            } else {
                //当没有孩子时，直接用删除结点进行调整，调整完再删除
                if(color(cur) == Color.BLACK){
                    fixAfterRemove(cur);
                }

                if(cur.getParent().getLeft() == cur){
                    cur.getParent().setLeft(null);
                } else {
                    cur.getParent().setRight(null);
                }
            }
        }
    }

    /**
     * 删除看兄弟节点情况
     * @param node
     */
    private void fixAfterRemove(RBNode<T> node) {
        while(color(node) == Color.BLACK){
            if(node == left(parent(node))){
                // 左子树删除黑色节点
                RBNode<T> brother = right(parent(node));
                if(color(brother) == Color.RED){ // 情况4
                    setColor(brother, Color.BLACK);
                    setColor(parent(node), Color.RED);
                    leftRotate(parent(node));
                    brother = right(parent(node));
                }

                if(color(left(brother)) == Color.BLACK // 情况1
                        && color(right(brother)) == Color.BLACK){
                    setColor(brother, Color.RED);
                    node = parent(node);
                } else {
                    // 情况3的前半段
                    if(color(right(brother)) != Color.RED){
                        setColor(brother, Color.RED);
                        setColor(left(brother), Color.BLACK);
                        rightRotate(brother);
                        brother = right(parent(node));
                    }

                    // 统一处理情况2
                    setColor(brother, color(parent(node)));
                    setColor(parent(node), Color.BLACK);
                    setColor(right(brother), Color.BLACK);
                    leftRotate(parent(node));
                    break;
                }
            } else {
                // 右子树删除黑色节点
                RBNode<T> brother = left(parent(node));
                if(color(brother) == Color.RED){ // 情况4
                    setColor(brother, Color.BLACK);
                    setColor(parent(node), Color.RED);
                    rightRotate(parent(node));
                    brother = left(parent(node));
                }

                if(color(left(brother)) == Color.BLACK // 情况1
                        && color(right(brother)) == Color.BLACK){
                    setColor(brother, Color.RED);
                    node = parent(node);
                } else {
                    // 情况3的前半段
                    if(color(left(brother)) != Color.RED){
                        setColor(brother, Color.RED);
                        setColor(right(brother), Color.BLACK);
                        leftRotate(brother);
                        brother = left(parent(node));
                    }

                    // 统一处理情况2
                    setColor(brother, color(parent(node)));
                    setColor(parent(node), Color.BLACK);
                    setColor(left(brother), Color.BLACK);
                    rightRotate(parent(node));
                    break;
                }
            }
        }
        // 在当前这一路遇见红色节点，直接补一个黑色节点
        setColor(node, Color.BLACK);
    }