A题 高压油管的压力控制

问题一:
稳定模型
如何设置单向阀每次开启的时长,使得高压油管内的压力尽可能稳定在 100 M P a 100MPa 100MPa左右。首先要明确高压油管的工作原理以及过程。燃油经过高压油泵从A处进入高压油管,再由喷口B喷出。燃油进入和喷出的间歇性工作过程会导致高压油管内压力的变化。
压力与密度关系
题目中给出燃油的压力变化量与密度变化量成正比,比例系数为 E ρ {\frac{E}{\rho} } ρE ,其中 ρ {\rho} ρ为为燃油的密度。
P k + 1 − P k = E ( P k ) ρ k ( ρ k + 1 − ρ k ) , k = 0 , 1 , 2 , ⋯ P_{k+1}-P_{k}=\frac{E\left(P_{k}\right)}{\rho_{k}}\left(\rho_{k+1}-\rho_{k}\right), k=0,1,2, \cdots Pk+1−Pk=ρkE(Pk)(ρk+1−ρk),k=0,1,2,⋯
首先要进行迭代计算,通过题目中所给压力与密度的出状态递推出燃油每一密度下的压力。这里实际用Excel表格就能操作:附件3-弹性模量与压力,在 C 1 C1 C1单元格填入 燃油密度 ( m m 3 / m s ) 燃油密度(mm3/ms) 燃油密度(mm3/ms), C 202 C202 C202填入 0.85 0.85 0.85,对应为 100 M P a 100MPa 100MPa压力下的密度。现在将 C 201 C201 C201填入公式: = ( B 201 ∗ C 202 ) / ( B 201 − A 201 + A 202 ) =(B201*C202)/(B201-A201+A202) =(B201∗C202)/(B201−A201+A202),上拉操作;将 C 203 C203 C203填入公式: = ( B 203 ∗ C 202 ) / ( B 203 − A 203 + A 202 ) ) =(B203*C202)/(B203-A203+A202)) =(B203∗C202)/(B203−A203+A202)),下拉操作,拉满位置,此时这一列数据为对应压力下的密度。
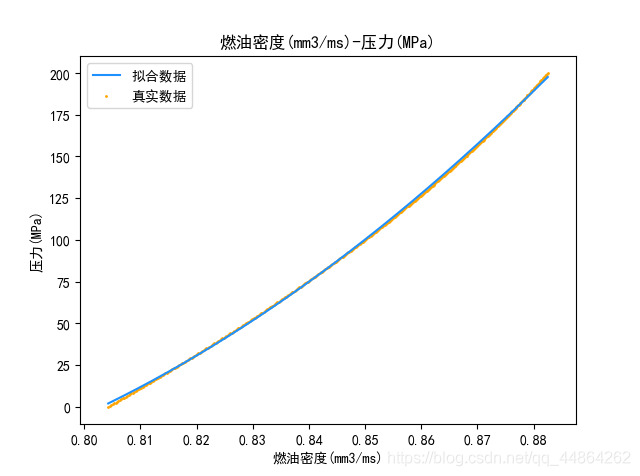
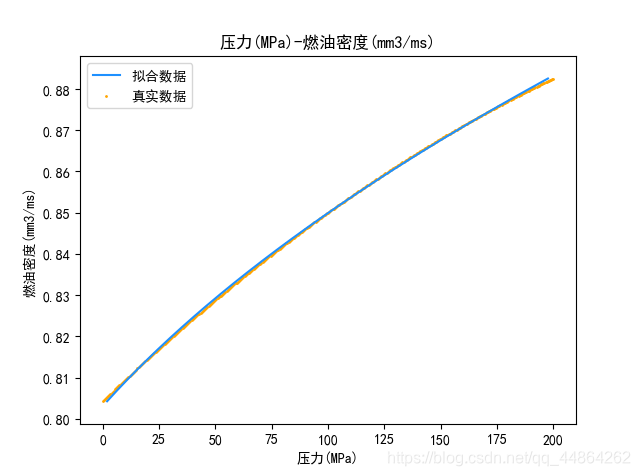
通过 p a n d a s pandas pandas库导入文件的两列数据,用 p o l y f i t polyfit polyfit函数进行数据拟合,这里比较简便,可以选择二次项或者三次项的系数,下面完整代码有体现到这一代码的实现。这里采用了二次函数拟合,效果还算理想,也可选择其他更良好的拟合方式,不过比较麻烦,这样后续的数据会更准确。
效果还可以哈。
P ( ρ ) = 10784.65349198 ρ 2 − 15693.86029255 ρ + 5648.09019803 P(\rho)=10784.65349198\rho^{2}-15693.86029255\rho+5648.09019803 P(ρ)=10784.65349198ρ2−15693.86029255ρ+5648.09019803
ρ ( P ) = 10784.65349198 P 2 − 15693.86029255 P + 5648.09019803 \rho(P)=10784.65349198P^{2}-15693.86029255P+5648.09019803 ρ(P)=10784.65349198P2−15693.86029255P+5648.09019803
高压油管内部压力变化
进气状态
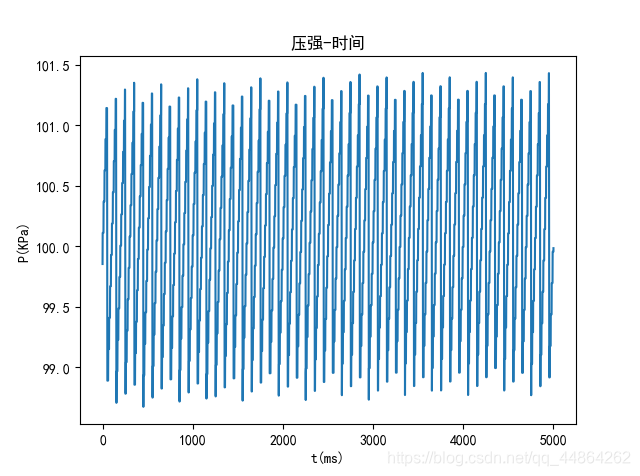
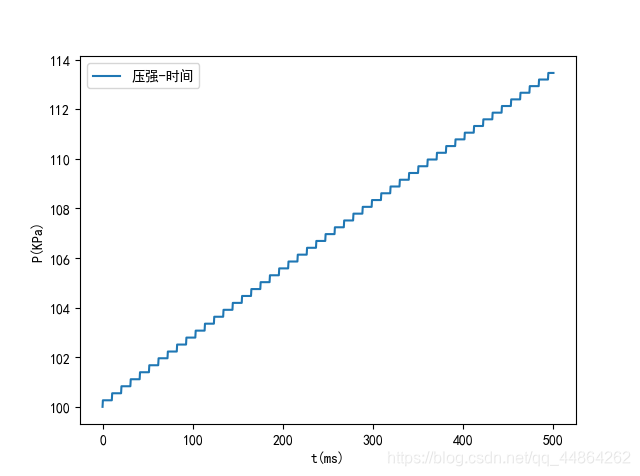
高压油管内的初始压力为 100 M P a 100MPa 100MPa,当高压油泵从A出进入高压油管时,高压油管内油气质量增大,体积不变,密度增大,此时高压油管内的压力增大。这是在起初一个较短时间内的状态。在开启了一段时长后(这段时长的参数是自己设置的,在后面要用到遍历及优化的思想,本题按 0.001 m s 0.001ms 0.001ms遍历搜索最佳时长为 0.288 m s 0.288ms 0.288ms) t1(0.288ms) 后,要关闭 10ms 。在进气阶段两个蓝色标注是非常重要的量,贯穿整个高压油管工作的始尾。下图取 500 m s 500ms 500ms为界,此时是高压油管只进行进气状态压强的变化图。
R j ( T p ) = { 0.85 × π × 0. 7 2 2 ( 160 − P j ) ρ ( 160 ) ρ ( 160 ) h 单向阀开启时 0 单向阀关闭时 R_{j}\left(T_{p}\right)=\left\{\begin{array}{ll} 0.85 \times \pi \times 0.7^{2} \sqrt{\frac{2\left(160-P_{j}\right)}{\rho(160)}} \rho(160) h& \text { 单向阀开启时 } \\ 0 & \text { 单向阀关闭时 } \end{array}\right. Rj(Tp)={ 0.85×π×0.72ρ(160)2(160−Pj)ρ(160)h0 单向阀开启时 单向阀关闭时
代码实现
# 进油函数 参数t为时刻,t1为进油时间段
def enter(t, t1):
global m, P, ρ # 全局变量,可做修改
if 0 < t % (t1 + 10) < t1:
Q = C * A * math.sqrt(2 * (160 - P) / ρ160) # 单位时间进油量
det_m = Q * ρ160 * t_ # 0.01为步长 质量改变量
m = m + det_m # 更新质量
rou = m / V_primary # 更新密度
P = ρ_P(rou) # 更新压强
else:
pass
进气过程展示
喷气状态
喷气状态题中已经给出状态图
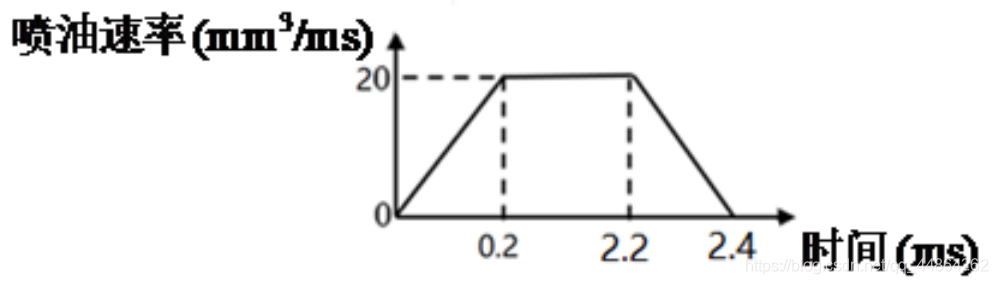
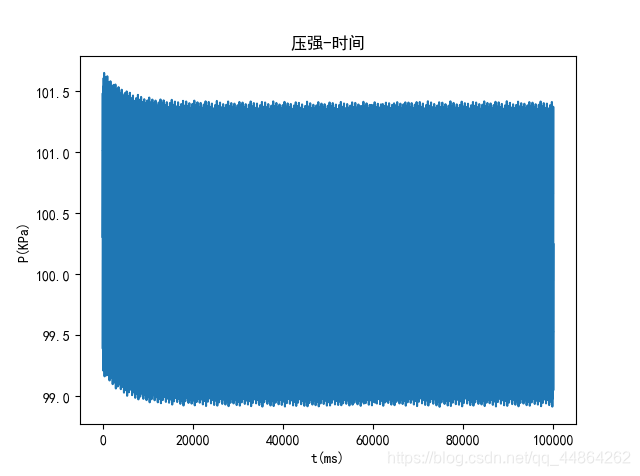
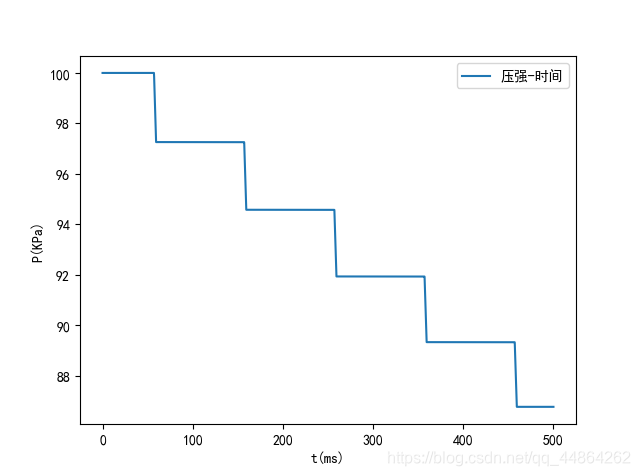
每 100 m s 100ms 100ms除了喷油嘴不工作的时间,其他时间都是在这个状态下进行的,喷油嘴喷气,高压油管内的燃油的体积不变,质量减小,密度减小,在这一时间段高压油管内的压力是减小的。这里比较重要的参数是时间段为 2.4 m s 2.4ms 2.4ms开始喷气的时间 t0(50ms) ,下图取 500 m s 500ms 500ms为界,此时是高压油管只进行喷气状态压强的变化图。
Q j ( T s ) = { 0 Mod ( t , 100 ) − T s < 0 100 ( Mod ( t , 100 ) − T s ) , 0 ≤ Mod ( t , 100 ) − T s < 0.2 ; 20 h 0.2 ≤ Mod ( t , 100 ) − T s < 2.2 ; ( 240 − 100 ( Mod ( t , 100 ) − T s ) ) h 2.2 ≤ Mod ( t , 100 ) − T s < 2.4 ; 0 2.4 ≤ Mod ( t , 100 ) − T s Q_{j}\left(T_{s}\right)=\left\{\begin{array}{ll} 0 & \operatorname{Mod}(t, 100)-T_{s}<0 \\ 100\left(\operatorname{Mod}(t, 100)-T_{s}\right) , & 0 \leq \operatorname{Mod}(t, 100)-T_{s}<0.2 ; \\ 20 h & 0.2 \leq \operatorname{Mod}(t, 100)-T_{s}<2.2 ; \\ \left(240-100\left(\operatorname{Mod}(t, 100)-T_{s}\right)\right) h & 2.2 \leq \operatorname{Mod}(t, 100)-T_{s}<2.4 ; \\ 0 & 2.4 \leq \operatorname{Mod}(t, 100)-T_{s} \end{array}\right. Qj(Ts)=⎩ ⎨ ⎧0100(Mod(t,100)−Ts),20h(240−100(Mod(t,100)−Ts))h0Mod(t,100)−Ts<00≤Mod(t,100)−Ts<0.2;0.2≤Mod(t,100)−Ts<2.2;2.2≤Mod(t,100)−Ts<2.4;2.4≤Mod(t,100)−Ts
这里使用了一个取余函数,非常精妙,确保每个周期的喷气状态与第一个喷气周期状态相等。
代码实现
# 出油函数 参数t为时刻,t0为出油时刻
def out(t, t0):
global m, P, ρ # 全局变量,可做修改
if t0 < (t % 100) < t0 + 0.2: # 第一段0~0.2ms
Q = (t - t0) % 100 * 100 # 在不同周期内时刻的流量
det_m = Q * ρ * t_ # 0.01为步长 质量改变量
m = m - det_m # 更新质量
ρ = m / V_primary # 更新密度
P = ρ_P(ρ) # 更新压强
elif t0 + 0.2 <= (t % 100) < t0 + 2.2: # 第二段0.2~2.2ms
Q = 20
det_m = Q * ρ * t_ # 0.01为步长 质量改变量
m = m - det_m # 更新质量
ρ = m / V_primary # 更新密度
P = ρ_P(ρ) # 更新压强
elif t0 + 2.2 <= (t % 100) <= t0 + 2.4: # 第三段2.2~2.4ms
Q = ((t - t0) * (-100) + 240) % 100
det_m = Q * ρ * t_ # 0.01为步长 质量改变量
m = m - det_m # 更新质量
ρ = m / V_primary # 更新密度
P = ρ_P(ρ) # 更新压强
else:
pass
进喷气状态结合
进气状态和喷气状态是一个相互的过程,在高压油管工作时,进喷气会存在同时进行的状态。这时只需更改喷气开始的时间 t0 与进气时长 t1 ,便可得到想要的结果,这里取 5000 m s 5000ms 5000ms的时长。
m i n ∑ k = 1 n ∣ P k − 100 ∣ = m i n ∑ k = 1 n ∣ ∑ j = 0 k − 1 E ( P j ) V ρ j ( R j ( T p ) − Q j ( T s ) ) min\sum_{k=1}^{n}|P_{k}-100|=min\sum_{k=1}^{n}|\sum_{j=0}^{k-1}\frac{E(P_{j})}{V\rho _{j}}(R_{j}(T_{p})-Q_{j}(T_{s})) min∑k=1n∣Pk−100∣=min∑k=1n∣∑j=0k−1VρjE(Pj)(Rj(Tp)−Qj(Ts))
关于进喷气函数的编程实现
整个过程是在 t = 0.01 m s t=0.01ms t=0.01ms的逐步递推进行的,首先要想到 t = 0 t=0 t=0的出状态,自己可以在纸上写一下,经过 t = 0.01 m s t=0.01ms t=0.01ms高压油管的状态是什么,经过 t = 0.01 m s + 0.01 m s = 0.02 m s t=0.01ms+0.01ms=0.02ms t=0.01ms+0.01ms=0.02ms高压油管的状态是什么,首先计算单位时间进油量,乘 160 M P a 160MPa 160MPa密度即为进入的质量,质量变化、体积不变、密度变化、压强变化,每走 0.01 m s 0.01ms 0.01ms更新一下高压油管内压强的状态,即可完成整个过程.
关于遍历及优化的编程实现
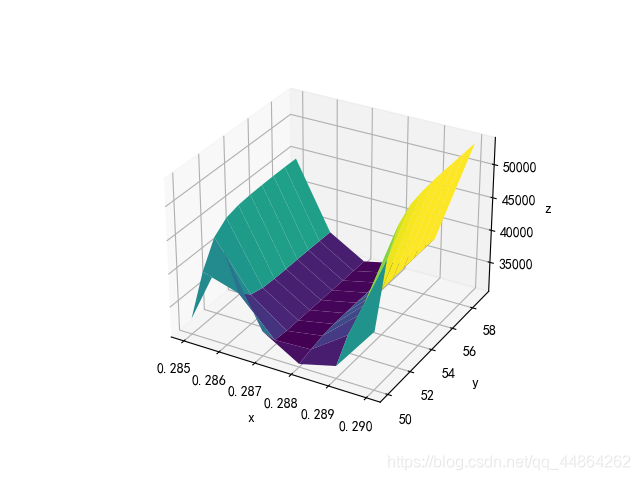
这个考虑到高压油管内部压强比较稳定,所以进喷气的质量大致相同,取质量相同求得 t 0 = 0.28 m s t0=0.28ms t0=0.28ms,在附近进行遍历即可。
优化这个可以自己设计,本题要求在 100 M P a 100MPa 100MPa较稳定的工作状态,我们可以计算整个函数与 P = 100 M P a P=100MPa P=100MPa的面积,面积越小时优化结果越好。但是在实际代码设计优化状态下可能会出现问题,这个我们还要自己把握。我的想法每遍历一次输出一张图片到文件夹里,然后打开文件夹翻阅查看,再通过那段区间设置优化的限制。
关于搜索结果图的做法
稳定模型完整代码
代码比较灵活,里面参数可以自行修改,在使用时要导入 p y t h o n python python第三方库。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import math
data = '附件3-弹性模量与压力.xlsx'
data = pd.read_excel('附件3-弹性模量与压力.xlsx') # 导入附件3数据
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
x_pandas_list = data[u'燃油密度(mm3/