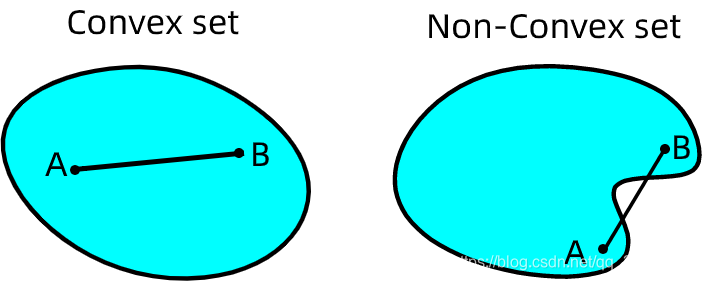
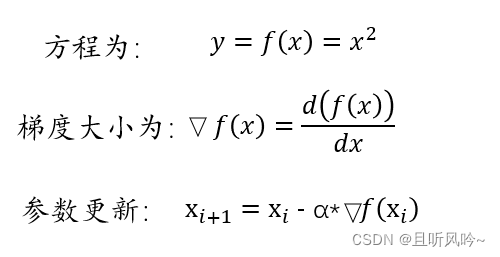凸（convex)：

• 指的是顺着梯度方向走到底就 一定是 最优解 。
• 大部分 传统机器学习 问题 都是凸的。

非凸(Non-convex)：

• 指的是顺着梯度方向走到底只能保证是局部最优，不能保证 是全局最优。
• 深度学习以及小部分传统机器学习问题都是非凸的。

1.集合的凸和非凸看任意连线有没有不在区域内，函数则有公式：

任何局部最优解即为全局最优解。通常使用一个局部优化算法，如贪婪算法（Greedy Algorithm）或梯度下降算法（Gradient Decent）来计算局部最优解。

实际问题中，判断是否凸优化问题可以参考以下几点：

目标函数f ff如果不是凸函数，则不是凸优化问题。
决策变量x xx中包含离散变量（0-1变量或整数变量），则不是凸优化问题。
约束条件写成g ( x ) ≤ 0 g(x)\le0g(x)≤0时，g gg如果不是凸函数，则不是凸优化问题。
常见的凸优化问题：

1. 线性规划(LP, Linear Programming)：

2. 二次规划(QP, Quadratic Programing)：

3. 二次约束的二次规划(QCCP, Quadratically Contrained Quaratic Programing)：

4. 半正定规划(SDP, Semidefinite Programing)：

非凸优化：

通常情况下较难求解，可行域集合可能存在无数个局部最优点，求解全局最优算法复杂度是指数级（NP hard）。

因为非凸优化的难度较高，可以考虑将非凸优化转化为凸优化问题解决：

• 修改目标函数，使之转化为凸函数。
• 抛弃一些约束条件，使新的可行域为凸集并且包含原可行域。

那什么又是梯度下降法呢，梯度就是最快、最大的“方向导数”，如以下公式：

 GA、SA、PSO三种算法的区别：

遗传算法

​ 全局搜索能力强，局部搜索能力较弱，往往只能得到次优解而不是最优解。

​ 研究发现，遗传算法可以用极快的速度达到最优解的90%以上，但是要达到真正的最优解需要花费很长时间，即局部搜索能力不足。

遗传算法步骤：

遗传算法的基本步骤包括：

• 初始化种群：根据问题的特性和要求，随机生成一定数量的解，作为初始的种群。
• 评估适应度：根据问题的评价函数，对每个解进行适应度评估，用于后续的选择和遗传操作。
• 选择操作：按照适应度大小，选择出一定数量的个体，作为下一代种群的父代。
• 遗传操作：通过交叉、变异等操作，生成下一代种群的子代。
• 重复步骤2~4，直到满足停止条件（如达到一定代数、找到最优解等）。

==差分进化算法==（相较于遗传算法）

鲁棒性更强、收敛速度更快，但是全局优化搜索能力不如遗传算法

==粒子群算法==

搜索速度快，参数设置容易，但是极其容易陷入局部最优解，因此一般需要使用期改进方法避免陷入局部最优解。

粒子群算法步骤：

==蚁群算法==

参数设置复杂，代码编写比较复杂，并且一般用于路径规划问题中；如果参数设置不当，很容易偏离优质解

==模拟退火算法==

全局寻优能力强(个人感觉其他能力并不出众，并且很慢)，适合搭配粒子群算法一起使用。

模拟退火算法的步骤如下：

• 降温：按照指定的退火速率 降低温度 ，并检查是否满足终止条件；
• 重复步骤3~6，直到满足终止条件。

在每个降温周期中，接受劣解的概率随着温度的下降而逐渐降低，从而逐渐收敛到全局最优解。不过模拟退火算法的效果和结果很大程度上取决于初始温度、退火速率和终止条件等参数的设置。