代码随想录算法训练营第18天| LeetCode654. 最大二叉树 | 617.合并二叉树 | 700.二叉搜索树中的搜索

“看清楚这个世界，并不能让这个世界变得更好。但可能让你在看清楚这个世界是个怎样的世界后，把自己变得更好。”

题目链接：654. 最大二叉树 - 力扣（LeetCode）

要根据给定的不重复整数数组 nums 构建最大二叉树，可以按照以下步骤进行递归构建：

找到数组中的最大值及其索引。
以最大值创建一个根节点。
递归地在最大值左边的子数组上构建左子树。
递归地在最大值右边的子数组上构建右子树。
返回构建的二叉树。

class Solution654 {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return build(nums, 0, nums.length - 1);
    }

    private TreeNode build(int[] nums, int left, int right){
        if (left > right) {
            return null; // 子数组为空时返回 null
        }

        // 找到当前子数组中的最大值及其索引
        int maxIndex = left;
        for (int i = left + 1; i <= right; i++) {
            if (nums[i] > nums[maxIndex]) {
                maxIndex = i;
            }
        }

        // 创建根节点
        TreeNode root = new TreeNode(nums[maxIndex]);

        // 递归构建左子树和右子树
        root.left = build(nums, left, maxIndex - 1);
        root.right = build(nums, maxIndex + 1, right);

        return root; // 返回构建的树
    }
}

题目链接：617. 合并二叉树 - 力扣（LeetCode）

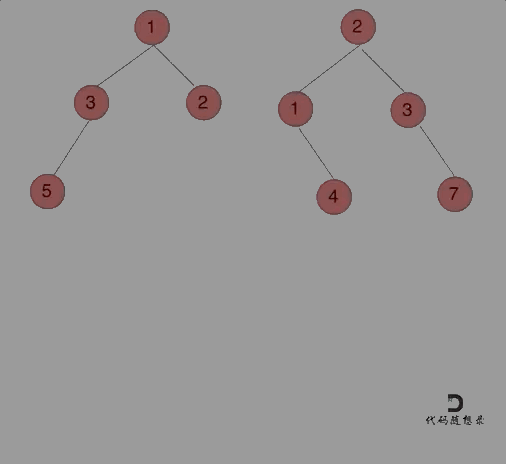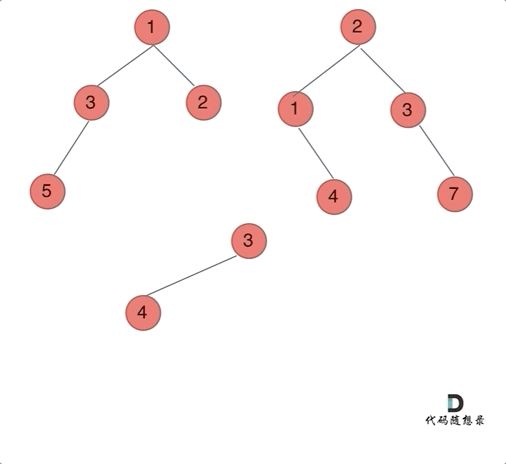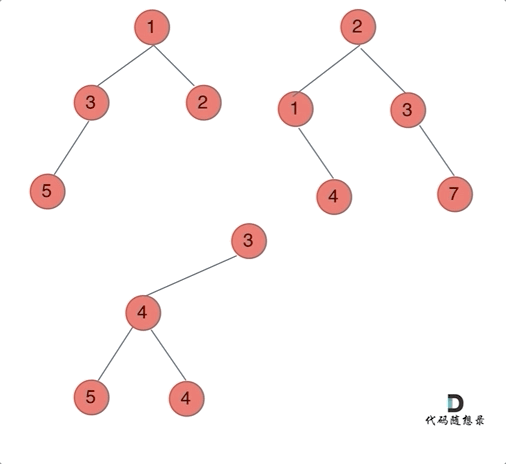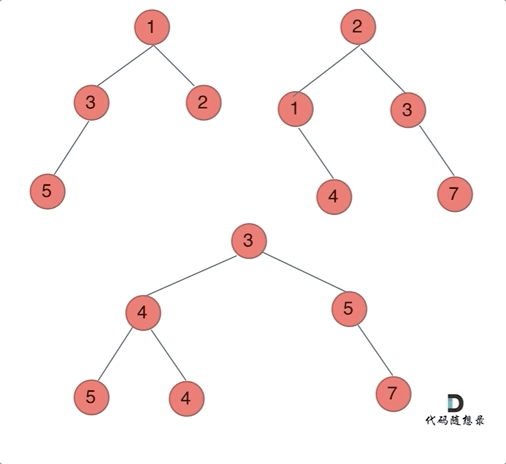
要将两棵二叉树合并成一棵新二叉树，可以使用递归的方法来实现。在递归过程中，我们处理如下几种情况：

如果 root1 和 root2 都为空，则返回空节点。
如果 root1 为空，直接返回 root2。
如果 root2 为空，直接返回 root1。
如果 root1 和 root2 都不为空，则创建一个新节点，其值为 root1 和 root2 节点值的和。然后递归地合并它们的左右子树。

以前序遍历为例：

class Solution617 {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if (root1 == null) {
            return root2; // 如果 root1 为空，返回 root2
        }
        if (root2 == null) {
            return root1; // 如果 root2 为空，返回 root1
        }

        // 如果两个节点都不为空，创建一个新节点，其值为两个节点值的和
        TreeNode newNode = new TreeNode(root1.val + root2.val);
        // 递归合并左子树
        newNode.left = mergeTrees(root1.left, root2.left);
        // 递归合并右子树
        newNode.right = mergeTrees(root1.right, root2.right);

        return newNode; // 返回合并后的新节点
    }
}

题目链接：700. 二叉搜索树中的搜索 - 力扣（LeetCode）

要在二叉搜索树（BST）中查找节点值等于给定值 val 的节点，可以利用BST的性质进行搜索：

对于每个节点，其左子树的所有节点值小于该节点值，其右子树的所有节点值大于该节点值。我们可以通过比较 val 和当前节点的值，决定是向左子树搜索还是向右子树搜索。

二叉搜索树是一个有序树：

若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉搜索树

这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。

本题，其实就是在二叉搜索树中搜索一个节点。

class Solution700 {
    public TreeNode searchBST(TreeNode root, int val) {
        // 如果根节点为空，或根节点的值等于目标值，返回根节点
        if (root == null || root.val == val) {
            return root;
        }

        // 如果目标值小于当前节点值，搜索左子树
        if (val < root.val) {
            return searchBST(root.left, val);
        }

        // 如果目标值大于当前节点值，搜索右子树
        return searchBST(root.right, val);
    }
}

题目链接：98. 验证二叉搜索树 - 力扣（LeetCode）

方法一：

要知道中序遍历下，输出的二叉搜索树节点的数值是有序序列。有了这个特性，验证二叉搜索树，就相当于变成了判断一个序列是不是严格单调递增的了。

class Solution98 {
    private TreeNode prev = null;
    public boolean isValidBST(TreeNode root) {
        return inOrderTraversal(root);
    }

    // 中序遍历二叉树并检查节点值是否严格递增
    private boolean inOrderTraversal(TreeNode node) {
        if (node == null) {
            return true;
        }

        // 递归遍历左子树
        if (!inOrderTraversal(node.left)) {
            return false;
        }

        // 检查当前节点值是否大于前一个节点值
        if (prev != null && node.val <= prev.val) {
            return false;
        }
        prev = node; // 更新前一个节点为当前节点

        // 递归遍历右子树
        return inOrderTraversal(node.right);
    }
}

方法二：

为了判断给定的二叉树是否是一个有效的二叉搜索树（BST），可以使用递归，通过比较每个节点的值，确保它符合BST的性质：左子树的所有节点值都小于当前节点值，右子树的所有节点值都大于当前节点值。此外，还需要确保所有子树也都是有效的BST。

可以通过递归遍历二叉树，并传递当前节点允许的最小值和最大值范围。

初始时，根节点的值范围是无穷小到无穷大。在递归过程中，我们不断更新这些范围，以确保每个节点的值符合BST的性质。

class Solution98 {
    public boolean isValidBST(TreeNode root) {
        return isValidBSTHelper(root, Long.MIN_VALUE, Long.MAX_VALUE);
    }

    // 递归方法，判断当前节点及其子树是否是有效的BST
    private boolean isValidBSTHelper(TreeNode node, long min, long max) {
        // 空节点是有效的BST
        if (node == null) {
            return true;
        }

        // 当前节点值必须在允许的范围内
        if (node.val <= min || node.val >= max) {
            return false;
        }

        // 递归检查左子树和右子树
        return isValidBSTHelper(node.left, min, node.val) &&
                isValidBSTHelper(node.right, node.val, max);
    }
}