文章目录
前言
本人初次学习时域离散信号与系统变换域分析
一、实验目的
1.了解时域离散信号的产生及基本运算实现。
2.掌握时域离散信号的傅里叶变换实现方法。
3.熟悉离散时间傅里叶变换性质。
4.掌握离散时间系统的Z域分析及稳定性判断方法。
5.提高运用软件分析、处理数字信号的能力。
6.使用Matlab软件平台,对时域离散信号与系统的变换域分析法进行模拟仿真,并对仿真实验结果进行合理分析,并得到有效的结论。
二、实验主要内容
1.对序列的产生和运算方法进行实现
2.序列的傅里叶变换实现、性质及分析
3.离散时间系统的Z域分析
4.信号时域采样及恢复
5.离散系统的Z域分析
6.创新训练拓展内容
三、实验主要仪器、设备及软件
1. 计算机
2. Matlab2014a以上版本
四、实验步骤、结果与分析(手写)
1.序列的基本运算
(1)产生余弦信号
x
(
n
)
=
c
o
s
(
0.04
π
n
)
x(n)=cos( 0.04πn)
x(n)=cos(0.04πn)及带噪信号
y
(
n
)
=
x
(
n
)
+
a
w
(
n
)
,
0
≤
n
≤
N
−
1
y(n)=x(n)+aw(n),0≤n≤N-1
y(n)=x(n)+aw(n),0≤n≤N−1(噪声采用randn函数,a及N自定)
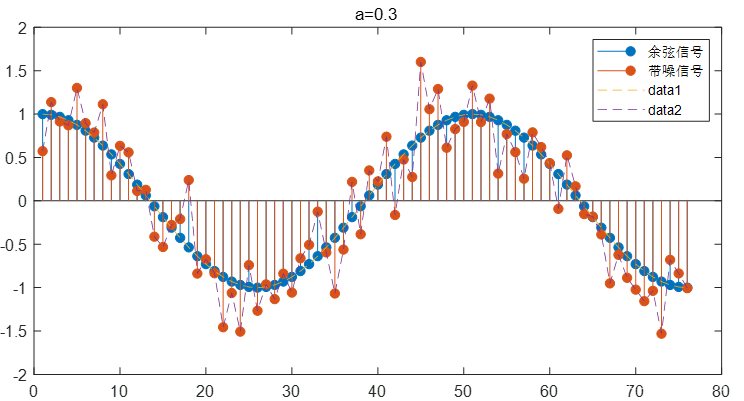
解:程序:
n=0:75;
x=cos(0.04*pi*n);
w=randn(1,76);
y=x+0.3*w;
stem(x,'filled');
hold on
stem(y,'filled')
legend('余弦信号','带噪信号')
hold on
plot(x,'--')
hold on
plot(y,'--')
title('a=0.3')
结果:
分析:
(2)已知
x
1
(
n
)
=
2
n
−
1
,
1
≤
n
≤
5
,
x
2
(
n
)
=
2
n
−
2
,
2
≤
n
≤
6
x_1 (n)=2n-1,1≤n≤5,x_2 (n)=2n-2, 2≤n≤6
x1(n)=2n−1,1≤n≤5,x2(n)=2n−2,2≤n≤6,求两个序列的和、乘积、序列x1的移位序列(移位方向及位数自定),序列x2的翻褶序列,画出原序列及运算结果图。
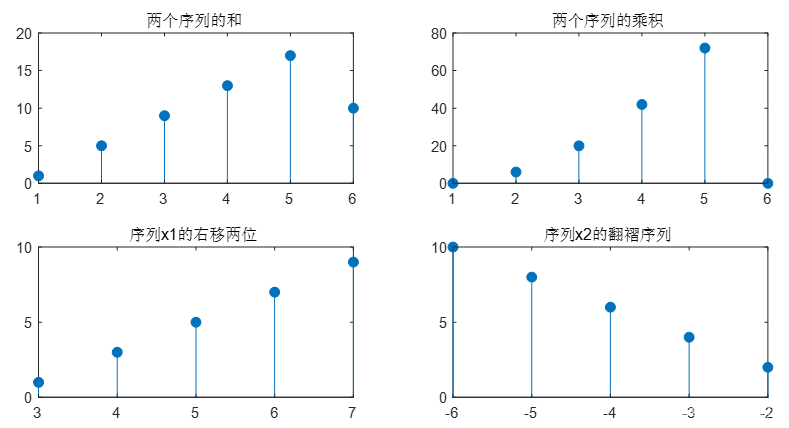
解:程序:
n1=1:5;
n2=2:6;
x1=2*n1-1;
x2=2*n2-2;
subplot(2,2,1)
[y1,n]=sigadd(x1,n1,x2,n2);
stem(n,y1,'filled')
title('两个序列的和')
subplot(2,2,2)
[y2,n]=sigmult(x1,n1,x2,n2);
stem(n,y2,'filled')
title('两个序列的乘积')
subplot(2,2,3)
[y3,n]=sigshift(x1,n1,2);
stem(n,y3,'filled')
title('序列x1的右移两位')
subplot(2,2,4)
[y4,n]=sigfold(x2,n2);
stem(n,y4,'filled')
title('序列x2的翻褶序列')
结果:
分析:
2. 序列的傅里叶变换
(1) 已知序列
x
(
n
)
=
(
0.5
)
n
u
(
n
)
x(n)=(0.5)^nu(n)
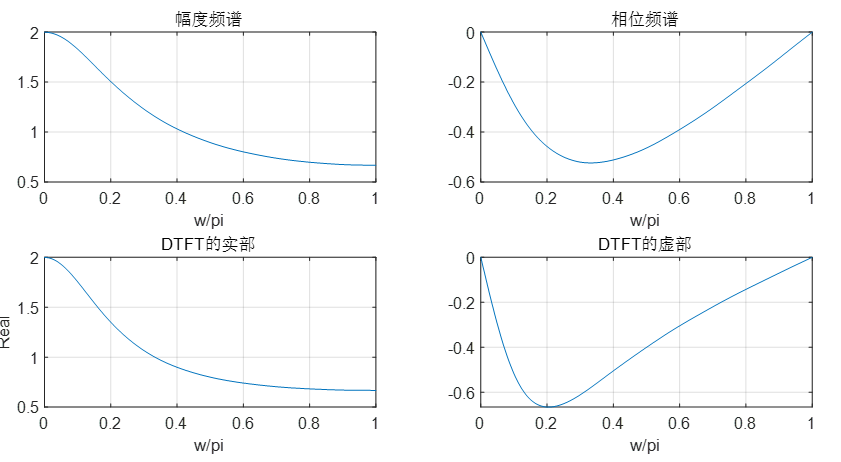
x(n)=(0.5)nu(n)。试求它的傅里叶变换,并且画出其幅度、相角、实部和虚部的波形,并分析其含有的频率分量主要位于高频区还是低频区。
解:程序:
n=0:10;
x=0.5.^(n);
w=[0:250]*pi/250;
X=x*exp(-j*n'*w);
subplot(2,2,1)
plot(w/pi,abs(X))
grid on
xlabel('w/pi')
title('幅度频谱')
subplot(2,2,2)
plot(w/pi,angle(X))
grid on
xlabel('frequency in pi units')
title('相位频谱')
xlabel('w/pi')
subplot(2,2,3)
plot(w/pi,real(X))
grid on
xlabel('w/pi')
title('DTFT的实部')
ylabel('Real')
subplot(2,2,4)
plot(w/pi,imag(X))
grid on
xlabel('w/pi')
title('DTFT的虚部')
结果:
分析:
(2)令模拟信号
x
a
(
t
)
=
e
(
−
1000
∣
t
∣
)
x_a (t)=e^{(-1000|t|)}
xa(t)=e(−1000∣t∣),求其傅立叶变换
X
a
(
j
Ω
)
X_a(jΩ)
Xa(jΩ),画出其幅度频谱。然后分别用fs=1kHz和fs=5kHz对其进行采样并离散化,求出离散时间信号的傅立叶变换
X
(
e
j
ω
)
X(e^{jω})
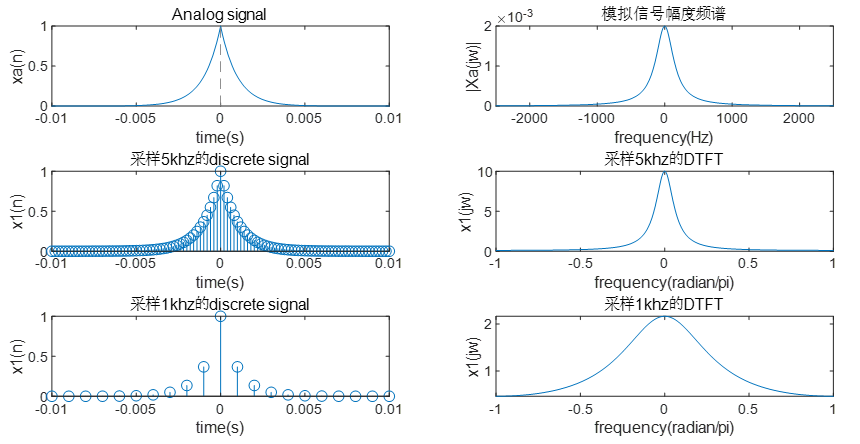
X(ejω),画出相应的幅度频谱,总结以上3个信号幅度频谱的联系与差异,并分析其原因。
解:程序:
clear;
syms f t;
xa=exp(-1000*abs(t));
Xa=2000/((2*pi*f)^2+1000^2);
subplot(3,2,1);
fplot(xa,[-0.01,0.01]);
axis([-0.01,0.01,0,1])
xlabel('time(s)');
ylabel('xa(n)');
title('Analog signal');
subplot(3,2,2);
fplot(abs(Xa),[-2500,2500])
xlabel('frequency(Hz)')
ylabel('|Xa(jw)|');
title('模拟信号幅度频谱');
%下面为采样频率5kHz时的程序
T=0.0002;
n=-50:1:50;
x=exp(-1000*abs(n*T));
K=500;k=0:1:K;w=pi*k/K;
X=x*exp(-j*n'*w);
X=real(X);
w=[-fliplr(w),w(2:K+1)];
X=[fliplr(X),X(2:K+1)];
subplot(3,2,3);
stem(n*T,x);
xlabel('time(s)');
ylabel('x1(n)');
title('采样5khz的discrete signal');
subplot(3,2,4);
plot(w/pi,X);
xlabel('frequency(radian/pi)');
ylabel('x1(jw)');title('采样5khz的DTFT');
%下面为采样频率5kHz时的程序
T=0.001;
n=-10:1:10;
x=exp(-1000*abs(n*T));
K=500;k=0:1:K;w=pi*k/K;
X=x*exp(-j*n'*w);
X=real(X);
w=[-fliplr(w),w(2:K+1)];
X=[fliplr(X),X(2:K+1)];
subplot(3,2,5);
stem(n*T,x);
xlabel('time(s)');
ylabel('x1(n)');
title('采样1khz的discrete signal');
subplot(3,2,6);
plot(w/pi,X);
xlabel('frequency(radian/pi)');
ylabel('x1(jw)');title('采样1khz的DTFT');
结果:
分析:
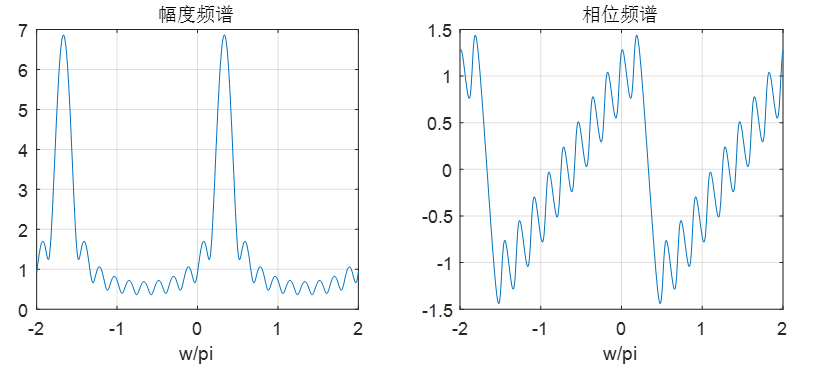
3. 序列的傅里叶变换性质分析
(1)已知序列x(n)=
(
0.9
e
j
π
/
3
)
n
(0.9e^{jπ/3})^n
(0.9ejπ/3)n,0≤n≤10,求其傅里叶变换,并讨论其傅里叶变换的周期性和对称性。
解:程序:
n=0:10;
x=(0.9*exp(j*pi/3)).^(n);
w=[-500:500]*pi/250;
X=x*exp(-j*n'*w);
subplot(1,2,1)
plot(w/pi,abs(X))
grid on
xlabel('w/pi')
title('幅度频谱')
subplot(1,2,2)
plot(w/pi,angle(X))
grid on
xlabel('frequency in pi units')
title('相位频谱')
xlabel('w/pi')
结果:
分析:
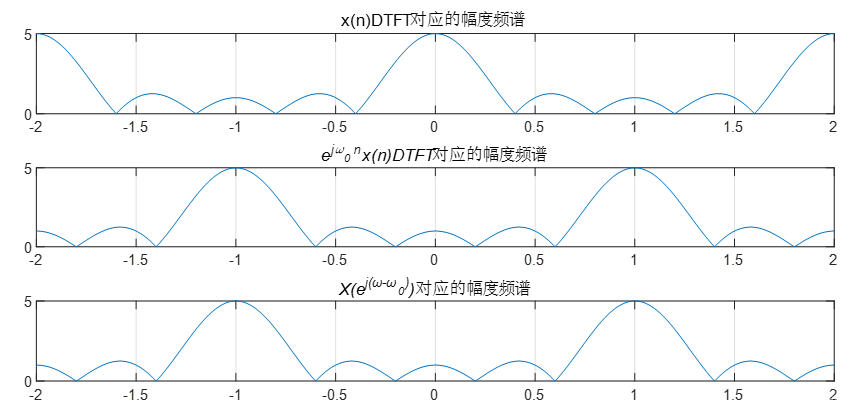
(2)编写程序验证序列傅里叶变换频移性质,时域卷积定理(时域卷积后的频域特性)。(所需信号自定)
频移(调制):
F
T
[
e
j
ω
0
n
x
(
n
)
]
=
X
(
e
j
(
ω
−
ω
0
)
)
FT[ e^{jω_0n}x(n)]=X(e^{j(ω-ω_0)})
FT[ejω0nx(n)]=X(ej(ω−ω0))
解:程序:
n=0:4;
x1=(1).^n;
x2=((1).^n).*exp(i*pi*n);
w=[-500:500]*pi/250;
X1=x1*exp(-j*n'*w);
X2=x2*exp(-j*n'*w);
w1=[-250:750]*pi/250;
X3=x1*exp(-j*n'*w1);
subplot(3,1,1);
plot(w/pi,abs(X1))
title('x(n)DTFT对应的幅度频谱');
grid on
subplot(3,1,2);
plot(w/pi,abs(X2))
title('\ite^{j{\omega}_0 n}x(n)DTFT对应的幅度频谱');
grid on
subplot(3,1,3);
plot((w1-pi)/pi,abs(X3))
title('\itX(e^{j(ω-ω_0)})对应的幅度频谱');
grid on
结果:
分析:
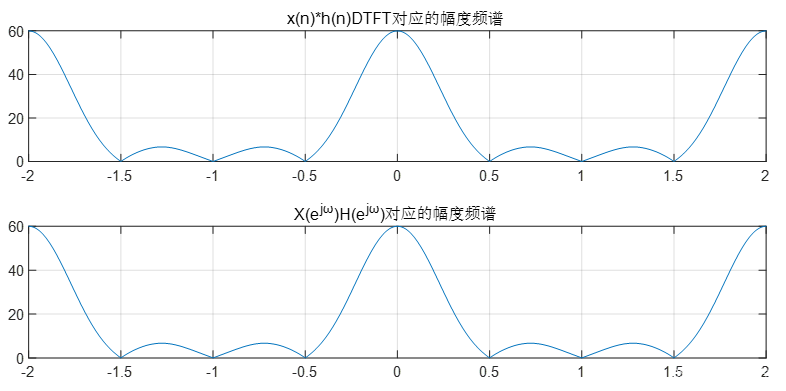
时域卷积定理:若 y ( n ) = x ( n ) ∗ h ( n ) ,则 Y ( e j ω ) = X ( e j ω ) H ( e j ω ) y(n)=x(n)*h(n),则 Y(e^{jω})=X(e^{jω})H(e^{jω}) y(n)=x(n)∗h(n),则Y(ejω)=X(ejω)H(ejω)
程序:
n=0:3;
n1=0:6
x1=(1).^n;
x2=(2).^n;
y=conv(x1,x2)
w=[-500:500]*pi/250;
Y1=y*exp(-j*n1'*w);
X1=x1*exp(-j*n'*w);
X2=x2*exp(-j*n'*w);
Y2=X1.*X2;
subplot(2,1,1);
plot(w/pi,abs(Y1))
title('x(n)*h(n)DTFT对应的幅度频谱');
grid on
subplot(2,1,2);
plot(w/pi,abs(Y2))
title('X(e^{jω})H(e^{jω})对应的幅度频谱');
grid on
结果:
分析:
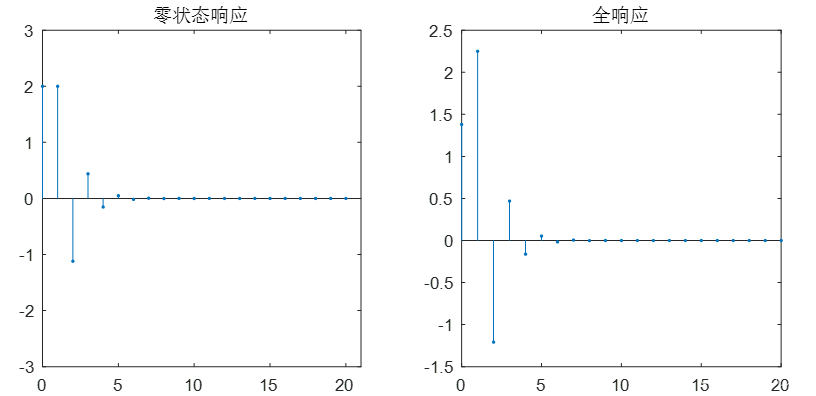
4. 时域差分方程的求解
求解差分方程
y
(
n
)
+
a
1
y
(
n
−
1
)
+
a
2
y
(
n
−
2
)
=
b
0
x
(
n
)
+
b
1
x
(
n
−
1
)
y(n)+a_1 y(n-1)+a_2 y(n-2)=b_0 x(n)+b_1x(n-1)
y(n)+a1y(n−1)+a2y(n−2)=b0x(n)+b1x(n−1)的零状态响应和全响应。已知x(n)为单位取样序列,
y
(
−
1
)
=
1
,
y
(
−
2
)
=
2
,
a
1
=
0.5
,
a
2
=
0.06
,
b
0
=
2
,
b
1
=
3
y(-1)=1,y(-2)=2,a_1=0.5,a_2=0.06,b_0=2,b_1=3
y(−1)=1,y(−2)=2,a1=0.5,a2=0.06,b0=2,b1=3。
解:程序:
xn=[1 zeros(1,20)];
B=[2,3];
A=[1,0.5,0.06];
ys=[1,2];
xi=filtic(B,A,ys);
yn1=filter(B,A,xn);
yn2=filter(B,A,xn,xi);
subplot(1,2,1)
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
axis([0,21,-3,3]);
title('零状态响应')
subplot(1,2,2)
n2=0:length(yn2)-1;
stem(n2,yn2,'.')
title('全响应')
结果:
分析:
5. 离散系统的Z域分析
(1)利用系统函数H(z)分析系统的稳定性。假设系统函数如下式:
H
(
z
)
=
(
z
+
9
)
(
z
−
3
)
3
z
4
−
3.98
z
3
+
1.17
z
2
+
2.3418
z
−
1.5147
H(z)=\frac{(z+9)(z-3)}{3z^4-3.98z^3+1.17z^2+2.3418z-1.5147}
H(z)=3z4−3.98z3+1.17z2+2.3418z−1.5147(z+9)(z−3)
解:程序:
A=[3,-3.98, 1.17, 2.3418,-1.5147];
p=roots(A)
pm=abs(p);
if max(pm)<1 disp('系统因果稳定'),else,
disp('系统不因果稳定'), end
结果:
p = -0.7486 + 0.0000i
0.6996 + 0.7129i
0.6996 - 0.7129i
0.6760 + 0.0000i
分析:
(2) 已知线性时不变系统的系统函数:
H
(
z
)
=
0.1
+
0.3
z
−
1
1
−
0.4
z
−
1
+
0.8
z
−
2
H(z)=\frac{0.1+0.3z^{-1}}{1-0.4z^{-1}+0.8z^{-2}}
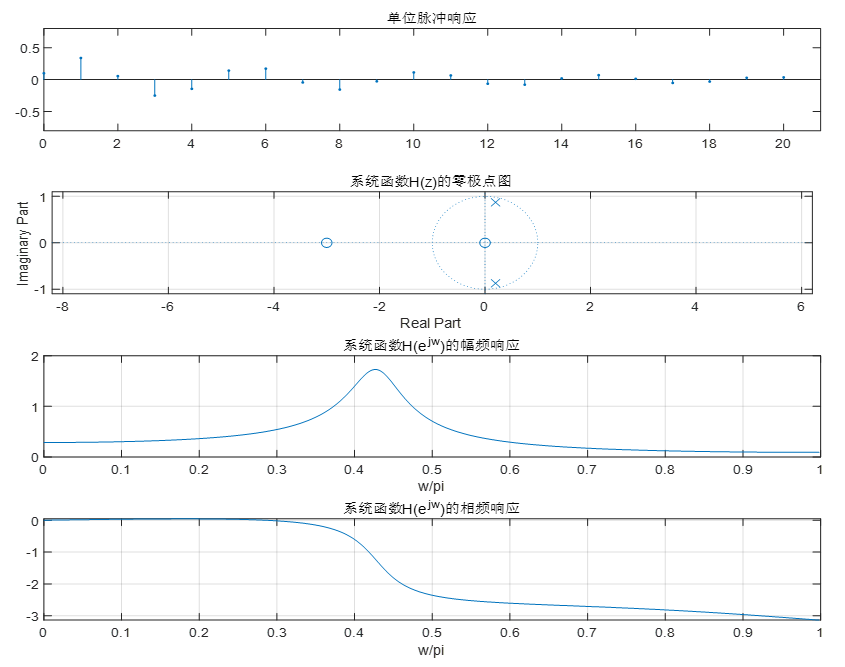
H(z)=1−0.4z−1+0.8z−20.1+0.3z−1编写程序求其单位脉冲响应,频率响应及系统零极点,并画出相应图形(其中频率响应需分别画出幅频响应和相频响应),根据零极点图和幅频响应曲线,分析系统函数零极点对系统幅频响应的影响。
解:程序:
B=[0.1 0.3];
A=[1 -0.4 0.8];
subplot(4,1,1);
xn=[1 zeros(1,20)];
yn1=filter(B,A,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
title('单位脉冲响应')
axis([0,21,-0.8,0.8]);
subplot(4,1,2);
zplane(B,A);
title('系统函数H(z)的零极点图')
grid on
subplot(4,1,3);
[H,w]=freqz(B,A);
plot(w/pi,abs(H))
title('系统函数H(e^{jw})的幅频响应')
xlabel('w/pi');
grid on
subplot(4,1,4);
[H,w]=freqz(B,A);
plot(w/pi,angle(H))
title('系统函数H(e^{jw})的相频响应')
xlabel('w/pi');
grid on
结果:
分析:
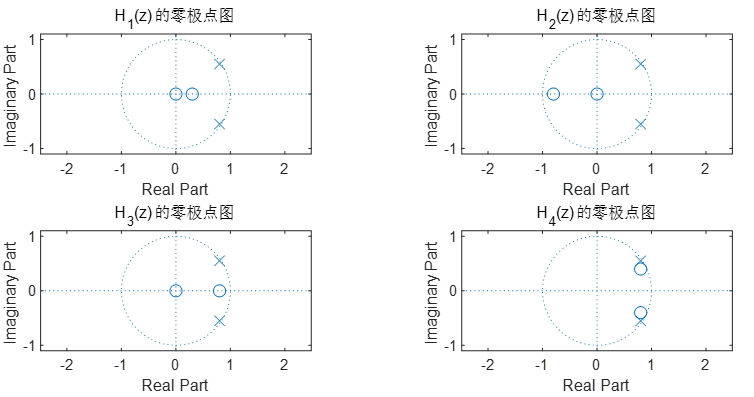
(3) 下面四个二阶网络的系统函数具有一样的极点分布:
1
)
H
1
(
z
)
1
−
0.3
z
−
1
(
1
−
1.6
z
−
1
+
0.9425
z
−
2
1)H_1 (z)\frac{1-0.3z^{-1}}{(1-1.6z^{-1}+0.9425z^{-2}}
1)H1(z)(1−1.6z−1+0.9425z−21−0.3z−1
2
)
H
2
(
z
)
=
1
+
0.8
z
−
1
1
−
1.6
z
−
1
+
0.9425
z
−
2
2)H_2 (z)=\frac{1+0.8z^{-1}}{1-1.6z^{-1}+0.9425z^{-2}}
2)H2(z)=1−1.6z−1+0.9425z−21+0.8z−1
3
)
H
3
(
z
)
=
1
−
0.8
z
−
1
1
−
1.6
z
−
1
+
0.9425
z
−
2
3)H_3 (z)=\frac{1-0.8z^{-1}}{1-1.6z^{-1}+0.9425z^{-2}}
3)H3(z)=1−1.6z−1+0.9425z−21−0.8z−1
4
)
H
4
(
z
)
=
1
−
1.6
z
−
1
+
0.8
z
−
2
1
−
1.6
z
−
1
+
0.9425
z
−
2
4)H_4 (z)=\frac{1-1.6z^{-1}+0.8z^{-2}}{1-1.6z^{-1}+0.9425z^{-2}}
4)H4(z)=1−1.6z−1+0.9425z−21−1.6z−1+0.8z−2
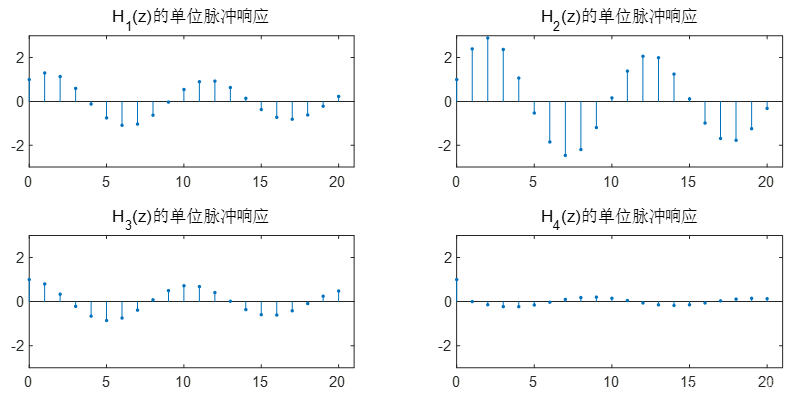
请分析研究零点分布对于单位脉冲响应的影响。要求:
1)分别画出各系统的零、 极点分布图;
2)分别求出各系统的单位脉冲响应,并画出其波形;
3)分析零点分布对于单位脉冲响应的影响。
解:1)程序:
subplot(2,2,1)
b=[1,-0.3];
a=[1,-1.6,0.9425];
zplane(b,a)
title('H_1(z)的零极点图')
subplot(2,2,2)
b=[1,0.8];
a=[1,-1.6,0.9425];
zplane(b,a)
title('H_2(z)的零极点图')
subplot(2,2,3)
b=[1,-0.8];
a=[1,-1.6,0.9425];
zplane(b,a)
title('H_3(z)的零极点图')
subplot(2,2,4)
b=[1,-1.6,0.8];
a=[1,-1.6,0.9425];
zplane(b,a)
title('H_4(z)的零极点图')
结果:
2)程序:
subplot(2,2,1)
xn=[1 zeros(1,20)];
B=[1,-0.3];
A=[1,-1.6,0.9425];
yn1=filter(B,A,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
axis([0,21,-3,3]);
title('H_1(z)的单位脉冲响应')
subplot(2,2,2)
B=[1,0.8];
A=[1,-1.6,0.9425];
yn1=filter(B,A,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
axis([0,21,-3,3]);
title('H_2(z)的单位脉冲响应')
subplot(2,2,3)
B=[1,-0.8];
A=[1,-1.6,0.9425];
yn1=filter(B,A,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
axis([0,21,-3,3]);
title('H_3(z)的单位脉冲响应')
subplot(2,2,4)
B=[1,-1.6,0.8];
A=[1,-1.6,0.9425];
yn1=filter(B,A,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
axis([0,21,-3,3]);
title('H_4(z)的单位脉冲响应')
结果:
分析:
6. 创新训练拓展内容
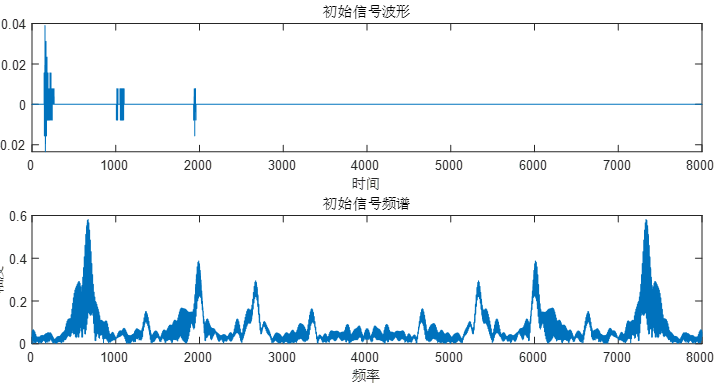
(1)利用Matlab自带的录音功能,或利用Goldwave等音频编辑软件,对语音或其他音频信号进行采集并保存为*.wav文件。
要求:1)采用不同的采样频率(2000Hz,4000Hz,8000Hz,16000Hz等)。
2)对采集得到的信号进行播放,并画图。
3)分析在不同采样频率下得到的信号有何不同。
解:程序: %仅以2000hz采样频率为例
nChannels=1;
Fs=2000;
nBits=8;
recObj=audiorecorder(Fs,nBits,nChannels);
disp('Start speaking.')
recordblocking(recObj, 4);
disp('End of Recording.');
play(recObj);% 回放录音数据
y = getaudiodata(recObj);
subplot(2,1,1);
plot(y);
xlabel('时间');
ylabel('幅度');
title('初始信号波形');
subplot(2,1,2); %绘出频域频谱
plot(abs(fft(y)));
title('初始信号频谱');
xlabel('频率');
ylabel('幅度');
Start speaking.
End of Recording.
结果:
(2)设定一个连续时间信号,进行时域采样和恢复(信号的恢复,采用内插公式实现,见实验原理或者教材式(1.5.9)),要求分析不同采样频率(要求至少分别讨论有混叠和无混叠两种情况)对恢复结果的影响,给出实验程序及各关键步骤图形结果。
解:设定连续时间信号为:
f
=
c
o
s
(
2000
∗
t
∗
p
i
)
+
c
o
s
(
1000
∗
t
∗
p
i
)
f=cos(2000*t*pi)+cos(1000*t*pi)
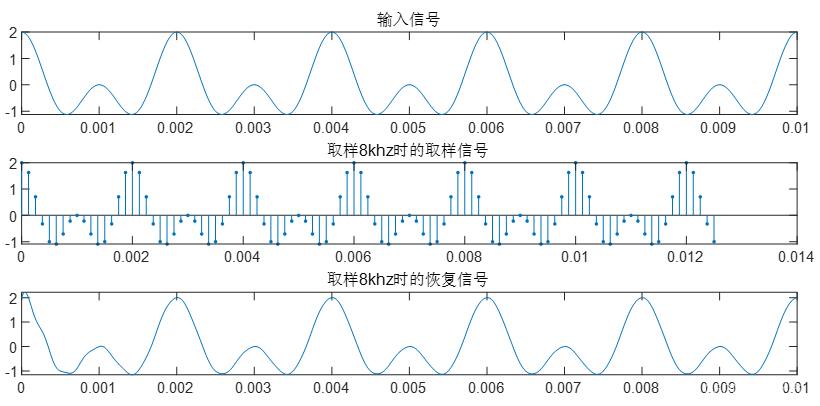
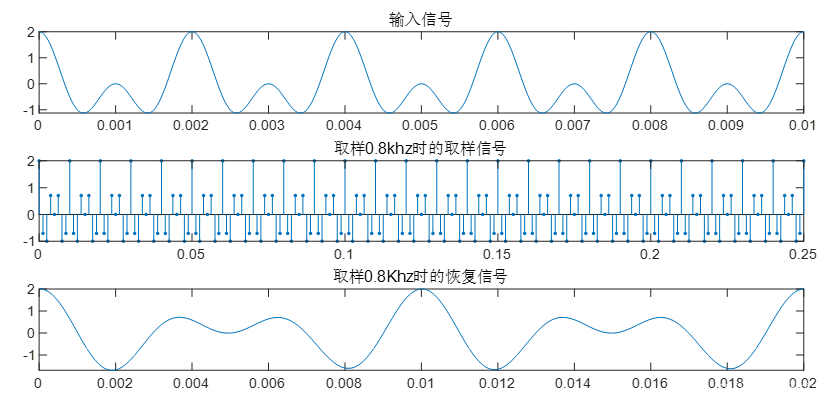
f=cos(2000∗t∗pi)+cos(1000∗t∗pi),分别采用8000hz无混叠和800hz有混叠进行取样,如下所示:
程序:
subplot(3,1,1);
t=0:0.00001:0.01;
f=cos(2000*t*pi)+cos(1000*t*pi);
plot(t,f)
title('输入信号');
T=1/8000;
n=0:100;
x=cos(2000*pi*n*T)+cos(1000*pi*n*T);
t=0:0.000001:0.01;
f0=x*((sin(pi*(t-n'*T)/T))./(pi*(t-n'*T)/T));
subplot(3,1,2);
stem(n*T,x,'.')
title('取样8khz时的取样信号');
subplot(3,1,3);
plot(t,f0)
title('取样8khz时的恢复信号');
结果:
程序:
subplot(3,1,1);
t=0:0.00001:0.01;
f=cos(2000*t*pi)+cos(1000*t*pi);
plot(t,f)
title('输入信号');
T=1/800;
n=0:200;
x=cos(2000*pi*n*T)+cos(1000*pi*n*T);
t=0:0.00001:0.02;
f1=x*((sin(pi*(t-n'*T)/T))./(pi*(t-n'*T)/T));
subplot(3,1,2);
stem(n*T,x,'.')
title('取样0.8khz时的取样信号');
subplot(3,1,3);
plot(t,f1)
title('取样0.8Khz时的恢复信号');
结果:
分析:
(3)设计一个离散系统,给出系统函数或差分方程,设定激励及初始条件。要求:
1)系统因果稳定,绘制系统函数零极点图。
2)求单位脉冲响应h(n);
3)求系统零输入响应及零状态响应,要求零状态响应采样三种方法求解(卷积的方法、迭代解法、变换域求解方法),激励自定;
4)分析系统频响特性,画出频响函数幅频曲线和相频曲线。
解:设定差分方程:
y
(
n
)
−
1.3
y
(
n
−
1
)
+
0.4
y
(
n
−
2
)
=
x
(
n
)
−
x
(
n
−
1
)
y(n)-1.3y(n-1)+0.4y(n-2)=x(n)-x(n-1)
y(n)−1.3y(n−1)+0.4y(n−2)=x(n)−x(n−1),激励为
x
(
n
)
=
ε
(
k
)
x(n)=ε(k)
x(n)=ε(k),初始条件为
y
(
−
1
)
=
1
,
y
(
−
2
)
=
2
y(-1)=1,y(-2)=2
y(−1)=1,y(−2)=2。故离散系统为
H
(
z
)
=
(
z
(
z
−
1
)
(
z
−
0.5
)
(
z
−
0.8
)
H(z)=\frac{(z(z-1)}{(z-0.5)(z-0.8)}
H(z)=(z−0.5)(z−0.8)(z(z−1)。
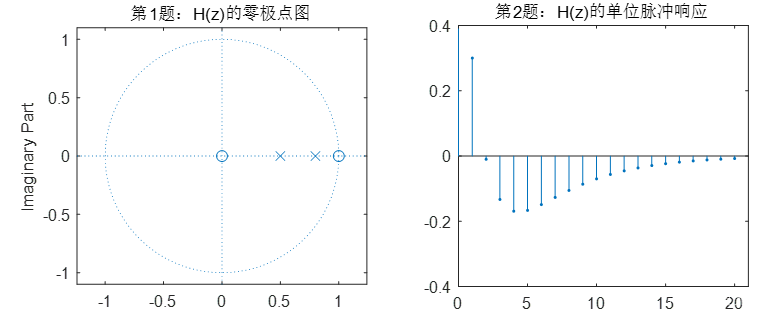
1)2)两小问的程序:
b=[1,-1];
a=[1,-1.3,0.4];
subplot(1,2,1);
zplane(b,a)
title('第1题:H(z)的零极点图')
subplot(1,2,2);
xn=[1 zeros(1,20)];
yn1=filter(b,a,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
axis([0,21,-0.4,0.4]);
title('第2题:H(z)的单位脉冲响应')
结果:
3)程序:
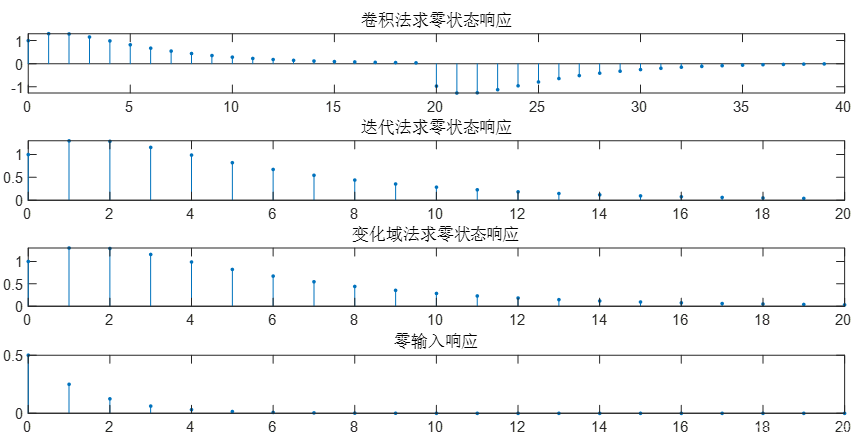
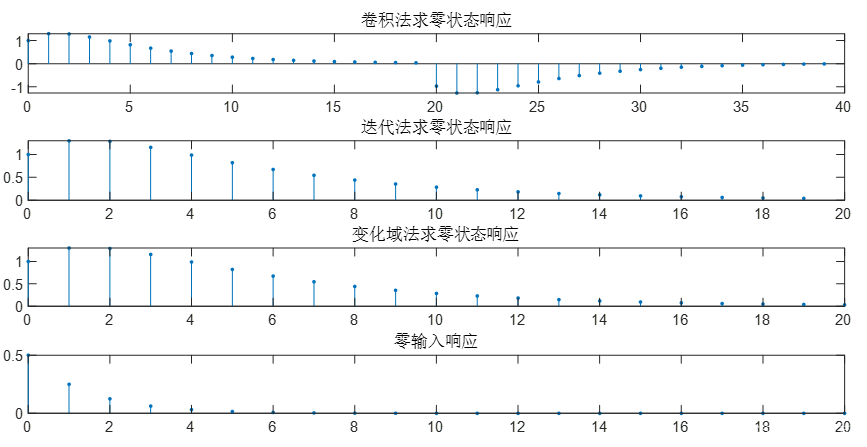
subplot(4,1,1)
n=0:20;
h=(5*(1/2).^n)/3 - (2*(4/5).^n)/3;
h1=ones(1,20);
y=conv(h,h1);
stem(0:39,y,'.')
title('卷积法求零状态响应')
subplot(4,1,2)
b=[1,-1];
a=[1,-1.3,0.4];
xn=ones(1,20);
yn1=filter(b,a,xn);
n1=0:length(yn1)-1;
stem(n1,yn1,'.')
title('迭代法求零状态响应')
subplot(4,1,3)
n=0:20;
y=(8*(4/5).^n)/3 - (5*(1/2).^n)/3;
stem(n,y,'.')
title('变化域法求零状态响应')
subplot(4,1,4)
xn=[1 zeros(1,20)];
b=[1,-1];
a=[1,-1.3,0.4];
ys=[1,2];
xi=filtic(b,a,ys);
yn1=filter(b,a,xn);
yn2=filter(b,a,xn,xi);
n2=0:length(yn2)-1;
stem(n2,yn2-yn1,'.')
title('零输入响应')
结果:
4)程序:
B=[1,-1];
A=[1,-1.3,0.4];
subplot(1,2,1);
[H,w]=freqz(B,A);
plot(w/pi,abs(H))
title('系统函数H(e^{jw})的幅频响应')
xlabel('w/pi');
grid on
subplot(1,2,2);
[H,w]=freqz(B,A);
plot(w/pi,angle(H))
title('系统函数H(e^{jw})的相频响应')
xlabel('w/pi');
grid on
结果:
分析: