链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。
链表的特点:
- 存储空间可连续也可不连续
- 链表的存取通过头节点开始
- 是非随机存取的存储结构
链表节点的结构:

整个链表的结构 :

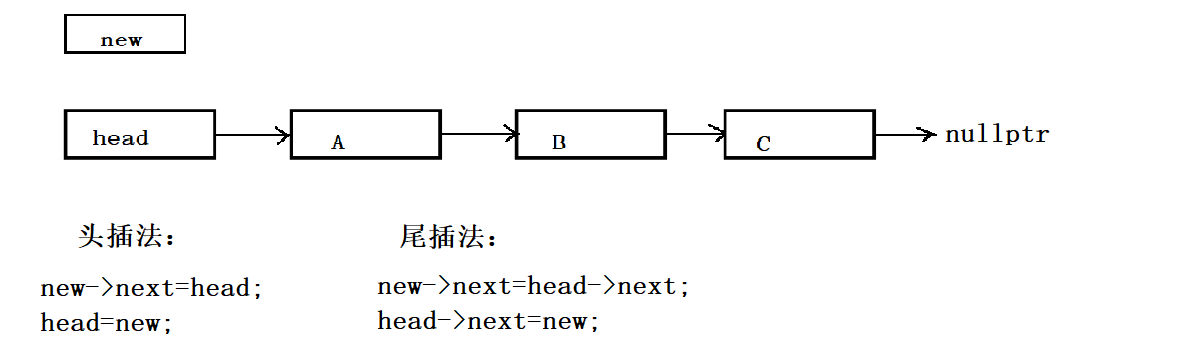
链表的插入方式有两种:
- 头插法:
- 尾插法:
单链表结构为:
template<class T>
class list;
template<class T>
class listNode
{
friend class list<T>;
private:
T _elem;//数据
listNode<T>* next;//下一个节点
public:
listNode(T a=0) :_elem(a) : next(nullptr);
};
template<class T>
class list
{
private:
listNode* top;//头节点指针
int length;//链表长度
};以下为功能的实现:
头部插入:

template<class T>
void list<T>::head_insert(T const a)//头部插入
{
listNode<T>* p = new listNode(a);//创建一个新节点
//尾插法
p->next = top->next;//p的下一个节点指向头节点的下一个节点
top->next = p;//头节点的下一个节点为p
length++;
}尾部插入

template<class T>
void list<T>::tail_insert(T const a)//尾部插入
{
listNode<T>* p = new listNode(a);//创建一个新节点
listNode<T>* q;
q = top;
int i = length;
while (i>0)//找到链表最后一个节点
{
q = q->next;
--i;
}
q->next = p;//最后节点连接新节点
}
删除节点
template<class T>
void list<T>::delete_elem(int i)//删除节点
{
if (i > length || i <= 0 || empty()) return;
listNode<T>* p,q;
p = top;
int n = length;
while (n-1 > 0)
{
p = p->next;
}
q = p->next;
p->next = q->next;
delete q;//清空数据
--length;//个数-1
}单链表循环链表:
- 循环链表是与单链表一样,是一种链式存储结构,所不同的是,循环链表的最后一个结点的指针是指向该循环链表的第一个结点或者表头结点,从而构成一个环形的链。
- 在判断是否到表尾时,是判断该结点链域的值是否是表头结点,当链域值等于表头指针时,说明已到表尾。


双向链表:(重点)
在双向链表中,结点除含有数据域外,还有两个链域,一个存储直接后继结点地址,一般称之为右链域;一个存储直接前驱结点地址,一般称之为左链域。
节点结构为:

双向链表结构为:

template<class T>
class list;
template<class T>
class listnode
{
friend class list<T>;
private:
T elem;//数据
listnode<T>* prior;//前驱
listnode<T>* next;//后继
public:
listnode(T const a=0) :elem(a) : prior(nullptr) : next(nullptr);
};
template<class T>
class list
{
private:
listnode<T>* top;//头节点
int length;//记录数据个数
public:
list()
{
top = new listnode<T>;
length = 0;
}
};以下为功能的实现:
插入:

listnode<T>* s=new listnode<T>(x);
s->prior=p->prior;
p->prior->next=s;
s->next=b;
p->prior=s;
删除:

p->prior->next=p->next;
p->next->prior=p->prior;双向循环链表:

链表的一些操作:
1.反转单链表
class Solution {
public:
ListNode* ReverseList(ListNode* pHead) {
ListNode* p=nullptr;//存入next指针的指向
ListNode* H=pHead;//p反转的节点
while(H)//当H不为nullptr
{
ListNode* next=H->next;//next指向下一个要反转的节点
H->next=p;//H的next指向p
p=H;//p存放现在这个节点,应为下一个节点的next为H
H=next;//指向next,
}
return p;//当H为nullptr,p刚好指向最后一个节点,变为头结点
}
};2.判断单链表是否有环
判断方法为:快慢指针,一个慢一个快,如果有环的话,这两个指针迟早会相遇。
限制条件:主要限制快指针不为nullptr
class Solution {
public:
bool hasCycle(ListNode *head) {
if(head==nullptr)return false;//空链表返回false
ListNode* p=head;//慢指针
ListNode* p1=head;//快指针
while(p1!=nullptr && p1->next!=nullptr)
{
p=p->next;
p1=p1->next->next;
if(p==p1)
{
return true;
}
}
return false;
}
};3.查找环的入口节点
首先先判断是否有环,有环的话进行下一步操作。
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
ListNode* newlist=nullptr;
ListNode*n=pHead;//慢指针
ListNode*m=pHead;//快指针
ListNode*k=pHead;//首指针
if(pHead==nullptr) return newlist;//空链表返回null
while(m!=nullptr && m->next!=nullptr)//判断是否有环
{
n=n->next;
m=m->next->next;
if(m==n)//有环的话
{
while(k!=n)//当两个指针相遇
{
k=k->next;
n=n->next;
}
newlist=k;
break;
}
}
return newlist;
}
};