manim学习笔记04：使用manim，表示向量和加法。

一，相关定义

1.有向线段：

规定若线段 AB的端点为起点为A，B为终点，则线段就具有了从起点 A到终点 B的方向和长度。具有方向和长度的线段叫做有向线段。

接下来我们体会一下相关的代码：

class VectorArrow(Scene):
    def construct(self):
        colorA = "#87c2a5"
        colorB = "#525893"
        colorC = "#e07a5f"
        dot = Dot(ORIGIN,color=RED)
        self.camera.background_color = WHITE
        arrow01 = Arrow(dot, [2, 1.2, 0], buff=0,color=colorA)
        arrow02 = Arrow(dot, [3.5, 1, 0], buff=0,color=colorB)
        arrow03 = Arrow(dot, [3, 3.4, 0], buff=0,color=colorC)
        arrow04 = Arrow(dot, [-2, 4, 0], buff=0,color=colorA)
        arrow05 = Arrow(dot, [-3.5, 1, 0], buff=0,color=colorB)
        arrow06 = Arrow(dot, [-0.6, 3.4, 0], buff=0,color=colorC)
        arrow07 = Arrow(dot, [2, -4, 0], buff=0,color=colorA)
        arrow08 = Arrow(dot, [3.5, -1, 0], buff=0,color=colorB)
        arrow09 = Arrow(dot, [0.6, -3.4, 0], buff=0,color=colorC)
        arrow10 = Arrow(dot, [-2, -3, 0], buff=0,color=colorA)
        arrow11 = Arrow(dot, [-3.5, -1, 0], buff=0,color=colorB)
        arrow12 = Arrow(dot, [-3, -3.4, 0], buff=0,color=colorC)
        
        
        #numberplane = NumberPlane()
        #origin_text = Text('(0, 0)').next_to(dot, DOWN)
        #tip_text = Text('(2, 2)').next_to(arrow.get_end(), RIGHT)
        self.add(dot,arrow01,arrow02,arrow03,arrow04,arrow05,arrow06,arrow07,
                    arrow08,arrow09,arrow10,arrow11,arrow12)

结果如下：

2.向量的模

向量的大小，也就是向量的长度(或称模)。向量a的模记作|a|。向量的模是非负实数，向量的模是可以比较大小的。如向量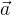的起点为远点，重点为（x,y）,则|a|=。

可视化代码为：

from manim import *

class VectorArrow03(Scene):
    def construct(self):
        dot = Dot(ORIGIN)
        arrow = Arrow(dot, [2, 2, 0], buff=0)
        numberplane = NumberPlane()
        t0 = MathTex(r"\begin{bmatrix}0\\0\end{bmatrix}")
        t1= MathTex(r"\begin{bmatrix}X(2)\\Y(2)\end{bmatrix}")
        t2=MathTex(r"\begin{bmatrix}0 & 0 \\ 2 & 2\end{bmatrix}")
        t3=MathTex(r"\overrightarrow{a}") 
        vec=t2.next_to([1,2,0],UP)
        origin_text = t0.next_to(dot, LEFT+DOWN)
        tip_text = t1.next_to(arrow.get_end(), RIGHT+DOWN)
        tip_text01 = t3.next_to(arrow.get_end(),3*LEFT+DOWN)
        AA=MathTex(r"\left | \overrightarrow{a}  \right | =\sqrt{x^{2}+y^{2} } ")
        t4=AA.next_to([5,-1,0],3*LEFT+DOWN)
        
        
        self.add(numberplane,t2,t4, dot,vec, arrow, origin_text, tip_text,tip_text01)
%manim -qm -v WARNING VectorArrow03

结果为：

 3.向量的加法：

可视化代码为：

from manim import *

class ParallelogramRule(Scene):
    def construct(self):
        numberplane = NumberPlane()
        dot = Dot(ORIGIN)
        # Create vectors
        vec_a = Arrow(start=dot, end=[2, 1, 0],buff=0,  color=BLUE)
        vec_b = Arrow(start=dot, end=[1, 2, 0],buff=0, color=RED)

        # Create parallelogram
        parallelogram = Polygon(ORIGIN, vec_a.get_end(), vec_a.get_end() + vec_b.get_end(), vec_b.get_end(), color=GREEN, fill_color=GREEN, fill_opacity=0.5)
        self.add(numberplane,dot)
        # Display vectors and parallelogram
        self.play(Create(vec_a), Create(vec_b))
        self.play(Create(parallelogram))

        self.wait(1)

class TriangleRule(Scene):
    def construct(self):
        # Create vectors
        numberplane = NumberPlane()
        dot = Dot(ORIGIN)
        vec_a = Arrow(start=ORIGIN, end=[2, 1, 0],buff=0 ,color=BLUE)
        vec_b = Arrow(start=ORIGIN, end=[1, 2, 0],buff=0, color=RED)

        # Create triangle
        triangle = Polygon(ORIGIN, vec_a.get_end(), vec_a.get_end() + vec_b.get_end(), color=PURPLE)
        self.add(numberplane,dot)
        # Display vectors and triangle
        self.play(Create(vec_a), Create(vec_b))
        self.play(Create(triangle))

        self.wait(1)

 运行结果为：