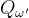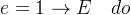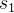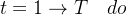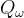第7章 DQN算法

7.1简介

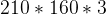
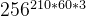
Q-learning算法，是以矩阵的方式建立一张存储每个状态下所有动作Q值的表格。表格中的每一个动作Q(s,a)表示在状态s下选择动作a然后继续遵循某一策略预期能够得到的期望回报。但是，这种用表格存储动作价值的做法只在环境的状态和动作都是离散，且空间比较小的情况下适用，我们之前进行代码施展的几个环境都是如此（如悬崖漫步）。当状态或者动作数量非常巨大的时候，这种做法就不适用。例如，当状态是一张RGB图像时，假设图像大小为 210*160*3 ，此时一共有 $256^{210*60*3}$ 种状态，在计算机中存储这个数量级的Q值表格是不现实的。更甚者，当状态或者动作连续的时候，就会有无限个状态动作对，更加无法使用表格的形式来记录各个状态动作对的Q值。

7.2 CartPole环境

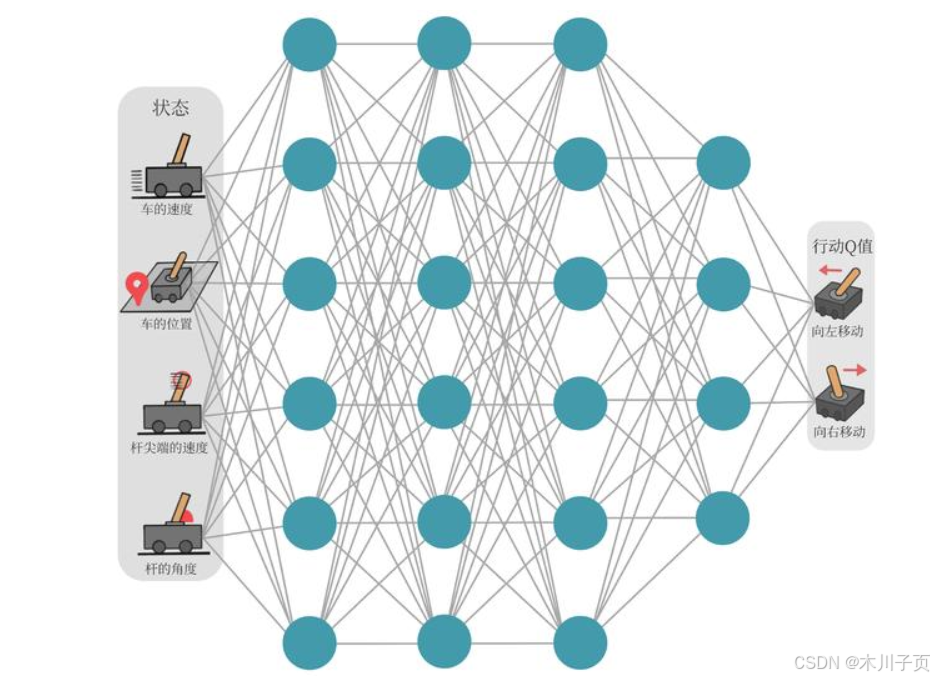
以下图所示的所示的CartPole环境为例，它的状态值就是连续的，动作值是离散的。

在车杆环境中，有一辆小车，只能提的任务是通过左右移动保持车上的杆竖直，若杆的倾斜度数过大，或者坚持时间到达200帧，则游戏结束。智能体的状态是一个维数为4的向量，每一维都是连续的，其动作是离散的，动作空间大小为2，详细如下面两个表所示。在游戏中每坚持一帧，智能体获得分数为1的奖励，坚持时间越长，则最后的分数越高，坚持200帧即可获得最高分数。

表1 CartPole环境的状态空间
维度	意义	最小值	最大值
0	车的位置	-2.4	2.4
1	车的速度	-Inf	Inf
2	杆的角度	~-41.8°	~41.8°
3	杆尖端的速度	-Inf	Inf

表2 CartPole环境的动作空间
标号	动作
0	向左移动小车
1	向右移动小车

7.3DQN

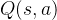
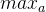
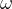
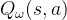
现在我们想在类似车杆的环境中得到动作价值函数 Q(s,a) ,由于状态每一维度的值都是连续的，无法使用表格记录，因此一个常见的解决方法表示使用函数拟合的思想。由于神经网络具有强大的表达能力，因此我们可以用一个神经网络来表示函数Q。若动作是连续（无限）的，神经网络的输入是状态s和动作a，然后输出一个标量，表示在状态s下采取动作a能获得的价值。若动作是离散（有限）的，除了可以采取动作连续情况下的做法，我们还可以只将状态s输入到神经网络中，使其同时输出每一个动作的Q值。通常DQN以及Q-learning只能处理动作离散的情况，因为在函数Q的更新过程中有 max_a 这一操作。假设神经网络用来拟合函数 $\omega$ 的参数是，即每一个状态s下所有动作a的Q值我们都能表示为 $Q_{\omega}(s,a)$ .我们将用于拟合函数Q函数的神经网络称为Q网络。如下图所示：

那么Q网络的损失函数是什么呢？我们先回顾一下Q-learning的更新规则：

$Q(s,a) \leftarrow Q(s,a) + \alpha[r + \gamma max_{a' \in A}(s',a') - Q(s,a)]$

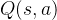
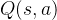
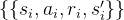
上述公式用时序差分学习目标 $r + \gamma max_{a' \in A}Q(s', a')$ 来增量式更新 Q(s,a) ,也就是说要使 Q(s,a) 和TD目标 $r + \gamma max_{a' \in A} Q(s', a')$ 靠近。于是，对于一组数据 $\{\{ s_i, a_i, r_i, s_i'\}\}$ ,我们可以很自然地将Q网络的损失函数构造成为均方误差的形式：

$\omega^* = argmin_{\omega} \frac{1}{2N} \sum_{i=1}^N [Q_\omega (s_i, a_i) - (r_i + \gamma max_{a'} Q_\omega (s_i', a'))]^2$

至此，我们就可以将Q-learning扩展到神经网络形式-深度Q网络算法。由于DQN是离线策略算法，因此我们在收集数据的时候可以使用一个 $\epsilon$ -贪婪策略来平衡探索和利用，将收集到的数据储存起来，在后续的训练中使用。DQN中还有两个非常重要的模块--经验回放和目标网络，他们能够帮助DQN取得稳定、出色的性能。

7.3.1 经验回放

在一般的有监督学习中，假设训练数据是独立同分布的，我们每次训练神经网络的时候从训练数据中采样一个或若干个数据来进行梯度下降，随着学习的不断进行，每一个训练数据会被使用多次。在原来的Q-learning算法中，每一个数据只会用来更新一次Q值。为了更好地将Q-learning和深度神经网络结合，DQN算法采用了经验回放方法，具体做法为维护一个回放缓冲区，将每次从环境中采样得到的四元组数据（状态、动作、奖励、下一状态）存储到回放缓冲区中，训练Q网络的时候再从回放缓冲区中随机采样若干数据进行训练。这么做可以起到以下两个作用。

（1）.使样本满足独立假设。在MDP中交互采样得到的数据本身不满足独立假设，因为这一时刻的状态和上一时刻的状态有关。非独立同分布的数据队训练神经网络有很大的影响，会使神经网络拟合到最近训练的数据上。采用经验回放可以打破样本之间的相关性，让其满足独立假设。

（2）提高样本效率。每一个样本可以被使用多次，十分适合深度神经网络的梯度学习。

7.3.2 目标网络

DQN算法最终更新的目标是让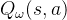 $Q_\omega (s,a)$ 逼近 $r + \gamma max_{a'} Q_\omega (s',a')$ ,由于TD误差目标本身就包含神经网络的输出，因此在更新网络参数的同时目标也在不断地改变，这非常容易造成神经网络训练的不稳定性。为了解决这一问题， DQN便使用了目标网络的思想：既然训练过程中Q网络的不断更新会导致目标不断发生改变，不如暂时先将TD目标中的Q网络固定住。为了实现这一思想，所以需要两套Q网络。

原来的训练网络 $Q_\omega (s,a)$ ,用于计算原先损失函数 $\frac{1}{2} [Q_\omega (s,a) - (r + \gamma max_{a'} Q_{\omega ^ -} (s',a'))]^2$ 中的 $Q_{\omega} (s,a)$ 项，并且使用正常梯度下降方法来进行更新。
目标网络 $Q_{\omega ^ -} (s,a)$ ,用于计算原先损失函数 $\frac{1}{2} [Q_\omega (s,a) - (r + \gamma max_{a'} Q_{\omega ^ -} (s',a'))]^2$ 中的 $(r + \gamma max_{a'} Q_{\omega ^ -} (s',a'))$ 项，其中 $\omega ^ -$ 表示目标网络中的参数。如果两套网络的参数随时保持一致，则仍为原先不够稳定的算法。为了让更新目标更稳定，目标网络并不会每一步都更新。具体而言，目标网络使用训练网络的一台较旧的参数，训练网络 $Q_{\omega} (s,a)$ 在训练中的每一步都会更新，而目标网络的参数每隔C步才会与训练网络同步一次，即 $\omega ^ - \leftarrow \omega$ ,这样做使得目标网络相对于训练网络更加稳定。

综上所述，DQN算法的具体流程如下：

用随机的网络参数 $\omega$ 初始化网络 $Q_\omega (s,a)$
复制相同的的参数 $\omega ^ - \leftarrow \omega$ 来初始化目标网络 $Q_{\omega'}$
初始化经验回放池R
for 序列 $e = 1 \rightarrow E \quad do$
获取环境初始状态
for 时间步 $t = 1 \rightarrow T \quad do$
根据当前网络 $Q_{\omega}(s,a)$ 以 $\epsilon$ -贪婪策略选择动作
执行动作,获得回报,环境状态变为 $s_{t+1}$
将 $(s_t, a_t, r_t, s_{t+1})$ 存储进回放池R中
若R中数据足够，从R中采样N个数据 $\{(s_i, a_i, r_i, s_{i+1})\}_{i=1,...,N}$
对每个数据，用目标网络计算 $y_i = r_i + \gamma max_a Q_{\omega ^ -}(s_{i+1},a)$
最小化目标损失 $L = \frac{1}{N} \sum_i (y_i - Q_{\omega}(s_i, a_i))^2$ ,以此更新当前网络 $Q_{\omega}$
更新目标网络
end for
end for

7.4 DQN代码实践

接下来，我们就正式进入DQN算法的代码实践环节。采用的测试环境是CartPole-v0，其状态空间相对简单，只有4个变量，因此网络结构的设计也相对简单；采用一层128个神经元的全连接并以ReLU作为激活函数。当遇到跟复杂的诸如图像作为输入的环境时，我们可以考虑深度卷积神经网络。

从DQN算法开始，我们会用到rl_utils库，它包含一些函数：绘制移动平均曲线，计算优势函数等。下面面试rl_utils.py的一个实现。

from tqdm import tqdm
import numpy as np
import torch
import collections
import random

class ReplayBuffer:
    def __init__(self, capacity):
        self.buffer = collections.deque(maxlen=capacity) 

    def add(self, state, action, reward, next_state, done): 
        self.buffer.append((state, action, reward, next_state, done)) 

    def sample(self, batch_size): 
        transitions = random.sample(self.buffer, batch_size)
        state, action, reward, next_state, done = zip(*transitions)
        return np.array(state), action, reward, np.array(next_state), done 

    def size(self): 
        return len(self.buffer)

def moving_average(a, window_size):
    cumulative_sum = np.cumsum(np.insert(a, 0, 0)) 
    middle = (cumulative_sum[window_size:] - cumulative_sum[:-window_size]) / window_size
    r = np.arange(1, window_size-1, 2)
    begin = np.cumsum(a[:window_size-1])[::2] / r
    end = (np.cumsum(a[:-window_size:-1])[::2] / r)[::-1]
    return np.concatenate((begin, middle, end))

def train_on_policy_agent(env, agent, num_episodes):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                transition_dict = {'states': [], 'actions': [], 'next_states': [], 'rewards': [], 'dones': []}
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    transition_dict['states'].append(state)
                    transition_dict['actions'].append(action)
                    transition_dict['next_states'].append(next_state)
                    transition_dict['rewards'].append(reward)
                    transition_dict['dones'].append(done)
                    state = next_state
                    episode_return += reward
                return_list.append(episode_return)
                agent.update(transition_dict)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list

def train_off_policy_agent(env, agent, num_episodes, replay_buffer, minimal_size, batch_size):
    return_list = []
    for i in range(10):
        with tqdm(total=int(num_episodes/10), desc='Iteration %d' % i) as pbar:
            for i_episode in range(int(num_episodes/10)):
                episode_return = 0
                state = env.reset()
                done = False
                while not done:
                    action = agent.take_action(state)
                    next_state, reward, done, _ = env.step(action)
                    replay_buffer.add(state, action, reward, next_state, done)
                    state = next_state
                    episode_return += reward
                    if replay_buffer.size() > minimal_size:
                        b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                        transition_dict = {'states': b_s, 'actions': b_a, 'next_states': b_ns, 'rewards': b_r, 'dones': b_d}
                        agent.update(transition_dict)
                return_list.append(episode_return)
                if (i_episode+1) % 10 == 0:
                    pbar.set_postfix({'episode': '%d' % (num_episodes/10 * i + i_episode+1), 'return': '%.3f' % np.mean(return_list[-10:])})
                pbar.update(1)
    return return_list


def compute_advantage(gamma, lmbda, td_delta):
    td_delta = td_delta.detach().numpy()
    advantage_list = []
    advantage = 0.0
    for delta in td_delta[::-1]:
        advantage = gamma * lmbda * advantage + delta
        advantage_list.append(advantage)
    advantage_list.reverse()
    return torch.tensor(advantage_list, dtype=torch.float)

然后定义一个只有一层隐藏层的Q网络

class Qnet(torch.nn.Module):
    ''' 只有一层隐藏层的Q网络 '''
    def __init__(self, state_dim, hidden_dim, action_dim):
        super(Qnet, self).__init__()
        self.fc1 = torch.nn.Linear(state_dim, hidden_dim)
        self.fc2 = torch.nn.Linear(hidden_dim, action_dim)

    def forward(self, x):
        x = F.relu(self.fc1(x))  # 隐藏层使用ReLU激活函数
        return self.fc2(x)

有了这些基本组件之后，接下来开始实现DQN算法

class DQN:
    ''' DQN算法 '''
    def __init__(self, state_dim, hidden_dim, action_dim, learning_rate, gamma,
                 epsilon, target_update, device):
        self.action_dim = action_dim
        self.q_net = Qnet(state_dim, hidden_dim,
                          self.action_dim).to(device)  # Q网络
        # 目标网络
        self.target_q_net = Qnet(state_dim, hidden_dim,
                                 self.action_dim).to(device)
        # 使用Adam优化器
        self.optimizer = torch.optim.Adam(self.q_net.parameters(),
                                          lr=learning_rate)
        self.gamma = gamma  # 折扣因子
        self.epsilon = epsilon  # epsilon-贪婪策略
        self.target_update = target_update  # 目标网络更新频率
        self.count = 0  # 计数器,记录更新次数
        self.device = device

    def take_action(self, state):  # epsilon-贪婪策略采取动作
        if np.random.random() < self.epsilon:
            action = np.random.randint(self.action_dim)
        else:
            state = torch.tensor([state], dtype=torch.float).to(self.device)
            action = self.q_net(state).argmax().item()
        return action

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        q_values = self.q_net(states).gather(1, actions)  # Q值
        # 下个状态的最大Q值
        max_next_q_values = self.target_q_net(next_states).max(1)[0].view(
            -1, 1)
        q_targets = rewards + self.gamma * max_next_q_values * (1 - dones
                                                                )  # TD误差目标
        dqn_loss = torch.mean(F.mse_loss(q_values, q_targets))  # 均方误差损失函数
        self.optimizer.zero_grad()  # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
        dqn_loss.backward()  # 反向传播更新参数
        self.optimizer.step()

        if self.count % self.target_update == 0:
            self.target_q_net.load_state_dict(
                self.q_net.state_dict())  # 更新目标网络
        self.count += 1

接下来是开始进行训练。

lr = 2e-3
num_episodes = 500
hidden_dim = 128
gamma = 0.98
epsilon = 0.01
target_update = 10
buffer_size = 10000
minimal_size = 500
batch_size = 64
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
    "cpu")

env_name = 'CartPole-v0'
env = gym.make(env_name)
random.seed(0)
np.random.seed(0)
env.seed(0)
torch.manual_seed(0)
replay_buffer = ReplayBuffer(buffer_size)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = DQN(state_dim, hidden_dim, action_dim, lr, gamma, epsilon,
            target_update, device)

return_list = []
for i in range(10):
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):
            episode_return = 0
            state = env.reset()
            done = False
            while not done:
                action = agent.take_action(state)
                next_state, reward, done, _ = env.step(action)
                replay_buffer.add(state, action, reward, next_state, done)
                state = next_state
                episode_return += reward
                # 当buffer数据的数量超过一定值后,才进行Q网络训练
                if replay_buffer.size() > minimal_size:
                    b_s, b_a, b_r, b_ns, b_d = replay_buffer.sample(batch_size)
                    transition_dict = {
                        'states': b_s,
                        'actions': b_a,
                        'next_states': b_ns,
                        'rewards': b_r,
                        'dones': b_d
                    }
                    agent.update(transition_dict)
            return_list.append(episode_return)
            if (i_episode + 1) % 10 == 0:
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)

接下来绘制结果：

episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('DQN on {}'.format(env_name))
plt.show()

可以看到，DQN 的性能在 100 个序列后很快得到提升，最终收敛到策略的最优回报值 200。我们也可以看到，在 DQN 的性能得到提升后，它会持续出现一定程度的震荡，这主要是神经网络过拟合到一些局部经验数据后由argmax运算带来的影响。