Bootstrap

数据结构—图

文章目录

定义

图G是由一个非空的顶点集合V和一个描述顶点之间的关系即边集E的一种数据结构，记为G = (V，E)

1、图G不可以为空，E可以为空，但V一定是非空集

2、图分为无向图和有向图

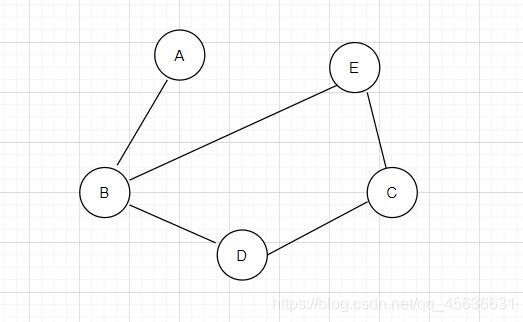
① 无向图：若E为无向边的有限集合，则G为无向图。

边是顶点的无序对，记为 ( v 1 ， v 2 ) (v_1，v_2) (v1​，v2​)或 ( v 2 ， v 1 ) (v_2，v_1) (v2​，v1​)，且 ( v 1 ， v 2 ) = ( v 2 ， v 1 ) (v_1，v_2) = (v_2，v_1) (v1​，v2​)=(v2​，v1​)，v1和v2互为邻接点

G可以表示为：

G = (V，E)​

V = {A，B，C，D，E}

E = {(A，B)，(B，D)，(B，E)，(C，D)，(C，E)}

如图：

无向图

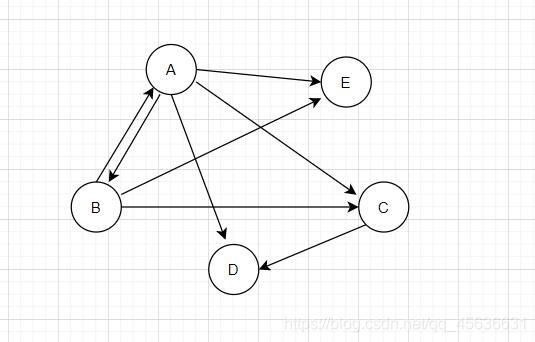
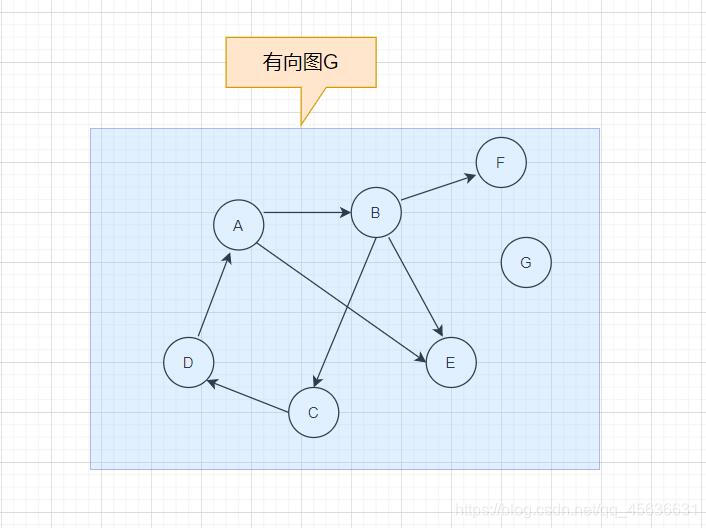
② 有向图：若E为有向边(也称弧)的有限集合，则G为有向图。

弧是顶点的有序对，记为 < v i , v j > <v_i,v_j> <vi​,vj​>，其中 v i v_i vi​是弧尾， v j v_j vj​是弧头

G可以表示为：

G = (V，E)​

V = {A，B，C，D，E}

E = {<A，B>，<A，C>，<A，D>，<A，E>，<B，A>，<B，C>，<B，E>，<C，D>}

如图：

有向图

基本术语

1、顶点的度、入度、出度

① 无向图：顶点的度是指该顶点拥有的边数，记为TD(v)

如上图中：TD(A) = 1，TD(B) = 3，TD© = 2，TD(D) = 2，TD(E) = 2

对于无向图而言，有： ∑ i = 1 n T D ( v i ) = 2 ∣ E ∣ \displaystyle \sum^{n}_{i=1}{TD(v_i)} = 2|E| i=1∑n​TD(vi​)=2∣E∣

② 有向图：入度是以该顶点为终点的有向边的数目，记为ID(v)，出度是以该顶点为起点的有向边的数目，记为OD(v)

顶点v的度等于入度和出度之和，即TD(v) = ID(v) + OD(v)

如上图中：

ID(A) = 1，OD(A) = 4，TD(A) = 5

ID(B) = 1，OD(B) = 3，TD(B) = 4

ID© = 2，OD© = 1，TD© = 3

ID(D) = 2，OD(D) = 0，TD(D) = 2

ID(E) = 2，OD(E) = 0，TD(E) = 2

对于有向图而言，有： ∑ i = 1 n I D ( v i ) = ∑ i = 1 n O D ( v i ) = ∣ E ∣ \displaystyle \sum^{n}_{i=1}{ID(v_i)}=\displaystyle \sum^{n}_{i=1}{OD(v_i)} = |E| i=1∑n​ID(vi​)=i=1∑n​OD(vi​)=∣E∣

2、路径

顶点 v i v_i vi​到 v j v_j vj​之间的一条路径是指顶点序列， v i , v 1 , v 2 , v 3 . . . v j v_i,v_1,v_2,v_3...v_j vi​,v1​,v2​,v3​...vj​

3、回路

第一个顶点和最后一个顶点相同的路径称为回路或环

4、简单路径

在路径序列中，顶点不重复出现的路径称为简单路径

5、简单回路

除第一个顶点和最后一个顶点外，其余顶点不重复出现的回路称为简单回路

6、路径长度

路径上边的数目

7、连通图

无向图中，若从顶点 v i v_i vi​到顶点 v j v_j vj​有路径存在，则称 v i v_i vi​和 v j v_j vj​是连通的，任意两个顶点都是连通的图称为连通图

对于n个顶点的无向图G：

若G为连通图，则最少有n-1条边

若G为非连通图，则最多可能有 C n − 1 2 C_{n-1}^2 Cn−12​条边

8、强连通图

有向图中，若从顶点 v i v_i vi​到顶点 v j v_j vj​和从顶点 v j v_j vj​到顶点 v i v_i vi​都有路径存在，则称 v i v_i vi​和 v j v_j vj​是强连通的，任意两个顶点都是强连通的图称为强连通图

对于n个顶点有向图G：

若G为强连通图，则最少有n条边(形成回路)

9、子图

设有两个图G1 = (V1，E1)和G2 = (V2，E2)，若V2是V1的子集，且E2是E1的子集，则称G2是G1的子图

若G2中包含G1的所有顶点(可以不包含所有的边)，则称G2为G1的生成子图

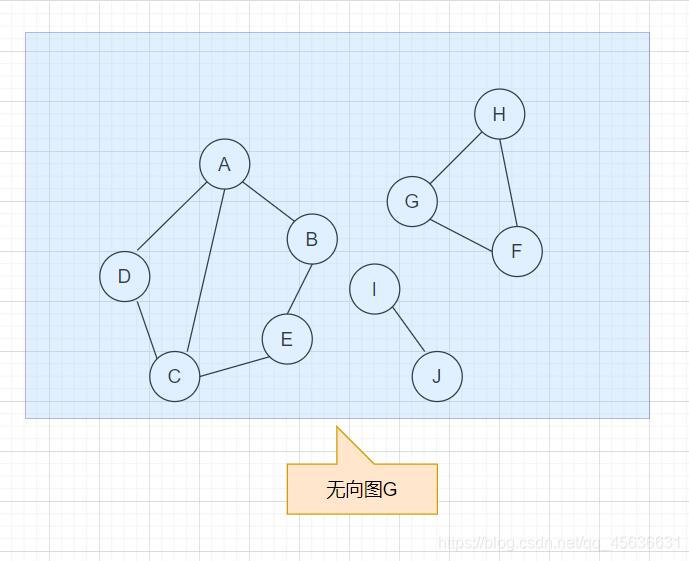
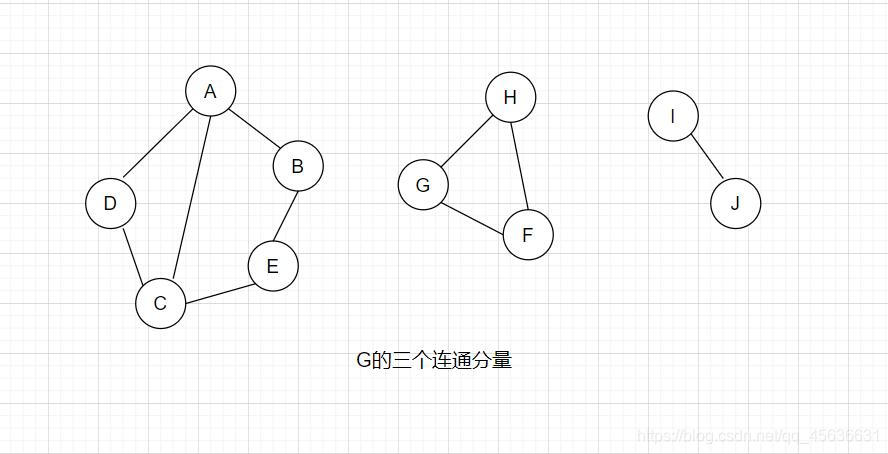
10、连通分量

无向图中的极大连通子图称为连通分量

如图：
连通分量

连通分量

11、强连通分量

有向图中的极大强连通子图称为有向图的强连通分量

如图：

强连通分量

强连通分量

12、生成树

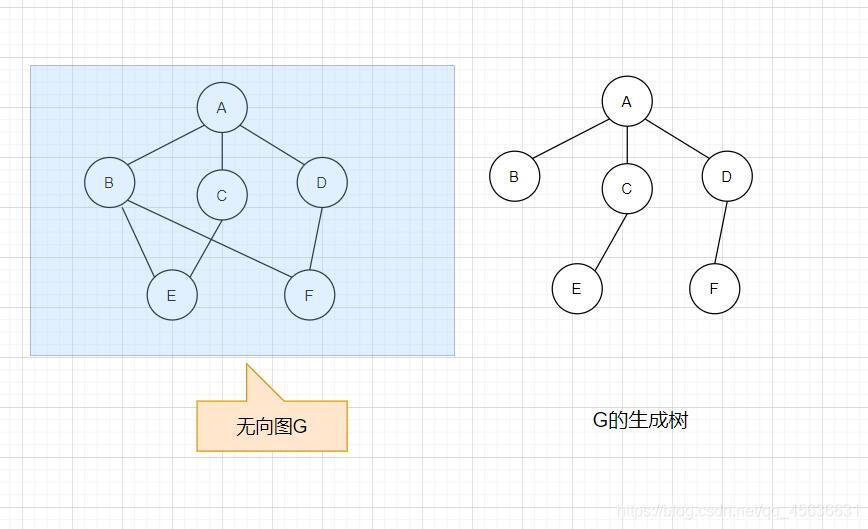
连通图的生成树是包含图中全部顶点的一个极小连通子图

如图：

生成树

生成树是不唯一的

若顶点数为n，则生成树含有n-1条边

对于生成树，去掉一条边，则会变成非连通图，加上一条边则会形成一个回路

13、权

边的权：在一个图中，每条边都可以标上具有某种含义的数值，称为该边的权值

带权图/网：边上带有权值的图称为带权图或者网

带权路径长度：当图是带权图时，一条路径上所有边的权值之和，称为该路径的带权路径长度

14、特殊图

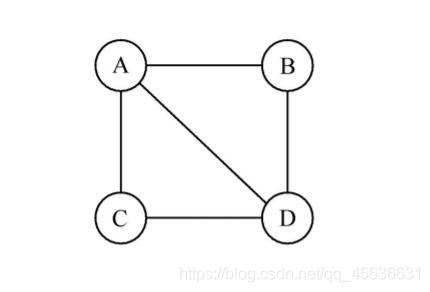
无向完全图：无向图中任意两个顶点之间都存在边

有向完全图：有向图中任意两个顶点之间都存在方向相反的两条弧

若无向图顶点数 ∣ V ∣ = n |V| = n ∣V∣=n，则 ∣ E ∣ ∈ [ 0 , C n 2 ] = [ 0 , n ( n − 1 ) 2 ] |E|\in[0,C^2_n]=[0,\frac{n(n-1)}{2}] ∣E∣∈[0,Cn2​]=[0,2n(n−1)​]

若有向图顶点数 ∣ V ∣ = n |V| = n ∣V∣=n，则 ∣ E ∣ ∈ [ 0 , 2 C n 2 ] = [ 0 , n ( n − 1 ) ] |E|\in[0,2C^2_n]=[0,n(n-1)] ∣E∣∈[0,2Cn2​]=[0,n(n−1)]

图的存储

邻接矩阵法

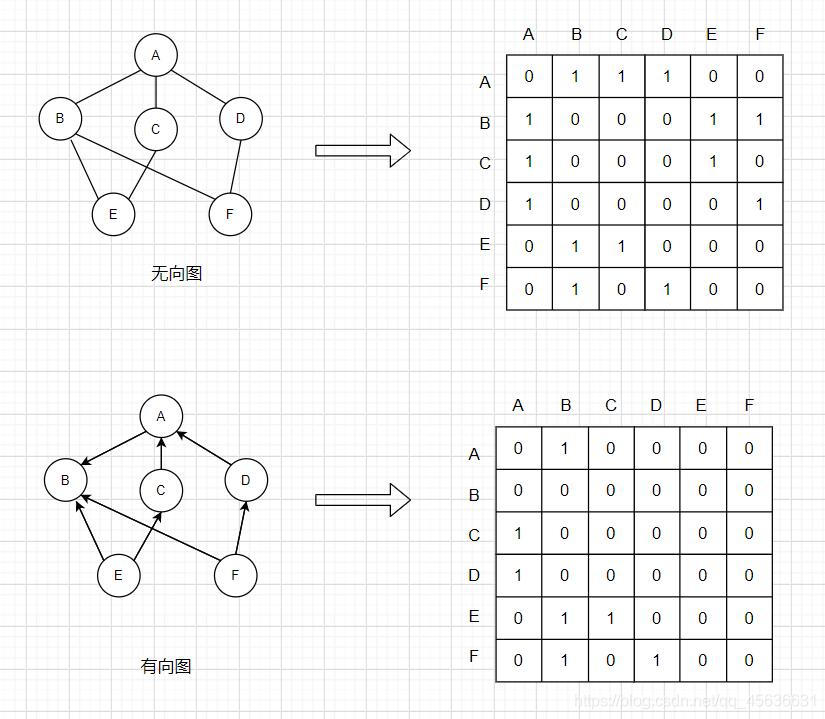
邻接矩阵法是表示顶点之间相邻关系的矩阵

如下图：

邻接矩阵

结构体

#define MaxVertexNum 100
struct Graph {
    char vex[MaxVertexNum];                //顶点表
    int edge[MaxVertexNum][MaxVertexNum];  //邻接矩阵，边表
    int vexNum, edgeNum;                   //顶点数、边数
};

创建图

void CreateGraph(Graph* G) {
    int i, j, k;
    char ch1, ch2;
    cout << "请输入顶点数和边数：";
    cin >> G->vexNum >> G->edgeNum;
    cout << "依次输入各顶点信息：";
    for (i = 0; i < G->vexNum; i++) {
        getchar();
        cin >> G->vex[i];
    }
    for (i = 0; i < G->vexNum; i++) {
        for (j = 0; j < G->vexNum; j++) {
            G->edge[i][j] = 0;
        }
    }
    for (k = 0; k < G->edgeNum; k++) {
        getchar();
        cout << "建立第" << k + 1 << "条边:";
        cin >> ch1 >> ch2;
        for (i = 0; i < G->vexNum; i++) {
            for (j = 0; j < G->vexNum; j++) {
                if (ch1 == G->vex[i] && ch2 == G->vex[j]) {
                    G->edge[i][j] = 1;
                    G->edge[j][i] = 1;
                }
            }
        }
    }
}

打印邻接矩阵

void PrintGraph(Graph *G) {
    int i, j;
    cout << "图的邻接矩阵:" << endl;
    for (i = 0; i < G->vexNum; i++) {
        for (j = 0; j < G->vexNum; j++) {
            cout << G->edge[i][j] << "   ";
        }
        cout << endl;
    }
}

数组实现的顺序存储，空间复杂度高，不适合存储稀疏图

邻接表法

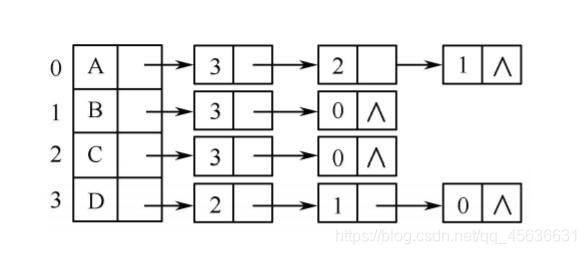
邻接表是图的一种顺序存储与链式存储结合的存储方式，这种方法类似于树的孩子链表表示法。对于图G中的每一个结点，该方法将所有邻接于v的顶点w连成一个单链表，这个单链表就称为顶点v的邻接表，再将所有顶点的邻接表表头放到数组中，就构成了图的邻接表。

如下图：

邻接表

对应的邻接表为：

邻接表

结构体

#define Max 100
int vis[Max];
struct EdgeNode {    //定义边表结点
    int adjVex;      //邻接点域
    EdgeNode* next;  //指向下一个邻接点的指针域
};
struct VexNode {          //定义顶点表结点
    char data;            //顶点域
    EdgeNode* firstEdge;  //指向第一条边结点
};
struct AdjList {
    VexNode adjList[Max];  //邻接表头结点数组
    int vexNum, edgeNum;   //顶点数，边数
};

建立邻接表

void CreateGraph(AdjList* G, int flag) {
    int i, j, k;
    EdgeNode* p;
    if (flag) {
        cout << "建立一个有向图" << endl;
    } else {
        cout << "建立一个无向图" << endl;
    }
    cout << "请输入顶点数和边数：";
    cin >> G->vexNum >> G->edgeNum;
    cout << "依次输入各顶点信息：";
    for (i = 0; i < G->vexNum; i++) {
        // getchar();
        cin >> G->adjList[i].data;
        G->adjList[i].firstEdge = NULL;  //点的边表头指针设为NULL
    }
    cout << "请输入边的信息：" << endl;
    for (k = 0; k < G->edgeNum; k++) {
        cout << "请输入第" << k << "条边：";
        cin >> i >> j;
        p = new EdgeNode;
        p->adjVex = j;  //邻接点序号为i
        p->next = G->adjList[i].firstEdge;
        G->adjList[i].firstEdge = p;
        //将编号为j的结点添加到邻接表中，有向图不用添加
        if (!flag) {
            p = new EdgeNode;
            p->adjVex = i;                      //邻接点序号为i
            p->next = G->adjList[j].firstEdge;  //将新结点p插入到顶点vi边表头
            G->adjList[j].firstEdge = p;
        }
    }
}

打印邻接表

void PrintGraph(AdjList* G) {
    int i;
    EdgeNode* p;
    cout << "图的邻接表表示如下：" << endl;
    for (i = 0; i < G->vexNum; i++) {
        cout << i << " [" << G->adjList[i].data << "]";
        p = G->adjList[i].firstEdge;
        while (p != NULL) {
            cout << "-->[" << p->adjVex << "]";
            p = p->next;
        }
        cout << endl;
    }
}

图的遍历

DFS

图的深度优先搜索(Depth-First-Search)类似于树的先序遍历

方法

1、首先从图中某个顶点发 ｖ 出发，首先访问此顶点，将其标记为已访问过

2、然后任选一个 v 的未被访问的邻接点 ｗ 出发，继续进行深度优先搜索

3、 直到图中所有和 ｖ 路径相通的顶点都被访问到

4、若此时图中还有顶点未被访问到，则另选一个未被访问的顶点作为起始点，重复上面的步骤，直至图中所有的顶点都被访问

代码

//从顶点vex开始遍历
void DFS(AdjList* G, int vex) {
    EdgeNode* p;
    cout << "(" << vex << "," << G->adjList[vex].data << ")";
    vis[vex] = 1;
    p = G->adjList[vex].firstEdge;
    while (p != NULL) {
        if (vis[p->adjVex] == 0) {
            DFS(G, p->adjVex);
        }
        p = p->next;
    }
}

BFS

图的广度优先搜索(Breadth-First-Search)类似于树的层序遍历

方法

1、假设从图中某顶点 ｖ 出发，在访问了 ｖ 之后依次访问 ｖ 的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使 “先被访问的顶点的邻接点” 先于“后被访问的顶点的邻接点” 被访问，直至图中所有已被访问的顶点的邻接点都被访问到

2、若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上 述过程，直至图中所有顶点都被访问到为止3、换句话说，广度优先搜索遍历图的过程中以 ｖ 为起始点，由近至远依次访问和 ｖ 有路径相通且路径长度为 1，2，… 的顶点， 广度优先遍历也需要用到标志数组 vis[N] 以避免重复访问，还需要用到队列来存放已经访问过的各相邻顶点

同一个图的邻接矩阵表示方式唯一，BFS遍历序列唯一

同一个图的邻接表表示方式不唯一，BFS遍历序列不唯一

代码

//从顶点vex开始遍历
void BFS(AdjList* G, int vex) {
    int i, v;
    int q[Max], front = 0, rear = 0; //定义循环队列
    EdgeNode* p;
    for (i = 0; i < G->vexNum; i++) {
        vis[i] = 0;
    }
    cout << "(" << vex << "," << G->adjList[vex].data << ")";
    vis[vex] = 1;
    rear = (rear + 1) % Max;  //队尾指针后移
    q[rear] = vex;  //vex入队
    while (front != rear) {
        front = (front + 1) % Max;
        v = q[front];   //队头出队，赋值给顶点v
        p = G->adjList[v].firstEdge;  //将顶点v的下一条邻接边顶点指针赋值给p
        while (p != NULL) {
            if (vis[p->adjVex] == 0) {  //未访问过
                vis[p->adjVex] = 1;   //访问数组该元素置1，变成已访问
                cout << "(" << p->adjVex << "," << G->adjList[p->adjVex].data << ")";
                rear = (rear + 1) % Max;   //队尾指针后移
                q[rear] = p->adjVex;   //将p所指的顶点入队
            }
            p = p->next;   //p指针后移
        }
    }
}

最小生成树

前面提到了生成树的概念，最小生成树就是连通网G上的一棵各边权值最小的带权生成树，产生一个最小生成树主要有两个算法：普利姆算法和克鲁斯卡尔算法

普利姆算法

思想

从某一个顶点开始构建生成树，每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止

图示

以下两个算法的图片和代码均取自教材

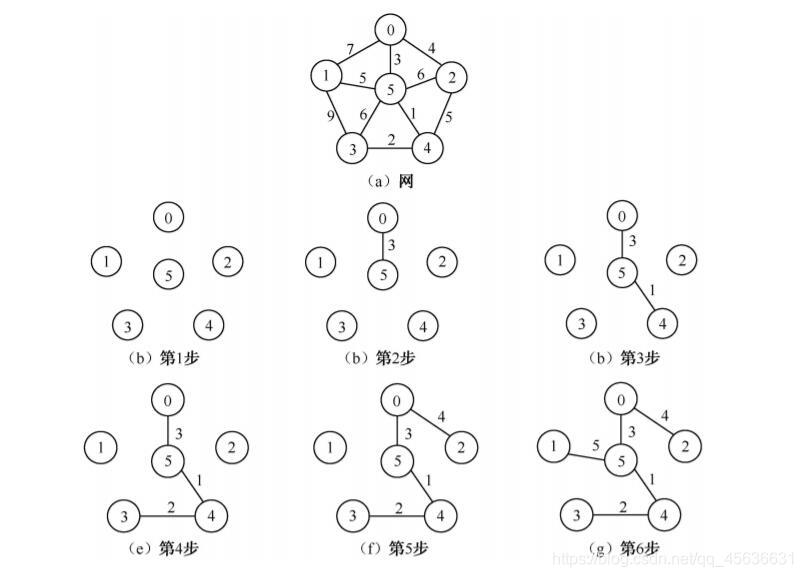
普利姆算法

Prim算法构造最小生成树的过程

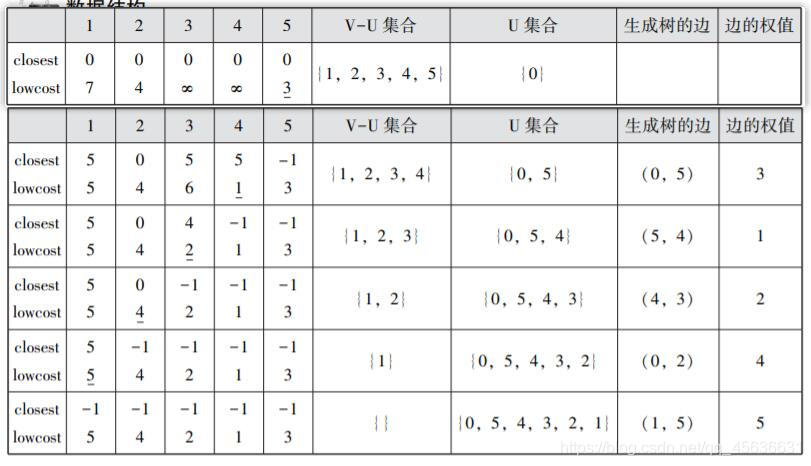
普利姆算法

普利姆算法

用Prim算法构造上图所示连通图的最小生成树过程中各参数的变量示意图

普利姆算法

代码

#include<bits/stdc++.h>

using namespace std;

#define MAX 100
#define M 32767

int CreateCost(int cost[][MAX]) {
    int vexNum, edgeNum, i, j, k, v1, v2, w;
    cout << "请输入顶点数和边数：";
    cin >> vexNum >> edgeNum;
    for (i = 0; i < vexNum; i++) {
        for (j = 0; j < vexNum; j++) {
            cost[i][j] = M;   //预设矩阵中各值为最大值M
        }
    }
    cout << "请输入各边及权值：" << endl;
    for (k = 0; k < edgeNum; k++) {
        cout << "v1 v2 w: ";
        cin >> v1 >> v2 >> w;
        cost[v1][v2] = w;  //将(v1,v2)设权值为w
        cost[v2][v1] = w;  //将(v1,v2)设权值为w
    }
    return vexNum;  //返回顶点数
}

void Prim(int c[MAX][MAX], int n) {
    int i, j, k, min;
    int lowCost[MAX]; //lowCost用来保存集合V-U中各顶点到集合U中各顶点构成的边中具有最小权值的边的权值
    int closest[MAX];   //closest用来保存依附于该边的在集合U中的顶点
    for (i = 1; i < n; i++) {
        lowCost[i] = c[0][i]; //将lowCost数组中各元素设为从顶点0
        closest[i] = 0;  //依附于该边的顶点为0
    }
    closest[0] = -1;  //置初值为-1
    for (i = 1; i < n; i++) {  //从U之外求离U中某一顶点最近的顶点
        min = M;
        k = i;
        for (j = 0; j < n; j++) { //从顶点1开始找各权值中最小值及其依附顶点k
            if (lowCost[j] < min && closest[j] != -1) {
                min = lowCost[j]; //最小值设为当前边的权值
                k = j;   //此边依附顶点赋为j
            } 
        }
        cout << "(" << closest[k] << "," << k << ")" << " 权值 " << lowCost[k] << endl; //打印生成树该边及其权值
        closest[k] = -1;   //k加入到U中
        for (j = 1; j < n; j++) {  //设顶点k为下次查找的起始点
            if (closest[j] != -1 && c[k][j] < lowCost[j]) {
                lowCost[j] = c[k][j];
                closest[j] = k;
            }
        }
    }
}

int main() {
    int n;                 //图中顶点个数
    int cost[MAX][MAX];    //邻接矩阵数组
    n = CreateCost(cost);  //调用建立邻接矩阵函数
    cout << "最小生成树为：" << endl;
    Prim(cost, n);         //调用普利姆算法
}

克鲁斯卡尔算法

思想

每次选择一条权值最小的边，使这条边的两头连通，如果之前已连通的就不选，直到所有点都连通

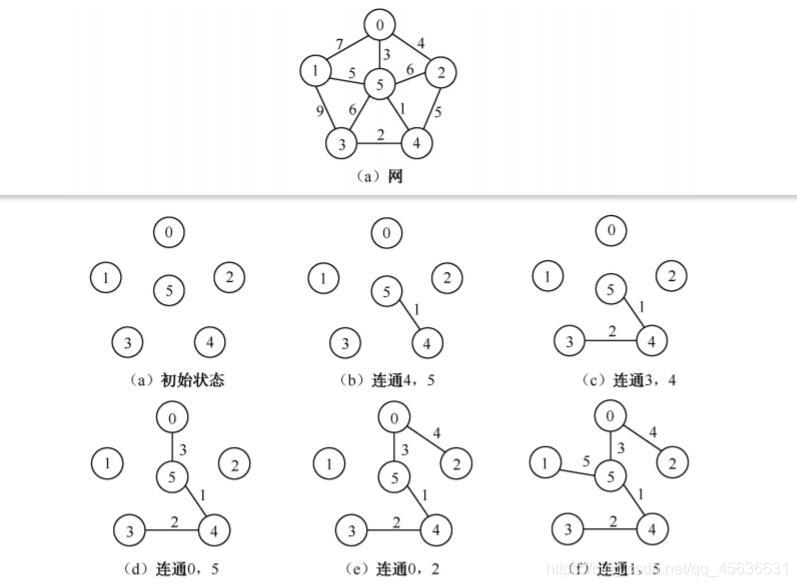
图示

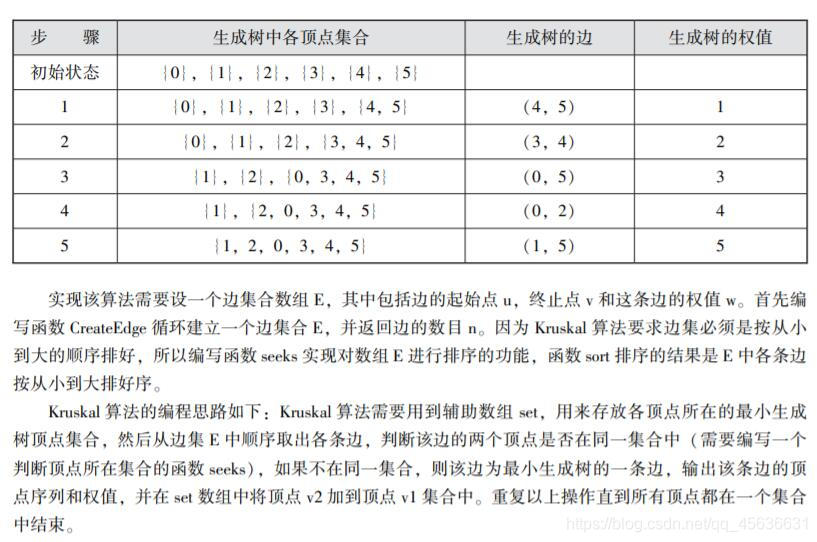
在这里插入图片描述

在这里插入图片描述

用Kruskal算法生成最小生成树时生成树顶点集合的变化过程

在这里插入图片描述

代码

#include<bits/stdc++.h>

using namespace std;

#define MAX 100
struct Edge {
    int u; //边的起始顶点
    int v; //边的终止顶点
    int w; //边的权值
};
Edge E[MAX]; //定义全局数组E，用于存储图的各条边

int CreateEdge() {
    int vexNum, i;
    cout << "请输入无向网的边数：";
    cin >> vexNum;
    for (i = 0; i < vexNum; i++) {
        cout << "v1 v2 w = ";
        cin >> E[i].u >> E[i].v >> E[i].w;
    }
    return vexNum;
}

//为边表进行从小到大排序算法
void sort(int n) {
    int i, j;
    Edge t;
    for (i = 0; i < n - 1; i++) {
        for (j = i + 1; j < n; j++) {
            if (E[i].w > E[j].w) {
                swap(E[i], E[j]);
            }
        }
    }
}

//在边表中查看顶点v在哪个连通集合中
int seek(int set[], int v) {
    int i = v;
    while (set[i] > 0) {
        i = set[i];
    }
    return i;
}

void Kruskal(Edge E[], int n) {
    int set[MAX];   //辅助标志数组
    int v1, v2, i;
    for (i = 0; i < MAX; i++) {
        set[i] = 0;  //set中每个元素赋初值
    }
    i = 0;  //i表示待获取的生成树中的边数，初值为1
    while (i < n) {  //按边权递增顺序，逐边检查该边是否应加入到生成树中
        v1 = seek(set, E[i].u);  //确定顶点v所在的连通集
        v2 = seek(set, E[i].v);
        if (v1 != v2) { //当v1，v2不在同一顶点集合，确定该边应当选入生成树
            cout << "(" << E[i].u << "," << E[i].v << ")" << " 权值 " << E[i].w << endl;
            set[v1] = v2;
        }
        i++;
    }
}

int main() {
    int n;
    n = CreateEdge(); //调用生成边表函数
    sort(n);   //对边表集合进行排序
    cout << "最小生成树为：" << endl;
    Kruskal(E, n);   //调用克鲁斯卡尔算法求最小生成树
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
题目二：设计一个登陆程序，不同的用户名和对应密码存在一个字典里面，输入正确地用户和密码去登陆
matlab中矩阵运算
pyinstaller打包exe运行闪退（已解决）
Spring 源码解读：自定义Bean定义与@Bean注解的实现 原创
AI技术变革：社会冲击与应对策略全面分析
HiXray
JavaMail邮件发送相关案例
大彩串口屏开发——U盘和SD识别问题
CVPR2022论文列表（中英对照）
接口幂等性问题
;