剑指Offer51 数组中的逆序对

我的刷题笔记
数组中的逆序对

1.读题

可以说是归并排序的一道模板题了？

2.解题思路

参考了大佬的题解 暴力解法、分治思想
下面这个题解要好理解很多呐！
剑指 Offer 51. 数组中的逆序对（归并排序，清晰图解）
第一次尝试暴力解法…这也算是个惭愧的点吧QAQ
然后就是参考了下大佬的归并排序的思路~
来看下使用分治思想解题的思路

分治思想（借助归并排序统计逆序数）

要编写一个 “每一次都一分为二拆分数组的子区间” 的递归函数
之后在方法栈弹出的时候 一步一步地合并两个有序数组，最后完成排序工作

• 我们要清楚 利用 归并排序 计算逆序对 是非常经典的做法！！！
• 关键在于：合并两个有序数组 的步骤利用数组的部分有序性（计算逆序数发生在归并排序的过程中！因为我们利用了排序过后数组的有序性）算出一个数之前/之后元素的逆序的个数
• 前面进行归并排序的时候不用统计逆序数的数量 等合并两个有序数组的过程中再进行“逆序对”个数的计算

我们要清楚 逆序对 来源于三个部分

• 左边区间的逆序对
• 右边区间的逆序对吧
• 横跨两个区间的逆序对

3.代码逻辑

merge_sort() 归并排序与逆序对统计：

1. 终止条件： 当 l ≥ r 时，代表子数组长度为 1 ，此时终止划分；
2. 递归划分： 计算数组中点 m ，递归划分左子数组 merge_sort(l, m) 和右子数组 merge_sort(m + 1, r) ；
3. 合并与逆序对统计：

• 暂存数组 nums 闭区间 [i, r] 内的元素至辅助数组 tmp ；
• 循环合并： 设置双指针 i , j 分别指向左 / 右子数组的首元素；
• • 当 i = m + 1 时： 代表左子数组已合并完，因此添加右子数组当前元素 tmp[j] ，并执行 j = j + 1 ；
• • 否则，当 j=r+1 时： 代表右子数组已合并完，因此添加左子数组当前元素 tmp[i] ，并执行 i = i + 1；
• • 否则，当 tmp[i]≤tmp[j] 时： 添加左子数组当前元素 tmp[i]，并执行 i = i + 1；
• • 否则（即 tmp[i] > tmp[j]）时： 添加右子数组当前元素 tmp[j] ，并执行 j = j + 1 ；此时构成 m - i + 1 个「逆序对」，统计添加至 res ；

4. 返回值： 返回直至目前的逆序对总数 res ；

reversePairs() 主函数：

1. 初始化： 辅助数组 tmp ，用于合并阶段暂存元素；
2. 返回值： 执行归并排序 merge_sort() ，并返回逆序对总数即可；

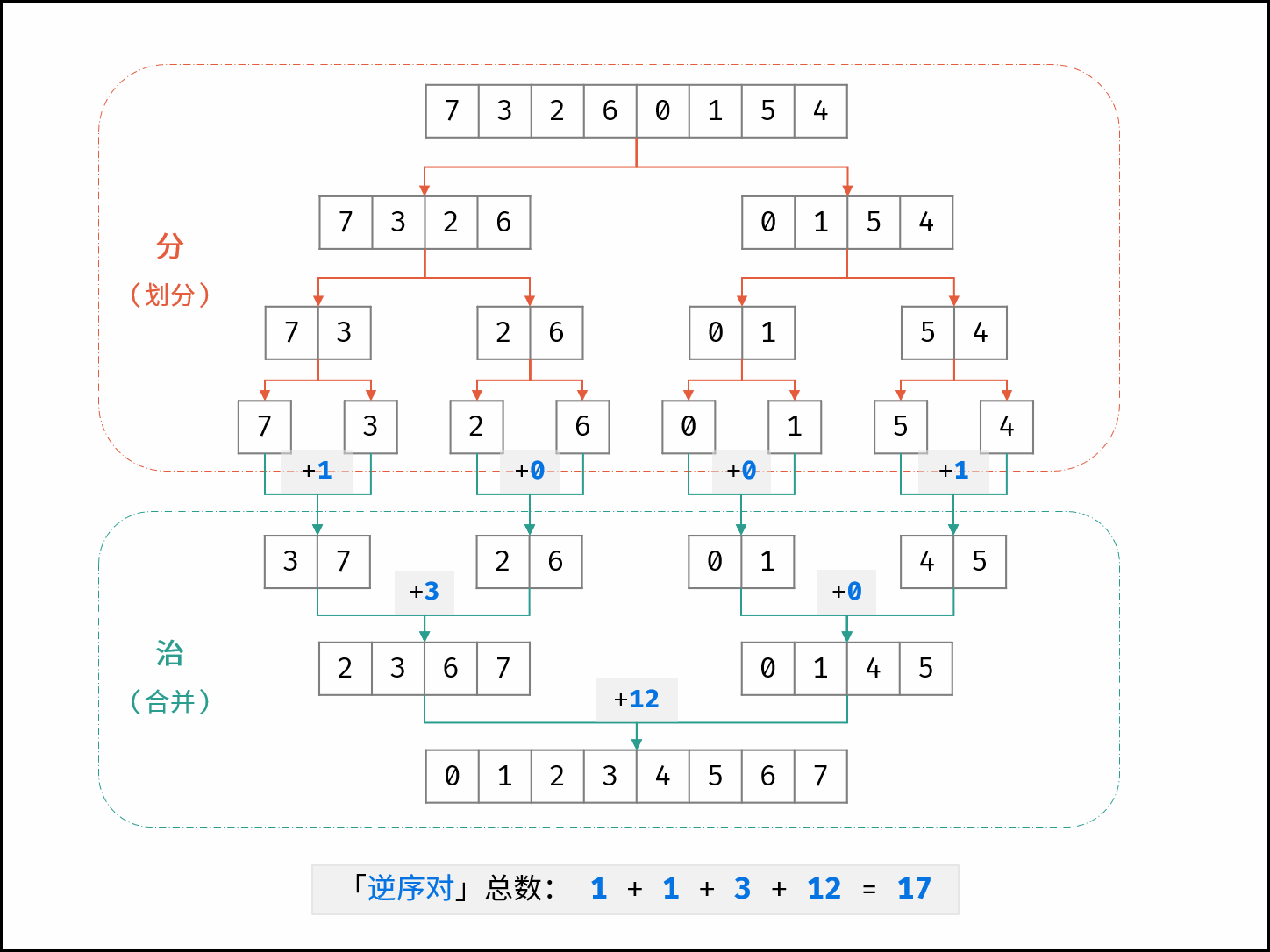
大佬举出一个例子 这样更好理解一些

下图为 数组 [7,3,2,6,0,1,5,4] 的归并排序与逆序对统计过程

有点清晰鸭！

4.Java代码

v1.0 暴力循环解法

public class Solution {
    public int reversePairs(int[] nums){
        int count = 0;
        int len = nums.length;
        for (int i = 0;i < len - 1; i++){
            for (int j = i + 1; j < len; j++){//在除了i之外的数中进行循环查找
                if (nums[i] > nums[j]){
                    count ++;
                }
            }
        }
        return count;
    }
}

成功超时~

v2.0 归并排序 分治思想解题

这个分治思想还是很难理解的哇！！

class Solution {
    int count;
    public int reversePairs(int[] nums) {
        this.count = 0;
        merge(nums, 0, nums.length - 1);
        return count;
    }

    public void merge(int[] nums, int left, int right) {
        int mid = left + ((right - left) >> 1);
        if (left < right) {
            merge(nums, left, mid);
            merge(nums, mid + 1, right);
            mergeSort(nums, left, mid, right);
        }
    }

    public void mergeSort(int[] nums, int left, int mid, int right) {
        int[] temparr = new int[right - left + 1];
        int index = 0;
        int temp1 = left, temp2 = mid + 1;

        while (temp1 <= mid && temp2 <= right) {
            if (nums[temp1] <= nums[temp2]) {
                temparr[index++] = nums[temp1++];
            } else {
                //用来统计逆序对的个数
                count += (mid - temp1 + 1);
                temparr[index++] = nums[temp2++];
            }
        }
        //把左边剩余的数移入数组
        while (temp1 <= mid) {
            temparr[index++] = nums[temp1++];
        }
        //把右边剩余的数移入数组
        while (temp2 <= right) {
            temparr[index++] = nums[temp2++];
        }
        //把新数组中的数覆盖nums数组
        for (int k = 0; k < temparr.length; k++) {
            nums[k + left] = temparr[k];
        }
    }
}

LC92 反转链表II

又见面了老弟！
反转链表II

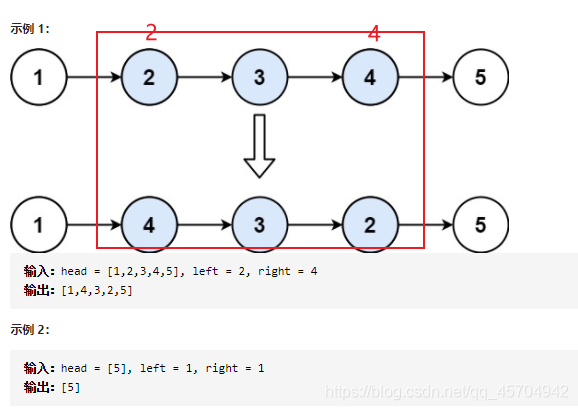
1.读题

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

2.注释齐全的Java代码

class Solution {
    public ListNode reverseBetween(ListNode head, int m, int n) {
        ListNode dummyNode = new ListNode(0);
        //因为头节点可能会发生变化 所以使用虚拟头节点可以避免复杂的分类讨论
        dummyNode.next = head;//虚拟头节点指向头节点

        ListNode g = dummyNode;
        ListNode p = dummyNode.next;//初始化两个指针（LC206中熟悉的操作鸭）

        for (int step = 0; step < m - 1; step++) {
            //第一步 
            //g从虚拟头节点走m-1步 来到m节点的前一个节点————即第一个要反转的节点的前面
            //p从虚拟头节点的下一个位置走m-1步 来到m节点
            g = g.next;
            p = p.next;
        }

        //第二步
        //头插法插入节点
        for (int i = 0; i < n-m; i++){
            //【1】定义删除p后面的节点 为 removed
            ListNode removed = p.next;
            //【2】p指向删除掉元素的下一个节点
            p.next = p.next.next;

            //【3】删除节点指向p节点（也就是g.next)
            removed.next = g.next;
            //【4】最后一步 将g与删除节点连接起来
            g.next = removed;
        }
        
        return dummyNode.next;
    }
}