力扣树专题-4 用leetcode104求树的深度举例总结递归秒杀树问题的套路！ java刷题笔记

听不少大佬建议过——力扣刷题要从树开始！
因为可以建立起套路化的思路~ 另外就是锻炼好递归的思想
所以我们从树开始~
本专题采用前面提到的 “兔系刷题法”
不求钻研多种解法只求快速见题型快速刷题！

另外力扣评论区里看见的——

树的题目写不出来，多背几个模版就行。

前中后序、广度深度遍历、路径和、深度，直径，这些全部背下来。

感觉很有道理！多背些多理解些套路嘛！

本期选取了一道我非常耐的题
来细扣一下递归的这些个小套路~
【图片源自b站迷糊老师】hhh
在这里插入图片描述

不废话先来看题

题目中的“自底向上” "自顶向下”在下面会进行一个详解

2021.6.25 更新 leetcode110 平衡二叉树练一下吧朋友们一模一样的思路

本文食用建议

打开104. 二叉树的最大深度

打开本文
用个30-60min 把这题以及相关方法整明白
啥？时间不够？收藏下慢慢看呗[doge]

另外有什么相关题你做到的时候想到这个小套路了？
评论区见！
（之后我要是遇到可以用这类方法解决的题目会更新进来的~）
在这里插入图片描述

104.二叉树的最大深度

递归

深度优先搜索 DFS

104. 二叉树的最大深度 easy

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

返回它的最大深度 3 。

解题思路

【1】自顶向下

21.6.26更新这里注意自顶向下对于同一个节点，
递归函数会被重复调用，导致时间复杂度较高 为O(N)

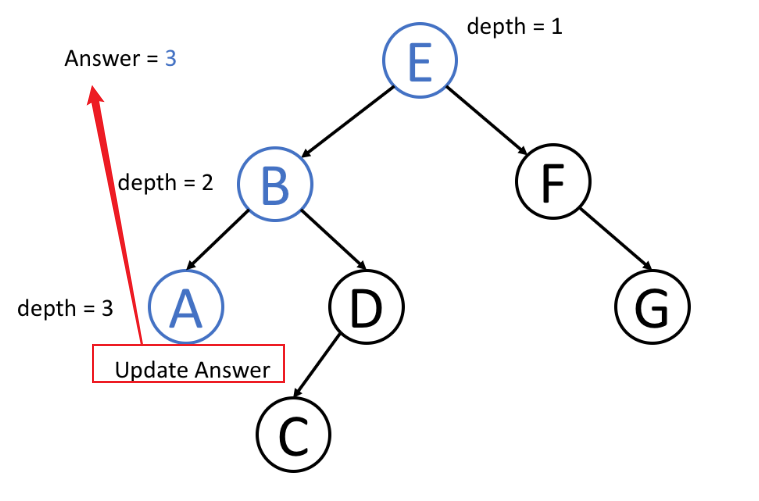
在这里插入图片描述
具体思路就是

一层一层地进行搜索

每搜索新的一层深度 depth 就 +1

到最底下更新一下 ans

【2】自底向上

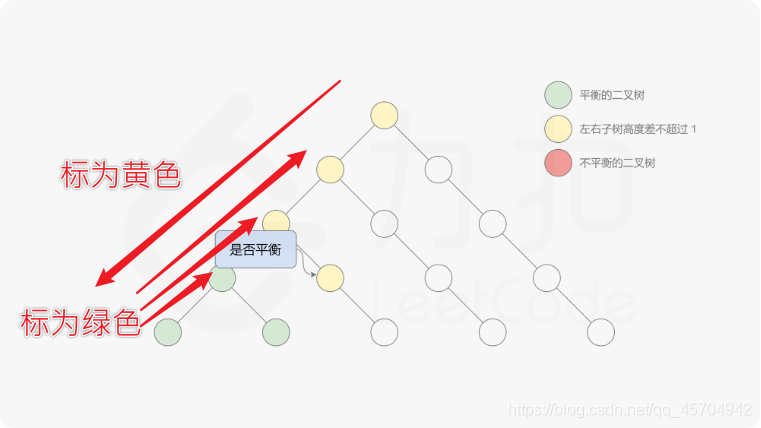
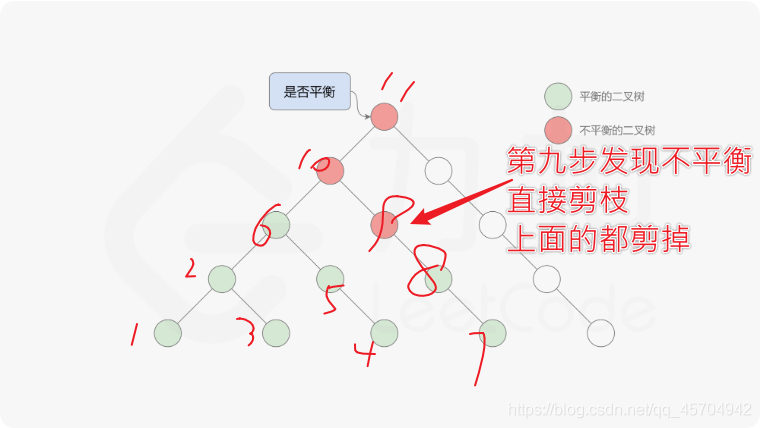
21.6.26更新这里注意自底向上注意这个方法是“提前阻断”的
也就是说一旦碰到了不满足平衡二叉树的节点就会进行“剪枝” （子节点剪掉的话父节点同样剪掉）

在这里插入图片描述
这个方法之前写过一篇博客
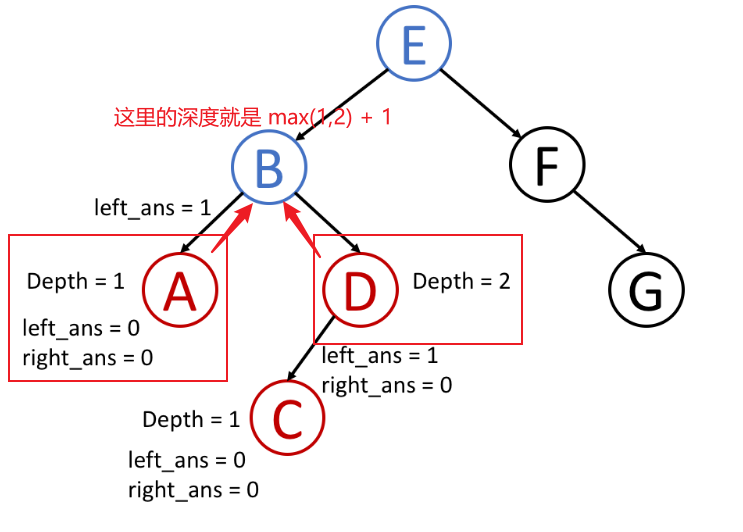
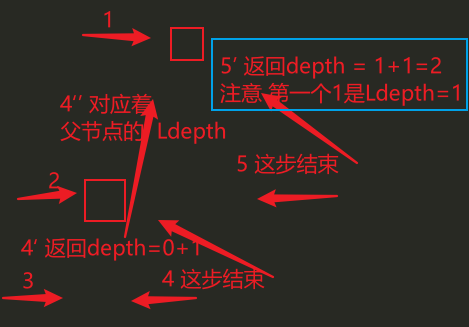
简单画了一下这个寻找depth值的过程刚好吻合~

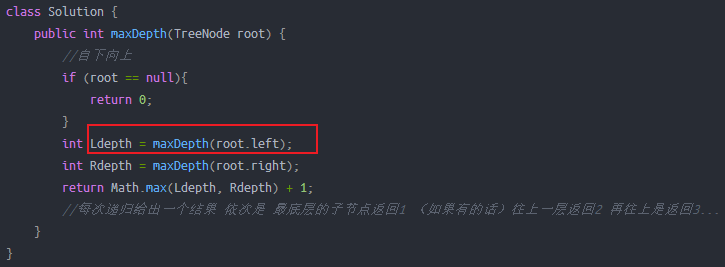
发现叶子节点 ------ return 0 + 1
这个 0 + 1 就是父节点的 Ldepth （看下面的代码）

然后再慢慢往上倒就行了~
如果有上一层 ------ return Math.max(1, Rdepth) + 1
再往上同理

递归自顶向下

关键是计算深度方法 public void _maxDepth(TreeNode root, int depth)

class Solution {
   
    public int ans = 0;
    public void _maxDepth(TreeNode root, int depth) {
   
        if (root == null) return;
        if (root.left == null && root.right == null){
   
            ans = Math.max(ans