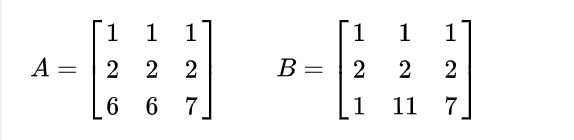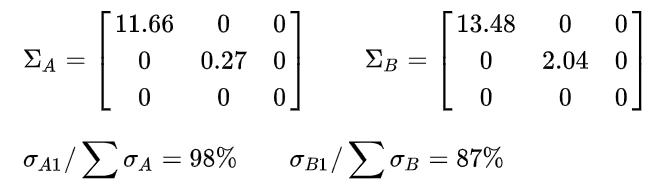本人以光速紧接着上篇CP 和NMF 分解后日夜兼程 完成了这篇张量分解的续集，希望大家多多点赞，这一期我们将学习举足轻重的奇异值分解的相关知识和张量的压缩与Tucker分解，难度依然不小，后期也会为大家附上代码，希望大家能潜心钻研！

一 . 奇异值分解原理

奇异值分解是一个有着很明显的物理意义的一种方法，它可以将一个比较复杂的矩阵用更小更简单的几个子矩阵的相乘来表示，这些小矩阵描述的是矩阵的重要的特性！

特征值分解和奇异值分解两者有着很紧密的关系，特征值分解和奇异值分解的目的都是一样，就是提取出一个矩阵最重要的特征，但奇异值分解是特征分解在任意矩阵上的推广，我们我们还是要先来看看这个特征分解吧~~
$$\mathbf{A}v=\lambda v$$
这里的$v$就是矩阵$\mathbf{A}$ 的特征向量，$\lambda$ 也就是特征值了，这个求出来的特征向量相互之间也都是相互正交的，线代必备警告！

那特征值分解就是将原来的矩阵 $\mathbf{A}$ 分解成如下：
$$A=Q\Sigma Q^{-1}$$
同济线代上其实是有这个知识点的，不知道大家能不能调出尘封已久的记忆，这里的 $Q$ 矩阵是前面特征向量 $v$ 组成的，$\Sigma$ 是由 $\mathbf{A}$ 的特征值组成的对角矩阵 ！

在前面量子计算中我们就曾深入的探讨过各种矩阵，矩阵其实就是一种算子，一种线性变换的工具，如果某个矩阵乘以一个向量得到的新向量，其实就是相当于对原始向量做出了某种变换！在这里，我们依然采用这种方法，通过线性变化去理解它的意义所在：

有个对角矩阵：$M=\left[\begin{array}{ll}3& 0\\ 0& 1\end{array}\right]$ ,乘以平面中的一个向量，如下：

结果为：$\left[\begin{array}{ll}3& 0\\ 0& 1\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]=\left[\begin{array}{l}3x\\ y\end{array}\right]$ ，相当于一个X轴方向上的拉伸，当你改变主对角线上的数字的时候，拉伸或伸缩的效果也是不同，问题又来了，如果不是对角矩阵作用又会是怎样？

当 $M=\left[\begin{array}{ll}1& 1\\ 0& 1\end{array}\right]$ 时，效果如下：

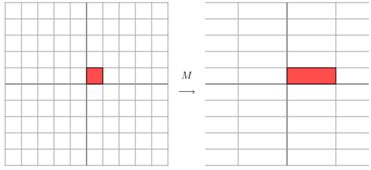
显然这个有点不一样，它其实是将整个平面方格图 沿着蓝色箭头的方向拉伸得到的结果，所以，不同的拉伸方向效果都是来源于不同的矩阵作用，我们只需要通过矩阵直接描述这个变换（拉伸或缩短的）的主要方向就好了！

我们要知道通过特征分解得到的 $\Sigma$ 矩阵中主对角线上特征值的排列顺序是和 $Q$ 矩阵中的特征向量的排列有着一一对应的关系！

当矩阵是高维的情况下，那么这个矩阵就是高维空间下的一个线性变换，这个线性变化可能没法通过图片来表示，但是可以想象，这个变换也同样有很多的变换方向，我们通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。而特征值就像是权重，哪个最大，哪个对应的特征向量方向就占比越大！

总结一下，特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，可以将每一个特征向量理解为一个线性的子空间，我们可以利用这些线性的子空间干很多的事情。不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵(马上就会解决这个问题！)

是不是感觉世界都清晰了，当时理解了这个之后，我TM直接正道的光！我再一次认识到：线性代数是我见过最美妙牛逼的数学，没有之一，不接受反驳，不服来杠 |ू•ૅω•́)ᵎᵎᵎ

简单说了一下特征值分解，我们趁热打铁，直接上奇异值分解的车：

前面说特征值分解虽好，难免有局限性，比如只能是方阵，但是现实应用中强制是方阵明显就是在扯淡，所以，此时奇异值分解就闪亮登场！

$$A=U\Sigma V^T$$
类比思想就很重要！假设 $\mathbf{A}$ 是个$n\times m$ 的矩阵，那么得到的$\mathbf{U}$ 就是一个$n\times n$ 的方阵（其中向量相互正交，且称其为左奇异向量） ， $\mathbf{\Sigma }$ 是一个$n\times m$ 的矩阵（除了对角线的元素都是0，对角线上的元素称为奇异值）, ${\mathbf{V}}^T$ （V矩阵的转置）是一个$n\times n$ 的矩阵，里面的各个向量也是相互正交的！

有小伙伴就问了，上面的介绍的不同向量可以理解，这个奇异值是什么东西，和前面的特征值有啥关系吗，唉，你猜对了，关系大了去了：

$\mathbf{A}{\mathbf{A}}^T$会得到一个方阵，在对这个方阵求特征值可以得到：
$$\left(A^{T}A\right)v_i={\lambda }_i{v}_i$$
这里的 $v_i$ 就是上面刚说的右奇异向量，且：
$$\begin{array}{l}{\sigma }_i=\sqrt{{\lambda }_i}\\ u_i=\frac{1}{{\sigma }_i}A{v}_i\end{array}$$

这里的 ${\mathbf{\sigma }}_{\mathbf{i}}$ 就是上面说的奇异值，${\mathbf{u}}_{\mathbf{i}}$就是上面说的左奇异向量! 这样我们就算是将特征值与奇异值分解联通起来了！

为了让大家更好的理解和使用，在我的纠结下，我还是和大家一块证明一下这个奇异值分解吧！

该部分是从几何层面上去理解二维的SVD：对于任意的 2 x 2 矩阵，通过SVD可以将一个相互垂直的网格图变换到另外一个相互垂直的网格图：

首先选择两个相互正交的单位向量 ${\mathbf{v}}_1$ 和 ${\mathbf{v}}_1$ ，向量 $\mathbf{M}{\mathbf{v}}_1$ 和 $\mathbf{M}{\mathbf{v}}_2$ 正交！

${\mathbf{u}}_1$ 和 ${\mathbf{u}}_2$ 分别是 $\mathbf{M}{\mathbf{v}}_1$ 和 $\mathbf{M}{\mathbf{v}}_2$ 的单位向量（这是另一组正交基）

因为$$\begin{array}{l}M{v}_1={\sigma }_1{u}_1\\ M{v}_2={\sigma }_2{u}_2\end{array}$$

则 ${\sigma }_1,{\sigma }_2$ 分别为$\mathbf{M}{\mathbf{v}}_1$ 和 $\mathbf{M}{\mathbf{v}}_2$ 的模（也称为矩阵$\mathbf{M}$ 的奇异值）。

对于任意向量 $\mathbf{x}$ 有：$\mathbf{x}=\left(v_1\cdot \mathbf{x}\right)v_1+\left(v_2\cdot \mathbf{x}\right)v_2$

别懵，这只是一个数学技巧而已，例如：

当$x=\left[\begin{array}{l}3\\ 2\end{array}\right]$ 时, $x=\left(\left[\begin{array}{l}1\\ 0\end{array}\right]\left[\begin{array}{ll}3& 2\end{array}\right]\right)\left[\begin{array}{l}1\\ 0\end{array}\right]+\left(\left[\begin{array}{l}0\\ 1\end{array}\right]\left[\begin{array}{ll}3& 2\end{array}\right]\right)\left[\begin{array}{l}0\\ 1\end{array}\right]$

整个推导，就这个转化技巧最关键！之后我们运用这个得到：

$$\begin{array}{l}Mx=\left(v_1\cdot x\right)M{v}_1+\left(v_2\cdot x\right)M{v}_2\\ Mx=\left(v_1\cdot x\right){\sigma }_1{u}_1+\left(v_2\cdot x\right){\sigma }_2{u}_2\end{array}$$
因为向量的内积可用向量的转置来表示，所以结合上面的推导：
$$Mx=v_1^{T}x{\sigma }_1{u}_1+v_1^{T}x{\sigma }_2{u}_2$$
同时去掉 $x$:
$$Mx=v_1^T{\sigma }_1{u}_1+v_1^T{\sigma }_2{u}_2$$即：
$$M=U\Sigma V^T$$
证明就算是完成了！

既然大差不差的搞懂了，我们做个题目来实现SVD 的计算：

1. 矩阵$\mathbf{A}$为：$\mathbf{A}=\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$
2. 首先求出 ${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$ 和 $\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$
   $$\begin{array}{l}{\mathbf{A}}^{\mathbf{T}}\mathbf{A}=\left(\begin{array}{lll}0& 1& 1\\ 1& 1& 0\end{array}\right)\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)=\left(\begin{array}{ll}2& 1\\ 1& 2\end{array}\right)\\ \mathbf{A}{\mathbf{A}}^{\mathbf{T}}=\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{lll}0& 1& 1\\ 1& 1& 0\end{array}\right)=\left(\begin{array}{lll}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)\end{array}$$
3. 进而分别求出${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$ 和 $\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$ 的特征值和特征向量：

${\mathbf{A}}^{\mathbf{T}}\mathbf{A}$ ：${\lambda }_1=3;v_1=\left(\begin{array}{c}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right);{\lambda }_2=1;v_2=\left(\begin{array}{c}-1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)$
$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}$ ：${\lambda }_1=3;u_1=\left(\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right);{\lambda }_2=1;u_2=\left(\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right);{\lambda }_3=0;u_3=\left(\begin{array}{c}1/\sqrt{3}\\ -1/\sqrt{3}\\ 1/\sqrt{3}\end{array}\right)$

利用 $A{v}_i={\sigma }_i{u}_i,i=1,2$ 求奇异值：
$$\begin{array}{l}\left(\begin{array}{ll}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{l}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)={\sigma }_1\left(\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right)\Rightarrow {\sigma }_1=\sqrt{3}\\ \left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}-1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)={\sigma }_2\left(\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right)\Rightarrow {\sigma }_2=1\end{array}$$

也可以用 ${\sigma }_i=\sqrt{{\lambda }_i}$ 直接求！

最终得到A的奇异值分解为：
$$A=U\Sigma V^T=\left(\begin{array}{ccc}1/\sqrt{6}& 1/\sqrt{2}& 1/\sqrt{3}\\ 2/\sqrt{6}& 0& -1/\sqrt{3}\\ 1/\sqrt{6}& -1/\sqrt{2}& 1/\sqrt{3}\end{array}\right)\left(\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right)\left(\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2}\end{array}\right)$$

奇异值$\mathbf{\sigma }$跟特征值类似，在 $\mathbf{\Sigma }$ 矩阵中也是从大到小排列，而且$\mathbf{\sigma }$的减少的特别快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了！

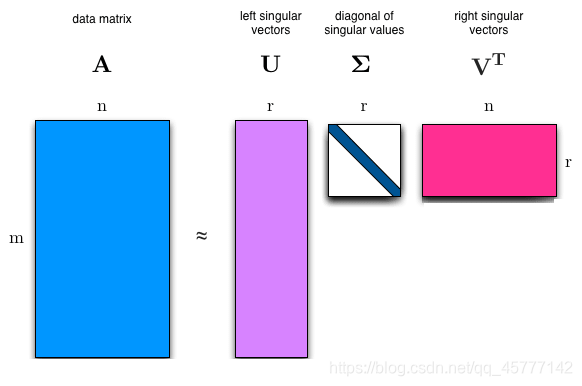
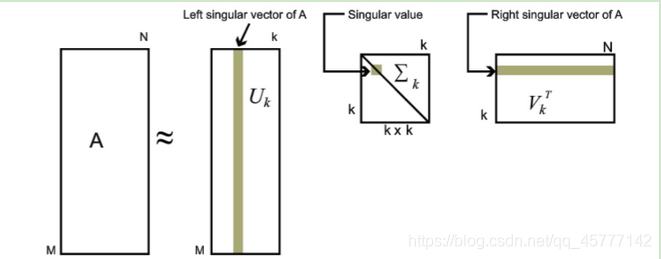
也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵，即：

$$A_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^T\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^T$$
其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵表示即可：

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。

我们上面说推导和证明的奇异值分解方法都是完全奇异值分解，但是实际在图像处理算法中使用的的是奇异值分解的紧凑形式和截断形式。紧奇异值分解是与原始矩阵等秩的奇异值分解，截断奇异值分解是比原始矩阵低秩的奇异值分解，我们简单了解一下就可以了：

1. 紧奇异值分解定义： 对于 $m\times n$ 的实矩阵$\mathbf{A}$ ，秩为：$rank(\mathbf{A})=r⩽min(m,n)$，那么矩阵$\mathbf{A}$ 的 紧奇异值分解 为：
   $$\mathbf{A}={\mathbf{U}}_{\mathbf{r}}{\mathbf{\Sigma }}_{\mathbf{r}}{\mathbf{V}}_{\mathbf{r}}^{\mathbf{T}}$$
   其实就是就是在列的方向上只取前 $r$ 列 即可;
2. 截断奇异值分解定义： 对于 $m\times n$ 的实矩阵$\mathbf{A}$ ，秩 $rank(\mathbf{A})=r$ ,d但是 $0<k<r$,则截断奇异值分解为：
   $$\mathbf{A}\approx {\mathbf{U}}_{\mathbf{k}}{\mathbf{\Sigma }}_{\mathbf{k}}{\mathbf{V}}_{\mathbf{k}}^{\mathbf{T}}$$
   比较二者的公式应该就能明白了，只不过一个是等于号，一个是约等于！

注意：紧奇异值分解还原后等于原矩阵，截断奇异值分解近似还原原矩阵。因此在对矩阵数据进行压缩时，紧奇异值分解对应无损压缩，截断奇异值分解对应有损压缩。

这里为大家附上代码链接：特征值，奇异值分解及其应用

前面的所有所有，都在解释矩阵的奇异值是怎么得到的，包括证明等等，但是奇异值到底是个什么东西，它与矩阵之间有什么千丝万缕的联系么？我们似乎还是有点蒙！

无论是特征值分解还是奇异值分解，都是为了让人们对矩阵（或者线性变换）的作用有一个直观的认识。这是因为我们拿过来一个矩阵，很多情况下只能看到一堆排列有序的数字，而看不到这些数字背后的真实含义，特征值分解和奇异值分解告诉了我们这些数字背后的真实含义，换句话说，它告诉了我们关于矩阵作用的本质信息！

对于奇异值来说，其实他反映的是一个矩阵的“奇异程度”。

这就又让我想到了大一线代课上老师说过：非满秩的方阵就是奇异矩阵，换句话说就是该方阵的行列式为0，但是有没有量化的标准衡量哪个矩阵更不满秩，或者更奇异呢？比如同样两个满秩矩阵，能否看出哪个更“满”，或者两个非满秩且同为秩r的矩阵，哪个更“奇异”呢？

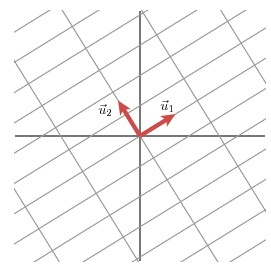
奇异的程度在我看来 秩越低越奇异（目前可以这么理解），相同秩情况下，上图都是秩为2，但我们可以看出A矩阵更接近秩为一！

看看这两个矩阵的奇异值：

猜的没错，第一个矩阵更奇异！

这意味着：一个矩阵越“奇异”，其越少的奇异值蕴含了越多的矩阵信息，矩阵的信息熵越小（这也符合我们的认知，矩阵越“奇异”，其行（或列）向量彼此越线性相关，越能彼此互相解释，矩阵所携带的信息自然也越少）。这些奇异值就是刚才我们所谈论的“本质信息”，而从矩阵中也能得到矩阵的“奇异程度”。

说了那么多，我们最后再来看看奇异值的几个性质：

• 奇异值对矩阵扰动的不敏感性：

  在数学上可以证明，奇异值的变化不会超过相应矩阵的变化，即对任何的相同阶数的实矩阵A、B的按从大到小排列的奇异值${\mathbf{\alpha }}_{\mathbf{i}}$ 和$\mathbf{w}$
  $$\sum \left|{\mathbf{\alpha }}_{\mathbf{i}}-{\mathbf{w}}_i\right|\le \Vert A-B{\Vert }_2$$
  这个性质通常应用于人脸识别中，使用合适的分类器就可以把同一个人的不同姿态，表情的图像矩阵归为一个，具有高容错性！

• 奇异值的比例不变性：

  $\alpha \mathbf{A}$ 的奇异值是 $\mathbf{A}$ 奇异值的 $\left|\alpha \right|$ 倍！

  矩阵进行数乘变换，奇异值也成比例变化。同一个人脸在光线明暗不同情况的图像识别中，它们的矩阵奇异值是成比例变化的。奇异值向量归一化后可以视为一类！

• 奇异值的旋转不变性：

  即若$\mathbf{P}$是正交阵，$\mathbf{P}\mathbf{A}$的奇异值与$\mathbf{A}$的奇异值相同!

  奇异值的比例和旋转不变性特征在数字图象的旋转、镜像、平移、放大、缩小等几何变化方面有很好的应用.

好这一期博客学习就到这里，下期再见！