很高兴在断更这么多天之后,又回到了我最爱的科研学习上面,前段时间我们经历过张量与量子的相爱相杀之后,再回首,看看曾经的量子世界,如果有从头到尾看过本人博客的小伙伴们会发现,自始至终,我们都没有深入学习过量子世界中的概率,作为量子力学的重要组成部分,我们本期博客的主要任务就是学习 “概率”,当然,此“概率”非彼 概率!借此我们来真正的了解之前的 bloch球 问题的 详细内涵!
概率幅与逻辑门
一 . 从概率到概率幅
硬币问题永远都是概率问题的天然例子,假如我们随机抛一枚硬币,显然,我们只能得到是正面朝上或者是反面朝上,都是二分之一的概率,但这是弱智都知道的问题,假如有个未知的模型,对于它可能出现的结果我们并不知道,也就是我们无法直接去观测其事件发生的概率,唯一的办法就是我们做无数次大量重复且独立在相同环境下的实验,最终才能大致的得到每个事件对应的概率!
话又说回来了,现实中哪有那么多次给你重复实验的机会,很多时候都是只有一次机会,所以,这个时候我们就把它称为不可观测的量,这就给我机会用 复数 来重新定义 “概念”这个东西!我们把不可观测的时间用 概率幅 来表示,即:
ψ = a + b i \psi=a+b i ψ=a+bi
因为概率幅的适用范围必然包含“概率”,毫无疑问,可以用概率幅来表示经典概率:
p
=
∣
ψ
∣
2
=
ψ
∗
ψ
=
(
a
−
b
i
)
(
a
+
b
i
)
=
a
2
+
b
2
p=|\psi|^{2}=\psi^{*} \psi=(a-b i)(a+b i)=a^{2}+b^{2}
p=∣ψ∣2=ψ∗ψ=(a−bi)(a+bi)=a2+b2
所以,抛硬币问题我们可以得到正面朝上的概率为: p ( 1 ) = ∣ ψ ( 1 ) ∣ 2 = ( 1 2 ) 2 + ( 1 2 ) 2 = 1 2 p(1)=|\psi(1)|^{2}=\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}=\frac{1}{2} p(1)=∣ψ(1)∣2=(21)2+(21)2=21
因此,我们可以假设在概率背后还有一个更基本的复数概率制约着概率本身。正是因为概率本身并不是一个可以被直接观测到的量,所以我们再做一层复数概率的假设就不会引起实质的困难。尽管我们增加了理论的复杂性,但是我们终于可以成功地将概率复数化了,有了前面的量子基础,再结合这个,是不是突然有许多新的理解和感悟呢??
除此之外,从复数的概率幅到经典的概率是一个多对一的映射,即可能存在多种复数形式却对应同一个概率!我们这里可以用二个式子来表达二者的关系:
P
(
X
)
=
∣
ψ
(
X
)
∣
2
P(X)=|\psi(X)|^{2}
P(X)=∣ψ(X)∣2
ψ
(
X
)
=
P
(
X
)
(
cos
θ
+
i
sin
θ
)
=
P
(
X
)
exp
(
i
θ
)
\psi(X)=\sqrt{P(X)}(\operatorname{cos} \theta+i \sin \theta)=\sqrt{P(X)} \exp (i \theta)
ψ(X)=P(X)(cosθ+isinθ)=P(X)exp(iθ)
显然,下面的式子相当于上面公式的一个反函数,是一个包含复数的反函数,奇妙!!
其中θ 为任意实数。这群复数落到了以原点为圆心,以 P ( X ) \sqrt{P(X)} P(X)为半径的圆上!
这使我又想起来了我们在计算一个单自旋量子叠加态坍缩到本征态的概率并不是单纯的对应本征态前面的系数,而是平方,说明那也是个概率幅,这就通了,亲爱的伙伴们,有没有一种舒畅的感觉!
除了上面说的,这是不是和我们欧拉公式很像啊(链接了虚数世界和实数世界),是不是和我们之前说的bloch球里面的公式也很像呢?别急,我们已经快要找到真相了!
那么对于有多个可能事件的模型来说,我们可以写成向量的形式:
F
(
X
)
=
p
1
∣
x
1
⟩
+
p
2
∣
x
2
⟩
+
⋯
+
p
n
∣
x
m
⟩
F(X)=p_{1}\left|x_{1}\right\rangle+p_{2}\left|x_{2}\right\rangle+\cdots+p_{n}\left|x_{m}\right\rangle
F(X)=p1∣x1⟩+p2∣x2⟩+⋯+pn∣xm⟩
并且满足归一化条件:
∑
i
=
1
n
p
(
x
i
)
=
1
\sum_{i=1}^{n} p\left(x_{i}\right)=1
∑i=1np(xi)=1,这个我们在前面的量子学习和量子计算中出现很多次了,就不再赘述了!
到这里,经典概率和复数组成的概率幅除了在公式和应用范围上的一些不同之外,二者还有最本质的区别:
- 不兼容属性(incompatible property)是量子概率——将概率论扩充到复数域的最特别的概念,也是区别复数概率和经典概率的本质所在。
什么是不兼容? 就像老鼠和猫咪,学生和老师,不能同时存在,或者说有一种类似于互斥的关心!那么我们是否在量子的学习中遇到过类似的不兼容关系??
其实就是量子中的不确定性原理,我们无法在同一时刻知道某个粒子的动量和能量!这样我们就算是从表面上揭示了它的本质,这里老师还为我们提供了一个非常好的例子,是我有史以来见过的最好的描述不确定性的例子:
一个模型有两个属性
A
A
A 和
B
B
B ,其中
A
A
A 的取值有
U
,
D
{U,D}
U,D 两种可能,
B
B
B 的取值有
L
,
R
{L,R}
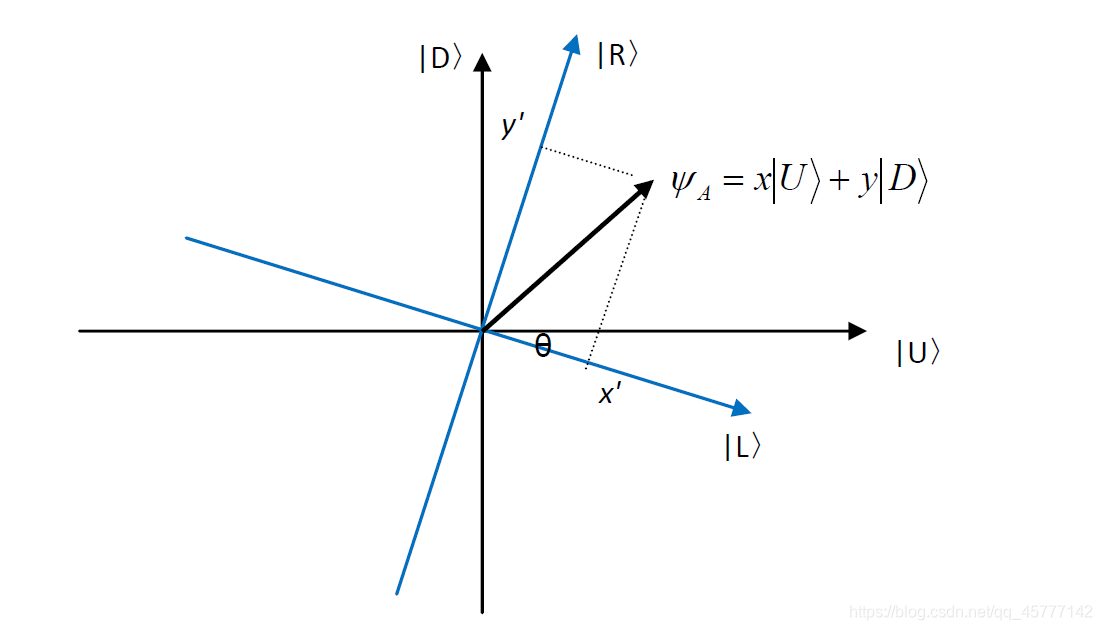
L,R 两种可能,我们在将每个事件中情况的可以用线性空间中相互垂直的的向量来表示,且可以组成两张平面,我们先假设这两张平面重合了,如下图:
前两个事件构成的基向量组成的平面是由黑色坐标轴组成的,后面两个事件组成的平面是由蓝色坐标轴组成的!且这两个平面重合成一个平面,并且二者之间有一个 夹角为
θ
\theta
θ ,那么,在第一个黑色坐标系下,图中的加粗箭头表示的向量是:
ψ
A
=
x
∣
U
⟩
+
y
∣
D
⟩
\psi_{A}=x|U\rangle+y|D\rangle
ψA=x∣U⟩+y∣D⟩,那么接下来,我们如何将它转化到第二个坐标系中呢?下面这个公式就可以:
(
x
′
y
′
)
=
(
cos
θ
sin
θ
−
sin
θ
cos
θ
)
⋅
(
x
y
)
=
(
x
cos
θ
+
y
sin
θ
−
x
sin
θ
+
y
cos
θ
)
\left(\begin{array}{l} x^{\prime} \\ y^{\prime} \end{array}\right)=\left(\begin{array}{cc} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right) \cdot\left(\begin{array}{l} x \\ y \end{array}\right)=\left(\begin{array}{c} x \cos \theta+y \sin \theta \\ -x \sin \theta+y \cos \theta \end{array}\right)
(x′y′)=(cosθ−sinθsinθcosθ)⋅(xy)=(xcosθ+ysinθ−xsinθ+ycosθ)
即:
ψ
B
=
x
′
∣
L
⟩
+
y
′
∣
R
⟩
\psi_{B}=x^{\prime}|L\rangle+y^{\prime}|R\rangle
ψB=x′∣L⟩+y′∣R⟩
之前在学习表象中的坐标表象的时候,曾经简单的介绍过旋转矩阵这个东西,这个再次派上用场了,那么这又和我们的不确定性有啥关系呢??
显然,我们从上面几个式子中可以明确的知道发生 A A A且取值为 U U U 的 概率为: ∣ x ∣ 2 \left | x \right |^{2} ∣x∣2 , 取值为 B B B 的概率为 ∣ y ∣ 2 \left | y \right |^{2} ∣y∣2 ,对于 B B B 事件来说也是同理的,但是由于蓝色式子的限制,所以二者之间必然会存在相互影响, A A A 属性的概率分布肯定会对 B B B 进行干扰,这就是不确定性原理的一个影子!
现在我们再来看一下之前没搞懂的布洛赫球 :
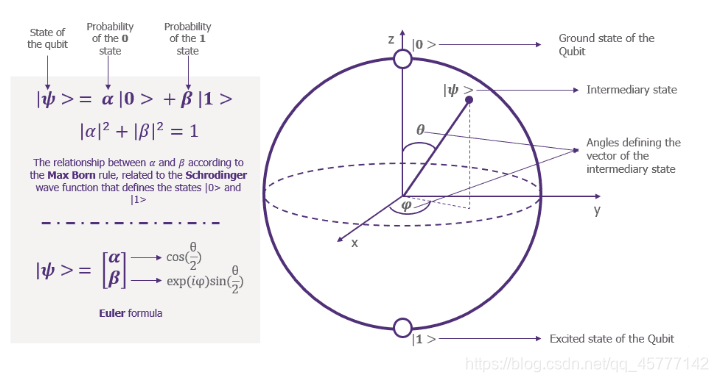
∣
φ
⟩
=
e
i
γ
(
cos
θ
2
∣
0
⟩
+
e
i
ϕ
sin
θ
2
∣
1
⟩
)
|\varphi\rangle=e^{i \gamma}\left(\cos \frac{\theta}{2}|0\rangle+e^{i \phi} \sin \frac{\theta}{2}|1\rangle\right)
∣φ⟩=eiγ(cos2θ∣0⟩+eiϕsin2θ∣1⟩)
其中的
e
i
γ
e^{i \gamma}
eiγ 是个不具有观测意义的整体相位,所以我们可以不用管它,进而得到:
∣
φ
⟩
=
cos
θ
2
∣
0
⟩
+
e
i
ϕ
sin
θ
2
∣
1
⟩
=
[
cos
θ
2
e
i
ϕ
sin
θ
2
]
|\varphi\rangle=\cos \frac{\theta}{2}|0\rangle+e^{i \phi} \sin \frac{\theta}{2}|1\rangle=\left[\begin{array}{c} \cos \frac{\theta}{2} \\ e^{i \phi} \sin \frac{\theta}{2} \end{array}\right]
∣φ⟩=cos2θ∣0⟩+eiϕsin2θ∣1⟩=[cos2θeiϕsin2θ]
为啥会做这样的变换,在这之前我特别迷惑 突然 稀里糊涂的就突然变成这样了,了解本次博客学习之后,你一定会知道这里原先的
α
\alpha
α 和
β
\beta
β 代表的都是复数形式的概率幅,所以这里用欧拉公式把他们具象成具有复数形式的表达式,我们有下面较为详细的数学公式步骤推导:
∣
ψ
⟩
=
a
∣
0
⟩
+
b
∣
1
⟩
=
cos
(
θ
2
)
∣
0
⟩
+
e
i
ϕ
sin
(
θ
2
)
∣
1
⟩
=
cos
(
θ
2
)
∣
0
⟩
+
(
cos
(
ϕ
)
+
i
sin
(
ϕ
)
)
sin
(
θ
2
)
∣
1
⟩
\begin{aligned} |\psi\rangle &=a|0\rangle+b|1\rangle \\ &=\cos \left(\frac{\theta}{2}\right)|0\rangle+e^{i \phi} \sin \left(\frac{\theta}{2}\right)|1\rangle \\ &=\cos \left(\frac{\theta}{2}\right)|0\rangle+(\cos (\phi)+i \sin (\phi)) \sin \left(\frac{\theta}{2}\right)|1\rangle \end{aligned}
∣ψ⟩=a∣0⟩+b∣1⟩=cos(2θ)∣0⟩+eiϕsin(2θ)∣1⟩=cos(2θ)∣0⟩+(cos(ϕ)+isin(ϕ))sin(2θ)∣1⟩
再回头结合图片看看,也许会有不一样的发现!
二 . 量子逻辑门
我们学过电路或者计算机的都知道,经典计算机的线路由连线和逻辑门组成,连线负责传递信息,而逻辑门用来处理信息,所以,逻辑门对于计算机来说是至关重要的,在量子计算机中,又是啥样的呢,看一下在量子计算机中的量子逻辑门:
(1)单量子比特门
既然量子逻辑门是个处理信息的东西,那么我们在已有量子计算的基础上,可以大胆猜测量子逻辑门的本质是我们前面学习了无数次的算符,也就是各种各样的矩阵!
首先可以定义一个量子非门(NOT gate):使得
∣
0
⟩
|0\rangle
∣0⟩和
∣
1
⟩
|1\rangle
∣1⟩ 交换,基于其本身的线性性质,我们可以非常方便的用一个矩阵来表示,如下:
X
≡
[
0
1
1
0
]
X \equiv\left[\begin{array}{ll} 0 & 1 \\ 1 & 0 \end{array}\right]
X≡[0110]
可以对一个简单的叠加态使用一些,看看效果:
X
[
α
β
]
=
[
β
α
]
X\left[\begin{array}{l} \alpha \\ \beta \end{array}\right]=\left[\begin{array}{l} \beta \\ \alpha \end{array}\right]
X[αβ]=[βα]
注意:非门的作用是把 ∣ 0 ⟩ |0\rangle ∣0⟩ 态变成矩阵 X X X 第一列对应的状态,把 ∣ 1 ⟩ |1\rangle ∣1⟩ 变成矩阵 X X X 第二列所对应的状态!
除此之外,对于单一量子门而言,需要满足 酉性(unitary) ,即表示单量子比特门的矩阵 U U U 要满足 U † U = I U^{\dagger} U=I U†U=I,也就是矩阵 U U U 与它的共轭转置乘积为单位阵,这也是对单量子门的唯一要求了,并且一般情况下,都是 2 × 2 2\times2 2×2 的矩阵!
除此之外,还有几个比较常用的单量子门,比如说
Z
Z
Z门 :
Z
≡
[
1
0
0
−
1
]
Z \equiv\left[\begin{array}{rr} 1 & 0 \\ 0 & -1 \end{array}\right]
Z≡[100−1]
它的作用是保持
∣
0
⟩
|0\rangle
∣0⟩不变 ,而是将
∣
1
⟩
|1\rangle
∣1⟩变成 -
∣
1
⟩
|1\rangle
∣1⟩,还有一个最重要的就是
H
a
d
a
m
a
r
d
Hadamard
Hadamard 门:
H
≡
1
2
[
1
1
1
−
1
]
H \equiv \frac{1}{\sqrt{2}}\left[\begin{array}{rr} 1 & 1 \\ 1 & -1 \end{array}\right]
H≡21[111−1]
H
a
d
a
m
a
r
d
Hadamard
Hadamard 门的神奇之处就在于它可以将原本的
∣
0
⟩
|0\rangle
∣0⟩态变到
∣
0
⟩
|0\rangle
∣0⟩和
∣
1
⟩
|1\rangle
∣1⟩的中间叠加态上:
(
∣
0
⟩
+
∣
1
⟩
)
/
2
(|0\rangle+|1\rangle) / \sqrt{2}
(∣0⟩+∣1⟩)/2 ,自然也能把
∣
1
⟩
|1\rangle
∣1⟩态变成
(
∣
0
⟩
−
∣
1
⟩
)
/
2
(|0\rangle-|1\rangle) / \sqrt{2}
(∣0⟩−∣1⟩)/2
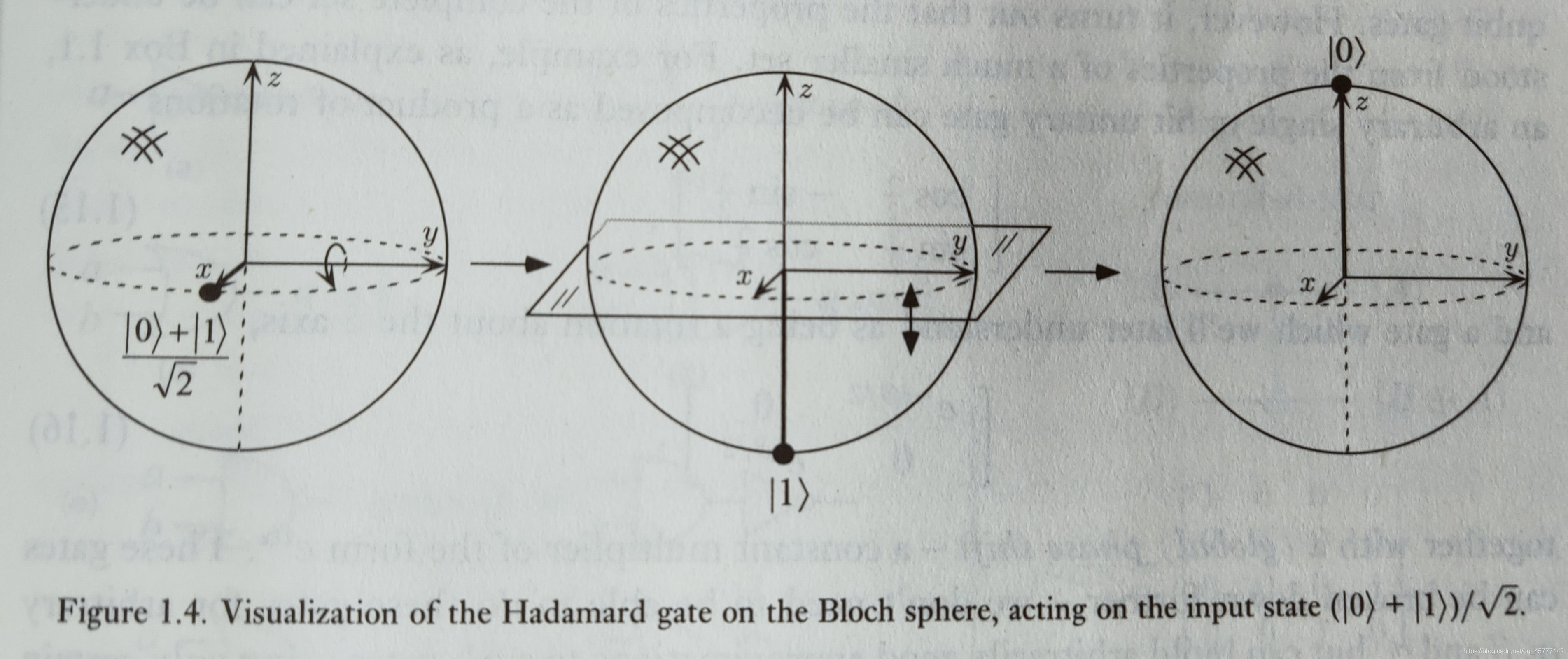
大家也可以在bloch球中看一下 这个 H a d a m a r d Hadamard Hadamard 门是怎么工作的:
可以看出它是先绕
y
y
y 轴旋转 90度,再绕
x
x
x 轴 旋转180度!
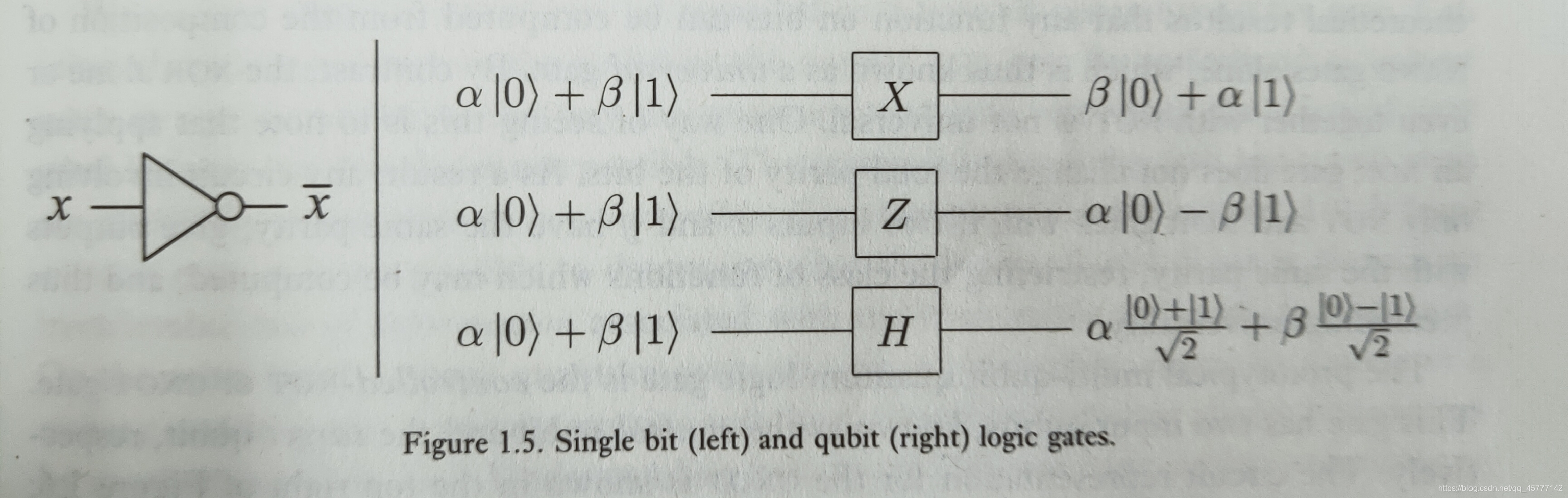
我们用来总结一下常见三个量子比特门作用和效果:
下期博客我们介绍多量子门的相关内容,さようなら!