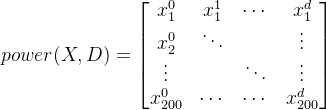目录
一、模型选择
1.泛化误差
机器学习的目标是通过对先存数据的分析发现事件的内在规律,即为模式(Pattern)。因而评价一个机器学习模型优异的标准就是它是否具有良好的泛化能力,这要求所训练的模型不仅是在训练集的数据上有不错的拟合效果,还要在从未见过的新的数据上有可观的表现。只有达到这个目标,机器学习才有它的实用价值,才能凸显其智能性。
于是为了评价一个模型泛化能力,我们引入泛化误差的概念。泛化误差是指模型应用在与原始样本同分布的无限多数据中进行抽取,测试,所得模型误差的期望,相当于模型在海量的新数据中预测效果的平均水平。实际中,数据的获取并非易事,我们通常将模型应用于一个独立的测试集来估计它的泛化误差。
2.举个例子:坏死细胞识别
例如,如果我们想要识别一个小鼠上皮细胞是否已经坏死,而我们发现坏死细胞和存活细胞的表面形貌有明显的差异,那么我们可以认为细胞的存活状态与它的表面形貌有比较强的相关关系。于是我们可以收集一些小鼠上皮细胞的显微拍摄照片作为数据。
照片中的小鼠上皮细胞既有坏死的,也有存活的。接下来我们需要找到一些可以描述细胞表面形貌的特征参数,比如表面积,表面粗糙度等。这些特征最好是可以直接在照片中观察到,以便我们通过像素点的属性值来对特征进行量化。
我们再将每张图像的特征值与它所对应的标签(存活或是坏死)对应起来,就得到了我们需要的数据集。我们把总的数据分成俩部分,第一部分用来训练模型,第二部分用来测试模型。我们还要选择一种机器学习方法,比如MLP等,预设好某些参数。在训练集上训练完成后,需要在训练数据之外的其他新的细胞图像上进行测试,输出细胞的类别(存活状态)。我们可以进行大量这样的测试,将测试的结果与细胞的真实状态进行比较,得到一个平均的准确水平,即为该模型的泛能力。
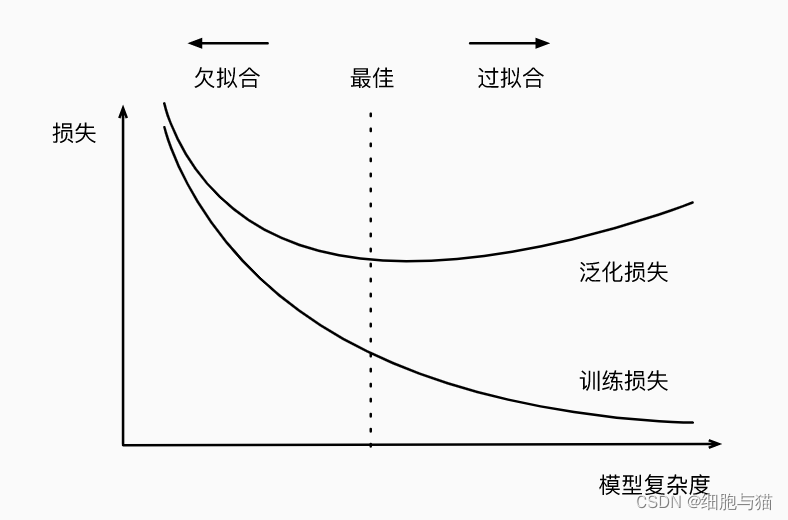
3.过拟合与欠拟合
通常,如果一个模型在训练集上的拟合度较高,往往在测试集上的拟合效果并不理想,这种现象称为过拟合。而模型在训练集上的拟合效果很差,其在测试集上的拟合效果往往也不会理想,这种现象成为欠拟合。事实表明,这一结果与模型的复杂性以及数据集的大小有密切的关系。模型过于简单,导致模型缺乏足够的表达能力,会导致欠拟合;而模型过于复杂,则会导致模型与训练集的数据之间有较强的贴合性,模型的指向性太强,从而造成较差的泛化效果;一般来说,随着训练数据量的增加,泛化能力会提升。
所以,在机器学习中,我们通常要在评估几个候选模型的效果后选择最佳的模型。有时,这些模型本质上就是不同的机器学习方法,例如MLP与决策树。有时,是对于同一个基本模型,比较其在不同参数设置下的效果,例如在训练MLP时,我们尝试比较不同的隐藏层层数,隐藏层单元数量,学习率,批量大小以及不同激活函数的设置下,模型的测试效果。
为了说明这一过程,下面以多项式的回归为例进行阐述。
二、多项式回归
1.引入库
代码如下:
import math
import numpy as np
import torch
from torch import nn
from d2l import torch as d2l2.生成数据集
给定x,我们用如下三次多项式来生成数据集的标签。
其中
真实的数据总是存在各种噪声,它可能源于观偏差测,环境等。所以我们需要添加一个扰动项
此处,各项的系数除以阶乘项的目的是防止由于大阶数的指数项项造成求导后的梯度很大,这往往不利于优化函数的收敛。
训练集和测试集的数量设为100。
样本:
阶数:
系数项(权重项):
我们的数据集产生于三阶多项式,但真实情况下我们是无法预知数据点的函数关系的。如果我们采用多项式回归的方式来拟合数据,那么用来训练的模型可能是更高阶的函数。所以在此处我们可以把多项式的最大阶数设置得大一点,给我们后续的尝试留有足够的空间。
代码如下:
max_degree = 20 # 多项式的最大阶数
n_train, n_test = 100, 100 # 训练和测试数据集大小
true_w = np.zeros(max_degree) # 分配大量的空间
true_w[0:4] = np.array([5, 1.2, -3.4, 5.6])
features = np.random.normal(size=(n_train + n_test, 1))
np.random.shuffle(features)
poly_features = np.power(features, np.arange(max_degree).reshape(1, -1))
for i in range(max_degree):
poly_features[:, i] /= math.gamma(i + 1) # gamma(n)=(n-1)!
# labels的维度:(n_train+n_test,)
labels = np.dot(poly_features, true_w)
labels += np.random.normal(scale=0.1, size=labels.shape)3.定义模型的评估函数
采用MSE损失函数,单层线性网络(它本质可以看成一个多元线性回归问题)
参数设置:

def evaluate_loss(net, data_iter, loss): #@save
"""评估给定数据集上模型的损失"""
metric = d2l.Accumulator(2) # 损失的总和,样本数量
for X, y in data_iter:
out = net(X)
y = y.reshape(out.shape)
l = loss(out, y)
metric.add(l.sum(), l.numel())
return metric[0] / metric[1]4.训练函数
def train(train_features, test_features, train_labels, test_labels,
num_epochs=400):
loss = nn.MSELoss(reduction='none')
input_shape = train_features.shape[-1]
# 不设置偏置,因为我们已经在多项式中实现了它
net = nn.Sequential(nn.Linear(input_shape, 1, bias=False))
batch_size = min(10, train_labels.shape[0])
train_iter = d2l.load_array((train_features, train_labels.reshape(-1,1)),
batch_size)
test_iter = d2l.load_array((test_features, test_labels.reshape(-1,1)),
batch_size, is_train=False)
trainer = torch.optim.SGD(net.parameters(), lr=0.01)
animator = d2l.Animator(xlabel='epoch', ylabel='loss', yscale='log',
xlim=[1, num_epochs], ylim=[1e-3, 1e2],
legend=['train', 'test'])
for epoch in range(num_epochs):
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
if epoch == 0 or (epoch + 1) % 20 == 0:
animator.add(epoch + 1, (evaluate_loss(net, train_iter, loss),
evaluate_loss(net, test_iter, loss)))
print('weight:', net[0].weight.data.numpy())5.模型测试
模型1:三阶多项式函数
# 从多项式特征中选择前4个维度,即1,x,x^2/2!,x^3/3!
train(poly_features[:n_train, :4], poly_features[n_train:, :4],
labels[:n_train], labels[n_train:])
plt.show()模型2:线性函数
# 从多项式特征中选择前2个维度,即1和x
train(poly_features[:n_train, :2], poly_features[n_train:, :2],
labels[:n_train], labels[n_train:])
plt.show()模型3:高阶函数
# 从多项式特征中选取所有维度
train(poly_features[:n_train, :], poly_features[n_train:, :],
labels[:n_train], labels[n_train:], num_epochs=1500)
plt.show()总结
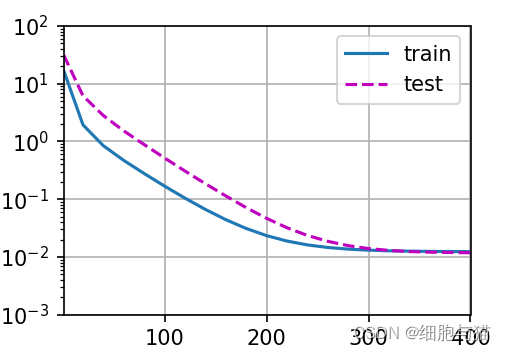
三个模型的结果显示:线性模型过于简单,误差在训练早期就无法降低,模型在测试集与训练集上的误差都维持在一个较高的水平,模型是欠拟合的;高阶函数则过于复杂,导致模型出现过拟合;综合来看,三阶函数是相对较优的模型,这也符合数据集真实的情况。
值得注意的是,由于数据的选取存在随机性,所以每次程序运行得到的误差图像也有所不同,甚至有可能高阶函数的模型的表现更好。
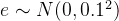
![X=\left [ x_{1},x_{2}...x_{200} \right ]^\top_{200\times 1}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT9YJTNEJTVDbGVmdCUyMCU1QiUyMHhfJTdCMSU3RCUyQ3hfJTdCMiU3RC4uLnhfJTdCMjAwJTdEJTIwJTVDcmlnaHQlMjAlNUQlNUUlNUN0b3BfJTdCMjAwJTVDdGltZXMlMjAxJTdE)
![\left [ 5,1.2,-3.4,5.6,0\cdots 0 \right ]](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUNsZWZ0JTIwJTVCJTIwNSUyQzEuMiUyQy0zLjQlMkM1LjYlMkMwJTVDY2RvdHMlMjAwJTIwJTVDcmlnaHQlMjAlNUQ%3D)