(CART)回归树

1.基本概念

CART树全名叫做分类回归树，它既可以用于分类还可以用于回归，这里主要讲解回归树。回归树从字面上理解就是使用树模型来做回归问题。

在CART回归树中，每一个叶子节点都输出一个该叶子节点中包含所有的数据样本的均值作为预测值。
$$c_m=ave(yi|lea{f}_m)(1.1)$$
在线性回归问题中定义了均方误差来衡量预测值与实际值的差距，在这里使用总方差来衡量预测值与实际值的差距，这里选用方差衡量的原因，方差是数据序列与均值的关系，而均方误差是数据序列与真实值之间的关系。所以这里的回归问题就是构造回归树，使方差值最小
$$min\sum _{i=1}^m(f(x_i)-y_i{)}^2(1.2)$$
要最小化CART树的方差，就必须最小化左子树和右子树的方差之和，要最小化左右子树的方差之和就将问题等价于构造CART树过程中选择最佳的划分特征和特征值使得左右子树的方差之和最小。

在解决这个问题上，这里两层遍历所有特征维度和特征值，选择出使左右子树方差最小的划分特征特征维度和特征值，并将数据集根据划分特征维度和特征值一分为二
D 1 { j , s } = { x ∣ x ( j ) ≤ s } D 2 { j , s } = { x ∣ x ( j ) > s } ( 1.3 ) D_1\{j,s\}=\{x|x^{(j)}\leq s\}\\ D_2\{j,s\}=\{x|x^{(j)}> s\}\quad\quad\quad(1.3) D1​{j,s}={x∣x(j)≤s}D2​{j,s}={x∣x(j)>s}(1.3)
划分后的总方差
m i n ( j , s ) { m i n ∑ x i ∈ D 1 { j , s } ( y i − c 1 ) 2 + m i n ∑ x i ∈ D 2 { j , s } ( y i − c 2 ) 2 } ( 1.4 ) min_{(j,s)}\{min\sum_{x_i\in D_1\{j,s\}}(y_i-c_1)^2+min\sum_{x_i\in D_2\{j,s\}}(y_i-c_2)^2\}\quad(1.4) min(j,s)​{minxi​∈D1​{j,s}∑​(yi​−c1​)2+minxi​∈D2​{j,s}∑​(yi​−c2​)2}(1.4)
选择最佳划分特征维度和特征值伪代码：

对每一个特征维度：
	对每一个特征维度：
		将数据集划分为两份
		计算划分后的总误差
		如果划分后的总误差小于当前最小误差，那么将更新最小误差并存储特征维度和特征值
返回最佳划分特征维度和特征值

2.树回归代码实现

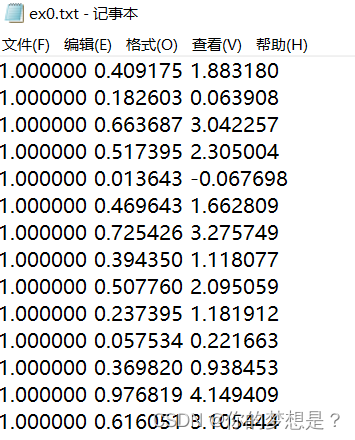
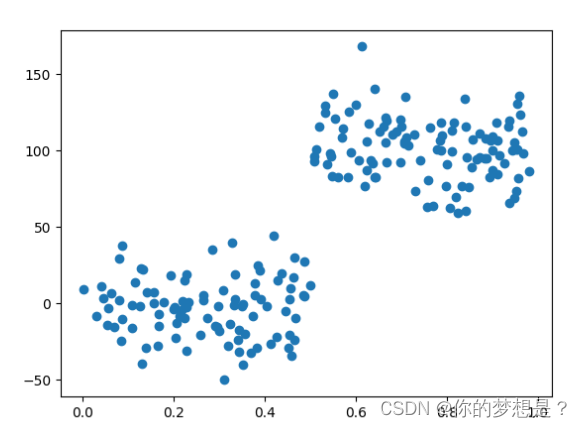
数据集中有三个特征维度

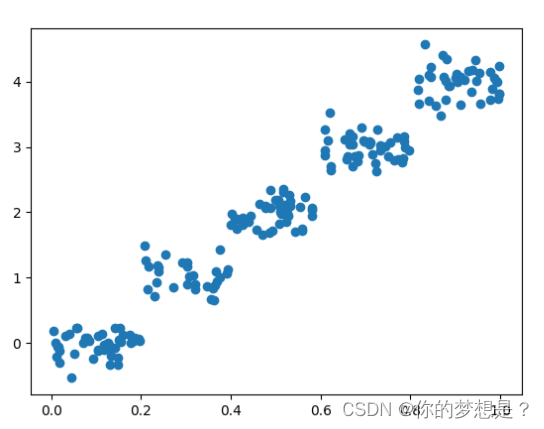
绘制散点图数据分析

树回归代码实现

#导入第三方科学计算包
from numpy import *
#导入matplotlib第三方绘图库
import matplotlib.pyplot as plt
#导入绘制树
import treePlotter as plt_tree
#将文本文件转换为数据集
def loadDataSet(fileName):
    dataMat=[]
    f=open(fileName)
    for line in f.readlines():
        curLine=line.strip().split('\t')
        #将每行映射为浮点数类型
        fltLine=list(map(float,curLine))
        dataMat.append(fltLine)
    return dataMat
#创建叶节点
def regLeaf(dataSet):
    #计算出类别标签的均值
    return mean(dataSet[:,-1])
#计算总方差
def regErr(dataSet):
    #根据类别标签的方差预测估计样本总方差
    return var(dataSet[:,-1])*shape(dataSet)[0]
#将数据集按照特征值进行切分
def binSplitDataSet(dataSet,feature,value):
    #根据数据集与特征值的比较将数据集划分为两个切片
    mat0=dataSet[nonzero(dataSet[:,feature]>value)[0],:]
    mat1=dataSet[nonzero(dataSet[:,feature]<=value)[0],:]
    return mat1,mat0
#树构建函数
def createTree(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
    #寻找最佳划分维度及特征值
    feat,value=chooseBestSplit(dataSet,leafType,errType,ops)
    #如果没有找到最佳特征值，返回叶子节点的值
    if feat==None:
        return value
    retree={}
    retree['spInd']=feat
    retree['spVal']=value
    lSet,rSet=binSplitDataSet(dataSet,feat,value)
    retree['left']=createTree(lSet,leafType,errType,ops)
    retree['right']=createTree(rSet,leafType,errType,ops)
    return retree
#寻找数据集最佳切分位置
def chooseBestSplit(dataSet,leafType=regLeaf,errType=regErr,ops=(1,4)):
    #获取用户自定义的误差减小最小值和切分后数据集样本最少数目
    tolS=ops[0]
    tolN=ops[1]
    #如果数据集中的所有样本的类都一样则无需切分，直接创建叶子节点
    if len(set(dataSet[:,-1].T.tolist()[0]))==1:
        return None,leafType(dataSet)
    m,n=shape(dataSet)
    #获取样本的总方差
    S=errType(dataSet)
    #定义并初始化最佳划分后的总方差
    bestS=inf
    #定义并初始化最佳划分的特征维度
    bestIndex=0
    #定义并初始化最佳划分的特征值
    bestValue=0
    #跌倒所有特征维度寻找最佳划分特征维度
    for featIndex in range(n-1):
        #迭代所有特征值，寻找最佳划分特征值
        for splitVal in set(dataSet[:,featIndex].T.tolist()[0]):
            #获取根据特征值划分后的两个数据集
            mat0,mat1=binSplitDataSet(dataSet,featIndex,splitVal)
            #如果经过划分之后数据集中的样本数目低于限定的最少样本数，则放弃该划分方法
            if (shape(mat0)[0]<tolN) or (shape(mat1)[0]<tolN):continue
            #计算通过划分之后样本的总方差值
            newS=errType(mat0)+errType(mat1)
            #根据每次迭代划分的样本总方差来决定选择最佳划分方法
            if newS<bestS:
                #给最佳划分方法信息赋值
                bestIndex=featIndex
                bestValue=splitVal
                bestS=newS
    #如果经过最佳切分后误差减小低于限定最低误差减少值则无需切分，直接创建叶子节点
    if (S-bestS)<tolS:
        return None,leafType(dataSet)
    mat0,mat1=binSplitDataSet(dataSet,bestIndex,bestValue)
    #如果经过最佳切分后数据集中样本数目低于最少限定样本数目则无需切分，直接创建叶子节点
    if (shape(mat0)[0]<tolN) or (shape(mat1)[0]<tolN):
        return None,leafType(dataSet)
    return bestIndex,bestValue

#打印散点图
def pltor(x,y):
    #绘图
    print(x)
    plt.scatter(x.tolist(),y.tolist())
    #展示图
    plt.show()
#测试
if __name__=='__main__':
    myDat=loadDataSet("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch09/ex0.txt")
    print(myDat)
    x=mat(myDat)[:,1]
    y=mat(myDat)[:,-1]

    #绘制散点图
    pltor(x,y)
    tree=createTree(mat(myDat))
    # 绘制树
    plt_tree.createPlot(tree)
    print(tree)

绘制树代码

#导入matplotlb画图包
import matplotlib.pyplot as plt
from numpy import *

descisionNode=dict(boxstyle="sawtooth",fc="0.8")
leafNode=dict(boxstyle="round4",fc="0.8")
arrow_args=dict(arrowstyle="<-")
ax=None
totalW=0
totalD=0
xOff=None
yOff=None

#绘制带箭头的注解
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
    ax.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext=centerPt,textcoords='axes fraction',\
    va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)


#获取叶子节点的数目和树的层次
def getNumLeafs(myTree):
    numLeafs=0
    left_Leafs = 0
    right_Leafs=0
    left_Tree=myTree['left']
    if type(left_Tree).__name__=='dict':
        left_Leafs+=getNumLeafs(left_Tree)
    else:
        left_Leafs+=1
    right_Tree = myTree['right']
    if type(right_Tree).__name__ == 'dict':
        right_Leafs += getNumLeafs(right_Tree)
    else:
        right_Leafs+=1
    numLeafs=right_Leafs+left_Leafs
    return numLeafs
#获取树的层次
def getTreeDepth(myTree):
    maxDepth=0
    right_Depth = 0
    left_Depth = 0
    left_Tree = myTree['left']
    if type(left_Tree).__name__ == 'dict':
        left_Depth =1+ getTreeDepth(left_Tree)
    else:
        left_Depth = 1
    right_Tree = myTree['right']
    if type(right_Tree).__name__ == 'dict':
        right_Depth =1+ getTreeDepth(right_Tree)
    else:
        right_Depth = 1
    if left_Depth>=right_Depth:
        maxDepth=left_Depth
    else:
        maxDepth=right_Depth
    print(f"左树的深度为{left_Depth},右树的深度为{right_Depth}")
    return maxDepth

#在分支上显示基于特征值划分判断值
def plotMidText(cntrPt,parentPt,txtString):
    xMid=(parentPt[0]-cntrPt[0])/2.0+cntrPt[0]
    yMid=(parentPt[1]-cntrPt[1])/2.0+cntrPt[1]
    ax.text(xMid,yMid,txtString)
#绘制决策树的节点
def plotTree(myTree,parentPt,nodeTxt):
    global yOff
    global xOff
    numLeafs=getNumLeafs(myTree)
    depth=getTreeDepth(myTree)
    firstStr='划分维度是：'+str(myTree['spInd'])+'划分特征值是:'+str(myTree['spVal'])
    cntrPt=(xOff+float(1+float(numLeafs))/2.0/totalW,yOff)
    plotMidText(cntrPt,parentPt,nodeTxt)
    plotNode(firstStr,cntrPt,parentPt,descisionNode)
    left_tree=myTree['left']
    right_tree=myTree['right']
    yOff=yOff-1.0/totalD
    if type(left_tree).__name__=='dict':
        plotTree(left_tree,cntrPt,'<=')
    else:
        xOff=xOff+1.0/totalW
        plotNode(left_tree,(xOff,yOff),cntrPt,leafNode)
        plotMidText((xOff,yOff),cntrPt,"<=")
    if type(right_tree).__name__=='dict':
        plotTree(left_tree,cntrPt,'>')
    else:
        xOff=xOff+1.0/totalW
        plotNode(left_tree,(xOff,yOff),cntrPt,leafNode)
        plotMidText((xOff,yOff),cntrPt,">")
    yOff=yOff+1/totalD
#绘制决策树
def createPlot(inTree):
    plt.rcParams['font.sans-serif']=['SimHei']
    plt.rcParams['axes.unicode_minus']=False
    fig=plt.figure(1,facecolor='white')
    fig.clf()
    axprops=dict(xticks=[],yticks=[])
    global ax
    ax=plt.subplot(111,frameon=False,**axprops)
    global totalW
    totalW=float(getNumLeafs(inTree))
    global totalD
    if(type(inTree["left"]).__name__=='dict' or type(inTree["right"]).__name__=='dict' ):
        totalD=float(getTreeDepth(inTree))-1
    else:
        totalD=1
    print(totalD)
    global xOff
    xOff=-0.5/totalW
    global yOff
    yOff=1.0
    plotTree(inTree,(0.5,1.0),'')
    plt.show()

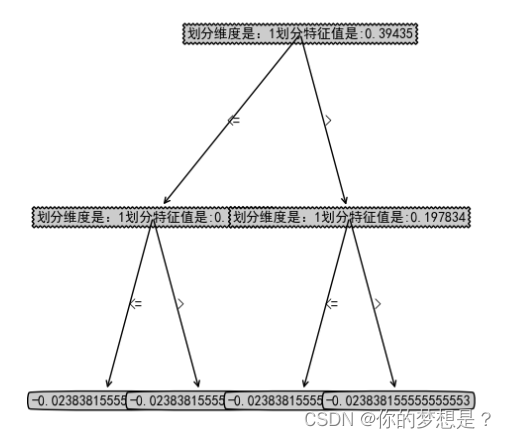
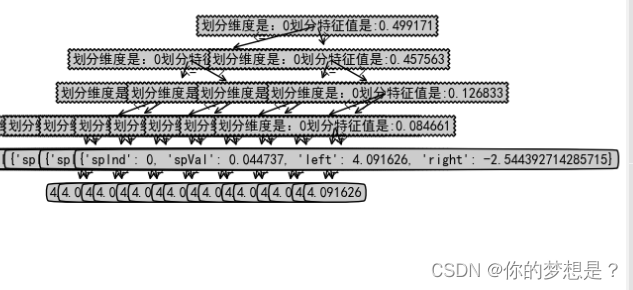
树模型

3.对树进行剪枝

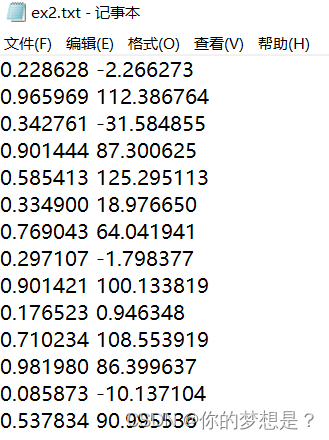
这里有一份数据集

好像从数据集特征维度和散点图上好像是很简单很普通的数据集，但是通过上面树回归代模型来对对这个数据集做树回归

通过这个树发现太多叶子节点了，出现了过拟合现象，这是为什么呢？原因在于上面的模型在创建树的停机条件ops默认为（1，4），解释下ops第一个参数是划分后最低误差值，第二个参数是划分后的每个数据集中最少样本数目，所以ops对于样本数据太敏感了。为了预防过拟合现象，这里对树模型进行后剪枝操作

后剪枝实在树模型构建完成之后进行的操作，主要流程：如果合并后的叶子节点误差比为合并的叶子节点误差值要小，那就选择合并叶子节点

伪代码

基于已有的树切分测试数据：
	如果存在任一子集是一颗树，则在该子集递归剪枝过程
	计算将当前两个叶子节点合并后的误差
	计算不合并的误差
	如果合并和后的误差小于不合并的误差，合并叶子节点

代码实现

#导入科学计算包
from numpy import *
#导入树回归算法
import 将CART算法用于树回归 as algriothm
#导入绘制树
import treePlotter as plt_tree
#判断输入变量是否是一颗数
def isTree(obj):
    return (type(obj).__name__=='dict')
#从上向下遍历，找相邻两个叶子节点求平均值
def getMean(tree):
    if isTree(tree['right']):
        tree['right']=getMean(tree['right'])
    if isTree(tree['left']):
        tree['left']=getMean(tree['left'])
    return (tree['left']+tree['right'])/2
#对树进行后剪枝操作
def prune(tree,testDate):
    #如果测试数据集中没有样本，则返回训练集平均值
    if(shape(testDate)[0])==0:
        return getMean(tree)
    #如果右子树，左子树两者都不是不是叶节点，则对测试数据进行划分
    if (isTree(tree['right']) or isTree(tree['left'])):
        lset,rset=algriothm.binSplitDataSet(testDate,tree['spInd'],tree['spVal'])
    #如果左子树是树，则递归对左子树进行后剪枝操作
    if isTree(tree['left']):
        tree['left']=prune(tree['left'],lset)
    #如果右子树是树，则递归对右子树进行后剪枝操作
    if isTree(tree['right']):
        tree['right']=prune(tree['right'],rset)
    #如果左右子树都是叶子节点，则尝试进行对叶子节点的合并操作
    if not isTree(tree['left']) and not isTree(tree['right']):
        #将测试数据集进行划分
        lset,rset=algriothm.binSplitDataSet(testDate,tree['spInd'],tree['spVal'])
        #计算没有合并的错误率
        errorNoMerge=sum(power(lset[:,-1]-tree['left'],2))+sum(power(rset[:,-1]-tree['right'],2))
        #对叶子节点进行合并
        treeMean=(tree['left']+tree['right'])/2.0
        #计算合并后的错误率
        errorMerge=sum(power(testDate[:,-1]-treeMean,2))
        #若合并后的错误率低于未合并的错误率，则进行合并，否则不合并
        if errorMerge<errorNoMerge:
            # print("合并")
            return treeMean
        else:
            return tree
    return tree
 #测试
if __name__ == '__main__':
     myDat =algriothm.loadDataSet("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch09/ex2.txt")
     testDat=algriothm.loadDataSet("D:/学习资料/机器学习实战/《机器学习实战》源代码/machinelearninginaction/Ch09/ex2test.txt")
     tree=algriothm.createTree(mat(myDat))
     testTree=prune(tree,mat(testDat))
     plt_tree.createPlot(testTree)
     # print(testTree)

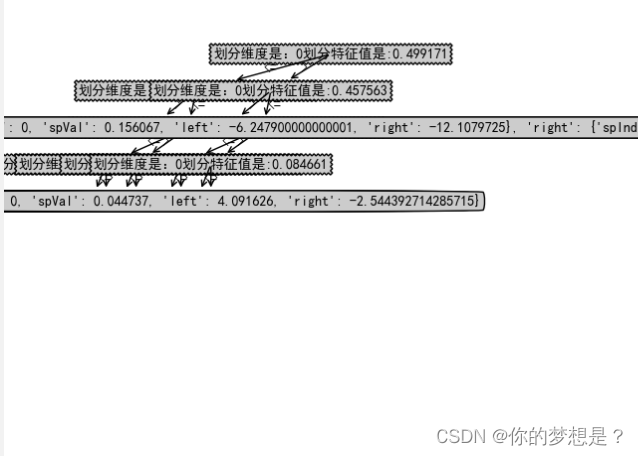
经过后剪枝后

记过后剪枝后叶子节点数目缺失有减少

预剪枝：在最开始的树回归中就有运用到预剪枝操作，提前终止条件就是一种所谓的预剪枝操作，它是在构建模型树的过程中进行的，这种操作能够避免欠拟合。

4.总结

CART回归树是使用方差来衡量预测值与实际值的，对树模型构建过程中，为了避免过拟合可以使用后剪枝操作。

参考博客：回归树（Regression Tree） - wuliytTaotao - 博客园 (cnblogs.com)

参考书籍：《机器学习实战》