Bootstrap

图论 - 临接矩阵与临接表介绍与分析对比

图

前言

图的力扣什么的也刷了也不少了,但是刷的时候吧老是觉得想法比较杂乱,不成章法,对此我痛定思痛,觉得是时候花时间来系统的捋一捋关于图的一些内容,文章估计比较长,如果你是初学的朋友估计会有点吃力,不过加油肯定能学会的.

图论数据结构

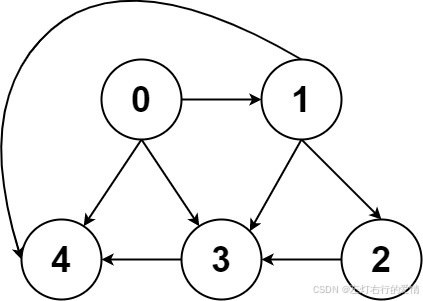
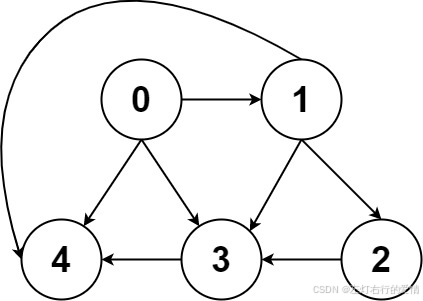
对于图的逻辑结构是很简单的,如下
在这里插入图片描述
可以看到是由节点(Vertex)+边(Edge)构成.
它的代码实现也很简单,你可以参考着多叉树来看:

// 图节点的逻辑结构
class Vertex {
    int id;
    Vertex[] neighbors;
}

// 基本的 N 叉树节点
class TreeNode {
    int val;
    TreeNode[] children;
}

树的DFS/BFS遍历都适用于图.
但是图比树多了一个概念-- 度(degree).
度是每个节点相连边的条数.
每个节点的度被细分为入度(indegree)与出度(outdegree).
上图的节点 3 的入度为 3（有三条边指向它），出度为 1（它有 1 条边指向别的节点）。

上面图结构是逻辑上这样实现,但是我们很少会用Vertex类,而是用邻接表和邻接矩阵来实现图结构.

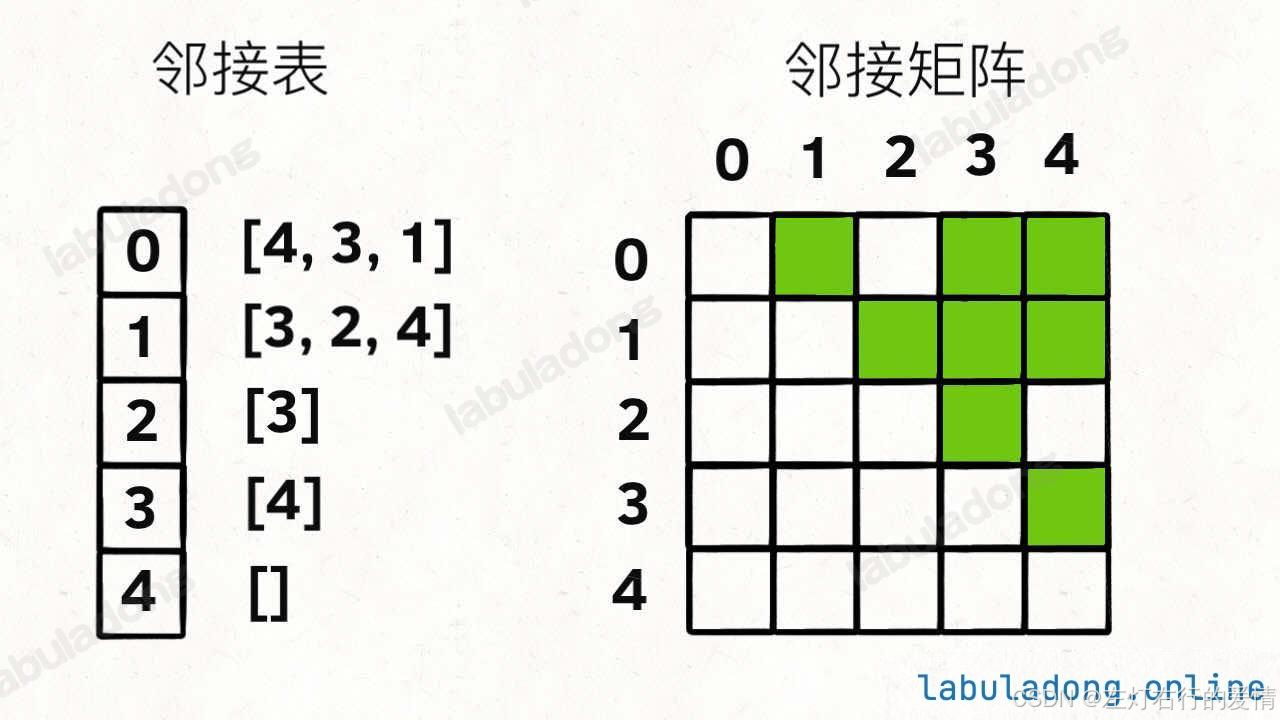
邻接表与临接矩阵

在这里插入图片描述
在这里插入图片描述
上面的图很直观的表示出来了它们的区别.
我先给出它们的实现

// 邻接表
// graph[x] 存储 x 的所有邻居节点
List<Integer>[] graph;


// 邻接矩阵
// matrix[x][y] 记录 x 是否有一条指向 y 的边
boolean[][] matrix;
邻接表

在学习邻接表时，我们会看到 List[] 这样的数据结构，刚开始可能会觉得很奇怪，不明白为什么要这样写。尤其是看到邻接表的示意图时，可能会误以为“链表相连，链表里面是数组”，但实际上并不是这样。
如果我们仔细分析 List[]，可以拆解成两个部分：

  • 它首先是一个数组（[] 说明是数组）。
  • 数组的每个元素都是 List（说明数组存的是列表）。

为什么 List[] 适合表示图的邻接表？

我们先问自己一个问题：在一个图里，哪些数据是固定的？哪些是不固定的？

  • 节点的个数是固定的（假设图有 N 个节点，它的编号通常是 0 ~ N-1）。
  • 每个节点的邻接边数是不确定的（比如某个点的出度可能是 2，也可能是 5）。

那么，我们就需要一个既能存固定数量的节点，又能灵活存储每个节点的邻接点的数据结构：

  1. 数组适合存固定数量的节点
    既然节点数是固定的，我们就可以用数组来存储所有节点。
    例如 List[] graph = new ArrayList[N];，表示有 N 个节点，每个节点都有一个 List 来存邻接点。
  2. 列表（List）适合存每个节点的不定邻居
    由于每个节点的邻接点数量不同，我们不能用固定大小的数组存储邻接点，而链表（List）的动态特性完美地解决了这个问题。
//举个例子:
graph[0] = new ArrayList<>(Arrays.asList(1, 2)); // 0 号节点连向 1 和 2
graph[1] = new ArrayList<>(Collections.singletonList(3)); // 1 号节点连向 3

List[] 既有数组的优势，又有链表的灵活性，非常适合表示图的邻接表.

邻接矩阵

我们可以看到是二维数据存储图,这种给人的感觉是力大砖飞,存储空间巨大,查询O(1),而且有向,无向图,有权,无权图都可以表示.
且二维数据也比较容易上手,一般学到图的也都有些了解,比较亲民的类型.
它的特点:

邻接矩阵的特点
特点分析
存储空间O(N^2)，如果 N 很大且边较少，会浪费大量内存
查询边O(1)，直接访问 graph[i][j]
添加边O(1)，只需 graph[i][j] = 1 / weight
删除边O(1)，只需 graph[i][j] = 0 / INF
遍历邻接点O(N)，需要扫描整行 graph[i][*]
适用于稠密图（边的数量接近 N^2）
适用算法总结
算法邻接矩阵是否适合？理由
BFS / DFS❌ 不适合遍历邻接点太慢 O(N)
Dijkstra（最短路径）✅ 适合O(N^2) 适用于 小规模 图
Floyd-Warshall（全源最短路）✅ 适合O(N^3) 适用于 稠密图
Kruskal（最小生成树）❌ 不适合需要转换成边列表
Prim（最小生成树）✅ 适合O(N^2) 适用于 小规模 图
拓扑排序❌ 不适合需要遍历所有出边
什么时候用邻接矩阵？
  • ✅ 当 M ≈ N^2（稠密图）时，存储邻接矩阵更合适。
  • ✅ 当查询两点是否相连的次数特别多时，邻接矩阵更高效 O(1)。
  • ✅ 当使用 Floyd-Warshall、Prim（O(N^2)）等基于矩阵运算的算法时，邻接矩阵更合适。
什么时候不用邻接矩阵？
  • ❌ 当 M ≪ N^2（稀疏图）时，邻接矩阵浪费空间。
  • ❌ 当需要频繁遍历某个点的邻接点时，邻接表更高效。
  • ❌ 当使用 BFS / DFS / Dijkstra / Kruskal 等以遍历为主的算法时，邻接表更合适。
临接表
邻接表的特点
特点分析
存储空间O(N + M)，只存储实际存在的边，适合 稀疏图
查询边O(deg(i))，需遍历 List[i] 查找
添加边O(1)，直接 list[i].add(j)
删除边O(deg(i))，需遍历 List[i] 删除
遍历邻接点O(deg(i))，比邻接矩阵快
适用于稀疏图（边的数量远小于 N^2）
适用算法总结
算法邻接表是否适合？理由
BFS / DFS✅ 适合访问邻接点更快 O(deg(i))
Dijkstra（最短路径）✅ 适合使用 优先队列 + 邻接表 实现 O(M logN)
Floyd-Warshall（全源最短路）❌ 不适合需要 O(N^2) 矩阵操作
Kruskal（最小生成树）✅ 适合本质是边列表，可直接排序
Prim（最小生成树）✅ 适合使用 优先队列 + 邻接表 实现 O(M logN)
拓扑排序✅ 适合存出度更方便，遍历所有出边 O(M)
什么时候用邻接表？
  • ✅ 当 M ≪ N^2（稀疏图）时，邻接表更节省空间。
  • ✅ 当频繁遍历某个点的邻接点时，邻接表更高效。
  • ✅ 当使用 BFS / DFS / Dijkstra（堆优化）等遍历为主的算法时，邻接表更合适。
什么时候不用邻接表？
  • ❌ 当 M ≈ N^2（稠密图）时，邻接表存储边的指针会浪费额外空间。
  • ❌ 当查询两点是否相连的次数特别多时，邻接表查找 O(deg(i)) 比邻接矩阵 O(1) 慢。
  • ❌ 当使用 Floyd-Warshall 这种基于矩阵运算的算法时，邻接表不适合。
临接表VS临接矩阵

那我们该如何选择用哪种数据结构去解决问题呢?

取决于边的数量（稀疏 vs. 稠密）
条件适合的数据结构原因
边数接近 N^2（稠密图）邻接矩阵直接用二维数组存储，访问 O(1)，遍历 O(N) 也可接受
边数远小于 N^2（稀疏图）邻接表只存有效边，节省空间，遍历 O(deg(i)) 更高效
取决于执行的操作类型
操作适用的数据结构原因
快速查询两点是否相连✅ 邻接矩阵O(1) 直接查 graph[i][j]
遍历所有邻接点✅ 邻接表O(deg(i))，比邻接矩阵 O(N) 快
快速添加 / 删除边✅ 邻接表O(1) 添加，O(deg(i)) 删除（邻接矩阵删除 O(1) 但空间大）
Dijkstra（最短路径）✅ 邻接表堆优化 Dijkstra O(M logN) 适合 稀疏图
Floyd-Warshall（全源最短路）✅ 邻接矩阵O(N^3)，使用矩阵更高效
Kruskal（最小生成树）✅ 邻接表Kruskal 本质是 边列表，邻接表方便转换
Prim（最小生成树）✅ 邻接表（堆优化） or 邻接矩阵邻接表 + 堆 O(M logN)，邻接矩阵 O(N^2)
BFS / DFS（遍历）✅ 邻接表O(M) 遍历比邻接矩阵 O(N^2) 快
拓扑排序✅ 邻接表存出度方便，遍历 O(M)
选择策略总结
✅ 优先选邻接矩阵的情况
  • 图是稠密图（M ≈ N^2）。
  • 需要快速查询两点是否相连，时间复杂度 O(1)。
  • Floyd-Warshall（O(N^3)）需要矩阵运算。
  • 小规模问题（N < 1000），邻接矩阵 O(N^2) 可以接受。
✅ 优先选邻接表的情况
  • 图是稀疏图（M ≪ N^2）。
  • 主要操作是遍历邻接点（BFS / DFS / Dijkstra / Prim / Kruskal）。
  • Dijkstra（堆优化）或 Prim（堆优化），邻接表 O(M logN) 效率更高。
  • 适用于大规模图（N 很大，M 远小于 N^2）。

图结构的通用代码实现

我们可以抽象出一个 Graph 接口，来实现图的基本增删查改：

interface Graph {
    // 添加一条边（带权重）
    void addEdge(int from, int to, int weight);

    // 删除一条边
    void removeEdge(int from, int to);

    // 判断两个节点是否相邻
    boolean hasEdge(int from, int to);

    // 返回一条边的权重
    int weight(int from, int to);

    // 返回某个节点的所有邻居节点和对应权重
    List<Edge> neighbors(int v);

    // 返回节点总数
    int size();
}

有向加全图

邻接表实现
// 加权有向图的通用实现（邻接表）
class WeightedDigraph {
    // 存储相邻节点及边的权重
    public static class Edge {
        int to;
        int weight;

        public Edge(int to, int weight) {
            this.to = to;
            this.weight = weight;
        }
    }

    // 邻接表，graph[v] 存储节点 v 的所有邻居节点及对应权重
    private List<Edge>[] graph;

    public WeightedDigraph(int n) {
        // 我们这里简单起见，建图时要传入节点总数，这其实可以优化
        // 比如把 graph 设置为 Map<Integer, List<Edge>>，就可以动态添加新节点了
        graph = new List[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new ArrayList<>();
        }
    }

    // 增，添加一条带权重的有向边，复杂度 O(1)
    public void addEdge(int from, int to, int weight) {
        graph[from].add(new Edge(to, weight));
    }

    // 删，删除一条有向边，复杂度 O(V)
    public void removeEdge(int from, int to) {
        for (int i = 0; i < graph[from].size(); i++) {
            if (graph[from].get(i).to == to) {
                graph[from].remove(i);
                break;
            }
        }
    }

    // 查，判断两个节点是否相邻，复杂度 O(V)
    public boolean hasEdge(int from, int to) {
        for (Edge e : graph[from]) {
            if (e.to == to) {
                return true;
            }
        }
        return false;
    }

    // 查，返回一条边的权重，复杂度 O(V)
    public int weight(int from, int to) {
        for (Edge e : graph[from]) {
            if (e.to == to) {
                return e.weight;
            }
        }
        throw new IllegalArgumentException("No such edge");
    }

    // 上面的 hasEdge、removeEdge、weight 方法遍历 List 的行为是可以优化的
    // 比如用 Map<Integer, Map<Integer, Integer>> 存储邻接表
    // 这样就可以避免遍历 List，复杂度就能降到 O(1)

    // 查，返回某个节点的所有邻居节点，复杂度 O(1)
    public List<Edge> neighbors(int v) {
        return graph[v];
    }

    public static void main(String[] args) {
        WeightedDigraph graph = new WeightedDigraph(3);
        graph.addEdge(0, 1, 1);
        graph.addEdge(1, 2, 2);
        graph.addEdge(2, 0, 3);
        graph.addEdge(2, 1, 4);

        System.out.println(graph.hasEdge(0, 1)); // true
        System.out.println(graph.hasEdge(1, 0)); // false

        graph.neighbors(2).forEach(edge -> {
            System.out.println(2 + " -> " + edge.to + ", wight: " + edge.weight);
        });
        // 2 -> 0, wight: 3
        // 2 -> 1, wight: 4

        graph.removeEdge(0, 1);
        System.out.println(graph.hasEdge(0, 1)); // false
    }
}
临接矩阵
import java.util.ArrayList;
import java.util.List;

// 加权有向图的通用实现（邻接矩阵）
public class WeightedDigraph {
    // 存储相邻节点及边的权重
    public static class Edge {
        int to;
        int weight;

        public Edge(int to, int weight) {
            this.to = to;
            this.weight = weight;
        }
    }


    // 邻接矩阵，matrix[from][to] 存储从节点 from 到节点 to 的边的权重
    // 0 表示没有连接
    private int[][] matrix;

    public WeightedDigraph(int n) {
        matrix = new int[n][n];
    }

    // 增，添加一条带权重的有向边，复杂度 O(1)
    public void addEdge(int from, int to, int weight) {
        matrix[from][to] = weight;
    }

    // 删，删除一条有向边，复杂度 O(1)
    public void removeEdge(int from, int to) {
        matrix[from][to] = 0;
    }

    // 查，判断两个节点是否相邻，复杂度 O(1)
    public boolean hasEdge(int from, int to) {
        return matrix[from][to] != 0;
    }

    // 查，返回一条边的权重，复杂度 O(1)
    public int weight(int from, int to) {
        return matrix[from][to];
    }

    // 查，返回某个节点的所有邻居节点，复杂度 O(V)
    public List<Edge> neighbors(int v) {
        List<Edge> res = new ArrayList<>();
        for (int i = 0; i < matrix[v].length; i++) {
            if (matrix[v][i] > 0) {
                res.add(new Edge(i, matrix[v][i]));
            }
        }
        return res;
    }

    public static void main(String[] args) {
        WeightedDigraph graph = new WeightedDigraph(3);
        graph.addEdge(0, 1, 1);
        graph.addEdge(1, 2, 2);
        graph.addEdge(2, 0, 3);
        graph.addEdge(2, 1, 4);

        System.out.println(graph.hasEdge(0, 1)); // true
        System.out.println(graph.hasEdge(1, 0)); // false

        graph.neighbors(2).forEach(edge -> {
            System.out.println(2 + " -> " + edge.to + ", wight: " + edge.weight);
        });
        // 2 -> 0, wight: 3
        // 2 -> 1, wight: 4

        graph.removeEdge(0, 1);
        System.out.println(graph.hasEdge(0, 1)); // false
    }
}

有向无权图

把addEdge的权重参数默认为1即可

无向加权图

无向加权图就等同于双向的有向加权图，所以直接复用上面用邻接表/领接矩阵实现的 WeightedDigraph 类就行了，只是在增加边的时候，要同时添加两条边：

// 无向加权图的通用实现
class WeightedUndigraph {
    private WeightedDigraph graph;

    public WeightedUndigraph(int n) {
        graph = new WeightedDigraph(n);
    }

    // 增，添加一条带权重的无向边
    public void addEdge(int from, int to, int weight) {
        graph.addEdge(from, to, weight);
        graph.addEdge(to, from, weight);
    }

    // 删，删除一条无向边
    public void removeEdge(int from, int to) {
        graph.removeEdge(from, to);
        graph.removeEdge(to, from);
    }

    // 查，判断两个节点是否相邻
    public boolean hasEdge(int from, int to) {
        return graph.hasEdge(from, to);
    }

    // 查，返回一条边的权重
    public int weight(int from, int to) {
        return graph.weight(from, to);
    }

    // 查，返回某个节点的所有邻居节点
    public List<WeightedDigraph.Edge> neighbors(int v) {
        return graph.neighbors(v);
    }

    public static void main(String[] args) {
        WeightedUndigraph graph = new WeightedUndigraph(3);
        graph.addEdge(0, 1, 1);
        graph.addEdge(1, 2, 2);
        graph.addEdge(2, 0, 3);
        graph.addEdge(2, 1, 4);

        System.out.println(graph.hasEdge(0, 1)); // true
        System.out.println(graph.hasEdge(1, 0)); // true

        graph.neighbors(2).forEach(edge -> {
            System.out.println(2 + " <-> " + edge.to + ", wight: " + edge.weight);
        });
        // 2 <-> 0, wight: 3
        // 2 <-> 1, wight: 4

        graph.removeEdge(0, 1);
        System.out.println(graph.hasEdge(0, 1)); // false
        System.out.println(graph.hasEdge(1, 0)); // false
    }
}

结论

🚀 如果图很稀疏（M ≪ N²），或者要遍历（BFS/DFS/最短路），选 🔹 邻接表
⚡ 如果图很稠密（M ≈ N²），或者要频繁查询边权，选 🔸 邻接矩阵
一定要能熟练写出构建图的模版,深刻理解数据结构!!!

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
大华rtsp子码流格式_监控如何直播？这些品牌摄像机Rtsp取流格式必须知道
docker容器监控系统部署
后端存储流程结构的思考
Java集合------LinkedHashMap底层原理
css样式实现一个滑动按钮
关于 -webkit-overflow-scrolling:touch 的小bug
Mojo编程语言:Al开发者的新宠儿
在Ubuntu16.04里安装ROS Kinetic
业务场景 基于mysql+redis的抢红包活动业务场景
私域引流有什么好的方法
;