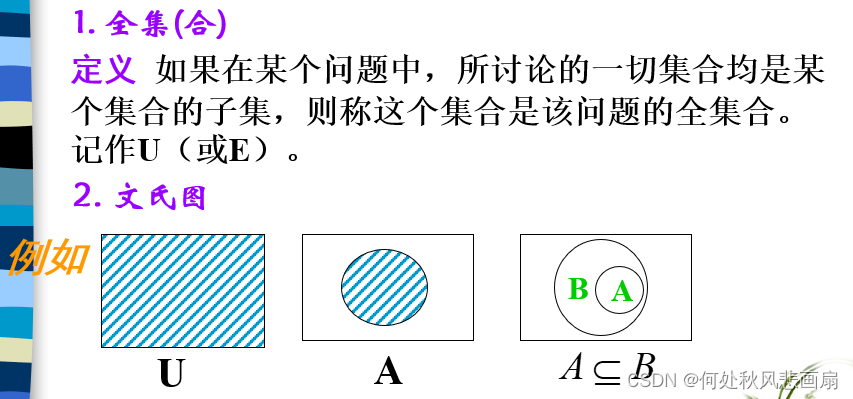
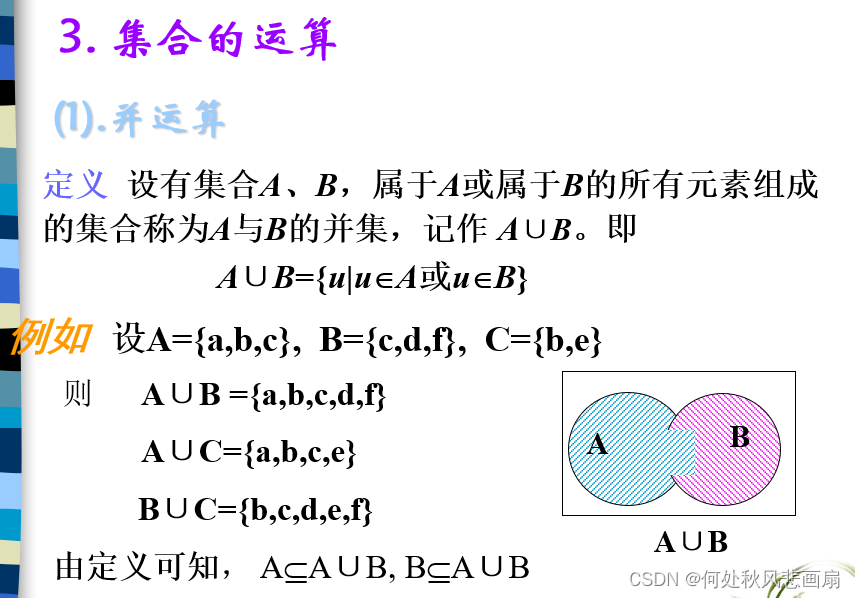
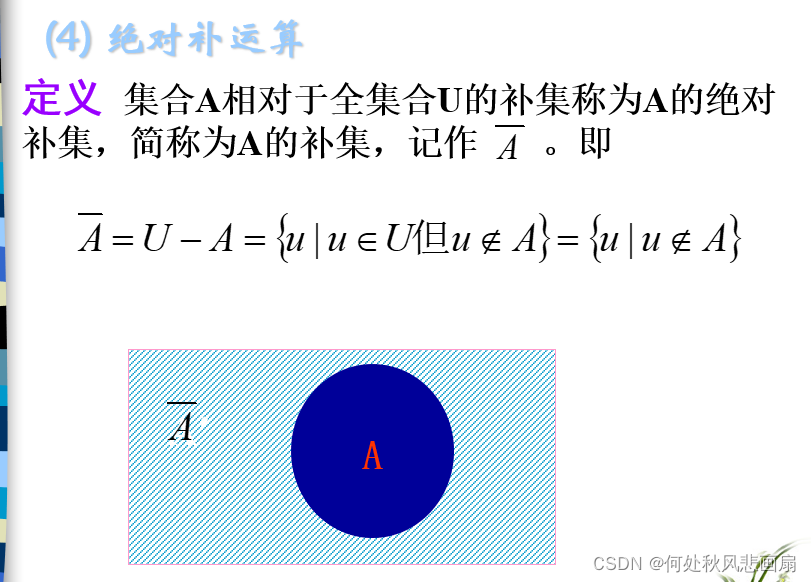
集合
集合及其运算
集合与元素
集合:把一些确定的、彼此不同的事物作为一个整体来看待时,这个整体便称为是一个集合。
元素: 组成集合的那些个体称为集合的元素。
例:全体中国人可组成一个集合,每一个中国人均是这个集合的元素。
通常用大写英文字母来标记集合,用小写英文字母标记组成集合的个体。
若个体a是集合A的元素,则记作“a∈A”。
若个体a不是集合A的元素,则记作“a∉A” 。
几个常用集合的表示符号:
| 符号 | 表示 |
|---|---|
| N | 所有自然数的集合 |
| Nm | 集合{0,1,2,…,m-1} |
| I | 所有整数的集合 |
| I+ | 所有正整数的集合 |
| I- | 所有负整数的集合 |
| P | 所有素数的集合 |
| Q | 所有有理数的集合 |
| C | 所有复数的集合 |
| R | 所有实数的集合 |
| R- | 所有负实数的集合 |
| R+ | 所有正实数的集合 |
集合的表示方法
列举法:按任意顺序逐一列举集合中的元素于花括号内,元素之间用逗号隔开。
例如:A={2,a,b,9},B={4,5,6,7,8}
描述法:给定一个条件P(x),当且仅当个体a使P(a)成立时,a∈A。其一般形式为A={a∣P(a)}。
例如:B={a∣a∈N且4≤a≤8}
集合的基数
集合A中不同元素的个数称为集合A的基数,记作|A|。
例如:上面的|A|=4,|B|=5,集合C有无穷多个元素,因此C的基数是无穷大。
若|A|是有限集,则称A为有限集,否则称A为无限集。
例如 N , I , Q , R 等均为无限集。
空集
不含有任何元素的集合,称为空集,记作∅。
例如 A={x | x∈R 且 x2+8=0 }=∅
集合间的关系
集合的包含和相等是集合间的两个基本关系。
集合的包含
设有集合A、B,如果A的每一个元素都是B的元素,则称A是B的子集,记A⊆B。如果A不是B的子集,则记作A⊄B。
集合的包含关系具有如下几条性质:
1.对任意集合A,∅ ⊆ A ;
2.对任意集合A,A ⊆ A ;
3.对任意集合A、B、C,若 A ⊆ B,B ⊆ C,则 A ⊆ C。
证明性质1:
(反证法)假设 ∅ ⊄ A ,则至少有一个元素 x ∈ ∅ ,但 x ∉ A ,这与空集的定义相矛盾,因此成立。
集合的相等
设有集合A、B,若A ⊆ B且B ⊆ A,则称集合A与B相等,记作A=B。
例如:设A={x | x∈N 且 x能整除24},B={1, 2, 3, 4, 6, 8, 12, 24} ,则 A=B。
集合的真包含
设有集合A、B,若 A ⊆ B , 且A ≠ B,则称A是B的真子集,记作 A ⊂ B ,若A不是B的真子集,则记作 A ⊄ B。
空集的唯一性
空集是唯一的 。
证明:假设有两个空集 ∅1 和 ∅2 ,
因为空集被包含于每一个集合中,
所以有 ∅1 ⊆ ∅2, ∅2 ⊆ ∅1,
由集合的相等性可知,∅1 = ∅2, 故空集是唯一的。
集合的运算和运算定律
幂集
序偶与笛卡尔积
序偶与笛卡尔积
有序n元组
定义:由n个具有给定次序的个体a1,a2,…,an 组成的序列称为有序n元组,记作〈a1,a2,…,an〉。
注意:有序n元组与n个元素的集合,是不相同的。
定义:设〈a1,a2,…,an〉 和〈b1,b2,…,bn〉是两个有序n元组,若 a1=b1, a2=b2, … , an=bn,则称这两个有序n元组相等,并记作 〈a1,a2,…,an〉=〈b1,b2,…,bn〉。
当n=2时,有序二元组〈a,b〉又称为序偶。
笛卡尔积
定义:设A,B为任意集合, A 和 B 的笛卡尔积用A × B 表示,定义为 A × B={〈a,b〉| a ∈ A , b ∈ B }。
笛卡尔积的性质