1. 山脉数组的峰顶索引(852)
题目描述:
算法原理:
根据题意我们可以将数组分为两个部分,一个部分是arr[mid-1]<arr[mid],另一个部分为arr[mid-1]>arr[mid],此时不难发现我们可以将二分查找循环内的条件设置为上述条件,虽然此时会出现mid-1越界的问题,但是完全不用担心,因为left和right下标分别从1和arr.length-2开始的,题目的意思就是山峰是不会出现在0和arr.length-1这两个位置的,所以可以直接跳过。
代码如下:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left = 1, right = arr.length - 2;
while (left < right) {
int mid = left + (right - left + 1) / 2;
if (arr[mid] > arr[mid - 1]) {
left = mid;
} else {
right = mid - 1;
}
}
return left;
}
}
2. 寻找峰值(162)
题目描述:
算法原理:
这一题和第二题是类似的,唯一的不同点在于这一题的峰值可能不为一并且-1下标以及nums.length下标都是假设为负无穷,所以我们的right以及left指针要分别从nums.length-1以及0开始。
这里具有的二段性和上题一致,当arr[mid]>arr[mid-1]时,mid到nums.length-1的区间必有峰,所以left要提到mid的位置,当arr[mid]<arr[mid-1]时,0到mid-1区间内必然有峰,所以right提到mid-1,画图还是比较好理解的。
因为mid必然是大于0的,所以不用去担心越界问题,以及为了防止死循环要给mid计算加一。
代码如下:
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left = 1, right = arr.length - 2;
while (left < right) {
int mid = left + (right - left + 1) / 2;
if (arr[mid] >arr[mid - 1]) {
left = mid;
} else {
right = mid - 1;
}
}
return left;
}
}
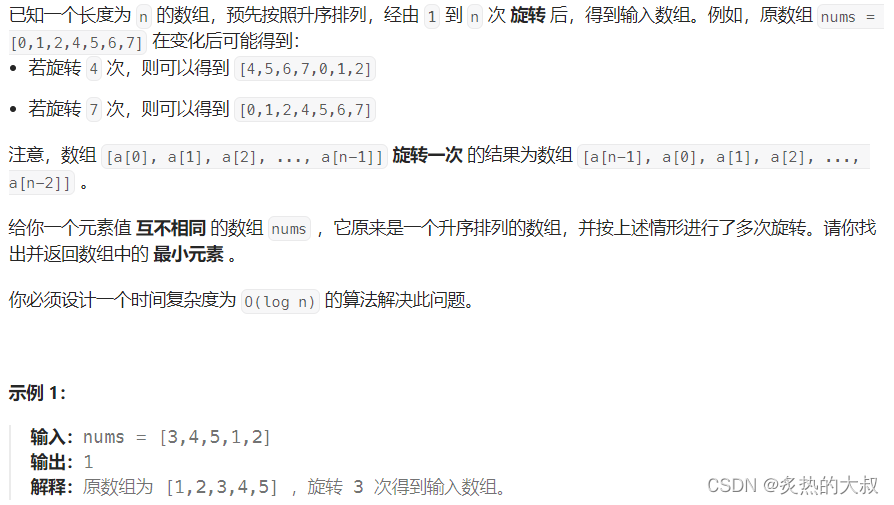
3. 寻找旋转排序数组中的最小值(153)
题目描述:
算法原理:
其实使用二分算法做这类题如果知道并且理解了上一篇博客中的模板的话,剩下来就是分析题目中的二段性,分析完之后直接套模板即可。那么这题的二段性一张图足以描述,如下。
这张图是数组的一种抽象表示,此时y轴就是nums数组的值,x轴就是nums数组的下标,每个旋转后的数组元素大小起伏都是这样的,不难发现对于nums数组的最后一个元素,nums数组的前半部分是严格大于它的,但是nums数组的后半部分都是严格小于它的,由此我们就发现了nums数组的二段性,可以以nums数组的最后一个元素作为基准,具体逻辑如代码所示。
代码如下:
class Solution {
public int findMin(int[] nums) {
int n = nums.length - 1;
int left = 0, right = n;
while (right > left) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[n]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[right];
}
}
4. 点名(LCR 173)
题目描述:
算法原理:
使用二分查找的方法来解决,主要就是要去找到数组中的二段性。根据题目不难发现其中的records数组在没有同学缺席之前,records[i]都是等于i的,在有同学缺席之后records[i]就等于i+1了,这就是数组二段性的体现。还要注意一个细节就是如果数组中缺失的是最后一个数时需要返回数组长度加一。
代码如下:
class Solution {
public int takeAttendance(int[] records) {
int left = 0, right = records.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (records[mid] - mid == 0) {
left = mid + 1;
} else {
right = mid;
}
}
return records[right] == right ? records.length : right;
}
}