原码一位乘法

运算规则：

1，符号位通过对被乘数和乘数的符号位作异或得到，不参与乘法运算。

2，数值部分使用被乘数和乘数的绝对值进行运算。

3，一共要经过n次加法和n次右移位。（n指的是乘数小数点后的位数，即尾数的位数，如 0.1101，小数点后有4位，n就等于4）。

4，移位时进行的是逻辑移位，右移后空出的位置补0。

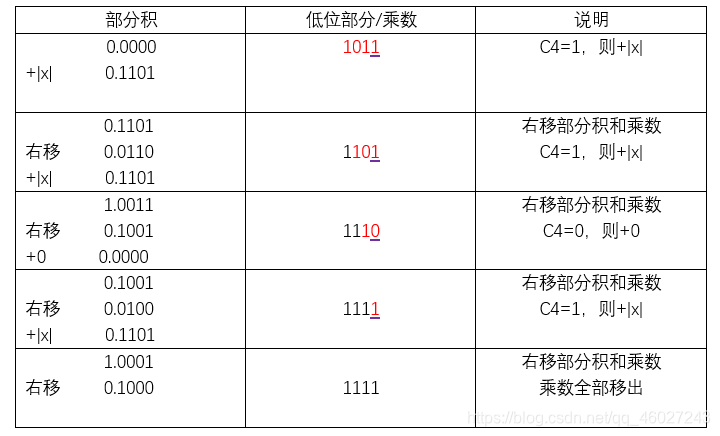
举例说明：

设 x = -0.1101，y = +0.1011，使用原码一位乘法求 x * y。

符号位：p = 1⊕0 = 1；

所以 x * y = 1.10001111。

原码两位乘法

运算规则：

1，符号位通过对被乘数和乘数的符号位作异或得到，不参与乘法运算。

2，数值部分使用被乘数和乘数的绝对值的补码进行运算。移位时进行的是算数移位。

3，部分积和被乘数x均采用三位符号位，乘数末尾会加上一个标志位C，C的初始值为0。

4，运算时乘数的符号位取决于其尾数位数的奇偶性，若尾数的位数是偶数，则使用双符号位，计算时最后一步不移位。若尾数的位数为奇数，则使用单符号位，计算时最后一步要移一位。

如乘数0.0110，尾数有4位，为偶数，所以使用双符号位00.0110；
如乘数0.101，尾数有3位，为奇数，所以使用单符号位0.101。

5，若乘数尾数位数为偶数 n，一共要移位 n/2 次；若乘数尾数位数为奇数 n，则加上最后一次移一位的操作一共要移位 (n+1)/2。

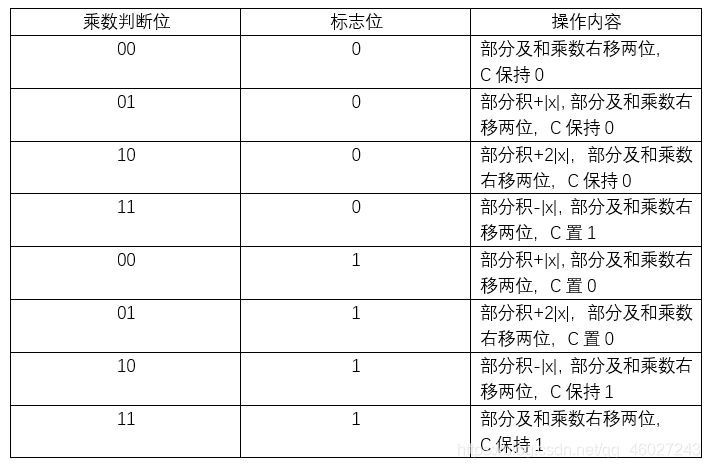
6，运算时每次要判断乘数的后两位和标志位C，根据三位的数值来确定操作内容

判断依据：

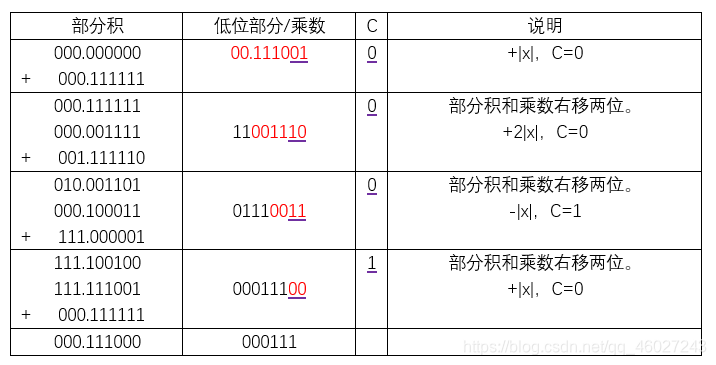
举例说明：

1，设 x = 0.111111，y = -0.111001，使用原码两位乘法求解 [x * y]原码。

|x|补码=0.111111，|y|补码=0.111001，(-|x|)补码=1.000001

符号位：p = 1⊕0 = 1；

所以 [x * y]原码 = 1.111000000111。

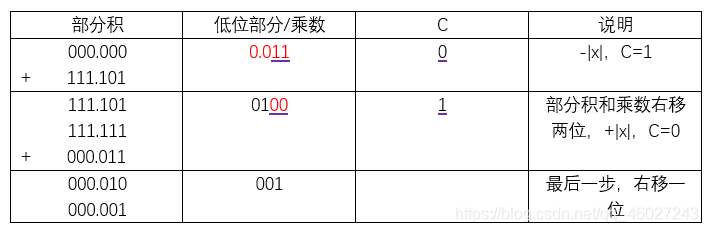
2，设 x = 0.011, y = 0.011，使用原码两位乘法求解 [x * y]原码。

|x|补码 = 0.011，|y|补码 = 0.011，(-|x|)补码 = 1.101。

符号位：p = 0⊕0 = 0；

所以 [x * y]原码 = 0.001001。