C# 实现快速排序

过程拆解

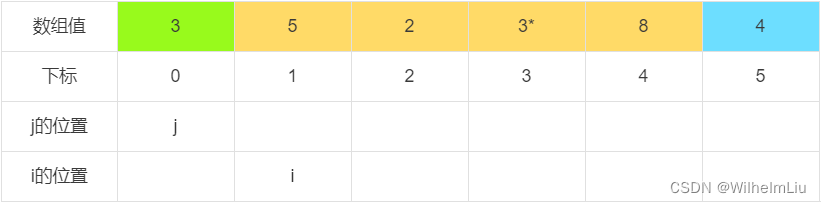
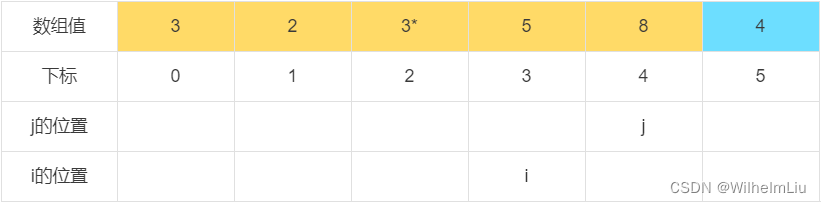
假设现有一数组，如下

基本排序代码，如下

static void Main(string[] args)
{
    int[] array = new int[] { 3, 5, 2, 3, 8, 4 };//替换代码
    int iIndex = BaseSort(array, 0, 5);//替换代码

    for (int i = 0; i < array.Length; i++)
    {
        Console.Write(array[i] + " ");
    }

    Console.WriteLine();
    Console.WriteLine("当前i的下标为" + iIndex);

    Console.ReadKey();
}

public static int BaseSort(int[] array, int start, int end)
{
    int x = array[end];//选取一个判定值(一般选取最后一个)
    int i = start;
    for(int j = start; j < end; j++)
    {
        if(array[j] < x)
        {
            //将下标j的值与下标i的值交换 保证i的前面都小于判定值
            int temp = array[j];
            array[j] = array[i];
            array[i] = temp;
            i++;
        }
    }

    //将下标i的值与判定值交换
    array[end] = array[i];
    array[i] = x;

    return i;
}

1. 将替换代码换成下列代码，运行并分析

int[] array = new int[] { 3, 5, 2, 3, 8, 4 };
int iIndex = BaseSort(array, 0, 5);
//从下标 0 到下标 5 - 1 的元素中找比下标 5 小的值移动到前面，最后将下标i的值与判定值交换

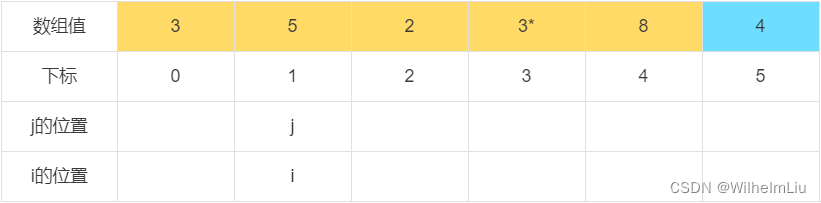
当 j = 0 时，下标为 j 的元素值小于判定值，交换下标 i 与 下标 j 的值，之后 i = i + 1。

当 j = 1 时，下标为 j 的元素值大于判定值。

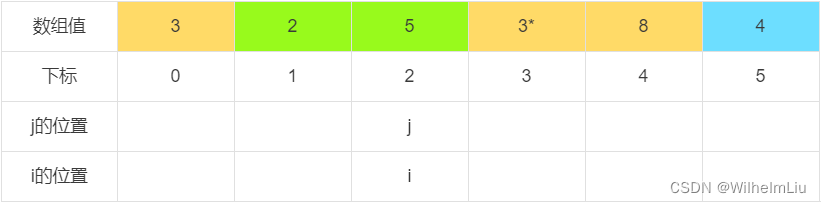
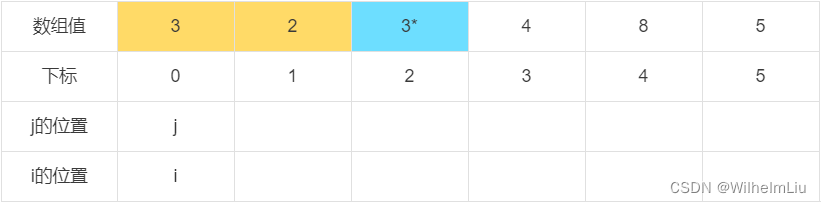
当 j = 2 时，下标为 j 的元素值小于判定值，交换下标 i 与 下标 j 的值，之后 i = i + 1。

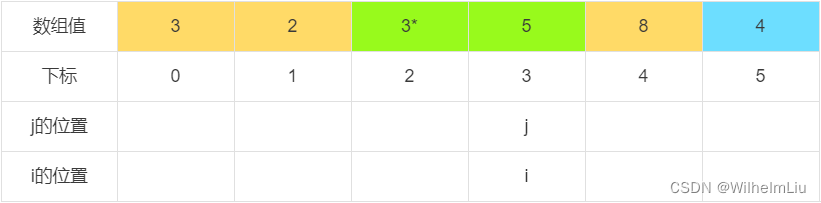
当 j = 3 时，下标为 j 的元素值小于判定值，交换下标 i 与 下标 j 的值，之后 i = i + 1。

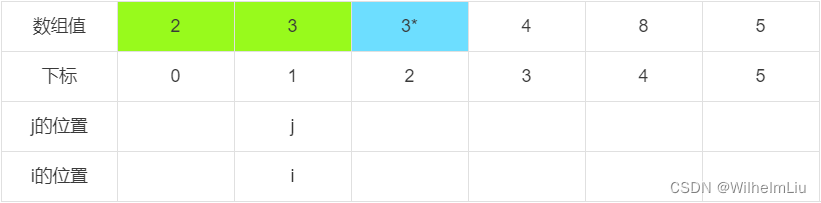
当 j = 4 时，下标为 j 的元素值大于判定值。

当 for 结束循环时，将下标 i 的元素值与判定值交换。

至此，将小于判定值的元素都移动到下标 i 之前，将大于/等于判定值的元素移动到下标i之后。

2. 将替换代码换成下列代码，运行并分析

int[] array = new int[] { 3, 2, 3, 4, 8, 5 };
int iIndex = BaseSort(array, 0, 2);
//从下标 0 到下标 2 - 1 的元素中找比下标 2 小的值移动到前面，最后将下标i的值与判定值交换

当 j = 0 时，下标为 j 的元素值不小于判定值。

当 j = 1 时，下标为 j 的元素值小于判定值，交换下标 i 与 下标 j 的值，之后 i = i + 1。

当 for 结束循环时，将下标 i 的元素值与判定值交换。

至此，将小于判定值的元素都移动到下标 i 之前，将大于/等于判定值的元素移动到下标i之后。

3. 将替换代码换成下列代码，运行并分析

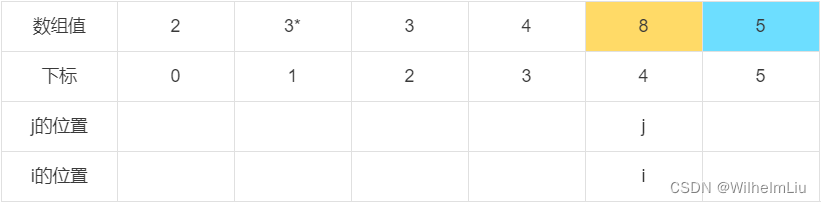
int[] array = new int[] { 2, 3, 3, 4, 8, 5 };
int iIndex = BaseSort(array, 4, 5);
//从下标 4 到下标 5 - 1 的元素中找比下标 5 小的值移动到前面，最后将下标i的值与判定值交换

当 j = 4 时，下标为 j 的元素值大于判定值。

当 for 结束循环时，将下标 i 的元素值与判定值交换。

至此，将小于判定值的元素都移动到下标 i 之前，将大于/等于判定值的元素移动到下标i之后。

算法实现

1. 选择一个数为确定数 (一般为数组最后一个数)，利用分治法放置在确定位置上。
2. 使得小于确定数的元素位于确定位置的左边，大于/等于确定数位于确定位置的右边。
3. 将确定数左边和右边再次进行分治，各自再选择一个数确定在某个位置上。
4. 当分治的数组只有一个元素时，则不需要再次进行分治，可以确定这个数的位置。

代码如下

static void Main(string[] args)
{
    int[] array = new int[] { 3, 5, 2, 3, 8, 4 };
    QuickSort(array, 0, array.Length - 1);

    for (int i = 0; i < array.Length; i++)
    {
        Console.Write(array[i] + " ");
    }

    Console.WriteLine();
    Console.ReadKey();
}

//快速排序
public static void QuickSort(int[] array, int start, int end)
{
    if(start < end)
    {
        int mid = Partition(array, start, end);
        QuickSort(array, start, mid - 1);
        QuickSort(array, mid + 1, end);
    }
}

//分治方法 把数组中一个数放置在确定的位置
public static int Partition(int[] array, int start, int end)
{
    int x = array[end];//选取一个判定值(一般选取最后一个)
    int i = start;
    for(int j = start; j < end; j++)
    {
        if(array[j] < x)
        {
            //将下标j的值与下标i的值交换 保证i的前面都小于判定值
            int temp = array[j];
            array[j] = array[i];
            array[i] = temp;
            i++;
        }
    }

    //将下标i的值与判定值交换
    array[end] = array[i];
    array[i] = x;

    return i;
}

复杂度与稳定性

• 最优时间复杂度：

1. 推导方式：
   每次将数组分为左右数组，每次进行分治时，需要一个 for循环。所以公式为T[ n ] = 2T[ n / 2 ] + n
   第一次迭代 T[ n ] = 2T[ n / 2 ] + n
   第二次迭代 T[ n / 2 ] = 2T[ n / 4 ] + n / 2 推出 T[ n ] = 2{ 2T[ n / 4 ] + n / 2 } + n = 2²T[ n / 2² ] + 2n
   第三次迭代 T[ n / 2² ] = 2T[ n / 8 ] + n / 4 推出 T[ n ] = 2²{ 2T[ n / 8 ] + n / 4 } + 2n = 2³T[ n / 2³ ] + 3n
   第四次迭代 T[ n / 2³ ] = 2T[ n / 16 ] + n / 8 推出 T[ n ] = 2³{ 2T[ n / 16 ] + n / 8 } + 3n = 2⁴T[ n / 2⁴ ] + 4n
   因此，可以推出第m次迭代的时间复杂度 T[ n ] = 2^mT[ n / 2^m ] + mn

   当n = 1时，分治法仅需要进行一次 for循环，所以T[n] = n。
   所以当T[ n / 2^m ] = T[1] 时，即 m = log₂n时
   T[ n ] = 2^mT[ n / 2^m ] + mn = 2^log2nT[1] + (log₂n) * n = n * T[1] + nlog₂n = n + nlog₂n
   所以最优复杂度为 nlog₂n

2. 主定理方式：
   对于公式 T[ n ] = aT[ n / b ] + cn^d ，如果满足 a >= 1，b > 1，d >= 0，则

   满足条件	时间复杂度
   d < logba 即 a > bd	nlogba)
   d = logba 即 a = bd	ndlogn
   d > logba 即 a < bd	nd

   每次将数组分为左右数组，每次进行分治时，需要一个 for循环。所以公式为T[ n ] = 2T[ n / 2 ] + n
   a = 2，b = 2，c = 1，d = 1 得 a = b^d = 2，所以算法复杂度为nlogn

• 最差时间复杂度：当数组全部元素相同时，该算法类似冒泡算法。把最后一个元素放置在最前，之后进行右边数组的排序
• 平均时间复杂度：除数组全部元素相同时，其他情况时间算法复杂度均为nlog₂n
• 空间复杂度：每进行一次迭代需要借助 变量mid ，总共需要进行log₂n次迭代
• 不稳定性：经过选择算法后，后面的数被排在了前面(例如: 3)

因为作者精力有限，文章中难免出现一些错漏，敬请广大专家和网友批评、指正。