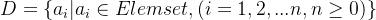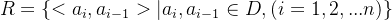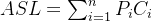1.数据结构C++学习笔记——线性表（顺序储存）

此篇为本人自己学习过程中的笔记，有许多不足之处，仅供参考。

1. 线性表的定义与介绍

2. 线性表的逻辑特征

3. 抽象数据类型线性表的定义

4. 线性表的顺序存储运算以及实现

4.1 下面以C++模版类给出顺序线性表的定义：

4.3.7 获取顺序表元素个数(线性表长度)

4.3.8 获取与i相同的元素在线性顺序表中的位置

4.3.15 若n不是第一个元素，查找第n个元素的前趋

4.3.16 若n不是最后一个元素，查找第n个元素的后继

4.3.17 表合并

5. 顺序储存结构的优缺点

1. 线性表的定义与介绍

● 线性表是是一种线性结构，具有相同特性的数据元素的一个有限序列，数据元素之间的关系是线性。线性表中的数据元素类型可以为简单类型，也可以为复杂类型。

● 数据元素的个数n定义为表的长度，当n=0时，称为空表。

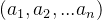
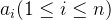
● 将非空的线性表（n>0）记作 $(a_{1},a_{2},...a_{n})$ ，这里的数据元素 $a_{i}(1\leq i\leq n)$ 只是一个抽象的符号，其具体含义在不同的情况下可以不同。

2. 线性表的逻辑特征

● 在非空的线性表中，有且只有一个开始节点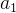 $a_{1}$ ，它没有直接前趋，且只有一个直接后继 $a_{2}$ 。

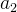
● 有且只有一个终端节点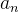 $a_{n}$ ，它没有直接后继，且只有一个直接前趋 $a_{n-1}$ 。

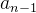
● 其余的内部节点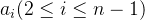 $a_{i}(2\leq i\leq n-1)$ 都有且仅有一个直接前趋 $a_{i-1}$ ，一个直接后继 $a_{i+1}$ 。

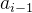
3. 抽象数据类型线性表的定义

ADT List{

数据对象： $D=\left \{ a_{i} | a_{i}\in Elemset,(i=1,2,...n,n\geq 0) \right \}$

数据关系： $R=\left \{ < a_{i},a_{i-1}> | a_{i},a_{i-1}\in D,(i=1,2,...n) \right \}$

基本操作：InitList(&L)，Destroy(&L)，ListDelete(&L,i,e)等等

}ADT List

4. 线性表的顺序存储运算以及实现

顺序存储的定义：把逻辑上相邻的数据元素存储在物理上也相邻的储存单元中的存储结构。简而言之，逻辑相邻，物理也相邻。

线性表顺序存储结构占用一片连续的存储空间，知道某个元素的存储位置就可以计算其它元素的存储位置，假设线性表的每个元素占据L个储存单元，则第i+1个数据元素的储存位置与第i个数据元素的储存位置之间满足关系：

$LOC(a_{i+1})=LOC(a_{i})+L$

由此，所有的数据元素储存位置均由第一个数据元素的存储位置得到：

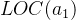
$LOC(a_{i})=LOC(a_{1})+(i-1)\times L$

$LOC(a_{1})$ 为基地址，顺序表中的元素，地址连续，依次存放，随机存取，类型相同，用一维数组来表示正合适。考虑到线性表的运算有插入、删除等，即线性表的表长是可变的。因此，数组的容量应设计的足够大。用data[MAXSIZE]来表示，其MAXSIZE是一个根据实际问题定义的足够大的整数，线性表中的数据从data[0]开始依次顺序存放。但当前线性表中的实际元素个数可能末达到MAXSIZE个，因此，需用一个变量length，记录当前线性表中中最后—个元素在数组中的位置。即起一个指针的作用。由图4.1可看出，需要注意的一点是顺序线性表的逻辑位序与物理位序相差1。

图 4.1 顺序表示意图

4.1 下面以C++模版类给出顺序线性表的定义：

template <class DataType>
class SequenceList
{
public:
	//构造函数、析构函数
	SequenceList();
	~SequenceList() { delete data; };
public:
  //	数据操作部分
	bool InitList();                       //初始化线性表
	void DestroySeqList();                 //销毁线性表
	bool IsEmpty();                        //判断线性表是否空
	bool IsFull();                         //判断线性表是否满
	void TraverseSeqList();                //遍历线性表
	DataType GetTtem(int n);               //获取第n个位置的数据元素的值
	int ListLength();                      //获取顺序表元素个数(线性表长度)
	int LocateItem(DataType i);            //获取与i相同的元素在线性顺序表中的位置
	void InsertItem(int n, DataType i);    //在n处插入数据元素i
	void InsertMultipleItem(int n, int m,DataType i);    //在n处插入m个数据元素i
	void InsertTail(DataType i);           //在顺序表尾部插入数据元素i
	void DeleteItem(int n);                //删除第n个位置的元素
	void SetItem(int n, DataType i);      //将第n个位置的元素改成i
	void DeleteTail();                    //删除尾部位置的元素
	DataType PriorElem(int n);     //若n不是第一个元素，查找第n个元素的前趋
	DataType NextElem(int n);      //若n不是最后一个元素，查找第n个元素的后继
	void ListMerge(SequenceList&L1, SequenceList&L2);   //表合并
public:
	DataType *data;  //指针，存储动态空间申请
	int length;
};

4.2 函数结果状态代码

#define Fault 0
#define True 1
#define Error 0
#define OK 1

4.3 操作算法的实现

4.3.1 初始化线性表

template <class DataType>
bool SequenceList<DataType>::InitList()
{
	this->data = new DataType[MAXSIZE]; //为L申请动态内存空间
		if (!this->data)
		{ //判断是否申请成功
			cout << "申请空间失败！" << endl;
			return Error;
		}
		this->length = 0;
}

首先在堆区开辟空间，然后进行判断，防止内存小分配不成功，如果data为空值，则申请空间操作失败，返回Error。否则，将线性表长度设为0，完成初始化。

4.3.2 销毁线性表

 template<class DataType>
 void SequenceList<DataType>:: DestroySeqList() 
 {
	 this->data = NULL;
	 cout << "顺序线性表线性表已销毁" << endl;
 }

与清空线性表的区别是：销毁线性表后，线性表就不存在了，释放原本的储存空间，但清空线性表之后，线性表仍然存在。

4.3.3 判断线性表是否为空

template <class DataType>
bool SequenceList<DataType>::IsEmpty()
{
	if (this->length == 0)
	{
		return True; 
	}
	else
	{
		return Fault;
	}
}

4.3.4 判断线性表是否为满

template <class DataType>
bool SequenceList<DataType>::IsFull()
{
	if (this->length >= MAXSIZE)
	{
		return True;
	}
	else
	{
		return Fault;
	}
}

4.3.5 遍历线性表

template <class DataType>
void SequenceList<DataType>:: TraverseSeqList()
{
	if (this->length == 0)
	{
		cout << "顺序线性表为空！" << endl;
	}
	if (this->length >= MAXSIZE)
	{
		return;
	}
	for (int i = 0; i < this->length; i++)
	{
		cout << this->data[i] << " ";
	}
	cout << endl;
}

输出线性表中的数据元素。

4.3.6 获取第n个位置的数据元素的值

template <class DataType>
DataType SequenceList<DataType>::GetTtem(int n)
{
	if (n<0 || n>this->length)
	{
		cout << "输入的位置不合法"<<endl;
		return Fault;
	}
	else
	{
		return this->data[n - 1];
	}
}

顺序线性表的逻辑位序与物理位序相差1。i-1的位置存放着第i个数据。

4.3.7 获取顺序表元素个数(线性表长度)

template <class DataType>
int SequenceList<DataType>::ListLength()
{
	if (this->length >=MAXSIZE)
	{
		cout << "顺序线性表已满" << endl;
		return Fault;
	}
	else
	{
		return this->length;
	}
}

4.3.8 获取与i相同的元素在线性顺序表中的位置

顺序表查找算法分析：

查找算法的基本操作为：将记录的关键字同定值进行比较，基本操作：data[j]==i

基本操作执行的次数与要查找的元素和其在表中的位置有关，第1个元素只需要比较1次即可，只需要查找1次，第2个元素查找2次。第n个元素查找n次。

平均查找长度ASL(Average Search Length)

● 为了确定在表中的位置，需要与给定值进行关系比较的关键字的个数的期望值叫做查找算法的平均查找长度。

对含有n个记录的表，查找成功时： $ASL=\sum_{i=1}^{n}P_{i}C_{i}$

$C_{i}$ 找到第i个记录需要比较的次数， $P_{i}$ 第i个记录被查找到的概率。

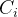
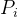
顺序查找的平均查找长度： $ASL=P_{1}+2P_{2}+......+(n-1)P_{n-1}+nP_{n}$

假设每个记录的查找概率相等： $P_{i}=1/n$

则： $ASL_{ss}=\sum_{i=1}^{n}P_{i}C_{i}=\frac{1}{n}\sum_{i=1}^{n}i=\frac{n+1}{2}$

时间复杂度为 $O_{(n)}$

template<class DataType>
int SequenceList<DataType>::LocateItem(DataType i)
 {
	    int currentIndex = -1;
		if (this->length == 0)
		{
			cout << "当前线性表为空" << endl;
			return currentIndex;
		}

		for (int j = 0; j < this->length; j++) {
			if (this->data[j] == i)
			{
				currentIndex = j + 1;
				cout << "数据元素 " << i << " 在当前顺序线性表中第 "<<currentIndex<<" 个位置" << endl;
			}
		}
		if (currentIndex == -1) 
		{
			cout << "数据  " << i<< "  不在当前顺序线性表中" << endl;
		}
		return currentIndex;	
 }

4.3.9 在顺序表尾部插入数据元素i

顺序表插入算法分析：

线性表的插入运算是指在表的 $i(1\leq i\leq n+1)$ 个位置上，插入一个新节点e，使长度为n的线性表，变成长度为n+1的线性表。

算法思想：

① 判断插入位置i是否合法。

② 判断线性表的储存空间是否已经满，若已满则返回Error。

③ 将第n至i位的元素依次向后移动一个位置，空出i的位置。

④ 将要插入的新元素e放入第i个位置。

⑤ 表长+1。

插入算法的时间主要耗费在移动元素的操作上

若插在尾节点之后，则无需移动。

若插在首节点之前，则全部移动。

在各种位置插入（n+1）的平均移动次数:

$E_{ins}=\frac{1}{n+1}\sum_{i=1}^{n+1}(n-i+1)=\frac{1}{n+1}(n+...+1+0)=$ $\frac{1}{n+1}\times \frac{n(n+1)}{2}=\frac{n}{2}$

这说明在顺序表上做插入操作，需要移动表中一半的数据，显然时间复杂度为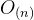 $O_{(n)}$ 。

template <class DataType>
void SequenceList<DataType>::InsertTail(DataType i)
{
	if (!this->data)
	{
		cout << "线性表不存在" << endl;
		return;
	}
	else if (this->length == MAXSIZE)
	{
		cout << "内存已满" << endl;
		return;
	}
	else
	{
		this->data[this->length] = i;
		this->length++;
	}
}

4.3.10 在n处插入数据元素i

template <class DataType>
void SequenceList<DataType>::InsertItem( int n, DataType i)
{
	if (!this->data)
	{
		cout << "线性表不存在" << endl;
		return;
	}
	if ((n < 1) || (n > this->length + 1)) //判定n位置是否合法
	{
		cout << "n位置不合法" << endl;
		return ;
	}
	if (this->length == MAXSIZE)
	{
		cout << "内存已满" << endl;
		return ;
	}
	for (int j = this->length; j>=(n-1); j--)
	{
		this->data[j + 1] = this->data[j];
	
	}
	this->data[n - 1] = i;
	this->length++;
}

4.3.11 在n处插入m个数据元素i

template<class DataType>
void SequenceList<DataType>::InsertMultipleItem(int n, int m, DataType i)
{
	if (!this->data)
	{
		cout << "线性表不存在" << endl;
		return;
	}
	if ((n < 1) || (n > this->length + 1)) //判定n位置是否合法
	{
		cout << "n位置不合法" << endl;
		return;
	}
	if (this->length == MAXSIZE)
	{
		cout << "内存已满" << endl;
		return;
	}
	for (int t = 0; t< m; t++)
	{
		for (int j = this->length; j >= (n - 1); j--)
		{
			this->data[j + 1] = this->data[j];

		}
		this->data[n - 1] = i;
		this->length++;
	}
	if (this->length >= MAXSIZE)
	{
		cout << "插入失败，超过线性表最大容量" << endl;
		return;
	}
}

4.3.12 删除尾部位置的元素

顺序表删除算法分析：

线性表的删除运算是指将表的i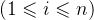 $(1\leqslant i\leqslant n)$ 个位置上的元素去掉，使长度为n+1的线性表，变成长度为n的线性表。

算法思想：

①判断删除位置i是否合法。

②将第i+1至n的元素依次向前移动一个位置。

③表长-1。

与插入运算相同，算法主要时间耗费在元素移动上，平均移动数据元素的次数为

$E_{de}=\sum_{i=1}^{n}P_{i}(n-i)=\frac{1}{n}\sum_{i=1}^{n+1}(n-i)=\frac{n-1}{2}$ 时间复杂度为 $O_{(n)}$ 。

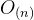
template <class DataType>
void SequenceList<DataType>::DeleteTail()
{
	this->length = this->length - 1;
}

将数据表长度减一，则访问不到最后一个数据元素。

4.3.13 删除第n个位置的元素

void SequenceList<DataType>::DeleteItem(int n)
{
	if (n<0 || n>this->length)
	{
		cout << "要删除的位置不合法";
		return;
	}
	else
	{
		for (int j=n-1;j< this->length;j++)
		{
			this->data[j] = this->data[j + 1];
		}
		this->length--;
	}
}

4.3.14 将第n个位置的元素改成i

 template<class DataType>
 void SequenceList<DataType>::SetItem(int n, DataType i)
{
	 if ((n < 1) || (n > this->length + 1)) //判定n位置是否合法
	 {
		 cout << "n位置不合法" << endl;
		 return;
	 }
	 else
	 {
		 this->data[n - 1] = i;
	 }
}

4.3.15 若n不是第一个元素，查找第n个元素的前趋


template <class DataType>
DataType SequenceList<DataType>::PriorElem(int n)
{
	if (n - 1 == 0)
	{
		cout << "该元素不存在直接前驱" << endl;
		return Error;
	}
	else
	{
		return this->data[n - 2];
	}		
}

4.3.16 若n不是最后一个元素，查找第n个元素的后继

template <class DataType>
DataType SequenceList<DataType> ::NextElem(int n)
{
	if (n - this->length == 0)
	{
		cout << "该元素不存在直接后继" << endl;
		return Error;
	}
	else
	{
		return this->data[n];
	}
}

4.3.17 表合并

template<class DataType>
void SequenceList<DataType>::ListMerge(SequenceList& L1, SequenceList& L2)
{
	this->length = L1.length + L2.length;

	int p1 = L1.length;
	int p2 = L2.length;
	for (int i = 0; i < L1.length; i++) 
	{
		this->data[i] = L1.data[i];
	}
	for (int i = L1.length, j = 0; j < L2.length; j++, i++) 
	{
	this->data[i] = L2.data[j];
	}
	L1.DestroySeqList();
	L2.DestroySeqList();
	cout << "合并完毕！" << endl;
}

第二个for循环中，合并后的表中的数据是从L1.length的长度之后加上去的。

4.3.18 完整代码 SeqList.h头文件与Seqlist.cpp

#pragma once
#include<iostream>
#define MAXSIZE 100
#define Fault 0
#define True 1
#define Error 0
#define OK 1
template <class DataType>
class SequenceList
{
public:
	//构造函数、析构函数
	SequenceList();
	~SequenceList() { delete data; };
public:
  //	数据操作部分
	bool InitList();                       //初始化线性表
	void DestroySeqList();                 //销毁线性表
	bool IsEmpty();                        //判断线性表是否空
	bool IsFull();                         //判断线性表是否满
	void TraverseSeqList();                //遍历线性表
	DataType GetTtem(int n);               //获取第n个位置的数据元素的值
	int ListLength();                      //获取顺序表元素个数(线性表长度)
	int LocateItem(DataType i);            //获取与i相同的元素在线性顺序表中的位置
	void InsertItem(int n, DataType i);    //在n处插入数据元素i
	void InsertMultipleItem(int n, int m,DataType i);    //在n处插入m个数据元素i
	void InsertTail(DataType i);           //在顺序表尾部插入数据元素i
	void DeleteItem(int n);                //删除第n个位置的元素
	void SetItem(int n, DataType i);      //将第n个位置的元素改成i
	void DeleteTail();                    //删除尾部位置的元素
	DataType PriorElem(int n);     //若n不是第一个元素，查找第n个元素的前趋
	DataType NextElem(int n);      //若n不是最后一个元素，查找第n个元素的后继
	void ListMerge(SequenceList&L1, SequenceList&L2);   //表合并
public:
	DataType *data;  //指针，存储动态空间申请
	int length;
};

#include<string>
#include"SeqList.h"
using namespace std;
template <class DataType>
SequenceList<DataType>::SequenceList()
{
	this->data = new DataType[MAXSIZE];
	this->length = 0;
}
template <class DataType>
bool SequenceList<DataType>::InitList()
{
	this->data = new DataType[MAXSIZE]; //为L申请动态内存空间
		if (!this->data)
		{ //判断是否申请成功
			cout << "申请空间失败！" << endl;
			return Error;
		}
		this->length = 0;
}
template <class DataType>
bool SequenceList<DataType>::IsEmpty()
{
	if (this->length == 0)
	{
		return True; 
	}
	else
	{
		return Fault;
	}
}
template <class DataType>
bool SequenceList<DataType>::IsFull()
{
	if (this->length >= MAXSIZE)
	{
		return True;
	}
	else
	{
		return Fault;
	}
}
template <class DataType>
void SequenceList<DataType>::InsertItem( int n, DataType i)
{
	if (!this->data)
	{
		cout << "线性表不存在" << endl;
		return;
	}
	if ((n < 1) || (n > this->length + 1)) //判定n位置是否合法
	{
		cout << "n位置不合法" << endl;
		return ;
	}
	if (this->length == MAXSIZE)
	{
		cout << "内存已满" << endl;
		return ;
	}
	for (int j = this->length; j>=(n-1); j--)
	{
		this->data[j + 1] = this->data[j];
	
	}
	this->data[n - 1] = i;
	this->length++;
}
template <class DataType>
void SequenceList<DataType>::InsertTail(DataType i)
{
	if (!this->data)
	{
		cout << "线性表不存在" << endl;
		return;
	}
	else if (this->length == MAXSIZE)
	{
		cout << "内存已满" << endl;
		return;
	}
	else
	{
		this->data[this->length] = i;
		this->length++;
	}
}	
template<class DataType>
void SequenceList<DataType>::InsertMultipleItem(int n, int m, DataType i)
{
	if (!this->data)
	{
		cout << "线性表不存在" << endl;
		return;
	}
	if ((n < 1) || (n > this->length + 1)) //判定n位置是否合法
	{
		cout << "n位置不合法" << endl;
		return;
	}
	if (this->length == MAXSIZE)
	{
		cout << "内存已满" << endl;
		return;
	}
	for (int t = 0; t< m; t++)
	{
		for (int j = this->length; j >= (n - 1); j--)
		{
			this->data[j + 1] = this->data[j];

		}
		this->data[n - 1] = i;
		this->length++;
	}
	if (this->length >= MAXSIZE)
	{
		cout << "插入失败，超过线性表最大容量" << endl;
		return;
	}
}
template <class DataType>
void SequenceList<DataType>:: TraverseSeqList()
{
	if (this->length == 0)
	{
		cout << "顺序线性表为空！" << endl;
	}
	if (this->length >= MAXSIZE)
	{
		return;
	}
	for (int i = 0; i < this->length; i++)
	{
		cout << this->data[i] << " ";
	}
	cout << endl;
}
template <class DataType>
int SequenceList<DataType>::ListLength()
{
	if (this->length >=MAXSIZE)
	{
		cout << "顺序线性表已满" << endl;
		return Fault;
	}
	else
	{
		return this->length;
	}
}
template <class DataType>
void SequenceList<DataType>::DeleteItem(int n)
{
	if (n<0 || n>this->length)
	{
		cout << "要删除的位置不合法";
		return;
	}
	else
	{
		for (int j=n-1;j< this->length;j++)
		{
			this->data[j] = this->data[j + 1];
		}
		this->length--;
	}
}
template <class DataType>
void SequenceList<DataType>::DeleteTail()
{
	this->length = this->length - 1;
}
template <class DataType>
DataType SequenceList<DataType>::GetTtem(int n)
{
	if (n<0 || n>this->length)
	{
		cout << "输入的位置不合法"<<endl;
		return Fault;
	}
	else
	{
		return this->data[n - 1];
	}
}
template <class DataType>
DataType SequenceList<DataType>::PriorElem(int n)
{
	if (n - 1 == 0)
	{
		cout << "该元素不存在直接前驱" << endl;
		return Error;
	}
	else
	{
		return this->data[n - 2];
	}		
}
template <class DataType>
DataType SequenceList<DataType> ::NextElem(int n)
{
	if (n - this->length == 0)
	{
		cout << "该元素不存在直接后继" << endl;
		return Error;
	}
	else
	{
		return this->data[n];
	}
}
 template<class DataType>
 void SequenceList<DataType>::SetItem(int n, DataType i)
{
	 if ((n < 1) || (n > this->length + 1)) //判定n位置是否合法
	 {
		 cout << "n位置不合法" << endl;
		 return;
	 }
	 else
	 {
		 this->data[n - 1] = i;
	 }
}
 template<class DataType>
 void SequenceList<DataType>:: DestroySeqList() 
 {
	 this->data = NULL;
	 cout << "顺序线性表线性表已销毁" << endl;
 }
 template<class DataType>
int SequenceList<DataType>::LocateItem(DataType i)
 {
	    int currentIndex = -1;
		if (this->length == 0)
		{
			cout << "当前线性表为空" << endl;
			return currentIndex;
		}

		for (int j = 0; j < this->length; j++) {
			if (this->data[j] == i)
			{
				currentIndex = j + 1;
				cout << "数据元素 " << i << " 在当前顺序线性表中第 "<<currentIndex<<" 个位置" << endl;
			}
		}
		if (currentIndex == -1) 
		{
			cout << "数据  " << i<< "  不在当前顺序线性表中" << endl;
		}
		return currentIndex;	
 }
template<class DataType>
void SequenceList<DataType>::ListMerge(SequenceList& L1, SequenceList& L2)
{
	this->length = L1.length + L2.length;

	int p1 = L1.length;
	int p2 = L2.length;
	for (int i = 0; i < L1.length; i++) 
	{
		this->data[i] = L1.data[i];
	}
	for (int i = L1.length, j = 0; j < L2.length; j++, i++) 
	{
	this->data[i] = L2.data[j];
	}
	L1.DestroySeqList();
	L2.DestroySeqList();
	cout << "合并完毕！" << endl;
}

int main()
{ 
	SequenceList<int>L1;
	SequenceList<int>L2;
	SequenceList<int>L3;
	L1.InsertTail(1);
	L1.InsertTail(2);
	L1.InsertTail(3);
	L1.InsertTail(4);
	L1.TraverseSeqList();

	L2.InsertTail(4);
	L2.InsertTail(3);
	L2.InsertTail(2);
	L2.InsertTail(1);
	L2.TraverseSeqList();

	L3.ListMerge(L1, L2);
	L3.TraverseSeqList();
	system("pause");
	return EXIT_SUCCESS;
}

5. 顺序储存结构的优缺点

优点：

● 储存密度大，结点本身所占储存量/结点结构所占储存量，
● 可以随机存取表中任一元素，
缺点：

● 插入，删除某一个元素时，需要移动大量元素，
● 浪费储存空间
● 属于静态储存形式，数据元素的个数不能自由扩充，最大能放置的元素个数已经被固定，当表中元素变化大的时候，就显得不够灵活。
为了克服这些缺点，使用另一种储存方式————>链式储存结构。

下一篇——————————