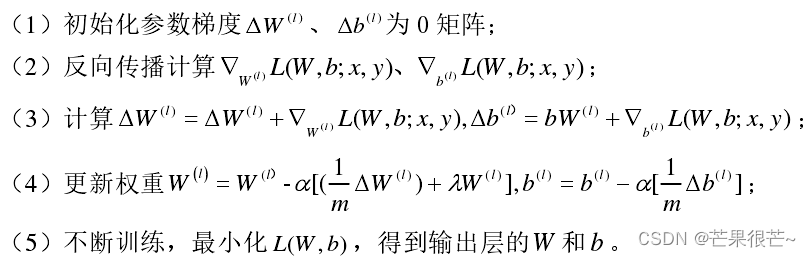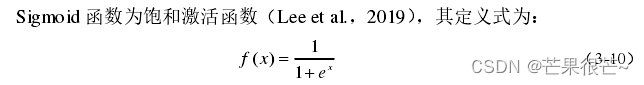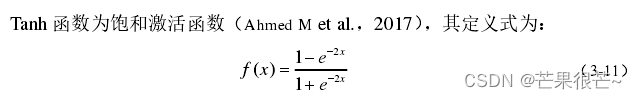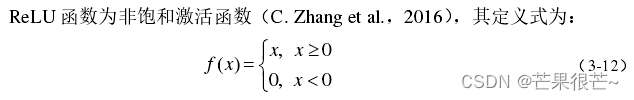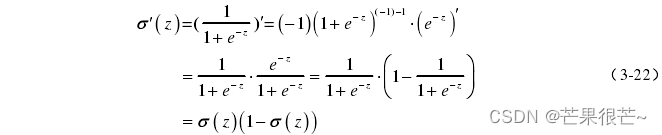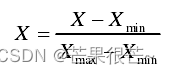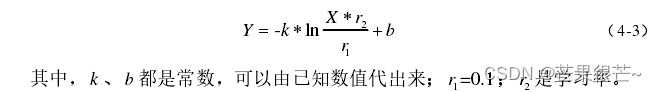一、简介
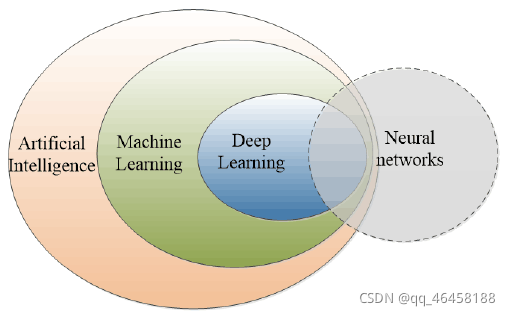
深度学习是包含多个隐层的机器学习模型,核心是基于训练的方式,从海量数据中挖掘有用信息,实现分类与预测。
早期的深度学习模型:编码器、循环神经网络、深度置信网络、卷积神经网络
衍生模型:堆叠降噪自编码器、稀疏自编码器、降噪自编码器
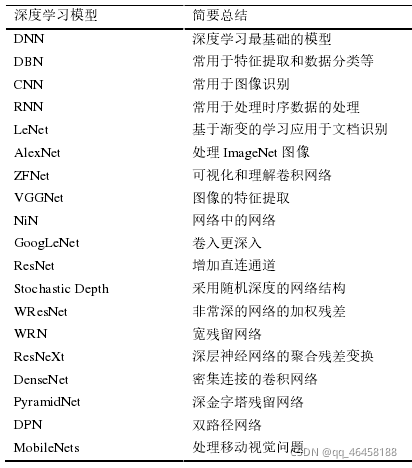
深度学习的常用模型:卷积神经网络(CNN),深度信念网络(DBN),深度自动编码器(DAE),限制玻尔兹曼机(RBM)。CNN有全监督学习和权值共享的特点,在自然语言处理和语音图像识别领域有很强优势。其他深度学习模型大多先采用无监督方式逐层预训练,再使用有监督方式调整参数。共同之处:采取分层的结构来处理问题的思想。模型的基本元件为神经元,具有多层次结构,训练方式为梯度下降,训练过程可能出现过拟合或欠拟合的情况。
深度神经网络模型(Deep netural network,DNN)是深度学习的基础模型之一,较于浅层机器学习,DNN具有更深的层次结构,拥有更好的语音识别、图像处理(百度识图,人脸识别)、自然语言处理(基于笔法匹配识别手写文字)。
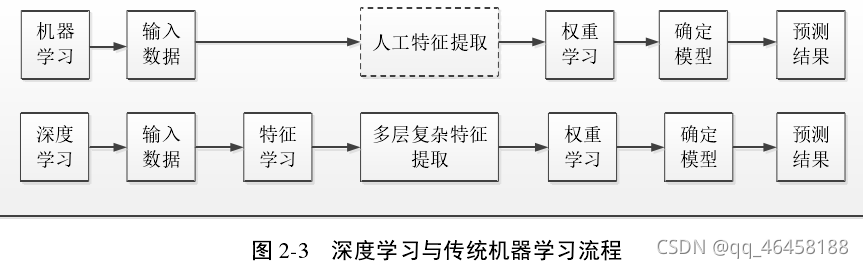
深度学习的效果优于传统的多层神经网络,最大的改进:深度学习算法结合了无监督特征学习与有监督特征学习,将多层结构中的上层输出作为下层输入,经过层与层之间的非线性组合。
二、流程
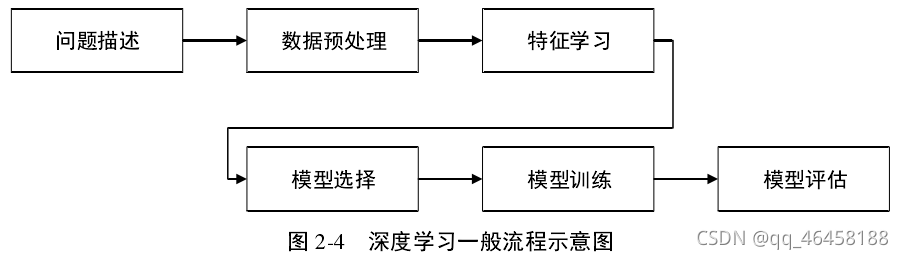
a.问题描述:将具体问题解译为深度学习能求解的问题。
b.数据预处理:因数据量较大,易出现误差,据具体模型和任务要求,对数据进行预处理。
c.特征学习:数据的复杂性和变化性,为了从原始数据中挖掘有用特征,借助机器来学习和提取特征。
d.模型选择:数据特征的差异性,选择合适的深度学习模型,对模型优化、损失函数、激活函数、输入输出变量等。
e.模型训练:面向实际任务,选择最优的建模方法和参数。方式:选择多种算法进行运行,比较运行结果,在最优模型基础上进行参数调整。
f.模型评估:建立合适的评价指标。
三、基础知识
目前,深度学习常用模型主要有:卷积神经网络 CNN,深度信念网络 DBN,深度自动编码器 DAE,限制玻尔兹曼机 RBM 等。
卷积神经网络具有全监督学习和权值共享的特点,在自然语言处理和语音图像识别领域拥有很强的优势。其它的深度学习模型,大多都采用先进行无监督方式的逐层预训练,然后再使用有监督方式的调整参数。
虽然其结构参数、训练方式、模型泛化能力以及面向的对象各不相同,但是其基本思想和模块相同。所有深度学习模型的共同之处:采用分层的结构来处理问题;神经元是模型中的基本元件,模型具有多层次结构,各层都由神经元构成,模型的训练都是通过梯度下降方式,训练过程中可能会出现过拟合或者欠拟合的情况等。
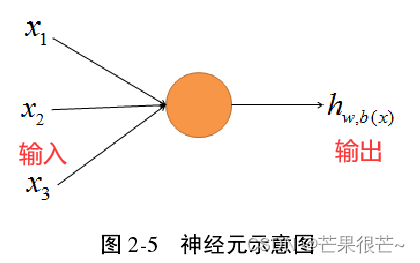
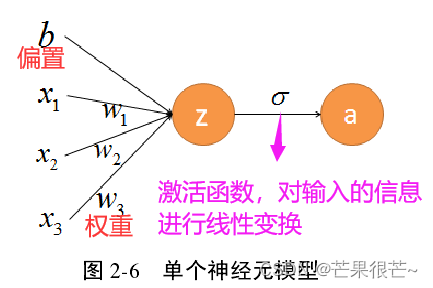
1.神经元
神经网络结构的基础单元,受生物神经元的启迪,作用是接收信号并得到输出。神经网络的每一层含一个或数个神经元。
任意神经元的输出 是 网络结构中另外神经元的输入 ,因此神经元接收信号的个数将由前一层限定,且接收到的不同信号对该神经元的刺激程度不同。 神经元的输出为全部输入信息在线性作用下的和,用 a 表示。
当模型中神经元个数唯一的时候——感知机模型。感知机能够快速收敛。但由于单个神经元的模型其线性拟合程度不高,导致感知机的学习能力差,不能处理非线性问题。层次结构的深度学习模型在感知机的基础上衍生而来。
2.感知机和梯度下降
用某个误差函数来表示输出值与真实值的偏差,对模型进行训练的目的在于让误差取到最小值。函数导数为0可取极值,且只有当其导函数在下降的过程中才能取得极小值。为了求出 E 的极小值点,通常沿着函数负梯度方向进行迭代,如果可以取一个确切的步长,就可以使函数收敛到局部极小点。
梯度下降的原理就是通过负梯度的训练方式,得到一组W 、b ,使误差函数取最小值。
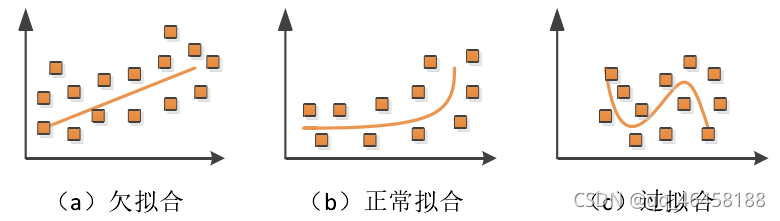
3.过拟合和欠拟合
过拟合:深度学习模型在训练集数据上进行训练时,表现出了极好的能力,能够对训练集数据完全拟合,但是当测试集数据用于训练好的模型时,模型表现出极差的泛化能力,甚至完全达不到模型的预期效果。 深度神经网络结构复杂,其模型的参数和变量极多,在模型训练时需更多的数据作为支撑。过少的训练集数据或者过长的训练时间,可能导致过拟合。
防止过拟合的方法:
a.early stopping:在模型训练准确率停止增加时中断模型的运行,防止因训练时间过长造成过拟合。要动态分析模型的运行。
b.数据增强(data augmentation):通过继续对研究区调研扩充数据;或在已有数据的基础上,扩大基础数据集规模,常用的数据增强的方式有加入“噪声”数据、对图像进行锐化、裁剪等。
c.正则化(Regularization) :在模型中增加惩罚项,使多参数下的模型能够受到更小的影响,进而防止模型过度训练。
d.Dropout :随机“舍弃”神经网络结构中的部分神经元。使模型在训练时,网络结构发生了变化,即神经元的组合方式改变了。
欠拟合:模型拟合的曲线与数据偏离较大,拟合程度低。通过再训练或选择使用别的深度学习模型进行处理。
4.深度学习常用模型介绍
5. epoch\batchsize\迭代次数
epoch:所有训练数据集都训练过一次,“一代训练”,即用训练集的全部数据对模型进行一次完整的训练。
batchsize:在训练集中选一组样本用来更新权值,“一批数据”,
iteration:使用一个Batch数据对模型进行一次参数更新的过程,“一次训练”。训练时,1个batch训练图像通过网络训练一次(一次前向传播+一次后向传播),每迭代一次权重更新一次;测试时,1个batch测试图像通过网络一次(一次前向传播)。所谓iterations就是完成一次epoch所需的batch个数。
一次迭代如果把数据集中的数据都跑一遍,速度会很慢,所以一次iteration只使用部分数据,这个数目就称为batch_size,1个batch所包含的样本数目通常设为2的n次幂,常用的包括64,128,256。 网络较小时选用256,较大时选用64。epoch这个概念,指所有数据都被过一次了。
四、深度神经网络(DNN)
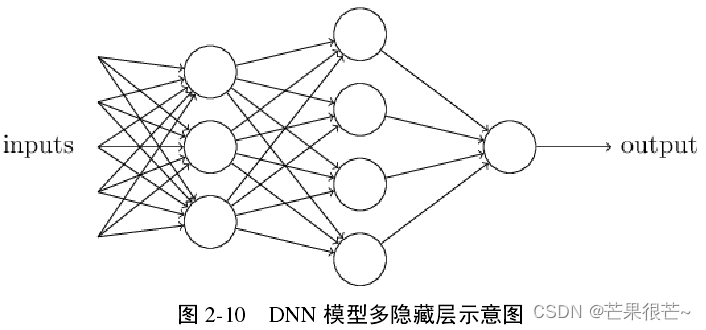
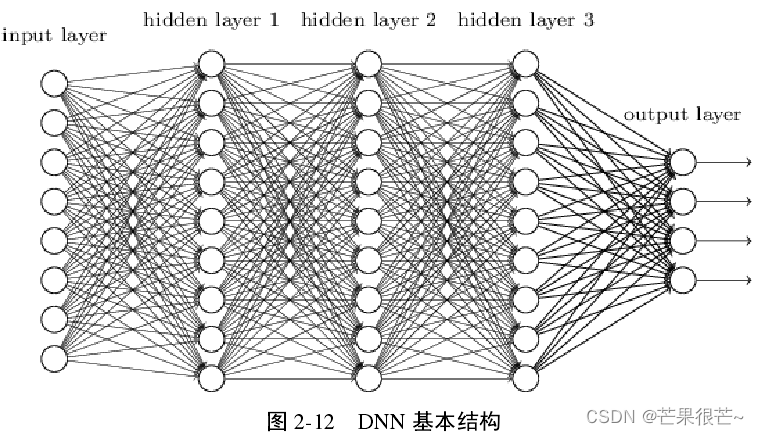
感知机模型仅含单个神经元,含有多层神经元结构的模型——多层感知机。深度神经网络属于多层感知机的范畴,其特点包括:
a.多隐藏层:更深层次的 DNN 模型,处理问题的能力得到加强,但随着隐藏层层数的增多,模型也更加复杂。
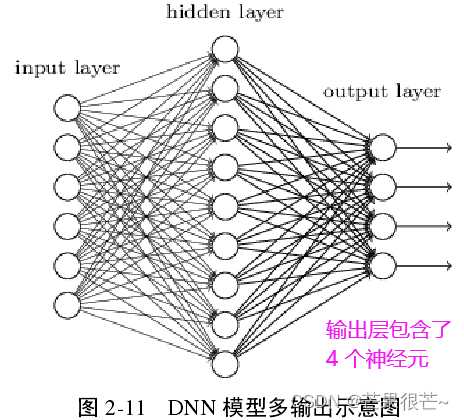
b.灵活的模型输出:较于感知机的单个输出,DNN 模型的输出可以大于1,也就是说模型能够适用于更多领域了。
c.多选择性的激活函数:感知机模型仅将 sign(z) 作为激活函数,处理复杂问题时有其局限性。DNN 模型中,随着网络结构的扩张,可选择的激活函数更多样,处理问题的能力也得到了提高。
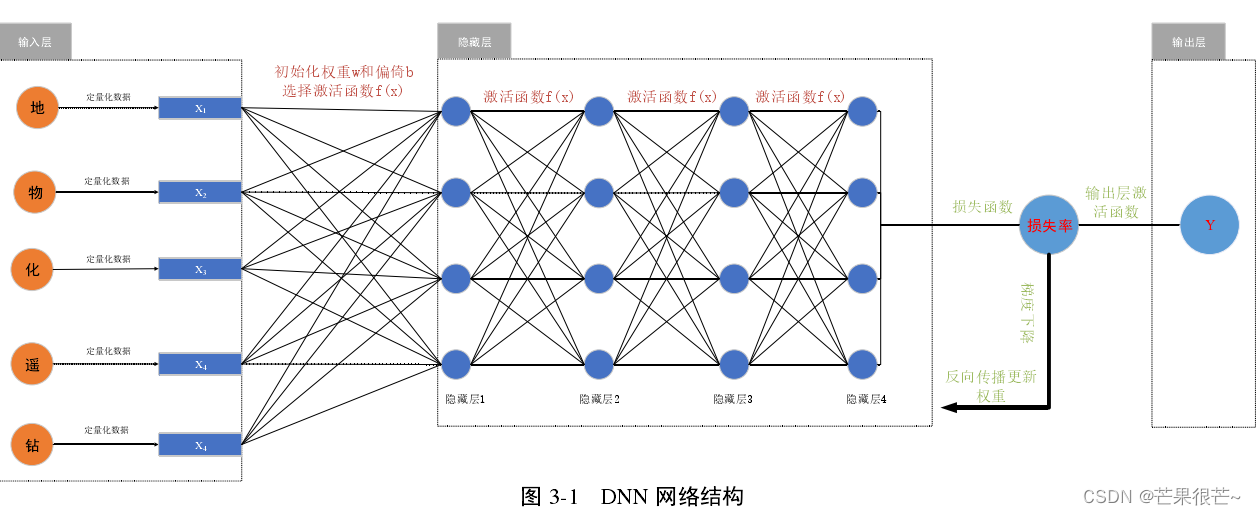
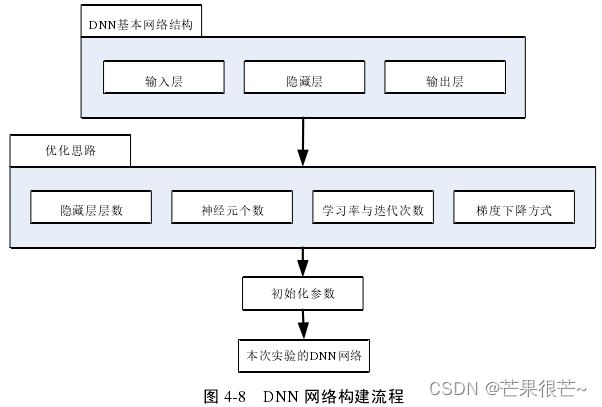
1.DNN的基本结构
DNN 模型是经典三层架构,并且各层的神经元与邻层的神经元连接。
输入层用于接收原始输入信息;
隐藏层通过激活函数的处理,将信息传入下一层;
输出层用于整合所有隐藏层的运算,并输出模型的最终结果。
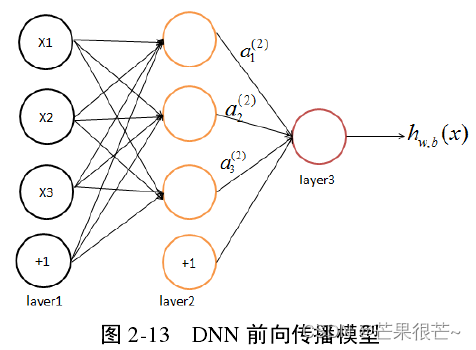
2.DNN前向传播算法
DNN 前向传播原理:通过对输入 x 进行运算,最终得到输出 y 。输入是图像、语音、文本或地质数据等,采用逐层训练的方式,得到 DNN模型的输出。
3.DNN反向传播算法
通过正向传播计算得到实际值与预测值的误差,将误差通过输出层返回到隐含层,再从隐含层传递到输入层,在反向传播的过程中,通过不断更新权值使得预测值与实际值之间的误差减小,直至达到所设定的误差阈值时才结束训练。步骤为:
五、深度学习常用框架
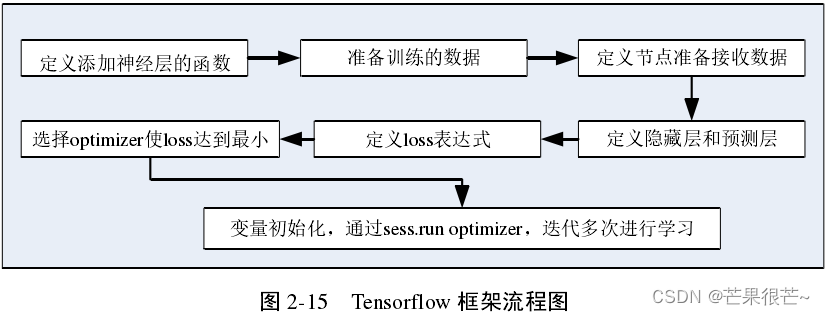
1.Tensorflow
起源于谷歌的 DistBelief 算法库,作为实现深度学习算法的基本框架,以其多层次的结构,受到了各个领域研究人员的青睐。由于 Tensorflow 性能稳定、结构灵活,同时其代码开源,因此它一出现就成为了深度学习中最常用的框架。
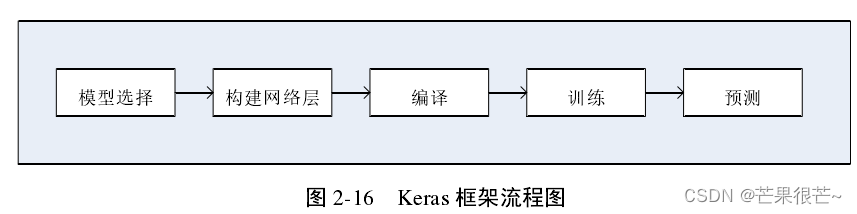
2.Keras
以 Python 为基本编程语言,基于面向对象的方式设计代码。因其具有灵活的运行机制,支持 DNN、CNN 和 RNN 以及几者的组合,且基于 TensoFlow、CNTK 和 Theano 后端,在深度学习算法实现中也备受关注。
3.其他
六、基于 DNN 的多源信息预测模型构建
1.DNN网络结构设计
输入层到中间层的第一层对权重和偏置进行了初始化;通过梯度下降方式更新参数;最终输出深部成矿预测概率值。
输入层:输入原始数据 。
隐藏层:提取特征。隐藏层对网络结构外部的信息不能直接接受或发放,通过层间全连接的方式,对数据中的特征信息进行融合,多隐藏层的加入,有利于 DNN 模型对于非线性问题的解决。
输出层:输出 DNN 算法对原始输入信息的预测结果。DNN 模型通过学习的方式得到了最佳参数,此时的模型近于完美。再将测试集应用于模型时,便能得到最终的预测结果,该结果通过输出层来表征。
2.DNN网络参数设置
在 DNN 模型构建过程中,首要任务是确定隐藏层层数以及各层神经元个数。隐藏层层数和神经元个数太少,模型效果欠佳;太多,网络性能变差,易陷入局部最小,降低模型训练速度。模型中的权值和阈值数随隐藏层层数和神经元个数的变化而变化。
输入节点数应为研究区的地质变量数,输出层节点数为 1(期望模型的最终输出为成矿概率值)。
(1)隐藏层层数
多隐藏层的条件下,网络训练精度更高,但是随着模型层次的深入,模型训练需更多的时间,甚至“过拟合”。
隐藏层层数也就是“深度学习”的“深度”。DNN 模型预测的准确度与隐藏层层数之间不存在线性关系,这也就意味着,在模型深度逐渐增加的过程中,会出现一个拐点,使得模型效果随着深度的增加而降低。
有人提出DNN 的隐藏层层数与输入、输出的神经元个数有关,但是至今仍未出现一种通用模式。目前常用的方式是进行试错实验,在 1 个隐藏层的基础上逐步增加,通过模型训练效果以及收敛速度进行评估,以确定最合适的隐藏层层数。
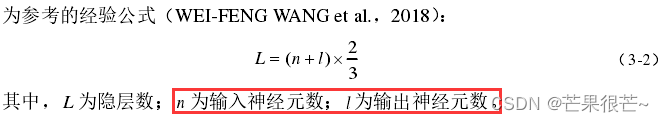
(2)神经元个数
从公式(3-1)可以看出,隐藏层神经元个数作为被乘数,其微小的变化都会引起权值和阈值的总数产生较大变化。
3.激活函数的选择
在加入激活函数前,神经元通常对输入数据产生线性反馈,但是这样就难以解决复杂的非线性问题。激活函数的作用是给 DNN 模型添加非线性手段,能够有效提升模型的实际能力。激活函数可以分为饱和、硬饱和与软饱和。

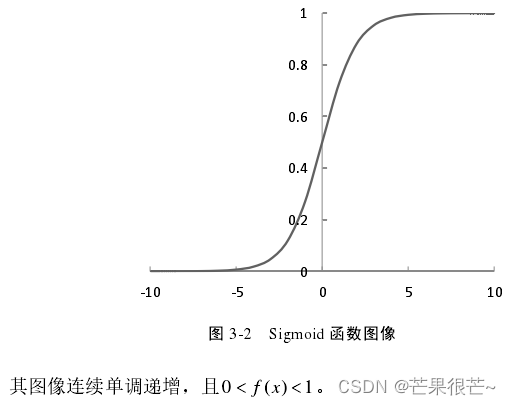
(1)Sigmoid函数
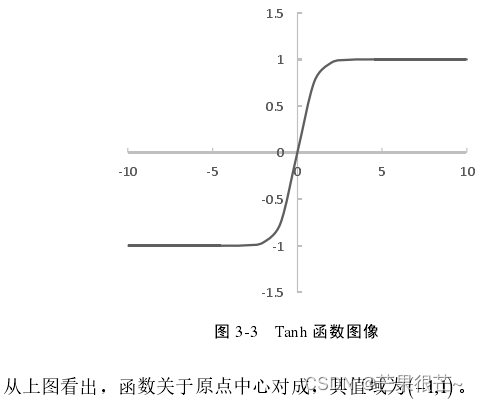
(2)Tanh函数
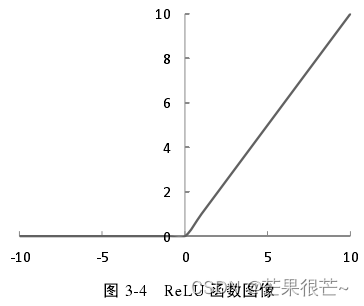
(3)ReLU函数
(4)Leaky Re LU函数
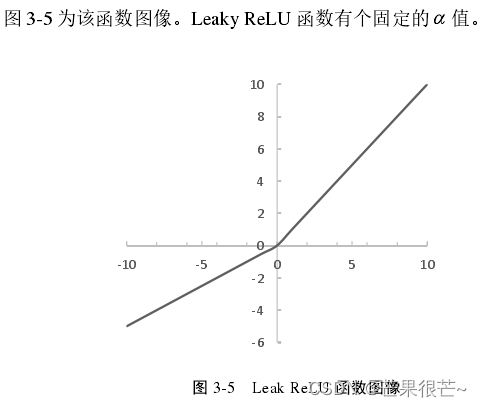
4.输出层激活函数与损失函数
DNN 模型效果的好坏及收敛的快慢都与输出层有很大的关系,故要合理选择输出层激活函数与损失函数。
本文主要研究的问题是多源信息下的深部矿产资源预测,因此我们期望模型最终输出结果为 0-1 之间的数值,即表示为最终的预测概率,本文模型输出层采用 Sigmoid 激活函数函数,而损失函数可以选择均方差或交叉熵。
(1)均方差损失函数

在模型反向传播更新权重的时候,总是乘了,当神经元的输入 z 远离 0 时,模型的W 、b 更新缓慢,即算法收敛很慢。 采用均方差损失函数时,模型收敛较慢。
(2)交叉熵损失函数
从公式(3-20)、(3-21)可以看出,W 、b 的梯度更新与无关,而是与
成正比关系,即模型输出的误差越大,则W 、b 更新越快,这也就意味着模型能够迅速收敛。因此,本文模型在输出层使用交叉熵损失函数。
七、DNN模型的应用
1.研究区简介
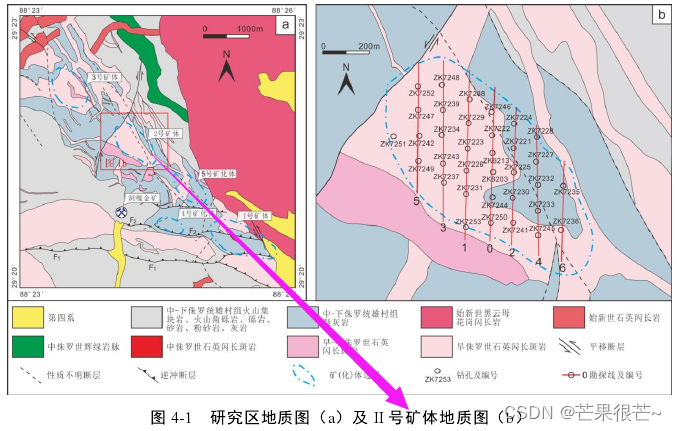
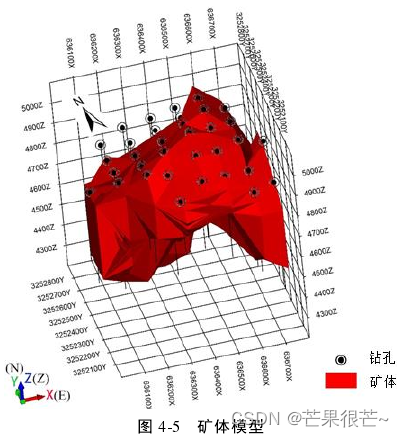
研究区的找矿潜力巨大,除 I 号矿体勘查程度较高已进入矿山开发阶段外,I 号矿体外围的 II、III、IV 和 V 号矿体等深部、边部均未控制,Ⅱ号矿体勘探区之间,物化探显示找矿潜力极大,存在具有勘查潜力的重要化探异常带。在 II 矿体范围内,目前已实施 34 个钻孔,钻孔揭示在该矿体的深部(800m 以下)和边部(北西侧和南东侧)均未完全控制,尤其以深部显示出巨大找矿潜力。研究区地质图与 II 号矿体地质图。 基于 DNN 的多源信息预测模型应用于该研究区。
2.环境搭建
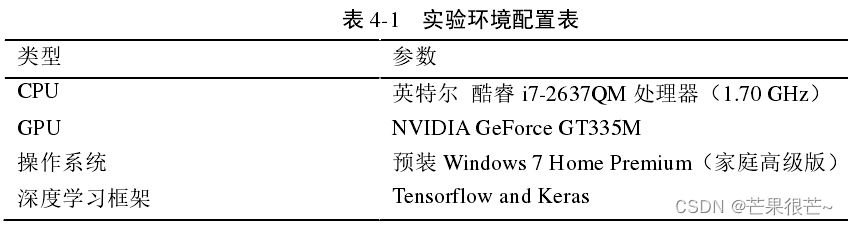
模型应用的基础条件:计算机的运行环境配置,主要包括 CPU、GPU、操作系统、深度学习框架的选择。
3.三维地质体模型构建及多源信息提取
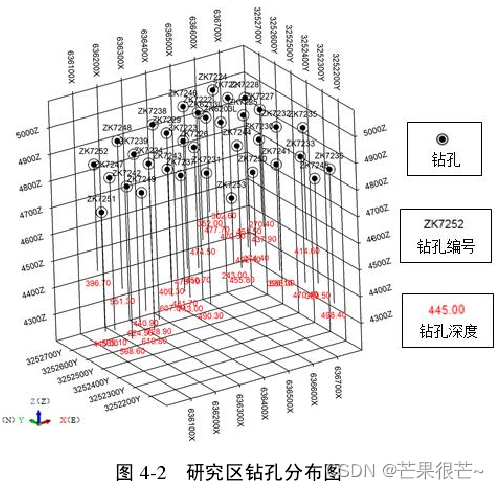
实验数据:来源于研究区已有成果资料,主要包括了钻孔、剖面等成果数据。在研究区共设计了 8 条勘探线,共 34 个钻孔,对每个钻孔的 Au、Ag、Cu 三种化分元素进行了分析,研究区钻孔分布图。
(1)岩性的整数编码
在 DNN 模型中,必须保证其输入和输出变量都为具体数值。岩性作为分类数据,不能直接被定义为模型的输入变量,需要将岩性编码为数字。 本文采用整数编码技术,将岩性映射到整数上。

(2)数据归一化
研究区原始数据样本具有较明显的量级差别,为了消除数量级的不同对网络模型的训练及测试的影响,使网络更快收敛,对原始数据进行归一化。
(3)三维地质体模型构建
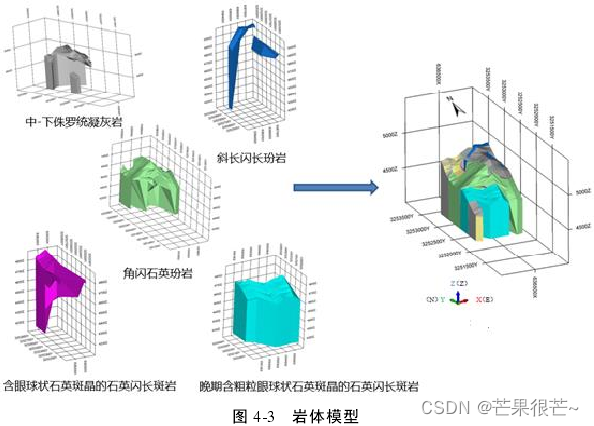
三维可视化技术,是利用计算机来实现数据的可视化表达。以处理后的数据作为基础,借助三维可视化技术,分别构建了矿
区的岩体、围岩蚀变、矿体以及 Au、Ag、Cu 三种化分元素的实体模型。
岩体模型:以矿区岩性数据为基础,构建矿区的岩体模型。((1)中的岩性整数编码)
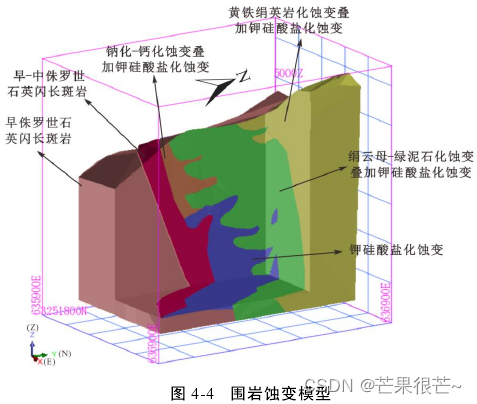
围岩蚀变模型:通过对Ⅱ号矿体钻孔岩芯的详细编录,总结其蚀变分带特征,构建其围岩蚀变模型。
矿体模型:矿体在空间上呈不规则椭球体,主要为原生硫化物矿体,在勘查区内,矿体主要位于海拔 4211m 至 5050m 之间,最大见矿深度 728.9m(海拔4211.58m)。
化分元素实体模型:钻孔岩芯中 Au、Ag、Cu 三种元素,根据元素含量数据进行三维可视化建模.
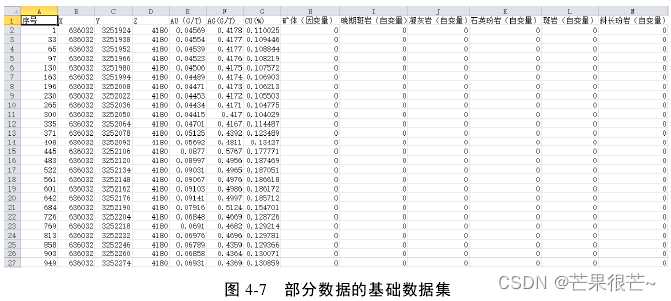
基于已建立的各种三维地质体模型,按照8*14*12的尺度划分小立方体,形成块体模型;然后采用克里格插值法对块体模型进行赋值,得到基础数据集,为后续模型训练集与测试集的制备奠定了基础。
4.基于DNN的成矿预测网络结构核心参数确定
在 DNN 基本结构的基础上对模型进行优化。根据优化后的结果,初始化网络结构参数,得到本实验DNN 网络结构。
(1)隐藏层层数
隐藏层层数也就是“深度学习”的“深度”。DNN 模型预测的准确度与隐藏层层数之间不存在线性关系,在模型深度逐渐增加的过程中,会出现拐点,使得模型效果随着深度的增加而降低。
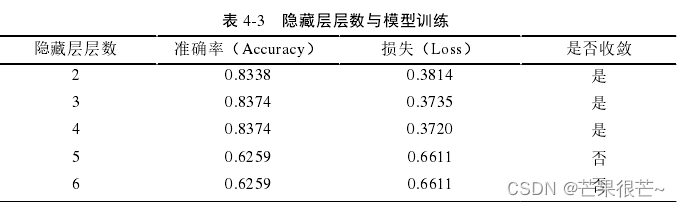
根据公式(3-2)计算出理论上最优的隐藏层层数为 4 。为判断其对模型应用的影响,先固定其它外部参数统一不变,仅将隐藏层层数作为变量,表 4-3 是迭代次数为 200 时,模型训练的准确率、损失以及收敛性的情况。 本实验将隐藏层层数设定为4 层。
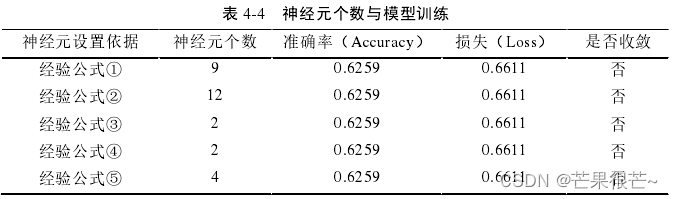
(2)神经元个数
保持其他参数不变,隐藏层层数固定为 4 层时,利用上一章提到的 5 个经验公式分别设置神经元个数,得出在不同神经元个数的条件下,模型训练的准确率、损失以及收敛性的情况。
?根据经验公式可算出神经元个数,但准确率、损失、是否收敛是如何得知
模型训练的准确率较低、损失极高、模型难以收敛——经验公式无法计算出本文模型应用的最优神经元参数。 几种情况下模型训练的准确率和损失值都相同(0.6259 和 0.6611)——表明模型的泛化能力差,存在欠拟合的现象。
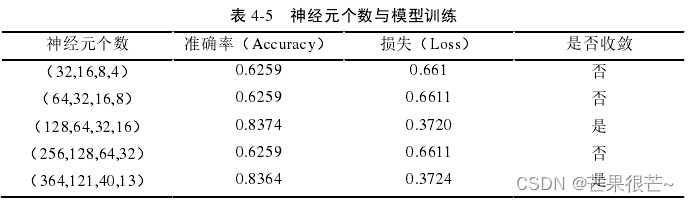
措施:先基于计算机二进制的运算方式,将神经元个数设为 2n;其次,本文研究的问题为多个输入变量经过深度学习模型的训练后,最终得到一个输出变量,其隐藏层神经元数量应服从先递增后递减的规律。 为了加强模型泛化能力,适当增加模型训练时间,并进行大量重复实验,最终得到了表 4-5 所示结果。 本文最终将隐藏层神经元个数设置为(128,64,32,16)。
隐藏层神经元数量应服从先递增后递减的规律,但表格中神经元个数为单调递增/递减的
(3)学习率与迭代次数
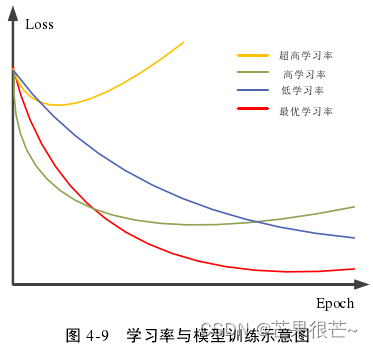
学习率:DNN 的主要参数之一,学习率与模型训练的示意图。
较高学习率:模型训练前期损失下降较快,但后期最终损失大大高于最优学习率的效果;无论我们选择的学习率是高于/低于最优学习率,模型训练的损失都有不同程度的增大,尤其是超高学习率的情况下,模型甚至无法收敛;本文在对模型进行实际应用时,借助了一种自适应学习率的Adam 算法,来对学习率这一参数进行了优化,其算法流程为上图。
迭代次数:用 Tensorflow 设计 DNN 模型需要固定一个迭代次数 ,迭代多次进行学习。
从公式(4-3)可以看出,迭代次数 X 对 DNN 模型的输出Y 影响巨大,所以迭代次数应该是模型性能的一个决定性因素。由于深度神经网络的复杂性,在实际实验中,通常根据模型效果确定迭代次数。
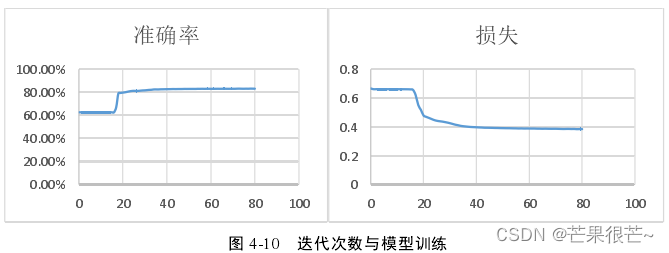
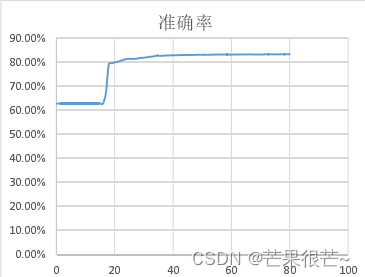
本实验在固定隐藏层层数为 4 层、神经元个数为(128,64,32,16)、采用Adam 自适应算法优化学习率的基础上,得出了准确率和损失曲线。从而确定迭代次数。迭代次数在 80 左右模型表现出良好的收敛性,准确率较高、损失较小。迭代次数设定为 80 次。
(4)梯度下降方式
常用的梯度下降方法及优缺点。本文选用了兼备速度和准确度的小批量梯度下降法(MBGD)。Batch 取值视具体情况而定,尽可能取 2的次数,因为计算机存储是 2 进制的,在计算机运行时会有一定的优化。
(5)本次实验的模型参数配置
5.模型评价指标
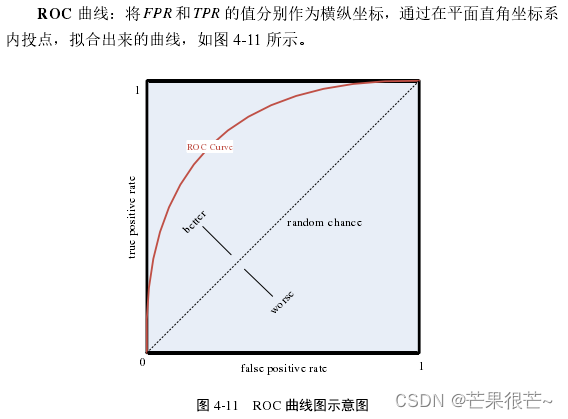
正确率、查准率、召回率、F 值、ROC 曲线几个方面对模型进行评价 。
查准率和召回率的区别:查准率是基于预测的结果,预测有矿中真的有矿/真的没矿的比例; 召回率是基于现实的实际情况,真的有矿中预测有矿的比例、真的没矿中预测有矿的比例。
ROC 曲线的图像通常在 y=x 左上方,曲线上凸的弧度越大模型预测的效果越好。曲线下方与坐标轴组成的区域面积为 AUC,用来表征模型预测的准确性,AUC < =0.5 时,模型无实际意义;0.5<AUC <0.9时,模型准确性一般;AUC >0.9时,模型准确性高。曲线上与 (0,1) 点距离最近的点对应的阈值是最好的。
6.预测结果及分析
(1)模型训练集与测试集
在三维地质体模型的基础上,以深度作为划分依据,将地表到地下 540m 作为训练集,540m以深作为测试集。
(2)模型训练效果分析
按照前文所述的初始化参数配置,首先用训练集数据对模型进行训练,得到模型训练准确率以及损失。
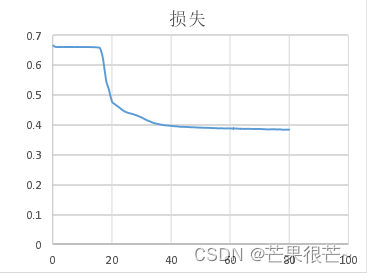
在迭代次数为 30 次左右,模型训练的准确率和损失曲线趋于平稳,说明模型具有较好的收敛性; 模型训练达到收敛时,准确率为 83%左右,损失约为 0.38,说明本文构建的 DNN 模型性能较好。
(3)模型预测结果分析
模型训练完成后,将测试集数据用于优化后的 DNN 模型,得到最终输出值,通过制作模型预测输出的数据表,绘制 ROC 曲线,以 AUC 来评估预测结果与研究区实际情况的吻合程度。
ROC 曲线上拱较高,AUC 的值=0.932,表明本文构建的基于DNN 的多源信息预测模型质量较好;当阈值取 0.85 时,模型预测的准确率、查准率、召回率、F值分别为:87.26%、80.21%、70.32%,74.94%,进一步说明了基于 DNN 的模型效果较好。
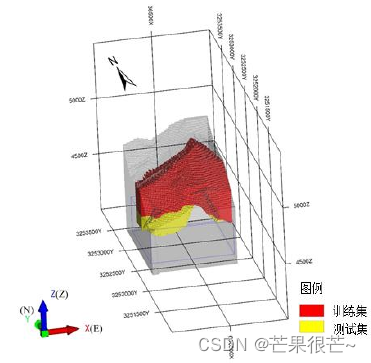
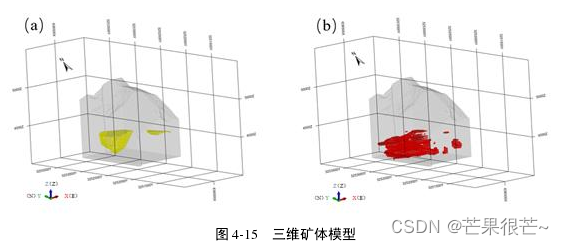
预测值中>= 0.85 的值定义为预测成矿点,得到基于 DNN 预测的三维矿体模型(b),与研究区的实际矿体模型(a)进行对比。
比较三维矿体模型:预测结果与矿区实际情况在成矿位置和规模上较吻合——DNN 算法可有效挖掘矿体分布的空间位置关系。
优化后的 DNN 模型:在训练过程中表现出高准确率、低损失以及良好的收敛性;从 DNN 的预测评价指标来看,各个指标的得分都较高——表明本文构建的基于 DNN 的多源信息预测模型,能够提取到地质大数据中更充分的有用信息,从而达到了良好的预测效果,进一步证明了深度学习方法在深部成矿预测中的可行性。
首先搭建实验的软硬件平台——对收集到的原始数据进行了预处理,并建立了数据的三维可视化模型——将处理后的基础数据集划分成训练集与测试集——从隐藏层层数、神经元个数、学习率与迭代次数以及梯度下降方式几个方面对 DNN 的网络结构进行了优化,同时建立了模型的评价指标——最后将模型预测结果与矿区实际情况进行对比分析,基于 DNN 的多源信息预测模型可行。
参考文献:基于深度学习的多源信息找矿模型构建及应用