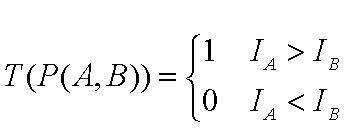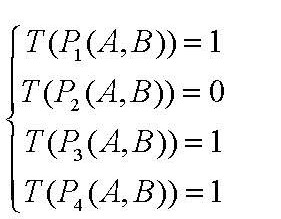文章目录
1 算法原理
1.1和1.2内容引用高翔《视觉SLAM十四讲》。
1.3内容引用:https://mp.weixin.qq.com/s/u5gSCwQ3XahF0fe19biAyQ
1.1 ORB组成
“ORB 特征亦由关键点和描述子两部分组成。它的关键点称为“Oriented FAST”,是一种改进的 FAST 角点。它的描述子称为 BRIEF(Binary Robust Independent Elementary Features)。因此,提取 ORB 特征分为两个步骤:
1)FAST 角点提取:找出图像中的” 角点”。相较于原版的 FAST, ORB 中计算了特征
点的主方向,为后续的 BRIEF 描述子增加了旋转不变特性。
2)BRIEF 描述子:对前一步提取出关键点的周围图像区域进行描述。”
1.2 FAST关键点
1.2.1 ORB检测过程
“FAST 是一种角点,主要检测局部像素灰度变化明显的地方,以速度快著称。它的思想是:如果一个像素与它邻域的像素差别较大(过亮或过暗), 那它更可能是角点。相比于其他角点检测算法,FAST 只需比较像素亮度的大小,十分快捷。它的检测过程如下(参考上图):”
1)在图像中选取像素 p,假设它的亮度为 Ip。
2)设置一个阈值 T(比如 Ip 的 20%)。
3)以像素 p 以像素p 为中心, 选取半径为3 的圆上的16 个像素点。
4)假如选取的圆上,有连续的 N 个点的亮度大于 Ip + T 或小于 Ip − T,那么像素p可以被认为是特征点 (N 通常取 12,即为 FAST-12。其它常用的 N 取值为 9 和 11,他们分别被称为 FAST-9,FAST-11)。
5)循环以上四步,对每一个像素执行相同的操作。
“在 FAST-12 算法中,为了更高效,可以添加一项预测试操作,以快速地排除绝大多数不是角点的像素。具体操作为,对于每个像素,直接检测邻域圆上的第 1,5,9,13 个像素的亮度。只有当这四个像素中有三个同时大于 Ip + T 或小于 Ip − T 时,当前像素才有可能是一个角点,否则应该直接排除。这样的预测试操作大大加速了角点检测。此外,原始的 FAST 角点经常出现“扎堆”的现象。所以在第一遍检测之后,还需要用非极大值抑制(Non-maximal suppression),在一定区域内仅保留响应极大值的角点,避免角点集中的问题。”
1.2.2 存在问题——数量多、尺度和旋转
“FAST 特征点的计算仅仅是比较像素间亮度的差异,速度非常快,但它也有一些问题。首先,FAST 特征点数量很大且不确定,而我们往往希望对图像提取固定数量的特征。因此,在 ORB 中,对原始的 FAST 算法进行了改进。我们可以指定最终要提取的角点数量N,对原始 FAST 角点分别计算 Harris 响应值(见n.2),然后选取前 N 个具有最大响应值的角点,作为最终的角点集合。”
“其次,FAST 角点不具有方向信息。而且,由于它固定取半径为 3 的圆,存在尺度问题:远处看着像是角点的地方,接近后看可能就不是角点了。针对 FAST 角点不具有方向性和尺度的弱点,ORB 添加了尺度和旋转的描述。尺度不变性由构建图像金字塔,并在金字塔的每一层上检测角点来实现。而特征的旋转是由灰度质心法(Intensity Centroid)实现的。”
1.2.3 旋转解决
质心是指以图像块灰度值作为权重的中心,圆心(几何中心)和质心的连线可以作为FAST特征点的方向。
1)在一个小的图像块 B 中,定义图像块的矩为:
m
p
q
=
∑
x
,
y
∈
B
x
p
y
q
I
(
x
,
y
)
,
p
,
q
=
{
0
,
1
}
{m_{pq}} = \sum\limits_{x,y \in B} {{x^p}{y^q}I\left( {x,y} \right)} ,{\rm{ p,q = \{ 0,1\} }}
mpq=x,y∈B∑xpyqI(x,y),p,q={0,1}
2)通过矩可以找到图像块的质心:
C
=
(
m
10
m
00
,
m
01
m
00
)
{\rm{C = }}\left( {\frac{{{m_{10}}}}{{{m_{00}}}},\frac{{{m_{01}}}}{{{m_{00}}}}} \right)
C=(m00m10,m00m01)
3)连接图像块的几何中心 O 与质心 C,得到一个方向向量 −−→OC,于是特征点的方向可以定义为:
θ
=
arctan
(
m
01
/
m
10
)
\theta = \arctan ({m_{01}}/{m_{10}})
θ=arctan(m01/m10)
“通过金字塔和质心法,FAST 角点便具有了尺度与旋转的描述,大大提升了它们在不同图像之间表述的鲁棒性。所以在 ORB 中,把这种改进后的 FAST 称为 Oriented FAST。”
1.3 BRIEF描述子
“得到特征点后我们需要以某种方式F描述这些特征点的属性。这些属性的输出我们称之为该特征点的描述子。ORB采用BRIEF算法来计算一个特征点的描述子。BRIEF算法的核心思想是在关键点P的周围以一定模式选取N个点对,把这N个点对的比较结果组合起来作为描述子。”
接下来看一下具体操作:
1)以关键点P为圆心,以d为半径做圆O。
2)在圆O内某一模式选取N个点对。这里为方便说明,N=4,实际应用中N可以取512.
3)假设当前选取的4个点对如上图所示分别标记为:
P
1
(
A
,
B
)
,
P
2
(
A
,
B
)
,
P
3
(
A
,
B
)
,
P
4
(
A
,
B
)
{P_1}(A,B),{P_2}(A,B),{P_3}(A,B),{P_4}(A,B)
P1(A,B),P2(A,B),P3(A,B),P4(A,B)
4)定义操作T
分别对已选取的点对进行T操作,将得到的结果进行组合。
假如:
则最终的描述子为:1011
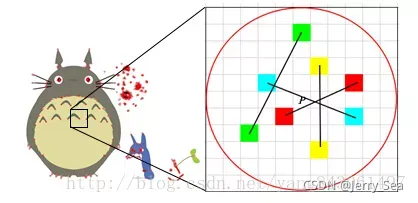
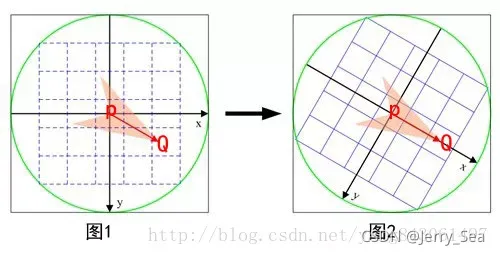
在当前关键点P周围以一定模式选取N个点对,组合这N个点对的T操作的结果就为最终的描述子。当图片不发生旋转时,我们选取点对的时候,是以当前关键点为原点,以水平方向为X轴,以垂直方向为Y轴建立坐标系。当图片发生旋转时,坐标系不变,同样的取点模式取出来的点却不一样,计算得到的描述子也不一样,这是不符合我们要求的。因此我们需要重新建立坐标系,使新的坐标系可以跟随图片的旋转而旋转。这样我们以相同的取点模式取出来的点将具有一致性。
ORB在计算BRIEF描述子时建立的坐标系是以关键点为圆心,以关键点和取点区域的形心的连线为X轴建立2维坐标系。
如下图:
总结:
“ORB算法最大的特点就是计算速度快 。 这首先得益于使用FAST检测特征点,FAST的检测速度正如它的名字一样是出了名的快。再次是使用BRIEF算法计算描述子,该描述子特有的2进制串的表现形式不仅节约了存储空间,而且大大缩短了匹配的时间。
例如特征点A、B的描述子如下:
A:10101011
B:10101010
我们设定一个阈值,比如80%。当A和B的描述子的相似度大于90%时,我们判断A,B是相同的特征点,即这2个点匹配成功。在这个例子中A,B只有最后一位不同,相似度为87.5%,大于80%。则A和B是匹配的。
我们将A和B进行异或操作就可以轻松计算出A和B的相似度。而异或操作可以借组硬件完成,具有很高的效率,加快了匹配的速度。”
1 代码实现
关键点、描述子和match实现
feature_extraction.cpp:
#include <iostream>
//#include <opencv2/core/core.hpp>
//#include <opencv2/features2d/features2d.hpp>//特征点头文件,处理特征点信息
//#include <opencv2/highgui/highgui.hpp>//opencv gui头文件
//上述三个头文件是支持opencv2版本的头文件,opencv3可以直接用下面这个语句
#include"opencv2/opencv.hpp"
#include <chrono>//用于计时的头文件
using namespace std;
using namespace cv;
int main ( int argc, char** argv )
{
// if (argc != 3) {
// cout << "usage: feature_extraction img1 img2" << endl;//读取图片文件的用法
// return 1;
// }
// //-- 读取图像
// Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);//读取彩色图片1 CV_LOAD_IMAGE_COLOR表示返回的是一张彩色图
// Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);//读取彩色图片2 CV_LOAD_IMAGE_COLOR表示返回的是一张彩色图
//-- 读取图像
Mat img_1 = imread ( "../1.png", CV_LOAD_IMAGE_COLOR ); // "../1.png" not "./1.png", 以生成的可执行文件所在位置,决定目录是"."还是".."
Mat img_2 = imread ( "../3.jpg", CV_LOAD_IMAGE_COLOR );
assert(img_1.data != nullptr && img_2.data != nullptr); //assert()为断言函数,如果它的条件返回错误,则终止程序执行
//-- 初始化
std::vector<KeyPoint> keypoints_1, keypoints_2;
Mat descriptors_1, descriptors_2;
Ptr<FeatureDetector> detector = ORB::create(); // create(1000)-> extract 1000 可以修改特征点的个数来增加匹配点数量
Ptr<DescriptorExtractor> descriptor = ORB::create();
Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create ( "BruteForce-Hamming" );
//-- 第一步:检测 Oriented FAST 角点位置
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();//检测 Oriented FAST 角点前计时
detector->detect ( img_1,keypoints_1 );
cout<<"keypoints_1.size(): "<<keypoints_1.size()<<endl;
detector->detect ( img_2,keypoints_2 );
cout<<"keypoints_2.size(): "<<keypoints_2.size()<<endl;
//-- 第二步:根据角点位置计算 BRIEF 描述子
descriptor->compute ( img_1, keypoints_1, descriptors_1 );
descriptor->compute ( img_2, keypoints_2, descriptors_2 );
cout<<"descriptors_1.size(): "<<descriptors_1.size()<<endl;
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();//计算耗时
chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);//计算检测角点和计算描述子所用的时间
cout << "extract ORB cost = " << time_used.count() << " seconds. " << endl;//输出extract ORB cost =
Mat outimg1;
drawKeypoints( img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
imshow("ORB特征点",outimg1);
//-- 第三步:对两幅图像中的BRIEF描述子进行匹配,使用 Hamming 距离
vector<DMatch> matches;
t1 = chrono::steady_clock::now();//计时
//BFMatcher matcher ( NORM_HAMMING );
matcher->match ( descriptors_1, descriptors_2, matches );
cout<<" descriptors_1.rows: "<< descriptors_1.rows<<endl;
t2 = chrono::steady_clock::now();//计时
time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);//计算耗时
cout << "match ORB cost = " << time_used.count() << " seconds. " << endl;//输出match ORB cost
//-- 第四步:匹配点对筛选
double min_dist=10000, max_dist=0;
//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
for ( int i = 0; i < descriptors_1.rows; i++ )
{
double dist = matches[i].distance;
cout<<"dist: "<<dist<<endl;
if ( dist < min_dist ) min_dist = dist;
if ( dist > max_dist ) max_dist = dist;
}
// 仅供娱乐的写法
min_dist = min_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distance<m2.distance;} )->distance; //minmax_element()为c++中定义的寻找最小值和最大值的函数。
max_dist = max_element( matches.begin(), matches.end(), [](const DMatch& m1, const DMatch& m2) {return m1.distance<m2.distance;} )->distance;
printf ( "-- Max dist : %f \n", max_dist );
printf ( "-- Min dist : %f \n", min_dist );
//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
std::vector< DMatch > good_matches;
for ( int i = 0; i < descriptors_1.rows; i++ )
{
if ( matches[i].distance <= max ( 2*min_dist, 30.0 ) )
{
good_matches.push_back ( matches[i] );
}
}
//-- 第五步:绘制匹配结果
Mat img_match;
Mat img_goodmatch;
drawMatches ( img_1, keypoints_1, img_2, keypoints_2, matches, img_match );
drawMatches ( img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch );
imshow ( "所有匹配点对", img_match );
imshow ( "优化后匹配点对", img_goodmatch );
waitKey(0);
return 0;
}
n 补充
n.1 Sobel
原理参考:
https://www.cnblogs.com/feifanrensheng/p/8047420.html
https://blog.csdn.net/dcrmg/article/details/52280768
demo:
算法实现和cv::Sobel使用对比
#include "core/core.hpp"
#include "highgui/highgui.hpp"
#include "imgproc/imgproc.hpp"
#include "iostream"
using namespace std;
using namespace cv;
int main(int argc, char *argv[])
{
Mat image = imread("lena.bmp", 0);
Mat imageX = Mat::zeros(image.size(), CV_16SC1);
Mat imageY = Mat::zeros(image.size(), CV_16SC1);
Mat imageXY = Mat::zeros(image.size(), CV_16SC1);
Mat imageX8UC;
Mat imageY8UC;
Mat imageXY8UC;
if (!image.data)
{
return -1;
}
GaussianBlur(image, image, Size(3, 3), 0); //高斯滤波消除噪点
uchar *P = image.data;
uchar *PX = imageX.data;
uchar *PY = imageY.data;
int step = image.step; //step一行占几个字节?
int stepXY = imageX.step;
for (int i = 1; i < image.rows - 1; i++)
{
for (int j = 1; j < image.cols - 1; j++)
{
//通过指针遍历图像上每一个像素
PX[i*imageX.step + j * (stepXY / step)] = abs(P[(i - 1)*step + j + 1] + P[i*step + j + 1] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[i*step + j - 1] * 2 - P[(i + 1)*step + j - 1]);
PY[i*imageX.step + j * (stepXY / step)] = abs(P[(i + 1)*step + j - 1] + P[(i + 1)*step + j] * 2 + P[(i + 1)*step + j + 1] - P[(i - 1)*step + j - 1] - P[(i - 1)*step + j] * 2 - P[(i - 1)*step + j + 1]);
}
}
addWeighted(imageX, 0.5, imageY, 0.5, 0, imageXY);//融合X、Y方向
//可以加上下面这几句话
//normalize(imageX, imageX, 0, 255, NORM_MINMAX, CV_16SC1, Mat());
//normalize(imageY, imageY, 0, 255, NORM_MINMAX, CV_16SC1, Mat());
//normalize(imageXY, imageXY, 0, 255, NORM_MINMAX, CV_16SC1, Mat())
convertScaleAbs(imageX, imageX8UC);
convertScaleAbs(imageY, imageY8UC);
convertScaleAbs(imageXY, imageXY8UC); //转换为8bit图像
Mat imageSobel_x, imageSobel_y,imageSobel;
Sobel(image, imageSobel_x, CV_8UC1, 1, 0); //Opencv的Sobel函数
Sobel(image, imageSobel_y, CV_8UC1, 0, 1); //CV_8UC1 -> -1,-1的意思是和输入图片一致
//扩展Sobel核的大小,必须是 1, 3, 5 或 7。 除了尺寸为 1, 其它情况下, aperture_size ×aperture_size 可分离内核将用来计算差分。
//对 aperture_size = 1的情况, 使用 3x1 或 1x3 内核 (不进行高斯平滑操作)。
//这里有一个特殊变量 CV_SCHARR(= -1),对应 3x3 Scharr 滤波器,可以给出比 3x3 Sobel 滤波更精确的结果。
/*
-1 0 1
Gx = -2 0 2
-1 0 1
变为:
-3 0 3
Gx = -10 0 10
-3 0 3
*/
addWeighted(imageSobel_x, 0.5, imageSobel_y, 0.5, 0, imageSobel);
imshow("Source Image", image);
imshow("X Direction", imageX8UC);
imshow("Y Direction", imageY8UC);
imshow("XY Direction", imageXY8UC);
imshow("Opencv Sobel", imageSobel);
waitKey();
return 0;
}
n.2 Harris
1)Harris角点检测原理
补充:
det
M
=
λ
1
λ
2
=
A
C
−
B
2
t
r
a
c
e
M
=
λ
1
+
λ
2
=
A
+
C
\begin{array}{l} \det M = {\lambda _1}{\lambda _2} = AC - {B^2}\\ traceM = {\lambda _1} + {\lambda _2} = A + C \end{array}
detM=λ1λ2=AC−B2traceM=λ1+λ2=A+C
特征值的和等于矩阵主对角线上元素之和
特征值之积等于矩阵行列式?
2)demo1.cpp
直接使用opencv Harris角点检测函数调用
常调用三个函数:
- cornerHarris(gray_src, dst, 2, 3, 0.04, BORDER_DEFAULT);
normalize(dst, norm_dst, 0, 255, NORM_MINMAX, CV_32FC1, Mat()); //normalize函数是将数据归一化到一个范围,数据类型可以不用改变
convertScaleAbs(norm_dst, norm_dst); //convertScaleAbs函数是将dst(I)=saturate(|src(I)*alpha+beta|),转为uchar类型
#include"opencv2/opencv.hpp"
#include<iostream>
#include<math.h>
using namespace cv;
using namespace std;
void Harris_demo(int, void*);
int thres_value = 130;
int thres_Max = 255;
Mat src, gray_src;
const char* outputTitle = "output title";
int main(int argc, char** argv)
{
src = imread("big.png");
if (src.empty())
{
cout << "图片为空" << endl;
return -1;
}
cvtColor(src, gray_src, CV_BGR2GRAY);
namedWindow(outputTitle, CV_WINDOW_AUTOSIZE);
createTrackbar("Harris", outputTitle, &thres_value, thres_Max, Harris_demo);
Harris_demo(0, 0);
imshow("input title", src);
waitKey(0);
return 0;
}
void Harris_demo(int, void *)
{
Mat dst, norm_dst;
dst = Mat::zeros(gray_src.size(), CV_32FC1);
//求Harris角点得分图
cornerHarris(gray_src, dst, 2, 3, 0.04, BORDER_DEFAULT);
normalize(dst, norm_dst, 0, 255, NORM_MINMAX, CV_32FC1, Mat());
convertScaleAbs(norm_dst, norm_dst);
Mat resultImg = src.clone();
//显示大于阈值的角点
for (int row = 0; row < resultImg.rows; row++)
{
uchar* currentRow = norm_dst.ptr(row);
for (int col = 0; col < resultImg.cols; col++)
{
int value = (int)*currentRow;
if (value > thres_value)
{
circle(resultImg, Point(col, row), 2, Scalar(0, 0, 255), 2, 8, 0);
}
currentRow++;
}
}
imshow(outputTitle, resultImg);
}
3)demo2.cpp
opencv Harris角点检测源码实现
#include "opencv2/opencv.hpp"
#include <iostream>
#include <stdio.h>
#include <stdlib.h>
using namespace cv;
using namespace std;
/// Global variables
Mat src, src_gray;
int thresh = 200;
int max_thresh = 255;
const char* source_window = "Source image"; //赋值的数组是字符串指针数组,而定义的却是字符数组。字符串类型是常量,"Source image"是常量,所以用const char*
const char* corners_window = "Corners detected";
/// Function header
void cornerHarris_demo(int, void*);
void myHarris(const Mat& src, Mat& eigenv, int block_size, int aperture_size, double k = 0.);
/** @function main */
int main(int argc, char** argv)
{
/// Load source image and convert it to gray
//src = imread(argv[1], 1);
src = imread("lena.bmp", 1);
cvtColor(src, src_gray, CV_BGR2GRAY);
Mat image = src;
Mat gray;
cvtColor(image, gray, CV_BGR2GRAY);
/// Create a window and a trackbar
namedWindow(source_window, CV_WINDOW_AUTOSIZE);
createTrackbar("Threshold: ", source_window, &thresh, max_thresh, cornerHarris_demo);
imshow(source_window, src);
cornerHarris_demo(0, 0);
waitKey(0);
return(0);
}
/** @function cornerHarris_demo */
void cornerHarris_demo(int, void*)
{
Mat dst, dst_norm, dst_norm_scaled;
dst = Mat::zeros(src.size(), CV_32FC1);
/// Detector parameters
int blockSize = 2;
int apertureSize = 3;
double k = 0.04;
/// Detecting corners
//cornerHarris(src_gray, dst, blockSize, apertureSize, k, BORDER_DEFAULT);
myHarris(src_gray, dst, blockSize, apertureSize, k);
/// Normalizing
normalize(dst, dst_norm, 0, 255, NORM_MINMAX, CV_32FC1, Mat());//这里CV_32FC1也可以写成-1,意味着dst_norm输出的类型和dst类型相同
convertScaleAbs(dst_norm, dst_norm_scaled);
//normalize函数是将数据归一化到一个范围,数据类型可以不用改变
//convertScaleAbs函数是将dst(I)=saturate<uchar>(|src(I)*alpha+beta|)
/// Drawing a circle around corners
for (int j = 0; j < dst_norm.rows; j++)
{
for (int i = 0; i < dst_norm.cols; i++)
{
if ((int)dst_norm.at<float>(j, i) > thresh)
{
circle(dst_norm_scaled, Point(i, j), 5, Scalar(0), 2, 8, 0);
}
}
}
/// Showing the result
namedWindow(corners_window, CV_WINDOW_AUTOSIZE);
imshow(corners_window, dst_norm_scaled);
}
/*Harris角点实现函数,截取cornerHarris中的关键代码并做了简化....*/
void myHarris(const Mat& src, Mat& eigenv, int block_size, int aperture_size, double k)
{
eigenv.create(src.size(), CV_32F);
Mat Dx, Dy;
//sobel operation get Ix, Iy
Sobel(src, Dx, CV_32F, 1, 0, aperture_size);
Sobel(src, Dy, CV_32F, 0, 1, aperture_size);
//get covariance matrix
Size size = src.size();
Mat cov(size, CV_32FC3); //创建一个三通道cov矩阵分别存储[Ix*Ix, Ix*Iy; Iy*Ix, Iy*Iy];
for (int i = 0; i < size.height; i++)
{
float* cov_data = cov.ptr<float>(i);
const float* dxdata = Dx.ptr<float>(i);
const float* dydata = Dy.ptr<float>(i);
for (int j = 0; j < size.width; j++)
{
float dx = dxdata[j];
float dy = dydata[j];
cov_data[j * 3] = dx * dx; //即 Ix*Ix
cov_data[j * 3 + 1] = dx * dy; //即 Ix*Iy
cov_data[j * 3 + 2] = dy * dy; //即 Iy*Iy
}
}
//方框滤波 W(x,y)卷积,也可用高斯核加权...
//W(X,Y)与矩阵cov卷积运算得到 H 矩阵,后面通过H矩阵的特征值决定是否是角点
boxFilter(cov, cov, cov.depth(), Size(block_size, block_size), Point(-1, -1), false);
//cale Harris
size = cov.size();
if (cov.isContinuous() && eigenv.isContinuous())
{
size.width *= size.height;
size.height = 1;
//cout << "yes"<< size.height << endl;
}
//此处计算响应R= det(H) - k*trace(H)*trace(H);
for (int i = 0; i < size.height; i++)
{
const float* covPtr = cov.ptr<float>(i);
float* dstPtr = eigenv.ptr<float>(i);
for (int j = 0; j < size.width; j++)
{
float a = covPtr[j * 3];
float b = covPtr[j * 3 + 1];
float c = covPtr[j * 3 + 2];
//根据公式 R = det(H) - k* trace(H)*trace(H);
dstPtr[j] = (float)(a*c - b * b - k * (a + c)*(a + c));
}
}
}
n.3 boxFilter
boxFilter原理
盒式滤波是一种非常有用的线性滤波,也叫方框滤波,最简单的均值滤波就是盒子滤波归一化的情况。(归一化就是除以卷积核大小——宽x高)
n.2中上述例子中,Harris角点检测blocksize设置2。2也是可以的,不一定是3、5。取左、上、左上,四个点的位置,按单独通道相加。边缘点的值取向内一行的值。(第0行/列取1行/列,第n行/列取第n-1行/列),具体操作可看下图。
卷积前:
卷积后: