矩阵连乘 - 悦读

动态规划基本思想:将待求解问题分解成若干个不独立的子问题求出子问题的解并记录其表中当需要再次求解次子问题时可以通过查表获得该子问题的解而不用再次求解从而避免大量重复计算最后这些子问题即可得到原问题的解
动态规划法的解题思路:
①分析问题的最优子结构性质:一个最优策略的子策略总最优
②建立递归关系
③自下而上计算最优值
④根据计算最优值时得到的信息,构造最优解
下面给出矩阵连乘问题:
给定n个矩阵{A $_ {1}$ ,A $_ {2}$ ,A $_ {3}$ …A $_ {n}$ }其中A $_ {i}$ 与A $_ {i+1}$ 是可乘的(i=1,2…n-1),由于矩阵乘法满足结合律,所以矩阵连乘有不同的运算次序,矩阵连乘问题就是确定计算矩阵连乘积的计算次序,使得依此次序计算矩阵的数乘次数最少。输入数据为矩阵的个数和每个矩阵的规模,输出结果为计算矩阵连乘积的计算次序和最少数乘次数
将矩阵连乘A $_ {i}$ A $_ {i+1}$ …A $_ {j}$ 简记为A[i:j](i≤j) A $_ {i}$ 维度记为p $_ {i-1}$ *p $_ {i}$
如:给定三个矩阵A $_ {1}$ 、A $_ {2}$ 、A $_ {3}$
在这里插入图片描述
易知有两种运算次序:(A $_ {1}$ *A $_ {2}$ )*A $_ {3}$ 和A $_ {1}$ *(A $_ {2}$ *A $_ {3}$ )
第一种次序运算次数为(2:3 3:2)2:4=2*3*2=12→(2:2 2:4)=2*2*4=16 总次数为12+16=28
第二种次序运算次数为2:3(3:2 2:4)=3*2*4=24→(2:3 3:4)=2*3*4=24 总次数为24+24=48
▲分析:若存在一个计算A[1:k]的次序所需的计算量(相对于之前求得的最优解)更少则取代之类似地,计算A[k+1:n]的次序也一定是最优的。由此可知矩阵连乘计算次序问题的最优解包含了其子问题的最优解。
那么计算目的是求解A[1:n]的最优解,而一个最优策略的子策略也应是最优的,所以问题可分解为求A[i:j](1≤i≤j≤n)的最优计算次序。
计算A[i:j]的最优计算次序:设这个计算次序在矩阵A $_ {k}$ 和A $_ {k+1}$
之间将矩阵链断开(i≤k<j) 则其相应加括号形式为:(A $_ {i}$ A $_ {i+1}$ …A $_ {k}$ )(A $_ {k+1}$ A $_ {k+2}$ …A $_ {j}$ ) 那么A[i:j]的计算量为A[i:k]的计算量加上A[k+1:j]的计算量再加上A[i:k]和A[k+1:j]相乘的计算量。
建立递归关系:设计算A[i:j](1≤i≤j≤n)所需要的最少乘次数dp[i][j] 则原问题的最优值为dp[1][n]
当i=j时(矩阵只有一个),A[i:j]=A $_ {i}$ 因此dp[i][i]=0
当i<j时 A $_ {i}$ 的维数为p $_ {i-1}$ *p $_ {i}$
由此可得递归关系:
当i=j时 dp[i][j]=0
当i<j时 dp[i][j]=min $_ {i≤k<j}$ (dp[i][k]+dp[k+1][j]+p $_ {i-1}$ *p $_ {k}$ *p $_ {j}$ )

#include<bits/stdc++.h>
using namespace std;
const long long MAX=1e10+2;
const int N=102;
int p[N];//保存各矩阵的维数 
long long s[N][N],dp[N][N];//s存储切割位置 dp存储最优值 
void MChain(int n){
	for(int i=0;i<n+1;i++)//赋初值 
		for(int j=0;j<n+1;j++){
			dp[i][j]=MAX;
			s[i][j]=0;
		}		
	for(int i=0;i<=n;i++){
		cin>>p[i];
		dp[i][i]=0;//只有一个矩阵时最优值为0
	}
	for(int L=2;L<=n;L++){//相乘矩阵的个数 
		for(int i=1;i<=n;i++){ 
			int j=i+L-1;
			if(j>n) break; //越界 
			for(int k=i;k<j;k++){//遍历切割位置
				int MIN=dp[i][j];
				int temp=dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j];
				if(temp<MIN){
					dp[i][j]=temp;
					MIN=temp;
					s[i][j]=k;
				}
			//dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+p[i-1]*p[k]*p[j]);
			}
		}
	}
}
void Traceback(int i,int j){
	if(i==j) return;
	int k=s[i][j];
	Traceback(i,k);//左半部分 
	Traceback(k+1,j);//右半部分 
	cout<<"A["<<i<<":"<<k<<"]*A["<<k+1<<":"<<j<<"]"<<endl;
}
int main(int argc, char** argv)
{
	int n; 
	cin>>n;	
	MChain(n);
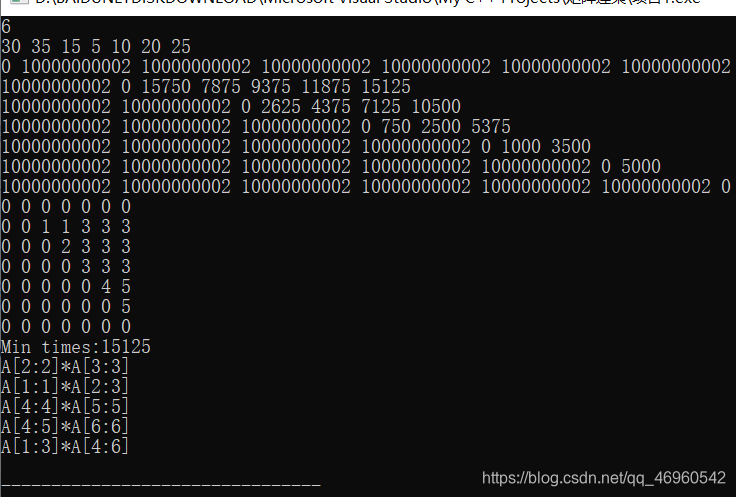
	//输出dp表	
	for(int i=0;i<=n;i++){
		for(int j=0;j<=n;j++)
			cout<<dp[i][j]<<" ";
		cout<<endl;
	}	
	//输出s表 
	for(int i=0;i<=n;i++){
		for(int j=0;j<=n;j++)
			cout<<s[i][j]<<" ";
		cout<<endl;
	}	 
	cout<<"Min times:"<<dp[1][n]<<endl;
	Traceback(1,n);
	return 0;
}

在这里插入图片描述
时间复杂度分析:MChain函数包含三重循环,循环体内计算量O(1) 故该算法时间复杂度为O( $n^3$ ),空间复杂度O( $n^2$ )。所以动态规划法远比穷举法有效。