决策树

关于CART与ID3,C4.5的区别和联系

知识点

参考：决策树CART与ID3,C4.5联系与区别

代码

# coding=utf-8

import numpy as np

class DTreeID3(object):

    def __init__(self, epsilon=0.0001):
        self.tree = Node()
        self.epsilon = epsilon

    def fit(self, X_train, Y_train):
        A_recorder = np.arange(X_train.shape[1])
        self._train(X_train, Y_train, self.tree, A_recorder)

    def predict(self, X):
        n = X.shape[0]
        Y = np.zeros(n)
        for i in range(n):
            Y[i] = self.tree.predict_classification(X[i, :])
        return Y

    def visualization(self):
        return self._visualization_dfs(self.tree)

    def _train(self, A, D, node, AR):
        # 1. 结束条件：若 D 中所有实例属于同一类，决策树成单节点树，直接返回
        if np.any(np.bincount(D) == len(D)):
            node.y = D[0]
            return
        # 2. 结束条件：若 A 为空，则返回单结点树 T，标记类别为样本默认输出最多的类别
        if A.size == 0:
            node.y = np.argmax(np.bincount(D))
            return
        # 3. 计算特征集 A 中各特征对 D 的信息增益，选择信息增益最大的特征 A_g
        max_info_gain, g = self._feature_choose_standard(A, D)
        # 4. 结束条件：如果 A_g 的信息增益小于阈值 epsilon，决策树成单节点树，直接返回
        if max_info_gain <= self.epsilon:
            node.y = np.argmax(np.bincount(D))
            return
        # 5. 对于 A_g 的每一可能值 a_i，依据 A_g = a_i 将 D 分割为若干非空子集 D_i，将当前结点的标记设为样本数最大的 D_i 对应
            # 的类别，即对第 i 个子节点，以 D_i 为训练集，以 A - {A_g} 为特征集，递归调用以上步骤，得到子树 T_i，返回 T_i
        node.label = AR[g]
        a_cls = np.bincount(A[:, g])
        new_A, AR = np.hstack((A[:, 0:g], A[:, g+1:])), np.hstack((AR[0:g], AR[g+1:]))
        for k in range(len(a_cls)):
            a_row_idxs = np.argwhere(A[:, g] == k).T[0].T
            child = Node(k)
            node.append(child)
            A_child, D_child = new_A[a_row_idxs, :], D[a_row_idxs]
            self._train(A_child, D_child, child, AR)

    def _feature_choose_standard(self, A, D):
        row, col = A.shape
        prob = self._cal_prob(D)
        prob = np.array([a if 0 < a <= 1 else 1 for a in prob])
        entropy = -np.sum(prob * np.log2(prob))
        max_info_gain_ratio = None
        g = None
        for j in range(col):
            a_cls = np.bincount(A[:, j])
            condition_entropy = 0
            for k in range(len(a_cls)):
                a_row_idxs = np.argwhere(A[:, j] == k)
                # H(D)
                prob = self._cal_prob(D[a_row_idxs].T[0])
                prob = np.array([a if 0 < a <= 1 else 1 for a in prob])
                H_D = -np.sum(prob * np.log2(prob))
                # H(D|A)=SUM(p_i * H(D|A=a_i))
                condition_entropy += a_cls[k] / np.sum(a_cls) * H_D
            feature_choose_std = entropy - condition_entropy
            if max_info_gain_ratio is None or max_info_gain_ratio < feature_choose_std:
                max_info_gain_ratio = feature_choose_std
                g = j
        return max_info_gain_ratio, g

    def _cal_prob(self, D):
        statistic = np.bincount(D)
        prob = statistic / np.sum(statistic)
        return prob

    def _visualization_dfs(self, node, layer=0):
        prefix = '\n' if layer else ''
        output_str = [prefix + ' ' * 4 * layer, '%r+%r ' % (node.y, node.label)]
        if not node.child:
            return ''.join(output_str)
        for child in node.child:
            output_str.append(self._visualization_dfs(child, layer=layer + 1))
        return ''.join(output_str)

class DTreeC45(DTreeID3):

    def _feature_choose_standard(self, A, D):
        row, col = A.shape
        prob = self._cal_prob(D)
        prob = np.array([a if 0 < a <= 1 else 1 for a in prob])
        entropy = -np.sum(prob * np.log2(prob))
        max_info_gain_ratio = None
        g = None
        for j in range(col):
            a_cls = np.bincount(A[:, j])
            condition_entropy = 0
            for k in range(len(a_cls)):
                a_row_idxs = np.argwhere(A[:, j] == k)
                # H(D) = -SUM(p_i * log(p_i))
                prob = self._cal_prob(D[a_row_idxs].T[0])
                prob = np.array([a if 0 < a <= 1 else 1 for a in prob])
                H_D = -np.sum(prob * np.log2(prob))
                # H(D|A)=SUM(p_i * H(D|A=a_i))
                condition_entropy += a_cls[k] / np.sum(a_cls) * H_D
            feature_choose_std = entropy / (condition_entropy + 0.0001)
            if max_info_gain_ratio is None or max_info_gain_ratio < feature_choose_std:
                max_info_gain_ratio = feature_choose_std
                g = j
        return max_info_gain_ratio, g

class DTreeCART(DTreeID3):

    def _train(self, A, D, node, AR):
        self.visited_set = set()
        self._train_helper(A, D, node, AR)

    def _train_helper(self, A, D, node, AR):
        # 1. 结束条件：若 D 中所有实例属于同一类，决策树成单节点树，直接返回
        if np.any(np.bincount(D) == len(D)):
            node.y = D[0]
            return
        # 2. 与 ID3, C4.5 不一样, 不会直接去掉 A
        if A.size == 0:
            node.y = np.argmax(np.bincount(D))
            return
        # 3. 与 ID3, C4.5 不一样, 不仅要确定最优切分特征，还要确定最优切分值
        max_info_gain, g, v, a_idx, other_idx = self._feature_choose_standard(A, D)
        if (g, v) in self.visited_set:
            node.y = np.argmax(np.bincount(D))
            return
        self.visited_set.add((g, v))
        # 4. 结束条件：如果 A_g 的信息增益小于阈值 epsilon，决策树成单节点树，直接返回
        if max_info_gain <= self.epsilon:
            node.y = np.argmax(np.bincount(D))
            return
        # 5. 与 ID3, C4.5 不一样, 不是 len(a_cls) 叉树，而是二叉树
        node.label = AR[g]
        idx_list = a_idx, other_idx
        for k, row_idx in enumerate(idx_list):
            row_idx = row_idx.T[0].T
            child = Node(k)
            node.append(child)
            A_child, D_child = A[row_idx, :], D[row_idx]
            self._train_helper(A_child, D_child, child, AR)

    def _feature_choose_standard(self, A, D):
        row, col = A.shape
        min_gini, g, v, a_idx, other_idx = None, None, None, None, None
        for j in range(col):
            a_cls = np.bincount(A[:, j])
            # 与 ID3, C4.5 不一样,不仅要确定最优切分特征，还要确定最优切分值
            for k in range(len(a_cls)):
                # 根据切分值划为两类
                a_row_idxs, other_row_idxs = np.argwhere(A[:, j] == k), np.argwhere(A[:, j] != k)
                # H(D) = -SUM(p_i * log(p_i))
                a_prob, other_prob = self._cal_prob(D[a_row_idxs].T[0]), self._cal_prob(D[other_row_idxs].T[0])
                a_gini_D, other_gini = 1 - np.sum(a_prob * a_prob), 1 - np.sum(other_prob * other_prob)
                # H(D|A)=SUM(p_i * H(D|A=a_i))
                gini_DA = a_cls[k] / np.sum(a_cls) * a_gini_D + (1 - a_cls[k] / np.sum(a_cls)) * other_gini
                if min_gini is None or min_gini > gini_DA:
                    min_gini, g, v, a_idx, other_idx = gini_DA, j, k, a_row_idxs, other_row_idxs

        return min_gini, g, v, a_idx, other_idx

class DTreeRegressionCART(object):

    def __init__(self, max_depth=1):
        self.tree = Node()
        self.max_depth = max_depth

    def fit(self, X_train, Y_train):
        A_recorder = np.arange(X_train.shape[1])
        self._train(X_train, Y_train, self.tree, A_recorder)

    def predict(self, X):
        n = X.shape[0]
        Y = np.zeros(n)
        for i in range(n):
            Y[i] = self.tree.predict_regression(X[i, :])
        return Y

    def _train(self, A, D, node, AR, depth=0):
        # 1. 结束条件：到最后一层 | A 或 D 一样
        if depth == self.max_depth or np.all(D == D[0]) or np.all(A == A[0]):
            node.y = np.mean(D)
            return
        # 2. 选择第j个变量A_j（切分变量splitting variable）和 切分点s（splitting point）
        min_f, min_j, min_s, min_idx1, min_idx2 = None, None, None, None, None
        row, col = A.shape
        for j in range(col):
            a_col = A[:, j]
            # 这里实现比较简化，s 就直接取最值的平均数
            s = (np.max(a_col) + np.min(a_col)) * 0.5
            R1_idx, R2_idx = np.argwhere(a_col <= s).T[0], np.argwhere(a_col > s).T[0]
            if R1_idx.size == 0 or R2_idx.size == 0:
                continue
            c1, c2 = np.mean(D[R1_idx]), np.mean(D[R2_idx])
            f1, f2 = np.sum(np.square(D[R1_idx] - c1)), np.sum(np.square(D[R2_idx] - c2))
            if min_f is None or min_f > f1 + f2:
                min_f, min_j, min_s, min_idx1, min_idx2 = f1 + f2, j, s, R1_idx, R2_idx
        if min_f is None:
            node.y = np.mean(D)
            return
        # 3. 向下一层展开
        node.label, node.s = AR[min_j], min_s
        for i, idx_list in enumerate((min_idx1, min_idx2)):
            child = Node(i)
            node.append(child)
            self._train(A[idx_list, :], D[idx_list], child, AR, depth+1)

    def visualization(self):
        return self._visualization_dfs(self.tree)

    def _visualization_dfs(self, node, layer=0):
        prefix = '\n' if layer else ''
        output_str = [prefix + ' ' * 4 * layer, '%r+%r+%r' % (node.y, node.label, node.s)]
        if not node.child:
            return ''.join(output_str)
        for child in node.child:
            output_str.append(self._visualization_dfs(child, layer=layer + 1))
        return ''.join(output_str)

class Node(object):

    def __init__(self, x=None):
        self.label = None
        self.x = x
        self.s = None  # Number
        self.child = []
        self.y = None
        self.data = None

    def append(self, child):
        self.child.append(child)

    def predict_classification(self, features):
        if self.y is not None:
            return self.y
        for child in self.child:
            if child.x == features[self.label]:
                return child.predict_classification(features)
        return self.child[1].predict_classification(features)

    def predict_regression(self, features):
        if self.y is not None:
            return self.y
        child_idx = 0 if features[self.label] <= self.s else 1
        return self.child[child_idx].predict_regression(features)


datalabel = np.array(['年龄(特征1)', '有工作(特征2)', '有自己的房子(特征3)', '信贷情况(特征4)', '类别(标签)'])
train_sets = np.array([
                    ['青年', '否', '否', '一般', '否'],
                    ['青年', '否', '否', '好', '否'],
                    ['青年', '是', '否', '好', '是'],
                    ['青年', '是', '是', '一般', '是'],
                    ['青年', '否', '否', '一般', '否'],
                    ['中年', '否', '否', '一般', '否'],
                    ['中年', '否', '否', '好', '否'],
                    ['中年', '是', '是', '好', '是'],
                    ['中年', '否', '是', '非常好', '是'],
                    ['中年', '否', '是', '非常好', '是'],
                    ['老年', '否', '是', '非常好', '是'],
                    ['老年', '否', '是', '好', '是'],
                    ['老年', '是', '否', '好', '是'],
                    ['老年', '是', '否', '非常好', '是'],
                    ['老年', '否', '否', '一般', '否'],
                    ['青年', '否', '否', '一般', '是']])
map_table = {'青年': 0, '中年': 1, '老年': 2,
             '否': 0, '是': 1,
             '一般': 0, '好': 1, '非常好': 2}

if __name__ == '__main__':
    row_, col_ = train_sets.shape
    train_sets_encode = np.array([[map_table[train_sets[i, j]] for j in range(col_)] for i in range(row_)])
    X_t, Y_t = train_sets_encode[:, :-1], train_sets_encode[:, -1]
    for model in (DTreeID3(), DTreeC45(), DTreeCART()):
        model.fit(X_t, Y_t)
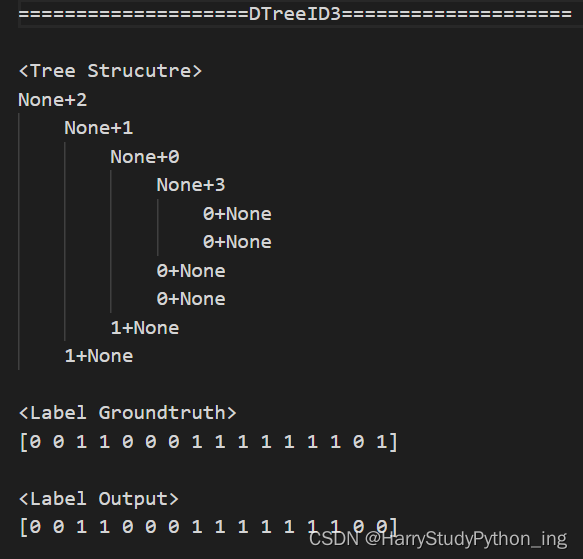
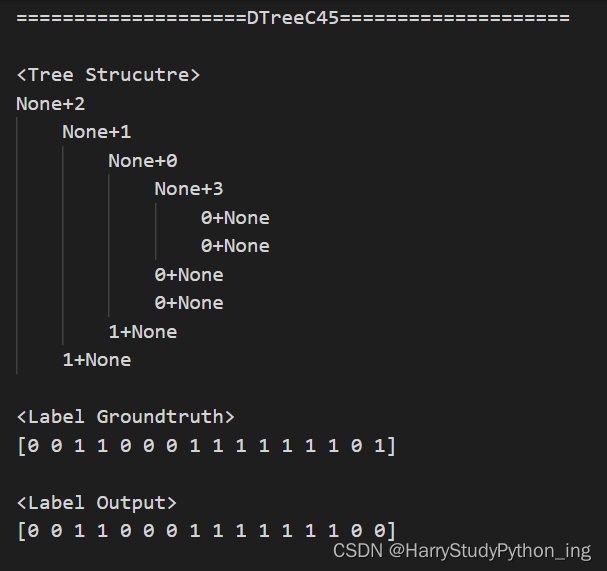
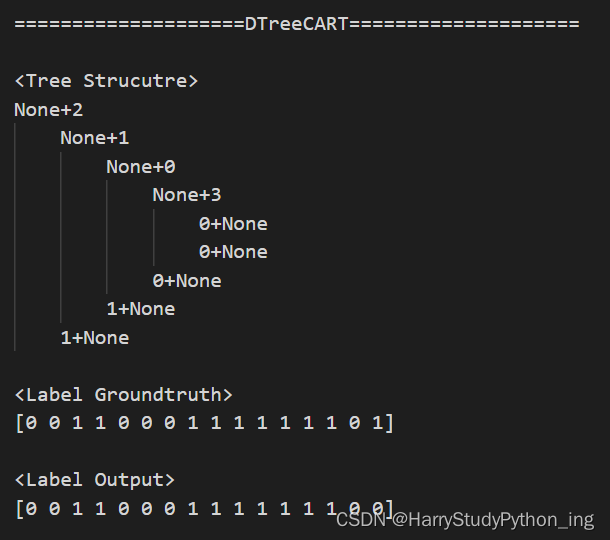
        print('=' * 20 + model.__class__.__name__ + '=' * 20)
        print('\n<Tree Strucutre>')
        print(model.visualization())
        print('\n<Label Groundtruth>')
        print(Y_t)
        print('\n<Label Output>')
        print(model.predict(X_t).astype(int))
        print()

    model = DTreeRegressionCART(max_depth=2)
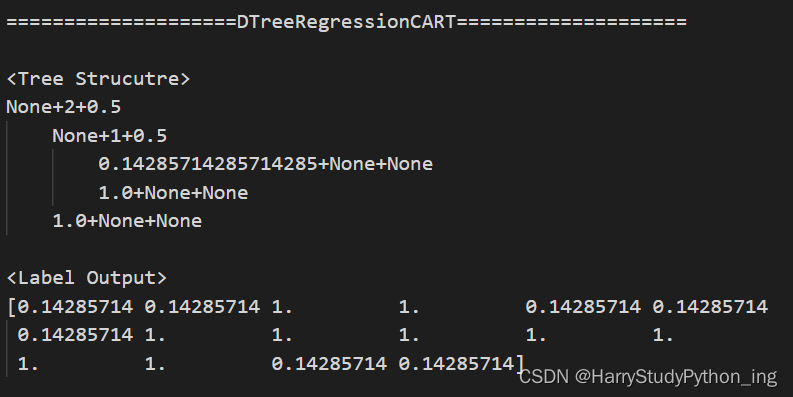
    print('=' * 20 + model.__class__.__name__ + '=' * 20)
    model.fit(X_t, Y_t)
    print('\n<Tree Strucutre>')
    print(model.visualization())
    print('\n<Label Output>')
    print(model.predict(X_t))

输出