前言
今天是学习回溯算法的第二天,从昨天的学习中我们可以知道回溯算法也有一套逻辑格式,我们对题目进行对应格式的逻辑分析即可,希望博主记录的内容能够对大家有所帮助 ,一起加油吧朋友们!💪💪💪
组合总和
这道题目是给一个无重复数的整数数组 candidates 和一个目标和 target ,然后要求找到candidates中的所有不同组合,组合的数和为target, candidates 中的数可以在组合中重复出现。
我们来梳理一下逻辑
- 使用回溯法 从
candidates中每次选择一个数字加入当前组合,然后在递归过程中保持当前组合的和不超过target🤔如果组合的和等于target,则将其加入结果集。每次选择一个数字后,允许继续选择该数字(因为同一个数字可以重复使用),但不允许选择比当前数字更小的数字(避免重复组合)🤔 通过回溯和剪枝,避免无效的组合,直到找出所有符合条件的组合🤔
我们进一步来梳理回溯三要素
- 确定递归的参数和返回值
List<List<Integer>> result = new ArrayList<>();//结果集
List<Integer> path = new ArrayList<>();//组合
private void backtracking(int[] candidates, int target, int startIndex){}
- 回溯的终止条件
int sum = path.stream().mapToInt(Integer::intValue).sum();
if(sum > target) return;
if(sum == target){
result.add(new ArrayList<>(path));//添加组合副本
return;
}
- 单层搜索过程
for(int i = startIndex; i < candidates.length; i++){
path.add(candidates[i]);//添加到组合中
backtracking(candidates, target, i);//这里不是i+1是指往下递归选取组合时可以选取重复的数
path.removeLast();//回溯
}
回溯的完整代码如下
/**未剪枝 */
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
backtracking(candidates, target, 0);
return result;
}
private void backtracking(int[] candidates, int target, int startIndex){
int sum = path.stream().mapToInt(Integer::intValue).sum();
if(sum > target) return;
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex; i < candidates.length; i++){
path.add(candidates[i]);
backtracking(candidates, target, i);
path.removeLast();
}
}
}
这里我们再来进行剪枝,对数组进行升序排序,在搜索时若提前发现已存组合和要添加的数和超出target则不进行搜索🤔🤔🤔
/**剪枝 */
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);//升序为了剪掉不必要的搜索过程
backtracking(candidates, target, 0);
return result;
}
private void backtracking(int[] candidates, int target, int startIndex){
int sum = path.stream().mapToInt(Integer::intValue).sum();
if(sum > target) return;
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){//和大于target的搜索过程剪掉
path.add(candidates[i]);
backtracking(candidates, target, i);
path.removeLast();
}
}
}
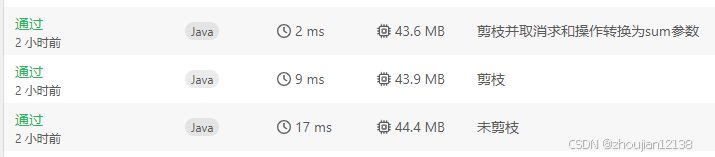
可以看到剪枝前后的速度有所提升
但实际上速度还能有所提升,可以把每次对组合的求和操作转换为递归的参数传入,递归时更新组合和这个参数即可🤔🤔🤔
/**剪枝并增加sum参数 */
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
Arrays.sort(candidates);//升序为了剪掉不必要的搜索过程
backtracking(candidates, target, 0, 0);
return result;
}
private void backtracking(int[] candidates, int target, int sum,int startIndex){
if(sum == target){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex; i < candidates.length; i++){
if(sum + candidates[i] > target) break;//和大于target的搜索过程剪掉
path.add(candidates[i]);
backtracking(candidates, target, sum+ candidates[i], i);
path.removeLast();
}
}
}
组合总和II
这道题也是给定一个整数数组candidates,从其中选取数字组合使得其的和为目标和等于所给的target,但是数字不能重复啦,每个数字只能使用一次
我们来梳理思路
- 我们先对
candidates进行排序,方便在递归中去重🤔 从第一个数字开始,每次选择一个数字加入当前组合,然后在递归过程中,如果发现当前数字与前一个数字相同,跳过该数字,避免生成重复组合🤔 如果组合的和等于target,则将该组合加入结果集。如果和超过target,则终止当前递归路径🤔 在递归返回时,移除最后一个加入的数字,尝试新的组合路径🤔
我们来梳理回溯三要素
- 确定递归的参数和返回值
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int sum = 0;//用来存组合的和
private void backTracking(int[] candidates, int target, int startIndex){}
- 回溯的终止条件(这里把判断和的大小的处理放在单层搜索过程的剪枝处理中)
if(sum == target){
result.add(new ArrayList<>(path));
}
- 单层搜索过程
for(int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){
if(i > startIndex && candidates[i] == candidates[i - 1])continue;
sum += candidates[i];
path.add(candidates[i]);
backTracking(candidates, target, i + 1);
sum -= path.getLast();
path.removeLast();
}
回溯的完整代码如下
class Solution {
List<List<Integer>> result = new ArrayList<>();
List<Integer> path = new ArrayList<>();
int sum = 0;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);//升序排列为了去重
backTracking(candidates, target, 0);
return result;
}
private void backTracking(int[] candidates, int target, int startIndex){
if(sum == target){
result.add(new ArrayList<>(path));
}
for(int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){
if(i > startIndex && candidates[i] == candidates[i - 1])continue;
sum += candidates[i];
path.add(candidates[i]);
backTracking(candidates, target, i + 1);
sum -= path.getLast();
path.removeLast();
}
}
}
分割回文串
这道题就是给一个字符串,然后要把这个字符串分割成一些回文子串,返回所有分割方案,每个分割方案就是一个组合
我们来梳理一下思路
- 逐步从字符串中切割子串,检查子串是否为回文。如果是回文,则将子串加入当前分割路径🤔 在递归过程中,可以使用双指针或预先使用动态规划表来判断子串是否为回文,这里我们先使用双指针来判断回文🤔 当递归到字符串末尾时,当前分割路径即为一个有效的回文分割,将其加入结果集🤔 在递归返回时,移除最后一个加入的子串,尝试不同的分割方案🤔
我们来进一步梳理回溯三要素
- 确定递归的参数和返回值
List<List<String>> result = new ArrayList<>();
List<String> path = new ArrayList<>();
private void backtracking(String s, int startIndex){}
- 回溯终止条件(当搜索的数字索引到字符串的尾部则将分割的方案加入结果集中)
if(startIndex == s.length()){
result.add(new ArrayList<>(path));
return;
}
- 单层搜索过程
for(int i = startIndex; i < s.length(); i++){
String subStr = s.substring(startIndex, i + 1);//切割子串
if(check(subStr)){
path.add(subStr);//切割的是回文子串则加入组合方案中
backtracking(s, i + 1);//递归继续尝试分割剩余字符串
path.removeLast();//回溯
}
}
完整的回溯代码如下
class Solution {
List<List<String>> result = new ArrayList<>();
List<String> path = new ArrayList<>();
public List<List<String>> partition(String s) {
backtracking(s, 0);
return result;
}
private void backtracking(String s, int startIndex){
if(startIndex == s.length()){
result.add(new ArrayList<>(path));
return;
}
for(int i = startIndex; i < s.length(); i++){
String subStr = s.substring(startIndex, i + 1);
if(check(subStr)){
path.add(subStr);
backtracking(s, i + 1);
path.removeLast();
}
}
}
private boolean check(String str){
int len = str.length();
for(int i = 0; i < len / 2; i++){
if(str.charAt(i) != str.charAt(len - 1 - i)) return false;
}
return true;
}
}
总结
又是学习回溯的新一天,继续加油✊✊✊