2-1众数问题
(一)题目
问题描述
给定含有 n n n个元素的多重集合 S S S,每个元素在 S S S中出现的次数称为该元素的重数。多重集 S S S中重数最大的元素称为众数。例如: S = 1 , 2 , 2 , 3 , 5 S={1,2,2,3,5} S=1,2,2,3,5。多重集 S S S的众数是2,其重数为3。
算法设计
对于给定的由 n n n个自然数组成的多重集 S S S,计算 S S S的众数及其重数。
数据输入
输入数据由文件名为input.txt的文本文件提供。文件的第一行为多重集 中元素个数 n n n,接下来的 n n n行中,每行有一个自然数。
结果输出
将计算结果输出到文件output.txt。输出文件有两行,第1行是众数,第2行是重数。
(二)解法
采用分治的思想,用递归实现,两种方法主要是排序与不排序的区别
方法1:分治递归(先经过排序)
算法思路
先把数组排序,对于一个排好序的长度为 n n n数组 a a a,我们可以通过中位数将数组分成3部分——中位数左边的部分、中位数、中位数右边的部分;
用两个指针 l l l和 r r r分别指向中位数第一次出现的位置和最后一次出现的下一个位置, r − l r-l r−l即为该中位数的重数 c n t cnt cnt,如果 c n t cnt cnt大于当前最大的重数 m a x c n t maxcnt maxcnt,我们就将该中位数更新为众数, c n t cnt cnt更新为 m a x c n t maxcnt maxcnt;
如果中位数左边部分的长度大于 m a x c n t maxcnt maxcnt,说明该部分可能存在众数,将其递归;
如果中位数右边部分的长度大于 m a x c n t maxcnt maxcnt,说明该部分可能存在众数,将其递归;
当递归不再进行时,说明整个数组的众数已找到。
举例
源代码
#include<iostream>
#include<cstdio>
#include<fstream>
#include<algorithm>
using namespace std;
//数组长度
int n;
//数组
int a[1000];
//众数的下标
int num;
//重数的重数
int maxcnt;
//读取
void read();
//写入
void write();
//将长度为n的一段数组分为中位数左边的部分、中位数、中位数右边的部分
void split(int a[], int n, int &l, int &r);
//求众数及其重数
void findMaxCnt(int &num, int &maxcnt, int a[], int n);
int main()
{
//读取
read();
//对数组排序
sort(a, a + n);
//求众数及其重数
findMaxCnt(num, maxcnt, a, n);
//写入
write();
return 0;
}
void read()
{
ifstream ifs;
//打开输入文件
ifs.open("G:\\algorithm\\data\\2_1_in.txt", ios::in);
//读取数据
ifs>>n;
for (int i = 0; i < n; ++i)
{
ifs>>a[i];
}
//关闭输入文件
ifs.close();
}
void write()
{
ofstream ofs;
//创建输出文件
ofs.open("G:\\algorithm\\data\\2_1_1out.txt", ios::out);
//写入数据
ofs<<a[num]<<endl;
ofs<<maxcnt<<endl;
//关闭输出文件
ofs.close();
}
void split(int a[], int n, int &l, int &r)
{
int mid = n / 2;
for (l = 0; l < n; ++l)
{
if (a[l] == a[mid])
{
//此时l为中位数第一次出现的位置
break;
}
}
for (r = l + 1; r < n; ++r)
{
if (a[r] != a[mid])
{
//此时r为中位数最后一次出现的下一个位置
break;
}
}
}
void findMaxCnt(int &num, int &maxcnt, int a[], int n)
{
int l, r;
//将长度为n的一段数组分为中位数左边的部分、中位数、中位数右边的部分
split(a, n, l, r);
//此时的中位数
int mid = n / 2;
//此时中位数的重数
int cnt = r - l;
//若该中位数的重数大于最大的重数,将该中位数更新为众数,该中位数的重数更新为最大重数
if (cnt > maxcnt)
{
maxcnt = cnt;
num = mid;
}
//如果中位数左边的元素个数大于最大的重数,则继续递归
if (l > maxcnt)
{
findMaxCnt(num, maxcnt, a, l);
}
//如果中位数右边的元素个数大于最大的重数,则继续递归
if (n - r > maxcnt)
{
findMaxCnt(num, maxcnt, a + r, n - r);
}
}
方法2:分治递归(不经过排序)
算法思路
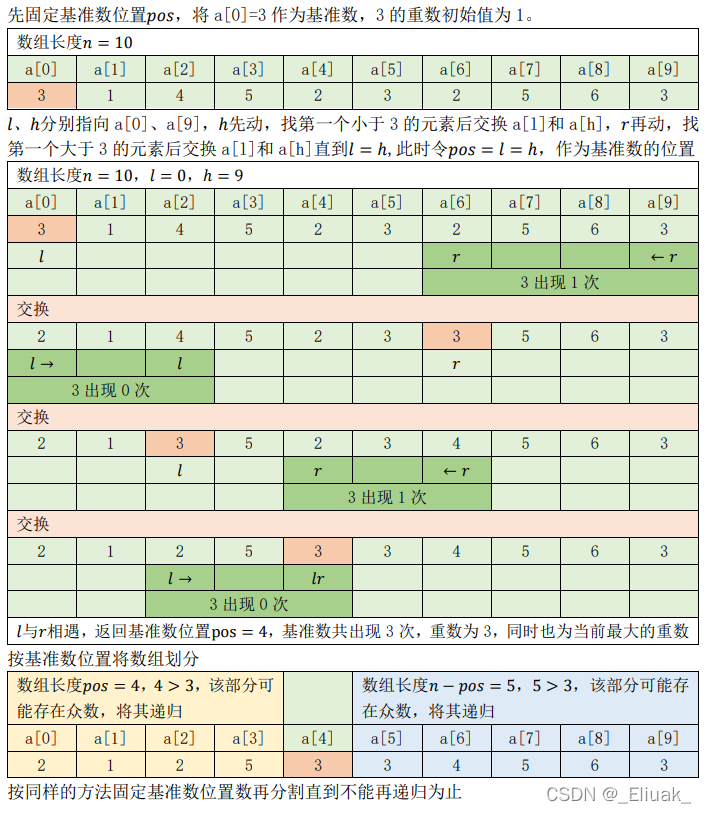
对于一个无序的数组 a a a,参考快速排序确定基准数位置的方法,我们可以在一趟排序中把小于等于基准数的数放在基准数左边,把大于等于基准数的数放在基准数右边,同时记录下基准数出现的次数 c n t cnt cnt,如果 c n t cnt cnt大于当前最大的重数 m a x c n t maxcnt maxcnt,我们就将该基准数更新为众数, c n t cnt cnt更新为 m a x c n t maxcnt maxcnt;
如果小于等于基准数的部分长度大于 m a x c n t maxcnt maxcnt,说明该部分可能存在众数,将其递归;
如果大于等于基准数的部分长度大于 m a x c n t maxcnt maxcnt,说明该部分可能存在众数,将其递归;
当递归不再进行时,说明整个数组的众数已找到。
举例
源代码
#include<iostream>
#include<cstdio>
#include<fstream>
#include<algorithm>
using namespace std;
//数组长度
int n;
//数组
int a[1000];
//众数的下标
int num;
//重数的重数
int maxcnt;
//读取
void read();
//写入
void write();
//交换数组中的两个元素
void swap(int a[], int i, int j);
//将一段数组分为小于等于基准数的部分、基准数(只有一个)、大于基准数的部分
int partition(int a[], int l, int h, int &cnt);
//求众数及其重数
void findMaxCnt(int &num, int &maxcnt, int a[], int l, int h);
int main()
{
//读取
read();
//求众数及其重数
findMaxCnt(num, maxcnt, a, 0, n - 1);
//写入
write();
return 0;
}
void read()
{
ifstream ifs;
//打开输入文件
ifs.open("G:\\algorithm\\data\\2_1_in.txt", ios::in);
//读取数据
ifs>>n;
for (int i = 0; i < n; ++i)
{
ifs>>a[i];
}
//关闭输入文件
ifs.close();
}
void write()
{
ofstream ofs;
//创建输出文件
ofs.open("G:\\algorithm\\data\\2_1_2out.txt", ios::out);
//写入数据
ofs<<a[num]<<endl;
ofs<<maxcnt<<endl;
//关闭输出文件
ofs.close();
}
void swap(int a[], int i, int j)
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
int partition(int a[], int l, int h, int &cnt)
{
//假设基准数pivot为数组的第一个元素
int pivot = a[l];
//povit出现一次
cnt = 1;
while (l < h)
{
//h指针左移找到第一个小于povit的数,交换l、h指针所指的值
while (l < h && a[h] >= pivot)
{
if (a[h] == pivot)
{
cnt++;
}
h--;
}
swap(a, l, h);
//l指针右移找到第一个大于povit的数,交换l、h指针所指的值
while (l < h && a[l] <= pivot)
{
if (a[l] == pivot)
{
cnt++;
}
l++;
}
swap(a, l, h);
}
//返回基准数的位置,此时l=h
return l;
}
void findMaxCnt(int &num, int &maxcnt, int a[], int l, int h)
{
//基准数的重数
int cnt;
//将一段数组分为小于等于基准数的部分、基准数(只有一个)、大于基准数的部分
int pos = partition(a, l, h, cnt);
//若该基准数的重数大于最大的重数,将该基准数数更新为众数,该基准数数的重数更新为最大重数
if (cnt > maxcnt)
{
maxcnt = cnt;
num = pos;
}
//如果基准数左边的元素个数大于最大的重数,则继续递归
if (pos > maxcnt)
{
findMaxCnt(num, maxcnt, a, 0, pos - 1);
}
//如果基准数右边的元素个数大于最大的重数,则继续递归
if (n - pos > maxcnt)
{
findMaxCnt(num, maxcnt, a, pos + 1, n - 1);
}
}
结果示例
输入:
输出:
(三)总结
两种方法本质上差别不大,时间复杂度也相同
方法1:分治递归(先经过排序)
时间复杂度
read()函数的时间复杂度为 O ( n ) \Omicron(n) O(n)
write()函数的时间复杂度为 O ( 1 ) \Omicron(1) O(1)
sort()函数的时间复杂度为 O ( n l o g n ) \Omicron(nlogn) O(nlogn) (sort函数结合了快速排序-插入排序-堆排序 三种排序算法)
split()函数的时间复杂度为 O ( n ) \Omicron(n) O(n)
findMaxCnt()函数的时间复杂度递推式为:
T
1
(
n
)
=
{
O
(
1
)
,
n
=
1
2
T
1
(
n
2
)
+
O
(
n
)
,
n
>
1
T1(n)=\begin{cases} \Omicron(1),\;\qquad\;\;\ \qquad \quad \qquad n=1\\ 2T1(\frac{n}{2})+\Omicron(n),\;\;\quad\qquad n>1\\ \end{cases}
T1(n)={O(1), n=12T1(2n)+O(n),n>1
因此,
T
1
(
n
)
=
2
T
1
(
n
2
)
+
n
O
(
1
)
=
2
(
2
T
1
(
n
2
2
)
+
n
2
O
(
1
)
)
+
n
O
(
1
)
=
2
2
T
1
(
n
2
2
)
+
2
⋅
n
O
(
1
)
=
.
.
.
=
n
T
1
(
1
)
+
l
o
g
n
⋅
n
O
(
1
)
=
O
(
n
l
o
g
n
)
\begin{aligned}T1(n)&=2T1(\frac{n}{2})+n\Omicron(1)\\&=2(2T1(\frac{n}{2^2})+\frac{n}{2}\Omicron(1))+n\Omicron(1)\\&=2^2T1(\frac{n}{2^2})+2\cdot n\Omicron(1)\\&=...\\&=nT1(1)+logn\cdot n\Omicron(1)\\&=\Omicron(nlogn)\end{aligned}
T1(n)=2T1(2n)+nO(1)=2(2T1(22n)+2nO(1))+nO(1)=22T1(22n)+2⋅nO(1)=...=nT1(1)+logn⋅nO(1)=O(nlogn)
整个算法的时间复杂度为:
T
(
n
)
=
O
(
n
)
+
O
(
n
l
o
g
n
)
+
T
1
(
n
)
+
O
(
1
)
=
O
(
n
l
o
g
n
)
\begin{aligned}T(n)&=\Omicron(n)+\Omicron(nlogn)+T1(n)+\Omicron(1)\\&=\Omicron(nlogn)\end{aligned}
T(n)=O(n)+O(nlogn)+T1(n)+O(1)=O(nlogn)
方法2:分治递归(不经过排序)
时间复杂度
read()函数的时间复杂度为 O ( n ) \Omicron(n) O(n)
write()函数的时间复杂度为 O ( 1 ) \Omicron(1) O(1)
swap()函数的时间复杂度为 O ( 1 ) \Omicron(1) O(1)
partition()函数的时间复杂度为 O ( n ) \Omicron(n) O(n) (每个元素要遍历一次)
findMaxCnt()函数的时间复杂度递推式为:
T
1
(
n
)
=
{
O
(
1
)
,
n
=
1
2
T
1
(
n
2
)
+
O
(
n
)
,
n
>
1
T1(n)=\begin{cases} \Omicron(1),\;\qquad\;\;\ \qquad \quad \qquad n=1\\ 2T1(\frac{n}{2})+\Omicron(n),\;\;\quad\qquad n>1\\ \end{cases}
T1(n)={O(1), n=12T1(2n)+O(n),n>1
因此,
T
1
(
n
)
=
2
T
1
(
n
2
)
+
n
O
(
1
)
=
2
(
2
T
1
(
n
2
2
)
+
n
2
O
(
1
)
)
+
n
O
(
1
)
=
2
2
T
1
(
n
2
2
)
+
2
⋅
n
O
(
1
)
=
.
.
.
=
n
T
1
(
1
)
+
l
o
g
n
⋅
n
O
(
1
)
=
O
(
n
l
o
g
n
)
\begin{aligned}T1(n)&=2T1(\frac{n}{2})+n\Omicron(1)\\&=2(2T1(\frac{n}{2^2})+\frac{n}{2}\Omicron(1))+n\Omicron(1)\\&=2^2T1(\frac{n}{2^2})+2\cdot n\Omicron(1)\\&=...\\&=nT1(1)+logn\cdot n\Omicron(1)\\&=\Omicron(nlogn)\end{aligned}
T1(n)=2T1(2n)+nO(1)=2(2T1(22n)+2nO(1))+nO(1)=22T1(22n)+2⋅nO(1)=...=nT1(1)+logn⋅nO(1)=O(nlogn)
整个算法的时间复杂度为:
T
(
n
)
=
O
(
n
)
+
O
(
n
l
o
g
n
)
+
T
1
(
n
)
+
O
(
1
)
=
O
(
n
l
o
g
n
)
\begin{aligned}T(n)&=\Omicron(n)+\Omicron(nlogn)+T1(n)+\Omicron(1)\\&=\Omicron(nlogn)\end{aligned}
T(n)=O(n)+O(nlogn)+T1(n)+O(1)=O(nlogn)