目录
什么是动态规划
概念
- 动态规划(Dynamic Programming,DP):用来解决最优化问题的算法思想。
- 一般来说,动态规划将复杂的问题分解为若干子问题,通过综合子问题的最优解来得到原问题的最优解。
- 动态规划会将每个求解过的子问题记录下来,这样下次碰到相同的子问题,就可以直接使用之前记录的结果,而不重复计算。
动态规划的特点
- 最优子结构:动态规划将一个复杂的问题分解成若干个子问题,通过综合子问题的最优解来得到原问题的最优解。(“分”与“合”体现在 状态转移方程)其实有时候用动态规划也不一定就是最优解那种意思。比如斐波拉契数列,我们很难从中体会到最优解的意味。我感觉这句话是在告诉我们:出现最优解的问题的时候,要第一时间想到动态规划,不是最优解的问题时,也要想到动态规划分解子问题的思想!
- 重叠子问题:动态规划会将每个求解过的子问题的解记录下来,这样当下一次碰到同样的子问题时,就可以直接使用之前记录的结果,而不是重复计算。(虽然动态规划使用这种方式来提高计算效率,但不能说这种做法就是动态规划的核心)所谓 记录就是dp数组。
动态规划的写法
- 递归,自顶向下(Top-down Approach),即从目标问题开始,将它分解成子问题的组合,直到分解至边界为至。
- 递推,自底向上(Bottom-up Approach),即从边界开始,不断向上解决问题,直到解决了目标问题;
适用的场景
- 适用场景:最大值/最小值, 可不可行, 是不是,方案个数
何时使用动态规划
- 一个问题必须拥有重叠子问题和最优子结构,才能使用动态规划去解决。
- 为什么呢?就像我们要求一个学校的考试最高分,那么我们可以从把人分为一个个班级,全校的最高分肯定是班级的最高分,我们要求全校的最高分,要从一个个班级中的最高分去选择
核心套路
- 其核心就是写出其状态转移方程(穷举)
因为状态转移方程体现了动态规划重叠子问题和最优子结构这两个特性,因此书写状态转移方程是最困难的。下面是从网上学到的一个思维框架,用于辅助思考状态转移方程:
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义。
# 初始化 base case dp[0][0][...] = base # 进行状态转移 for 状态1 in 状态1的所有取值: for 状态2 in 状态2的所有取值: for ... dp[状态1][状态2][...] = 求最值(选择1,选择2...)区别
分治和动态规划
- 共同点:都是将问题分解成子问题,然后合并子问题的解得到原问题。
- 区别:分治分出来的子问题是不重叠的,如归并排序和快速排序(分别处理左右排序,然后将左右序列结果合并),分治解决的问题不一定是最优化问题。动态规划解决的问题拥有重叠子问题,且一定是最优化问题。
贪心和动态规划
- 共同点:都要求问题拥有最优子结构。
- 贪心:整个过程以单链的流水方式进行,显然这种“最优的选择”的正确性需要用归纳法证明。例如数塔问题,贪心从最上层开始,每次选择左下或右下较大的那个,一直到最底层得到结果,显然这不一定可以得到最优解。
- 动态规划:无论采用自底向上还是自顶向下的方法,都是从边界向上得到最优解,它总是会考虑所有子问题,并选择继承能得到最优结果那个,对于暂时没被继承的子问题,由于重叠子问题的存在,后期可能会再次考虑它,因此还有机会成为全局最优的一部分,不需要放弃。
斐波那契理解动态规划
暴力递归(全部枚举)
- 发现有大量的重复计算
- 其实斐波那契不算一个动态规划,只是帮助我们理解动态规划
斐波那契数列记忆化搜索(递归写法)
- 去除了重复计算,剪枝
- 这种还是自上而下
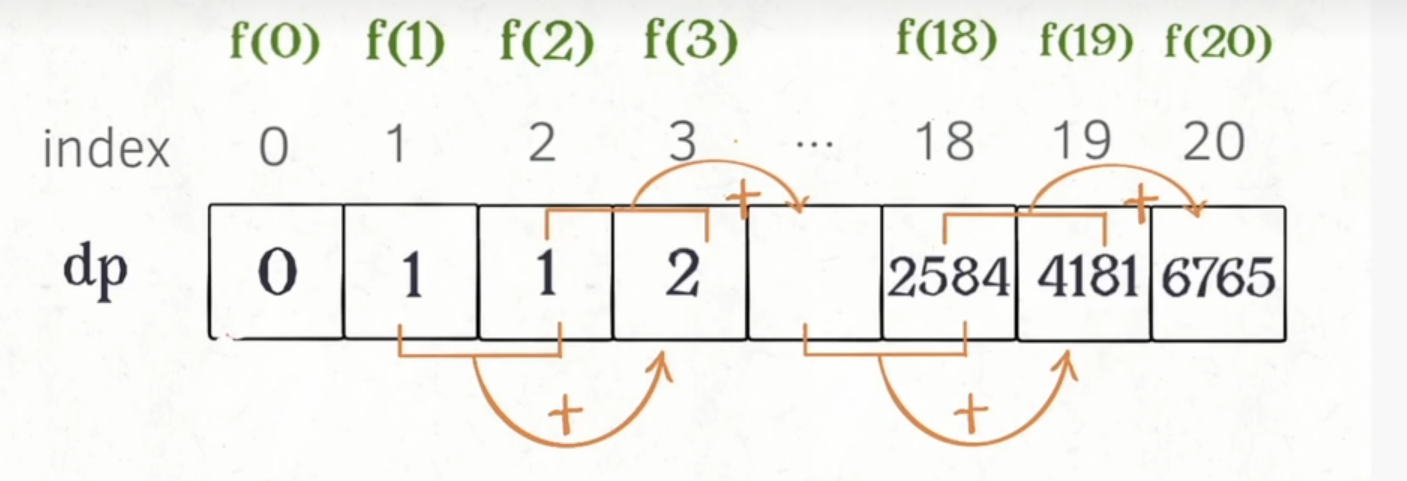
斐波那契数列递推写法
换零钱问题
- 这样写还是存在大量的重复计算,两种解决方法,剪枝和自底向上
- 这是自顶向下的剪枝写法
自底向上
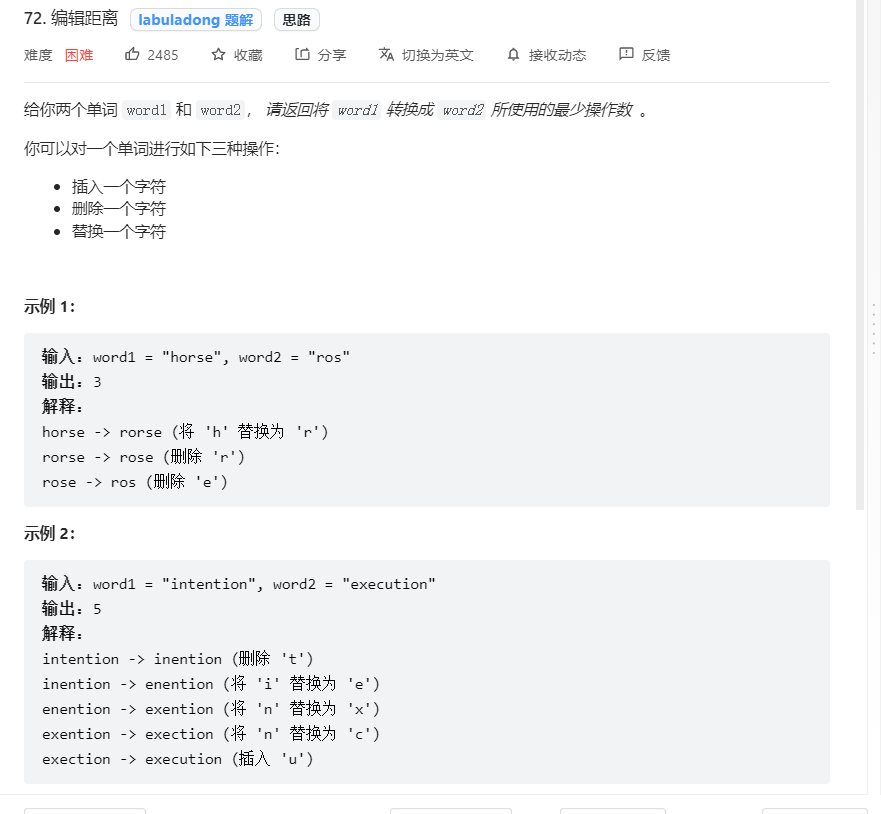
编辑距离问题
这道题首先我们要知道我们讲一个字符串变成另一个字符串的基本流程
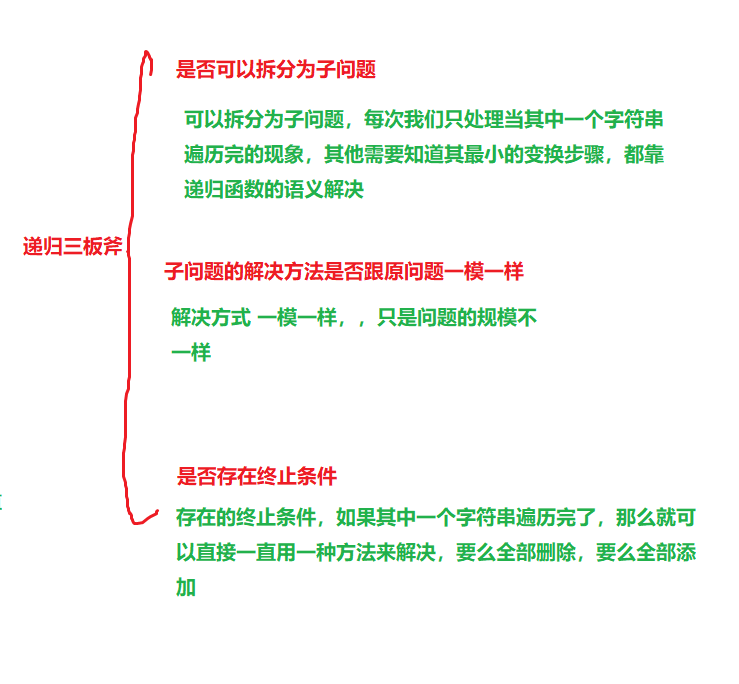
- 我们发现不止三种操作,还有一种就是如果匹配上了,那么我们就不需要对这个两个字符处理,直接去比较前面的字符串
- 当我们发现有一个字符串的指针已经走完了,但是另一个没有走完,如果是要修改的字符串没有走完,那就是将没有走完的字符全部删除,如果是将要变成的字符串没有走完,那么就是将其没走完的字符全部插入到要修改的字符串
知道了修改字符串的基本流程,我们可以写出暴力枚举的方法
class Solution { public int minDistance(String word1, String word2) { int n=word1.length(); int m=word2.length(); //n和m表示初始化指向字符串的最后一个索引 int min=helper(word1,n-1,word2,m-1); //helper函数的语义就是得到将word1变为word2的最短步数 //确定终止条件,当m==-1,说明word1走完 n==-1,说明word2走完 return min; } private int helper(String word1, int n, String word2, int m) { if(n==-1){ //说明word1已经走完了,需要将word2剩余的字符全部插入到word1 return m+1; } if (m==-1){ //说明 word2已经走完了,需要将word1中剩余没有遍历的字符全部删除 return n+1; } if(word1.charAt(n)==word2.charAt(m)){ //说明两个字符是一样的,不需要处理 //直接去处理前面的字符串 且需要处理的步数是跟前面的子字符串是一样的 return helper(word1,n-1,word2,m-1); } //走到这,说明这两个对应的字符串必须要处理,去递归找到操作数最少的一个方法 return Math.min( helper(word1,n,word2,m-1)+1,//做插入操作 Math.min(helper(word1,n-1,word2,m)+1,做删除操作 helper(word1,n-1,word2,m-1)+1));//做替换操作); } }优化
为什么知道要优化
- 因为存在重叠子问题,就肯定存在大量的重复计算,因为我们想从[i][j]走到[i-1][j-1]存在两条路径,一个是直接通过替换走到[i-1][j-1],或者通过插入先走到[i][j-1],然后通过删除走到[i-1][j-1]
- 有重叠子问题的存在,我们要么使用记忆化搜索,要么自底向上进行动态规划
剪枝
class Solution { public int minDistance(String word1, String word2) { int n=word1.length(); int m=word2.length(); //备忘录 int dp[][]=new int[n][m]; for (int []row:dp) { Arrays.fill(row,-1); } //n和m表示初始化指向字符串的最后一个索引 int min=helper(word1,n-1,word2,m-1,dp); //helper函数的语义就是得到将word1变为word2的最短步数 //确定终止条件,当m==-1,说明word1走完 n==-1,说明word2走完 return min; } private int helper(String word1, int n, String word2, int m,int dp[][]) { if(n==-1){ //说明word1已经走完了,需要将word2剩余的字符全部插入到word1 return m+1; } if (m==-1){ //说明 word2已经走完了,需要将word1中剩余没有遍历的字符全部删除 return n+1; } if (dp[n][m]!=-1){ return dp[n][m]; } if(word1.charAt(n)==word2.charAt(m)){ //说明两个字符是一样的,不需要处理 //直接去处理前面的字符串 且需要处理的步数是跟前面的子字符串是一样的 dp[n][m]= helper(word1,n-1,word2,m-1,dp); return dp[n][m]; } //走到这,说明这两个对应的字符串必须要处理,去递归找到操作数最少的一个方法 dp[n][m]= Math.min( helper(word1,n,word2,m-1,dp)+1,//做插入操作 Math.min(helper(word1,n-1,word2,m,dp)+1,做删除操作 helper(word1,n-1,word2,m-1,dp)+1));//做替换操作); return dp[n][m]; } }自底向上动态规划
- 我们正常思路是将horse,一步步变成ros,是自顶向下的操作,而自底向上,是考虑从空字符串开始,比如从h到ros,从ho到ros,直到horse到ros
class Solution { public int minDistance(String word1, String word2) { int m=word1.length();//5 int n=word2.length();//3 int dp[][]=new int[n+1][m+1]; //base case for (int i = 0; i <=n ; i++) { dp[i][0]=i; } for (int i = 0; i <=m; i++) { dp[0][i]=i; } for (int i = 1; i <=n; i++) { for (int j = 1; j <=m; j++) { if(word1.charAt(j-1)==word2.charAt(i-1)){ dp[i][j]=dp[i-1][j-1]; }else { dp[i][j]=Math.min(Math.min(dp[i-1][j-1]+1,dp[i-1][j]+1), dp[i][j-1]+1); } } } return dp[n][m]; } }